基于离散频率编码的PD雷达二维解模糊方法
孙希平, 卢景月, 张 磊,*, 钟卫军
(1. 中山大学电子与通信工程学院, 广东 广州 510006;2. 西安电子科技大学电子工程学院, 陕西 西安 710071;3. 西北工业大学自动化学院, 陕西 西安 710072)
0 引 言
雷达作为一种利用电磁波辐射的主动探测传感器,可以对超远距目标进行探测,这一特性决定了雷达成为战机上的关键设备,对于战机在战场上提前发现目标的能力至关重要。机载脉冲多普勒(pulse Doppler, PD)雷达的中脉冲重复频率(medium pulse repetition frequency, MPRF)波形具有全方位的探测能力[1],因此在机载火控中备受重视。但是MPRF对目标的探测可能同时存在距离和多普勒的二维模糊,需要对二维模糊进行正确处理以后,才能进行准确的目标参数提取以供战场态势评估。
就雷达工作原理来说,距离模糊的本质在于脉冲信号的周期性发射,多普勒模糊在于多普勒采样率的不足,因此两者是一对相互矛盾的量。对于距离模糊,可以使用距离搜索方法[2]、混合滤波[3]解模糊,或者使用脉冲间相位编码[4-5]、脉冲频率编码[6]等,对发射波形序列进行标记以解决距离模糊的问题。但是这种方法只能解决距离模糊。由于需要多个脉冲作为一组信号进行距离解模糊,等效脉冲重复频率降低,因此增加了多普勒的模糊。文献[7]中,提出一种使用正交频分复用(orthogonal frequency division multiplexing, OFDM)正交波形进行距离解模糊的方案,为了保证一定范围的多普勒测量,需要通过增加脉冲重复频率获得距离不模糊区域的扩展。多普勒模糊通常可以通过变脉冲重复频率[8]、结合测距信息[9]、利用信号多普勒敏感性[10]等方法解决。通过改变脉冲重复频率或者信号波长,可以改变目标速度对应的多普勒频率,通过多组信息的匹配可以对速度进行解模糊[8]。文献[10]提出了一种利用信号多普勒敏感性解多普勒模糊的方法,利用不同模糊数搜索时目标脉压结果的幅度,根据最大匹配滤波峰值确定多普勒模糊数,以此来解决多普勒模糊问题。经典的多脉冲重复频率(multiple pulse repetition frequency, Multi-PRF)方法是一种有效的距离-多普勒二维解模糊方法[11-13]。Multi-PRF在被提出后,已经广泛应用在MPRF模式的信号处理中,并且演变出了多个形式。在Multi-PRF模式下,利用中国余数定理[11-12]或者距离-多普勒扩展聚类[13]的方法,可以对目标距离和多普勒进行同时解模糊。但是在各脉冲重复频率(pulse repetition frequency, PRF)探测结果匹配过程中,容易产生虚假目标。且为了准确匹配,需要目标在驻留时间内不发生越距离单元运动,对高速目标进行探测时需要限制每个PRF脉冲簇的脉冲个数,造成积累信噪比增益有限,在低信噪比情况下,可能无法有效检测目标,造成漏警。
本文针对机载火控雷达MPRF下的二维(距离-多普勒)模糊问题以及传统方法无法长时间相参积累等缺点,提出了一种基于循环发射正交离散频率编码波形进行二维解模糊的方法,通过发射正交波形,不同距离模糊区域的回波对应不同的频率编码波形,使用由发射波形设计的匹配滤波器组可以进行不同距离模糊区域的分离,并且高速目标在较长时间的回波中,不可避免地产生距离走动,为了进行相参积累,利用Keystone进行距离走动校正。但是当回波存在多普勒模糊时,Keystone无法拉直回波包络,导致相参处理积累增益降低,因此可以搜索最佳相参积累增益下的补偿多普勒模糊数[14-15],确定回波的多普勒模糊次数,实现固定重频下的多普勒解模糊。对距离走动校正后,目标处于相同的距离单元,可以进行驻留时间内所有回波的相参积累,获得较高的相参处理增益,增加了在低信噪比回波情况下的检测及参数估计性能。
DFC波形与相位编码波形类似,具有图钉型的模糊函数[16-17],存在多普勒敏感性,在对信号的匹配滤波中,如果回波信号的多普勒频移较大,则会严重影响信号的脉压结果。本文针对回波信号存在的多普勒敏感性,将匹配滤波过程放在多普勒域内进行,对多普勒域内的每条多普勒谱线设计针对性的匹配滤波函数,不同多普勒的目标回波使用对应脉内的多普勒匹配滤波器,实现精确地匹配滤波,避免了由多普勒敏感性引起的匹配滤波增益降低或虚假目标产生,保证对不同速度目标的检测能力。
1 机载PD雷达回波模型
1.1 机载PD雷达的MPRF回波模型
机载火控PD雷达的MPRF情况下,多个位于不同距离模糊区域目标的回波模型如图1所示。假设雷达发射脉冲重复频率为Tr,其最大不模糊距离为Rum=cTr/2,其中c为光速。当目标距离大于Rum时,脉冲信号的重复周期小于雷达回波到达时间,产生距离模糊。如图1所示,不同模糊区域的目标回波叠加在一起到达雷达接收机。

图1 MPRF模式下距离模糊模型Fig.1 Range ambiguity model of MPRF
假设雷达使用一组脉冲进行循环发射,脉组中第n个发射脉冲可以表示为
sn(t)=un(t)exp(j2πfct)
(1)
式中:t表示时间;fc为发射信号载频;un(t)为第n个发射脉冲的脉内调制项。
设雷达视场中存在一个距离模糊的目标,考虑在空空模式下,迎飞目标具有高相对速度,雷达发射第n个脉冲时接收到的目标回波可以表示为
(2)
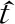
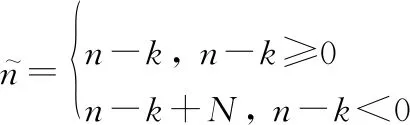
(3)
式中:k为目标的距离模糊次数,k满足
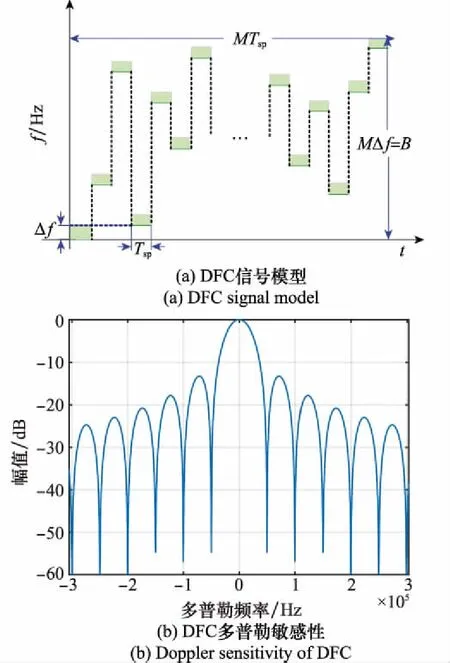
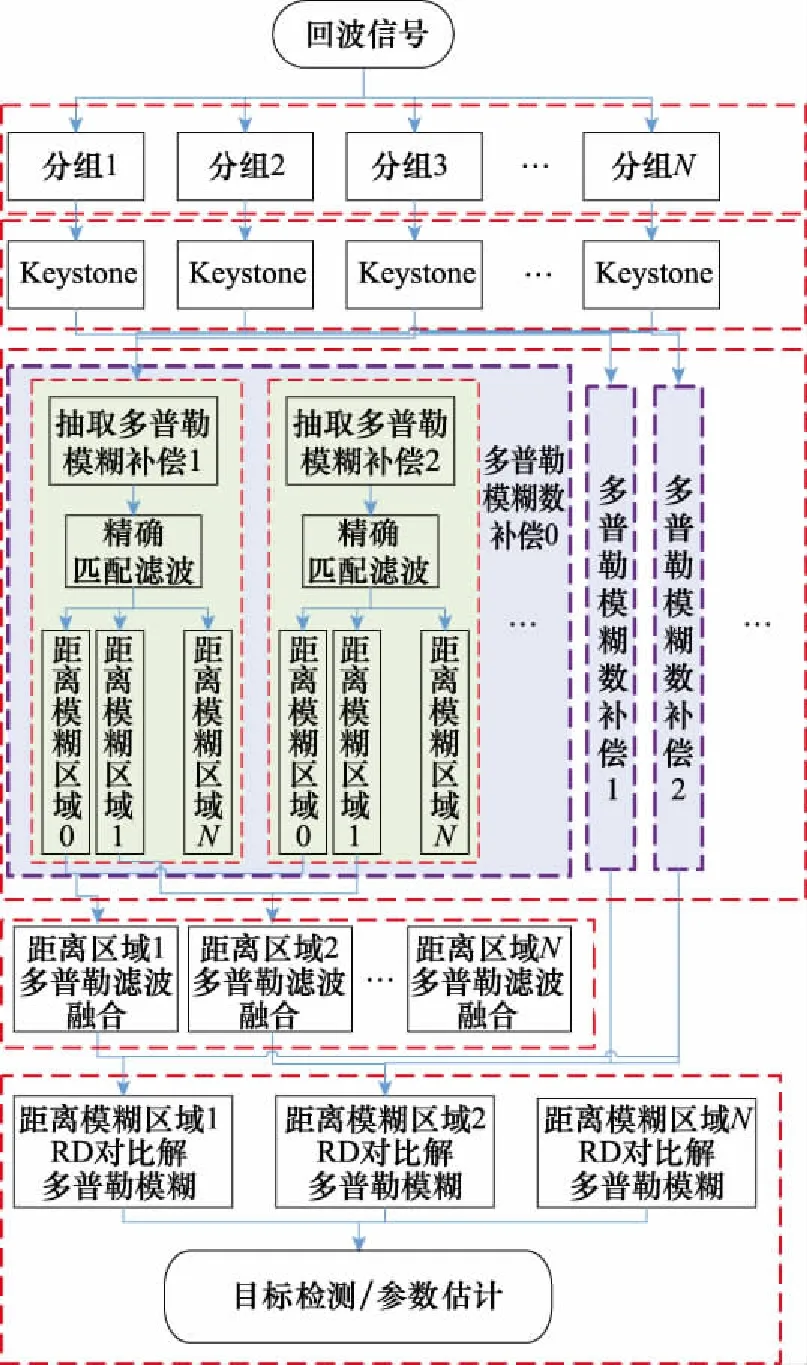
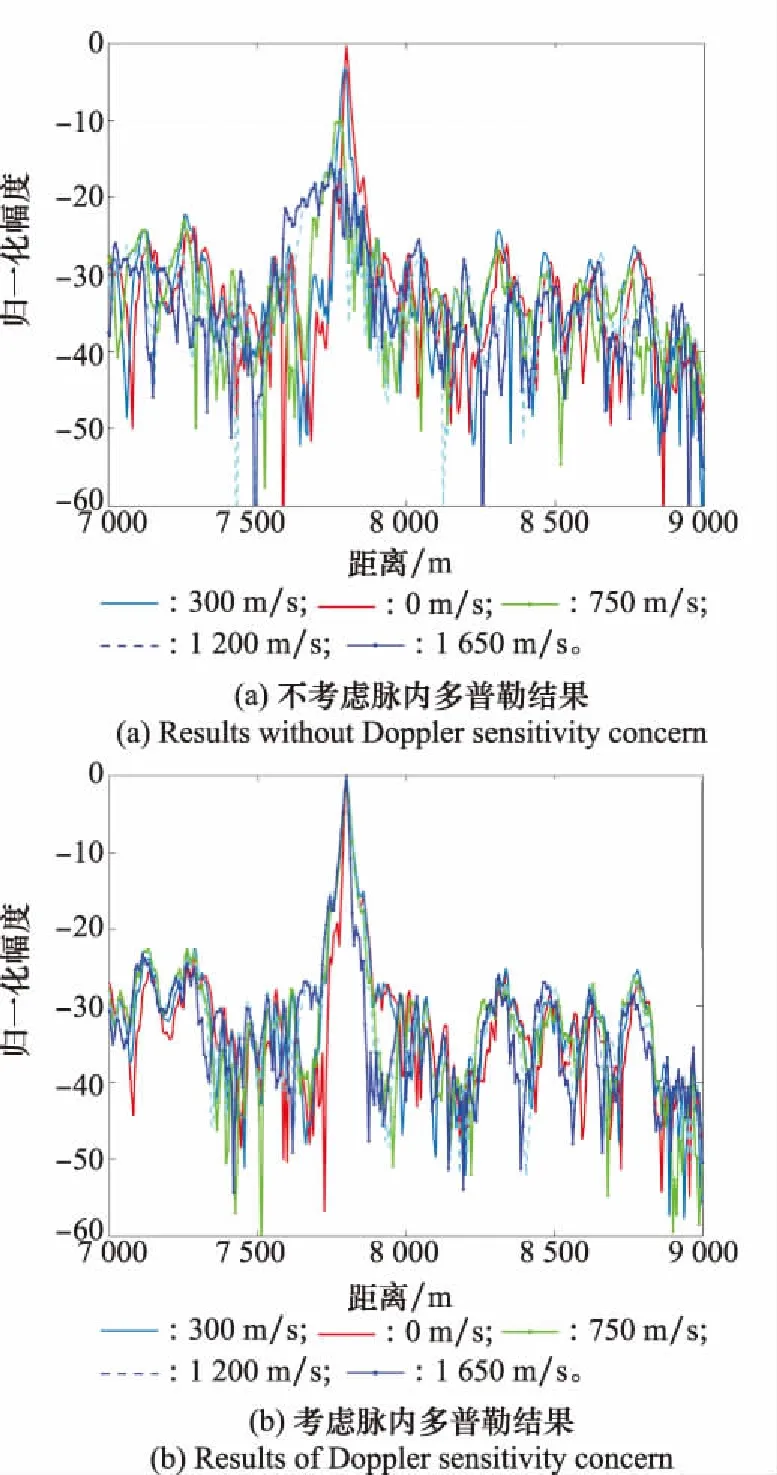
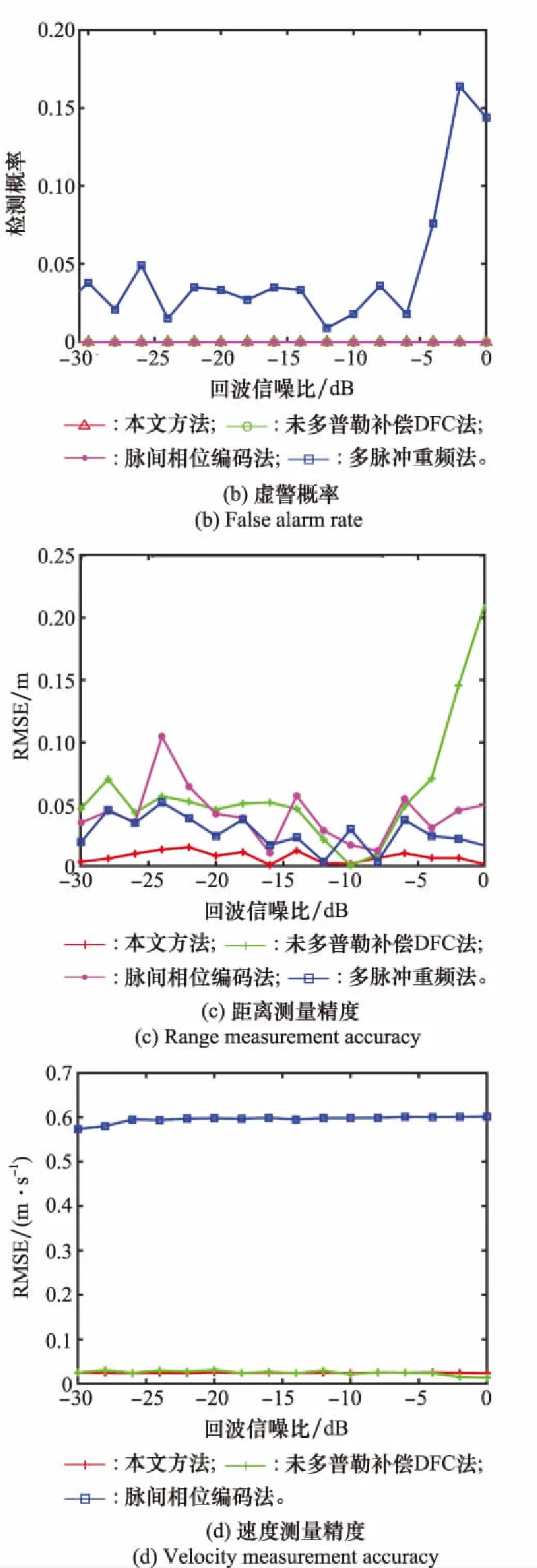
Rumk (4) 式中:R=R0+vtm表示目标的距离,R0为观测起始时间的目标距离,v为目标速度。 式(2)中,τ(tm)为目标在tm时刻的时延,考虑光速远大于目标速度,该时延可以表示为 (5) 目标回波信号被接收后,使用载频fc下变频至基频信号,基频信号可以表示为 (6) (7) 脉内多普勒会影响脉冲脉内调制项的快时间频域,在匹配滤波过程产生失配。 如上所述,在机载火控雷达中,距离-多普勒二维模糊必须得到解决,且在空空迎飞情况下,还需要考虑脉内多普勒调制问题。 雷达使用正交离散频率编码(discrete frequency coding, DFC)波形在空域探测目标,循环发射N个脉冲信号,每个发射脉冲具有不同的频率编码,N个脉冲信号构成一个脉组,在图1中展示了使用5个不同频率编码脉冲组成的一个发射脉组。图2(a)为一个典型DFC波形的示意图,发射脉冲由一系列点频窄脉冲信号随机排列拼接组成,每一个点频信号称为一个码片。式(1)中信号的脉内调制项可以表示为 图2 离散频率编码波形Fig.2 Discrete frequency coding waveform (8) 式中:rect(·)表示矩形函数;M为一个脉冲内的频率码片个数;Tsp为每个频率码片的时间宽度,整个脉冲时间宽度为MTsp;发射脉冲的频率编码序列为fn=anΔf,n表示脉冲在脉组中的索引,Δf为频率码片的频率间隔,且Δf=1/Tsp,an={a1,a2,…,aM}n为第n个脉冲频率编码系数,且是由整数{0,1,…,M-1}的乱序重排;un(t)表示第n个发射信号的脉内调制项。 文献[16]通过改变信号频率编码获得相互正交的DFC信号组。本文通过设定N个不同的频率编码,生成一组正交的DFC波形,并使用该信号组进行循环发射。在雷达的每次回波中,包含了与目标模糊区域对应的频率编码信号回波,对接收到的回波信号使用各个正交波形依次进行匹配滤波,可以准确地对不同距离模糊区域的回波进行分离。 频率编码信号具有与相位编码信号类似的图钉型模糊函数[17],这意味着高速目标回波的脉内多普勒调制项不可忽略,由于脉内多普勒的存在,使用发射信号设计的匹配滤波函数会引起失配,使得匹配滤波输出峰值降低,脉冲压缩增益损失。脉压增益的损失可以使用模糊函数0时延(脉压峰值)切片的多普勒响应进行评估,脉压峰值的多普勒响应可以表示为 (9) 式中:fd为信号的脉内多普勒频率;u*(t)表示共扼。将un(t)代入式(9)可得 R(fd)=MTspsinc(fdMTsp) (10) 图2(b)为一个码片数为20,码片时宽为1 μs的频率编码信号0时间延时切片相关结果的多普勒响应。由式(10)及图2(b)可知,随着脉内多普勒频率的增大,在回波信号使用发射信号作为匹配滤波参考函数时,脉冲压缩的峰值明显降低,其3 dB的增益损失对应的多普勒频率为22.3 kHz,当雷达波形载频为10 GHz时,对应的速度为334.5 m/s,在机载PD火控雷达中,当迎飞目标相对速度大于该速度时,脉冲压缩需要考虑脉内多普勒带来的影响。 本文根据DFC波形特性,提出了一种融合了精确匹配滤波的二维解模糊方法,本文不仅可以通过波形正交性以及Keystone多普勒模糊补偿准确解决距离-多普勒二维模糊,而且将回波信号的匹配滤波放在多普勒域进行,根据每条多普勒谱线进行针对性的匹配滤波器设计,消除空空模式可能存在的高速目标回波的PD对脉压的影响,从而达到最大化匹配滤波输出。本文算法流程图如图3所示,以下各小节将结合算法流程图对回波处理流程进行详细介绍。 图3 算法流程图Fig.3 Flow diagram of algorithm 考虑雷达对高速目标观测过程中,目标回波包络有越距离单元走动的现象,在进行相参积累时,会引起距离向以及多普勒向的主瓣展宽,无法获得最大的相参积累增益。本文使用Keystone方法,通过解决多普勒频域与距离频率的耦合关系,拉直信号包络,达到距离走动校正的目的,以获得较高的相参积累增益。且本文在多普勒域进行匹配滤波,因此Keystone是对脉压前的回波信号进行处理。 由于使用了一组正交DFC波形循环发射,因此在回波中同一目标相邻的回波在频域的调制项上并不一致,为了保证Keystone过程中信号慢时间重采样的正确性,需要对回波信号进行N次抽取,以保证Keystone在相邻脉冲之间有正确的插值信号,如图4(a)所示。 图4 信号抽取及多普勒模糊示意图Fig.4 Schematic diagram of signal extract and Doppler ambiguity 将脉内调制项un(t)进行傅里叶变换,第n个脉内调制信号对应的频域形式可以表示为 (11) 式中: (12) 根据式(6),目标基频回波的快时间频域为 (13) 对回波基频信号进行抽取,信号共分为N组,各个模糊区域的回波在相邻的脉冲间具有相同的频率编码,且不随慢时间变化。Keystone可以通过插值得到正确的慢时间重采样。由于信号抽取,各个脉组的起始距离会发生变化。设抽取后慢时间为tr=Ntm,第n个抽取分组表示为 (14) 对抽取后的脉冲分组在慢时间维度tr进行重采样,令τr=(f+fc)tr/fc,重采样后第n个脉冲分组的回波信号为 (15) 对于多普勒模糊的回波信号,由于式(15)中第二个指数项的存在,信号包络不完全处于同一个距离单元,需要进行补偿。进行准确的多普勒补偿后,信号包络才能处于同一距离单元,在相参积累后,获得最大的积累增益。利用这一特性,通过模糊数F1和F2的搜索遍历,根据相参积累最大积累增益对应的模糊数,达到多普勒解模糊的目的。多普勒模糊数补偿通过下式完成: (16) 式中:F=F1N+F2为对应的多普勒模糊数。通过遍历一定范围内的多普勒模糊数,并根据后续相参积累结果的峰值大小,可以找到对应的多普勒模糊数,完成多普勒解模糊。 由于DFC波形存在多普勒敏感性,本文将匹配滤波放在多普勒域进行,针对每一个多普勒谱线进行匹配滤波。在上一小节中,已经针对每组波形进行了速度模糊数估计,在不同的模糊数下,每条多普勒谱线对应不同的多普勒值。 对式(16)进行慢时间傅里叶变换,变换到快时间频率-多普勒域为 (17) 式中:TR表示回波的相干处理时间。 考虑多普勒模糊,上式可以重写为 (18) 式中:F为目标的多普勒模糊数, (19) (20) 此时,对回波信号快时间频域-多普勒域信号进行匹配滤波,同时得到距离解模糊结果。针对每一条多普勒谱线,设计匹配滤波器组: (21) 式中:r∈[1,2,…,N]表示不同的脉内调制项,对应于不同的距离模糊区域;(·)*表示取共轭,该匹配滤波器同时补偿了由抽取带来的起始距离的变化。 (22) 使用考虑了脉内多普勒的匹配滤波器组,将不同距离模糊区域的信号进行分离,并且该匹配滤波器与带有脉内多普勒调制的回波匹配,可以进行精确的匹配滤波。 进行精确匹配滤波后,补偿了脉内多普勒的影响,获得了每个抽取后脉组的距离-多普勒结果。为了获得更好的相参积累效果以及简化多普勒模糊数对比估计,对各个抽取后的脉冲分组结果进行融合,并在融合过程补偿掉由抽取带来的多普勒模糊问题,此时只需要估计目标多普勒相对于fp的多普勒模糊数。 由于发射脉冲是在固定重复频率下发射的,因此各个发射脉冲之间的时间间隔相同,在一个发射脉组内,多普勒采样是等间隔连续的,利用这一特性,可以进行多普勒滤波重构,如图5所示。利用多个抽取脉组的距离-多普勒结果,根据各个抽取脉组之间该多普勒频点之间的关系(式(22)最后一个相位项),重构出目标真实多普勒,解决由抽取带来的目标多普勒模糊。 图5 多普勒模糊及融合示意图Fig.5 Doppler ambiguity and fusion diagram A=[a-I,a-I+1,…,ai,…,aI-1,aI] (23) (24) (25) 令q为不同分组信号所具有的相同的距离像包络,p=[p-I,p-I+1,…,pF,…,pI-1,p-I],其中多普勒模糊数对应的pF为1,其他为0。 (26) 式(25)可以表示为 SB=(ApTq)T (27) (28) 式中:Wi为第i次多普勒模糊的权重系数,且Wi=A-1hT;h=[h-I,h-I+1,…,hi,…hI]为各个模糊分量的选择向量,令hi=1,其他为0。 将各个多普勒频点在不同多普勒模糊次数的结果,进行结果的拼接即可得到最终的融合后距离-多普勒结果: (29) 此步融合了整个抽取分组的能量,即不同距离模糊区域的多个分组也完成了相参积累,在此结果之上可以进行目标检测以及参数估计。 在经过以上步骤后,得到了回波在不同距离模糊区域以及不同多普勒模糊单元的距离-多普勒结果,对该结果进行二维恒虚警率(constant false-alarm rate, CFAR)检测[18]及参数估计。由于距离模糊根据信号正交性已经分离,此处检测结果的距离信息加上距离模糊区域对应的起始距离即为真实距离信息。对于多普勒模糊,当信噪比较高时,多普勒模糊数错误补偿的积累记过也会被检测出来,其多普勒中心与最优相参积累结果中心一致,利用不同多普勒模糊数补偿后的检测结果,对比不同模糊次数下多普勒频点的相参积累输出,找出最大值对应的多普勒模糊次数以及多普勒值,即可得到目标对应多普勒以及目标真实速度。对目标检测结果进行进一步处理,得到目标的参数估计结果进行输出。 为了便于衡量算法的工程实现可行性,对算法复杂度进行分析。假设一次处理内,共发射Na个脉组,共计NaN个脉冲,每个脉冲内的信号采样点为Nr,进行L次多普勒模糊遍历。在算法流程中,信号分组Keystone变换,算法运算量为NaNNr(1+log2Nr),多普勒模糊数补偿中,算法运算量为NrNaNL,脉冲压缩过程算法运算量为NrNaN2L(1+log2Nr),多普勒谱融合的运算量为NrNaNL,实际算法中,解速度模糊次数L与脉组脉冲个数相同,即L=N,算法流程的总运算量为 OP=NaNNr((1+N2)(1+log2Nr)+2N)≈NaNrN3log2Nr (30) 由式(30)可见,当脉组中脉冲个数N=1时,运算量最小为O(NaNrlog2Nr),随着N增大,运算量增大为O(NaNrN3log2Nr)。N增大不仅代表解距离模糊能力的提升,同时也增加了相参处理脉冲个数,提高多普勒分辨与测量能力。 为了证明利用循环发射DFC波形进行脉冲多普勒雷达在MPRF模式下对距离-多普勒二维解模糊以及低信噪比回波的目标检测能力,进行了以下两部分实验进行验证。① 使用正交性匹配滤波以及Keystone多普勒模糊校正,验证其可以准确解决距离-多普勒二维模糊;② 验证考虑多普勒敏感性的精确匹配滤波,应对不同速度目标的脉压结果输出、固定重频带来的整个驻留时间及长时间相参积累带来的信噪比增益,以及获得信噪比增益后目标检测和参数估计的优势。 在所进行的实验中,设定机载火控PD雷达循环发射5个正交DFC波形脉冲,可以进行最大4次的距离模糊分离。具体的雷达仿真参数如表1所示。按照信号正交性为优化目标函数,使用遗传算法进行频率编码的优化,得到发射的5个频率编码脉冲对应频率编码如表2所示。 表1 仿真参数 表2 频率编码 首先通过实验验证利用正交波形进行距离模糊区域区分的有效性,根据仿真参数,雷达的最大不模糊距离为15 km。在本实验中,设置3个分别位于不同距离模糊区域的目标,目标距离分别为7.8 km、27 km、33 km。由于对信号的匹配滤波在多普勒域中完成,因此需要对比相同多普勒目标的正交波形距离模糊区分结果,此处设定3个目标速度均为0。在一个波位驻留对应的相干处理时间内,共循环发射了256组信号,共1 280个脉冲。 图6为目标所在多普勒谱线的匹配滤波结果,由图中可以发现,对于在同一多普勒谱线的不同距离模糊区域目标,由于不同模糊区域具有对应的正交信号,只在相对应的距离模糊区域被正确的脉冲压缩,在其他区域由于匹配滤波器参考信号的正交,不产生峰值。图6(a)为距离不模糊区域的匹配滤波结果,信号输出主瓣附近为-32 dB左右的信号自相关旁瓣。位于目标距离模糊对应的区域,存在距离模糊区域回波信号与此区域编码信号的相关结果输出,由于信号的正交性,匹配滤波的峰值的主瓣旁瓣比大于22.87 dB,验证了发射波形的正交性,以及由正交性带来的距离模糊区域的区分。第3距离模糊区域无目标,对应的匹配滤波结果低于-22.55 dB,为信号旁瓣量级。 以上证明使用正交DFC波形可以实现在一定模糊旁瓣抑制的条件下,进行不同距离模糊区域的分离,接下来通过实验验证多普勒解模糊的有效性。 设定目标距离为7.8 km的目标速度为120 m/s,相对于最大不模糊速度来说,有了1次多普勒模糊,在回波信号进行Keystone模糊数搜索中,对不同模糊数下距离-多普勒结果中的值进行对比,结果如图7所示,进行多普勒模糊数为1的补偿后,相参积累结果具有高的峰值能量且主瓣较窄,其他模糊数补偿的相参积累结果由于目标距离像分布在多个距离单元,相参处理后能量未完全积累在同一个距离单元,峰值较低,且主瓣宽,影响距离分辨能力。表3为不同多普勒模糊数补偿下,积累峰值的输出。通过不同模糊数补偿的积累结果对比,可以确定回波信号的多普勒模糊数为1。目标在距离多普勒结果中,多普勒谱线对应的速度为-30.082 1 m/s,结合峰值比较输出得到的目标多普勒模糊数,以及1次多普勒模糊对应150 m/s,可以求得目标的估计速度为119.917 9 m/s,与设定目标基本一致。 图7 多普勒解模糊结果Fig.7 Result of doppler ambiguity resolution 表3 不同多普勒模糊数补偿的峰值 从能量以及DFC信号多普勒敏感性考虑出发,使用精确匹配滤波可以避免由匹配滤波函数不匹配引入的失配脉压增益损失。本节首先通过实验对比考虑脉内多普勒的匹配滤波与不考虑脉内多普勒的匹配滤波在不同速度目标下的匹配滤波输出。 为了验证不同脉内多普勒的影响,实验设置目标距离为7 800 m,目标速度范围为0~1 800 m/s,分别进行不同目标速度的回波仿真,在多普勒域根据每条多普勒谱线以及多普勒模糊次数,设计相应的匹配滤波器。为了进行对比,使用不考虑多普勒敏感性的匹配滤波对各多普勒单元进行匹配滤波,结果如图8(a)所示,从该结果可以明显看出,随着目标速度的增加,匹配滤波结果输出的主瓣峰值降低,旁瓣明显升高,同时速度越大,匹配滤波结果出现明显失真,无法获得匹配滤波增益,对目标的检测造成严重影响。图8(b)为不同速度下,使用本文方法的目标匹配滤波输出,由结果可见,匹配滤波结果的峰值没有明显展宽,匹配滤波输出的峰值基本保持不变,并且脉压输出的副瓣未产生明显升高。为了更加清晰地表示考虑多普勒敏感性匹配滤波的性能,如图8(c)和图8(d)所示,计算了两种匹配滤波方法在不同速度下的归一化峰值输出以及主瓣旁瓣比。如图8(c)所示,考虑了多普勒敏感性的匹配滤波输出主瓣峰值在不同速度下基本不变,但是不考虑多普勒敏感性的匹配滤波输出峰值随着速度升高持续下降,在1 500 m/s速度下、已经降低了13 dB,严重影响了目标的检测。如图8(d)所示,考虑了多普勒敏感性的匹配滤波输出的主副比,在1 500 m/s相对速度下依旧可以保持25 dB以上的主副比,而传统直接利用发射信号构造匹配滤波的结果,随着速度地增加,匹配滤波输出的主副比明显降低,在1 200 m/s的相对速度下主副比为8.76 dB,已经严重影响了匹配滤波的输出,极易造成目标的漏检或虚警。 图8 脉内多普勒对匹配滤波的影响Fig.8 Influence of Doppler sensitivity on matched filtering 为了验证本文所提算法对目标检测以及参数估计性能,与经典的多脉冲重频法[13]、脉冲间相位编码[5]以及DFC信号不考虑多普勒敏感性匹配滤波的方法进行对比。多脉冲重频法使用3/5原则,在一次驻留时间内,发射5组不同PRF的脉冲,具体PRF分别为15 kHz、8.7 kHz、7.2 kHz、11 kHz、13 kHz,每组PRF分别包含256个脉冲,信号带宽设置为与本文方法仿真一致。使用文献[5]文中13脉冲的方法进行对比,信号重频同样为10 kHz,信号带宽为20 MHz,每次驻留时间内共有100组脉冲簇。相对应的,在实验对比中,本文所提算法在每次驻留时间内进行256个脉组信号发射。用于对比的DFC信号不考虑多普勒敏感性匹配滤波方法,除了在匹配滤波不考虑脉内多普勒外,其他处理流程均与所提方法一致。 实验中,设置起始距离为7 800 m的目标速度为330 m/s,对仿真目标脉冲回波加入不同信噪比的高斯白噪声,通过150次蒙特卡罗实验进行目标检测以及测量精度实验。实验结果如图9所示,未多普勒补偿DFC法表示未考虑多普勒敏感性的DFC波形传统匹配滤波方法的结果。从图9(a)可以看到在每种信噪比下进行150次蒙特卡罗实验后不同算法的检测概率。多脉冲重频法和脉间相位编码法的结果分别在信噪比为-38 dB和-36 dB时,目标的检测概率已经趋近于0。对于未多普勒补偿DFC法,从图8(c)中可以看出,在目标速度为330 m/s时,由于匹配滤波的失配,脉压结果的峰值输出相对于考虑多普勒敏感性匹配滤波的结果下降了6 dB左右,峰值下降使得目标在回波信噪比为-40 dB时,只有24%左右的检测概率,在信噪比为-38 dB的情况下,检测概率为64%左右。由于本文方法在整个驻留时间的脉冲回波进行了相参积累,且考虑了脉内多普勒对脉压的影响,因此在回波信噪比为-44 dB的情况下,依旧有60%左右的检测概率。从结果可以看出,本文所提算法在低信噪比目标回波中的检测性能明显高于其他3种方法。低信噪比回波下的目标检测能力可以使雷达对相同距离目标探测时,在保持相同检测概率的情况下降低雷达发射功率,降低雷达信号被截获概率,增加雷达的射频隐身性能。由文献[13]可知,多脉冲重复频率方法在进行目标匹配时,容易产生虚假目标点,增大虚警率。图9(b)为不同信噪比下目标虚警率的对比结果,多脉冲重频法具有约5%的匹配虚假点,其他算法的目标检测虚警率接近0。本文所提处理方法有利于获得较高信噪比增益,使目标的测量结果更加精确。图9(c)为不同算法的目标距离测量精度,使用-30~0 dB的回波信噪比,以保证在各个算法对目标稳定检测下的测量精度的对比。从结果中可以看出,本文算法在不同信噪比下,目标距离测量精度可以保持在0.05 m以内,多脉冲重频法和脉间相位编码法方法的测量精度随着信噪比的提高也有提高,但是仍然大于本文所提方法。不考虑多普勒敏感性的DFC波形方法由于脉内多普勒引起目标主瓣展宽,使得目标距离分辨变差,且在CFAR固定检测门限下,在回波高信噪比情况下更容易检测到展宽的主瓣,使得目标的距离测量结果变差。对于目标速度的测量,由于目标存在多普勒模糊,脉间相位编码法的方法没有解多普勒模糊的能力,因此对于目标速度的提取错误,在速度精度结果中不再体现错误的结果。如图9(d)所示,由于本文所提算法使用了整个驻留时间的脉冲进行多普勒处理,多普勒分辨率明显高于多脉冲重频法的方法,而且在信噪比处理增益上也有提高。因此对于速度的测量精度,本文方法明显高于多脉冲重频法方法。对于不考虑多普勒敏感性的DFC波形方法,速度测量精度与本文所提方法相差不大,但是由于匹配滤波失配引起的信噪比损失影响了测量精度,使得其在不同信噪比下的起伏高于本文所提方法。 图9 目标检测及参数估计性能Fig.9 Target detection and parameter estimation performance 表4为不同方法对于距离和速度均方根误差(root mean sguare error, RMSE)的方差。从结果可以发现,本文方法对于目标距离和速度测量结果的方法均优于其他方法。 表4 目标测量结果RMSE方差 从以上仿真实验结果可以看出,本文所提方法可以准确解决PD雷达在MPRF下的距离-多普勒二维模糊问题,同时通过长时间相参积累以及精确匹配滤波,可以显著提高目标的检测性能以及参数测量精度。 机载脉冲多普勒雷达在MPRF工作模式下,目标回波可能存在距离-多普勒二维模糊,本文提出了循环发射正交DFC波形脉冲的方法,利用信号的正交性,在匹配滤波阶段进行距离模糊区域的区分,通过Keystone处理中搜索最佳相参积累增益下的补偿多普勒模糊数,实现多普勒解模糊,同时Keystone带来整个驻留时间的相参积累,增加了在低信噪比回波情况下的检测性能。为了解决相对速度较快带来的多普勒敏感性问题,采用了多普勒域匹配滤波的方法,通过滤波器的设计,可以准确有效解决多普勒敏感性问题。仿真实验验证了算法的有效性。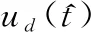
1.2 离散频率编码信号
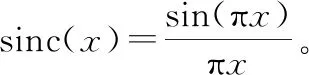
2 基于DFC的两维解模糊方法
2.1 回波处理流程框架
2.2 回波信号Keystone校正及多普勒模糊补偿

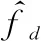
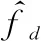
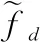
2.3 多普勒敏感性匹配滤波与解距离模糊
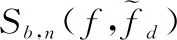
2.4 多普勒谱滤波融合
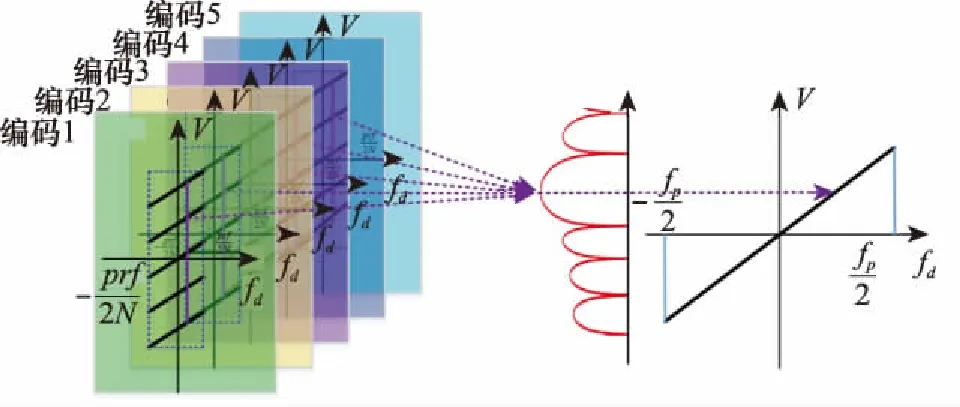
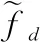
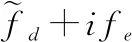
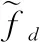

2.5 目标检测及多普勒模糊数确定
2.6 算法复杂度分析
3 仿真实验及性能分析


3.1 DFC解距离-多普勒两维模糊


3.2 信号能量及目标检测性能



4 结 论

