基于目标高斯分布的定位系统节点最优部署方法

周荣艳, 陈建峰, 李晓强, 谭伟杰

(1. 西北工业大学航海学院, 陕西 西安 710072; 2. 南阳理工学院, 河南 南阳 473004;3. 贵州大学公共大数据国家重点实验室, 贵州 贵阳 550025)

0 引 言

分布式定位系统的定位精度不仅依赖于传感器节点的定位算法、节点个数、采样频率等因素,节点的部署位置也是影响系统定位性能的重要因素之一[1-4]。节点部署算法能够在不改变定位算法和不增加节点个数的情况下,有效提高系统的定位精度,得到国内外学者的广泛研究,并逐步成为分布式定位系统研究中的一个重要分支[5-6]。

在目标探测与定位领域,克拉美罗界(Cramer-Rao bound, CRB)提供了任何无偏估计量方差所能达到的一个理论下界,并且CRB的表达式是关于目标与节点相对几何位置的非线性函数,因此常把CRB作为优化节点与目标相对位置的评价函数[7-10]。近年来,关于CRB的研究主要集中在两个方面:一是根据相关理论的推导得到针对某些特殊目标位置或接收特殊阵列时距离与角度估计的CRB[11-13];二是根据某一设计指标要求,按照相应的优化原则,将求解CRB的问题转化为最优化问题,采用智能优化算法进行迭代,寻优从而逼近CRB[14-15]。这些方法都是分析如何减小定位估计误差的CRB,虽然可以较好地提高目标在某一特定位置的定位精度,但并没有考虑目标服从高斯分布时定位误差的CRB。

文献[16]基于到达时间(time of arrival, TOA)定位算法,以最小化平均CRB为优化准则,得出基于节点观测性能的最优布局与声源出现概率分布直接相关的结论。文献[17]研究了目标服从高斯先验分布的条件下状态估计的协方差矩阵和信息矩阵,为传感器的选择和最优布局提供了衡量标准,并得出纯方位估计中视距的方向向量垂直于协方差矩阵最大特征向量的结论。此结论应用于文献[18]中,并对目标高斯先验分布下异构传感器网络中的节点进行优化配置,但需要将初始协方差矩阵进行若干次迭代更新,计算量大且较为复杂。

近年来有些学者通过分析坐标旋转在目标定位和探测方面的应用,为相关研究提供了新的思路。文献[19]证明了二维笛卡尔坐标系统中几何坐标平移与旋转对纯方位估计算法的伪线性估计(pseudolinear estimation, PLE)与最大似然估计(maximum likelihood estimation, MLE)没有影响,而总体最小二乘(total least squares, TLS)估计通过坐标旋转发生变化,并依此为基础提出了一种减小TLS估计偏差的算法,但并未考虑在三维空间中的相关问题。文献[20]通过对方位角和俯仰角的测量方程进行线性化,将未知节点估计转化为PLE模型求解,并证明了此三维伪线性估计算法通过笛卡尔坐标系旋转可以显著改变算法性能,从而有效地减小系统偏差。但此算法分别基于xy坐标轴与z坐标轴,并未对三维空间中的坐标系整体进行研究。

本文在其他学者研究的基础上采用到达角(angle of arrival, AOA)定位算法,首先基于目标高斯分布的FIM信息矩阵,研究满足CRB的条件;之后推导基于三维坐标旋转的最大后验概率估计(maximum a posteriori estimation, MAP)定位算法,将目标先验概率分布的非对角协方差矩阵转化为对角阵;得到满足CRB的最小迹时节点的最优部署位置。

1 问题描述

在三维空间中,假设一个目标声源的位置s=[x,y,z]T,N个具有三维测向能力的节点位置坐标pk=[px k,py k,pz k]T,k=1,2,…,N。如图1所示,任一节点对目标的观测都有方位角φk和俯仰角θk两个估计量,表示为

图1 三维AOA定位算法中方位角和俯仰角示意图Fig.1 Illustration of azimuth angle and elevation angle in three dimensional AOA positioning algorithm

(1)

(2)

在噪声环境中,角度测量值为真实的角度测量值和测量误差的叠加[21],即

(3)

(4)

Φ=M0+JTΣ-1J=

M0+Φ1+Φ2

(5)

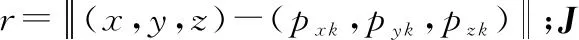
(6)

CRB为任何无偏估计量方差的确定下界,CRB为费希尔信息矩阵的逆矩阵。由文献[22]可知,三维空间中AOA定位算法估计误差的FIM可写为

(7)

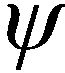
(8)

2 基于三维坐标旋转的MAP方法

2.1 MAP方法

p(s)=

(9)

由式(3)可得,角度测量值的似然函数为

(10)

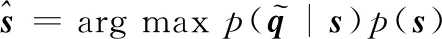
(11)

(12)

最大后验成本函数JMAP(s) 可表示为

(13)

则残差为

Γ(s)=[e(s);r(s)]

(14)

其中e(t)和r(t)为

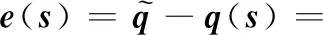
r(s)=s0-s

(15)

(16)

J1i=

(17)

式中:

(18)

设3×3矩阵J2i表示r(s)的雅克比矩阵,可得

(19)

将式(17)与式(19)结合,即可得式(13)雅克比矩阵

Ji=-[J1i;J2i]

(20)

采用高斯-牛顿算法对MAP进行计算,则可得迭代关系式[25]

(21)

2.2 基于三维坐标旋转的MAP方法

由式(8)可知,当目标位置误差的协方差矩阵P0=diag([a,b,c])时,则M0=diag([a-1,b-1,c-1]),由式(5)可知只需满足等号右边后两项Φ1与Φ2最小时，得到tr(CRB)的最小值。当P0为对称矩阵时,文献[17]通过将初始协方差矩阵P0进行若干次迭代更新，将其转化为对角阵，寻找纯方位定位算法中节点的最优部署方向,但计算量大且较为复杂。

由于目标的先验协方差矩阵P0在物理上相当于一个椭球,其内任一点都是目标可能出现的位置。因为三维坐标旋转并不影响椭球体的大小,且协方差矩阵P0对于任何相似变换UPUT具有不变性(其中U为酉矩阵)。可采用三维坐标旋转的方法将P0对角化,通过合适的绕x轴、y轴、z轴旋转角度α、β、γ组成的三维旋转矩阵R,将初始协方差矩阵P0对角化,即可得到tr(CRB)的最小值。

在本节中首先定义三维空间中的旋转矩阵,再对三维旋转后的MAP方法进行推导。定义三维空间中的坐标旋转矩阵如下所示。

(22)

其中α、β、γ分别为绕x轴、y轴、z轴逆时针的旋转角,如图2所示。

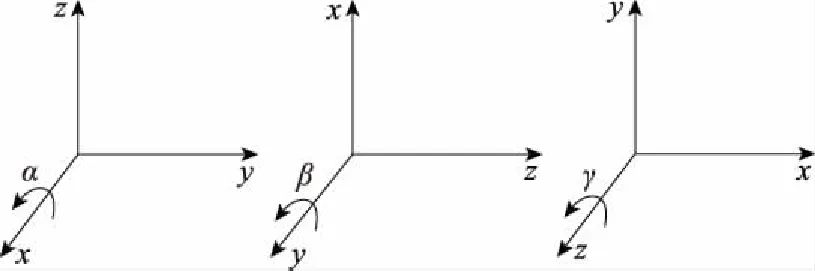
图2 绕x轴、y轴、z轴逆时针的旋转角 Fig 2 Rotation angle counterclockwise about the x -,y -,z - axis

R=RxRyRz

(23)

当三维空间中进行坐标旋转时,可得旋转后定位系统中各参量为

(24)

(25)

因此,旋转后的俯仰角和方位角表示为

(26)

为了计算旋转后的协方差矩阵可采用一阶泰勒级数近似来计算旋转后的角度噪声。将式(3)代入到式(26)中,可得

(27)

由误差传播定律可知,在三维旋转后,第k个节点的噪声协方差矩阵可以写为

(28)

旋转后包含噪声分量的角度估计为

(29)

旋转后的tr和qr计算得到无噪声的真实目标位置可写为

(30)

因此,旋转后的MAP 可表示为

(31)

采用式(24)中旋转后目标先验分布中的协方差矩阵,结合上式中的Kr,则MAP的协方差矩阵为

(32)

则式(31)可写为

(33)

残差为

Γ(sr)=[e(sr);r(sr)]

(34)

式中:

(35)

(36)

采用高斯牛顿法计算MAP,迭代关系式如下所示

(37)

2.3 最优节点部署方法

本节主要研究已知目标先验分布的情况下纯方位定位系统中节点的最优部署。首先,由第2.2节的结论可知,在目标声源服从高斯分布的假设下,三维坐标旋转能够解决目标先验协方差矩阵为非对角阵的问题,可通过三维坐标旋转的方法将目标先验分布中的非对角协方差矩阵转化为对角阵,所以在后续研究中,只考虑P0为对角阵时的CRB。由式(5)～式(8)可知CRB的迹为

tr(CRB)=tr(Φ-1)≥

(38)

当以下等式同时成立时,式(38)的等号成立。

(39)

由于通过三维旋转后P0为对角阵,则使CRB对角化的条件为[21]

(40)

满足式(40)的方位角的集合为

C={{θ1,θ2,…,θN}|θk∈{0,±π/2},k=1,2,…,N}

{{0,0,…,0},{±π/2,±π/2,…,±π/2}}

(41)

俯仰角的集合为

Z={{φ1,φ2,…,φN}|φk∈{0,±π/2},k=1,2,…,N}

{±π/2,±π/2,…,±π/2}

(42)

3 实验仿真

本节首先采用梯度下降算法,验证本文基于目标高斯分布的定位系统中节点最优部署方法。假设已知目标的先验概率分布,系统中有3个节点进行定位,并将节点位置随意放置,文献[21]中未经三维旋转的最优部署位置和本文方法得到的最优部署进行对比,证明本文方法的优越性。

3.1 最优节点部署方法实验验证

采用牛顿梯度下降算法对定位误差CRB的迹进行最小化迭代寻优[26],本实验仿真中对牛顿梯度下降算法执行10 000次。

实验 1目标声源和传感器之间的最小距离用r0表示,r01=r02=r03=100 m,s0=[0,0,0]T,协方差矩阵

σφ1=σφ2=0.5°,σφ3=1°。节点初始迭代坐标位置为p1=[100,-200,0],p2=[300,200,200],p3=[-200,100,-200]。图3(a)为节点从初始迭代位置移动到最优部署位置的迭代轨迹。目标在最终位置时的角度为θ1=-91.07°,θ2=89.07°,θ3=-178.07°,φ1=-0.06°,φ2=-0.013°,φ3=-88.76°。

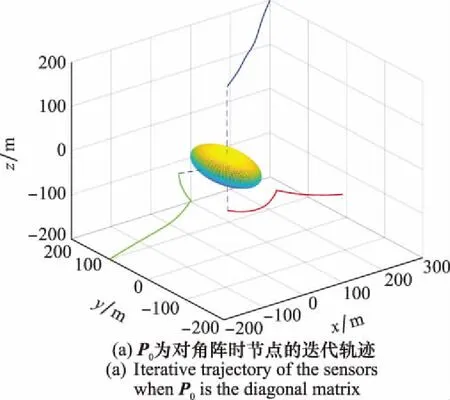
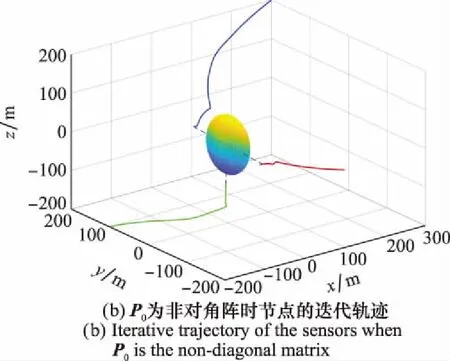
图3 节点迭代轨迹图Fig.3 Iterative trajectory of the sensors

实验 2在其他条件都不改变的条件下,设先验分布中的协方差矩阵为非对称矩阵

通过三维坐标旋转的方法将其转化为对称阵,旋转角度为α=14.5°,β=342.1°,γ=15.4°,可得到对角矩阵

图3(b)为节点从最初迭代位置到最优位置的迭代轨迹,最终角度为θ1=-92.12°,θ2=88.27°,θ3=-176.72°,φ1=-0.02°,φ2=-0.047°,φ3=-87.82°。

由此可知在协方差矩阵为对角阵和非对角阵的情况下,通过最小化CRB的迹得到节点最优部署,与理论推导结论一致。

3.2 节点部署对比实验

本节将3种不同部署方法所得CRB的迹进行对比,验证该算法的优越性如表1所示。

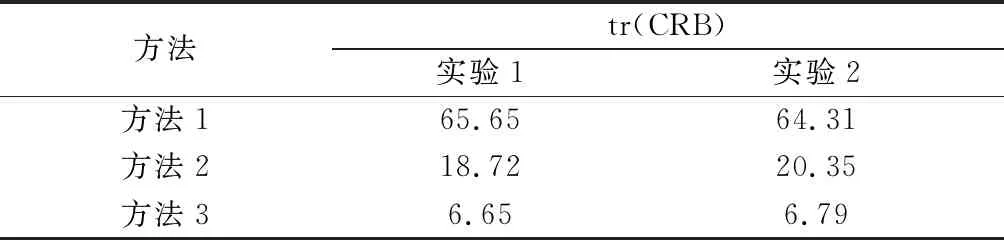
表1 3种节点部署tr(CRB)的对比

部署方法1:假设节点部署位置即为第3.1节中节点的初始迭代位置,其余条件相同。

部署方法2:文献[21]中3个节点的最优部署位置,即θ1=0°,θ2=90°,θ3=90°,φ1=90°,φ2=0°,φ3=0°。

部署方法3:第3.1节中节点部署位置。

由表1可知,随意位置部署时的tr(CRB)值较大,而文献[21]的结果由于受高斯分布中协方差矩阵的影响,也不再适用于此情况,通过三维旋转后得到的节点部署可获得tr(CRB)的最小值。

4 结 论

为了解决定位系统中目标位置服从高斯先验分布假设下的最优节点部署问题,本文探讨了基于三维坐标旋转的MAP方法,提出了一种基于目标高斯分布的求解克拉美罗下界的方法,并依此给出了最优的节点部署配置,最后通过梯度下降方法验证了理论推导的正确性。由于本文中最优部署方法是基于AOA定位算法,这也将在后续研究中为AOA节点定位算法的最优布局和节点选择等问题提供了理论指导和评价标准,以便在实际工程应用中获得最佳目标定位与探测性能。