脉冲噪声非线性变换设计的研究综述

罗忠涛, 郭人铭, 詹燕梅

(重庆邮电大学通信与信息工程学院, 重庆 400065)

0 引 言

高斯噪声普遍存在于大多数系统,但非高斯噪声在一些特定场景中有决定性影响。例如,长波通信中的大气噪声[1],电力线通信中的电晕效应等引起的脉冲[2-3]等,均含有大量的大幅值噪声样本。此类噪声在概率密度函数(probability density function, PDF)上表现为具有明显的厚拖尾,被称为脉冲噪声或脉冲性噪声[4]。当存在脉冲噪声时,基于匹配滤波的常规检测性能会显著下降,因此脉冲噪声下的稳健检测技术研究很有必要。

脉冲噪声抑制有多种途径,其中一类方法是自适应滤波,重点是设计滤波准则与算法,如恒虚警中值滤波[5]、最小分散系数准则[6]、最大相关熵准则[7]、对数最小平均次幂准则[8]等。不过,此类方法在应用上比零记忆非线性(zero-memory nonlinearity, ZMNL)变换更复杂。

本文关注针对平稳脉冲白噪声的非线性变换设计。此设计的应用结构很简单，只需在常规匹配滤波之前增加一个非线性处理器。其技术原理来自统计信号处理理论[9]。最大似然检测是最优检测器[9-10],在低信噪比(signal to noise ratio，SNR)下可近似为局部最优检测(locally optimal detection，LOD)，然后使用LOD结构而设计非线性变换函数。

为此，待解决问题可以描述为：在脉冲噪声下，如何设计非线性变换函数，以提高检测性能。近半个世纪以来，学者们在脉冲噪声的非线性变换函数设计上一直开展着研究。

本文首先介绍针对脉冲噪声的非线性设计问题，然后综述工作将从噪声模型、函数模式与设计方法3个方面梳理现有研究，再总结研究路线和成果上的共性规律。

1 非线性变换设计问题

根据统计信号处理理论，考虑基于M个样本的信号检测问题，设接收信号模型为

r(m)=Aisi(m)+w(m)

(1)

式中:r(m)表示接收数据;si(m)表示第i假设下的待检测确定性波形;Ai表示该波形的幅度;w(m)表示加性脉冲白噪声,即w(m)独立同分布,m=1,2,…,M。

设噪声PDF为f(x),可得最大似然检测为

(2)

即,将取得最大似然函数的假设判决为真[9]。最大似然检测具有理论上的最优检测性能,但检测器要求波形幅度Ai已知,且运算量较大,故实际运用很少[10]。

考虑低SNR下的近似最优检测问题时,设信号幅度Ai为非负,最大似然检测可近似为局部最优检测,为

(3)

式中:glo(x)=-f′(x)/f(x)表示ZMNL变换[9]。

LOD结构可理解为:先对数据r(m)进行非线性变换,再连接至传统相关检测。可见此结构与传统匹配滤波器很接近。不过,f(x)常无闭合表达式,导致glo(x)需要数值计算,比较麻烦,故LOD也不易应用。

对此,延用LOD结构而修改其ZMNL函数。具体而言,使用另一非线性变换函数,再后接匹配滤波处理,最终检测器可记为

(4)

式中:g(x)为非线性变换函数。毫无疑问，g(x)对于检测性能非常关键。

一般g(x)继承了glo(x)的3个特点：为ZMNL奇函数；具有线性或近似线性区域，以及非线性区域；非线性区域对大幅值样本形成抑制效果。

最终，非线性变换设计变成了如下问题：针对脉冲噪声w(m)，设计非线性函数g(x)，使判决器式(4)的检测性能达到最优。

显然，g(x)与噪声分布有密切关系；g(x)函数构造的模式需要考虑设计；g(x)函数的参数优化又牵涉到设计方法和准则问题。这是非线性变换设计问题的3个要素，下面逐一进行介绍。

2 脉冲噪声分布模型

脉冲噪声的研究和处理离不开噪声建模。目前已采用的脉冲噪声分布模型可大致分为3类，包括对称α稳定(symmetricαstable, SαS)模型、Class A模型和混合模型。不同模型各具特点，并不统一也不等价。不过，其共同点是零均值和对称分布。

2.1 SαS分布

α稳定分布是唯一一类满足广义中心极限定理的统计分布[11],SαS分布是均值为0、对称的α稳定分布,在脉冲噪声中应用非常广,研究也很深入[11-12]。除特例柯西分布(α=1)和高斯分布(α=2)以外,SαS分布PDF无闭合表达式,只可通过其特征函数来计算:

fSαS(x)=IFT[exp(-γ|ω|α)]

(5)

式中:0<α≤2表示特征指数;γ是分散系数;ω是角频率;IFT(·)表示逆傅里叶变换。参数α越小,噪声脉冲性越强,一般α在[1,2]区间内。当α<2时,SαS分布的方差或2阶矩不存在。

当SαS分布无闭合PDF而只能数值仿真时,需适当设置幅度值x的大小范围。并且,理论上fSαS(x)为实偶函数,但注意逆傅里叶变换的程序运算可能存在虚数部分。

2.2 Class A分布

20世纪70年代,Middleton等人在考虑噪声源属性和噪声时间、空间、传播等分布的基础上,推导出噪声特征函数进而得到了3类噪声模型[13-14]。其中,Class A模型常被用于脉冲噪声研究,其PDF为

(6)

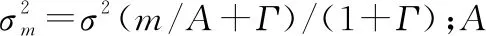
Class A分布的PDF可视为无穷级数求和,无闭合表达式。数值仿真时需注意控制m的取值范围。

2.3 混合模型

混合模型的建模思路是:以小方差高斯噪声作为背景噪声,以大方差噪声作为脉冲分量,二者相加构造出混合噪声。目前高斯混合模型[15]最为常用,其次是柯西-高斯混合模型[16-17]和高斯-拉普拉斯混合模型[18-19]。此类模型的PDF可统一表示为

(7)

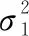
混合模型也可采用多分量,如K分量高斯混合模型[20-21],以K=0的高斯分量表示背景高斯噪声,其余K>0的高斯分量具有较大方差,表示脉冲噪声。

实际上,混合模型也可看作一个随机过程。该过程每个样本以一定几率取背景噪声或脉冲噪声。例如,二分量混合模型等价于伯努利-高斯模型[22-23],每个样本的高斯成分或脉冲成分的发生概率服从伯努利分布。此外,随机过程也可灵活定义,例如文献[24]将噪声建模为Nakagami-m分布,脉冲成分为Class A分布,其发生概率服从泊松分布。

2.4 小结

本节简述了脉冲噪声研究中常用的噪声模型。总体而言,SαS模型的PDF没有解析式,没有单独分量独立表示背景噪声,但满足广义中心极限定理,应用最为广泛。Class A模型和高斯混合模型应用也较多,其中高斯混合分布可视为简化的Class A分布。混合模型的优势在于具有闭合PDF,便于分析和计算。

实际工程问题和具体场景中脉冲噪声的模型选择,需针对具体情况展开具体分析。例如,一个基本办法是:录取场景噪声数据并预处理至非线性变换前,采用分布假设检验、幅度分布曲线对比、Q-Q图分位数观察等统计理论方法,来确定描述该噪声分布的最佳模型。不同场景的脉冲噪声可能服从不同的分布。例如,蒋宇中判断Class A模型可以很好地描述宽带超低频信道大气噪声幅度统计特性[25];而罗忠涛录取大气噪声数据并白化滤波后的噪声分布检验和PDF对比表明,其幅度近似服从SαS分布[26]。

3 非线性函数模式

脉冲噪声模型具有不同的PDF,导致其LOD非线性函数glo(x)也不相同。显然,这要求设计出不同的非线性变换函数。本节梳理常用的人造非线性变换函数模式,其共同点是:具有线性或近似线性区域,门限可供调整设计;在门限内数据保持不变,超过门限则进行非线性变换。非线性函数的模式大致可分为5种。

3.1 削波与置零拖尾

削波器和置零器出现得非常早,运算也极为简单[11，27],可分别记为

(9)

式中:T为线性区域的门限;sgn(x)为符号函数。削波和置零处理可描述为:当数据幅度不超过门限时,直接输出;当数据幅度超过门限,则认为受到脉冲噪声影响,进行置零或按固定值输出。此外,符号检测器也曾出现过[12，28],但近来已不见讨论应用。

由于削波或置零处理对大幅度脉冲有显著抑制作用,限幅处理在抑制脉冲噪声中很有效,其中限幅门限T对抑制效果有决定性影响,最优抑制效果也与噪声分布有关。现有研究表明,在SαS噪声中削波器比置零器性能更好;在Class A噪声中,置零器比削波器性能更好[29]。这说明置零器和削波器都不适合用于多种噪声分布。

3.2 多区域组合拖尾

相比削波器和置零器的非线性区域只有一个函数,后期研究设计出更为复杂的拖尾,增加设计自由度以提高检测性能。比如,文献[30]将削波和置零进行简单组合,采用两个门限分出多个非线性区域,分别采用削波和置零处理。非线性函数可写为

(10)

式中:T1和T2为不同的门限。进一步地,文献[31]提出将非线性区域[T1,T2]进行一定减幅,从而形成深度削波。文献[32]的性能分析表明,深度削波技术优于单纯削波、置零或二者的组合。

在拖尾中设计多重门限和非线性区域也可行。针对K分量高斯混合模型,文献[21]提出了多门限的拖尾设计。门限个数可人为调整,各段非线性区域的非线性变换可能是不同水平的削波处理,或者不同斜率的线性函数。

从组合拖尾的发展历程来看,在传统削波和置零处理的基础上,增加非线性区域数和改变削波电平,能够增加设计自由度并在一定程度上提高噪声抑制性能。不过,组合拖尾设计越精细,非线性变换的分段函数越多,引入的门限和电平参数也越多,函数表达式、性能分析和参数优化就越复杂。

3.3 单参数特定拖尾

削波或置零处理输出固定幅度,实际上脉冲噪声模型的LOD非线性函数为曲线,因此学者们也提出了基于特定函数的曲线拖尾函数。

在2002年Swami等人提出GZMNL (Gaussian-tailed ZMNL)函数[33],为

(11)

式中:σ为拖尾参数。针对SαS噪声,GZMNL的σ可由SαS分散系数标准差除以0.7得到;针对不同α,T的取值应当在σ～3σ内。但是,T值区间的性能上下限差距太大,传统GZMNL极不稳健。

文献[34]针对SαS分布提出的AZMNL(Algebraic-tailed ZMNL)取1/x为拖尾,既有闭合表达式,又实现了比削波器明显更优的检测性能[35]。

3.4 单参数非分段函数

某些ZMNL函数采用单一表达式而非分段函数,其线性区域不是严格线性而是近似线性。例如,针对柯西分布噪声,其LOD非线性变换函数为

(12)

既在较小|x|区域内具有近似线性,又在|x|区域外具有明显非线性。

柯西LOD非线性采用单一表达式且同时兼具线性与非线性的要求,得到了研究者的关注。文献[36]提出一种柯西LOD非线性变换的推广形式:

(13)

式中:λ和β为待定参数,增加了函数设计自由度。Dai等人对柯西LOD推广式进行了简化,并通过参数优化使其在SαS噪声中取得非常接近LOD的性能。同时,提出另一种非线性函数[37],即

ggg(x,T)=xe-Tx2

(14)

式中:参数T同时控制了近似线性区域的范围和拖尾衰减的速度。此外,王平波等人还提出采用Sigmoid函数来构造非线性函数[38],即

(15)

式中:k>0为待定参数,控制对噪声的抑制程度。

3.5 双参数可变拖尾

以上非线性函数共有缺点是拖尾函数不够灵活,线性区域的门限和拖尾函数不能独立调整。实际上,观察LOD可见,最佳非线性即glo(x)=-f′(x)/f(x)直接取决于噪声PDF。如果ZMNL函数g(x)的拖尾相对固定,仅优化其门限或单参数,难以满足对不同噪声分布的LOD非线性变换的近似。

对此,罗忠涛等人提出一个新的思路:构造双参数的非线性变换函数,一个参数控制线性区域门限,另一个参数控制拖尾衰减速度[39]。比如,以指数函数为拖尾的非线性函数设计为

(16)

式中:底数a∈(0,1]。通过调整a值,非线性函数可对大幅值样本实现不同程度的抑制[39]。相似地,也可以幂函数xb为原型设计拖尾,通过调整指数参数b来实现可变拖尾的非线性设计[40]。此外,传统GZMNL函数的高斯拖尾因子σ也可控制拖尾衰减速度[41],但是以往的研究没有重视这一点。

3.6 小结

本节简述和归纳了常见的非线性变换的函数模式。图1为典型非线性函数的示意图，其中GGM表示高斯化-广义匹配(Gaussianization and generalized matching, GGM)滤波方法。

图1 常用的非线性函数模式Fig.1 Widely-used nonlinearity functions

人为构造的非线性变换大多可分割为线性区域和非线性区域。对于非线性区域,削波或置零的限幅处理最为传统,信号处理也最简单;结合多个非线性区域和抑制水平的组合拖尾设计,能在一定程度上提升抑制能力,但函数过于复杂且参数较多;单一表达式的非分段函数,以单一参数同时控制其近似线性区域和拖尾衰减速度;最后,双参数拖尾函数设计,可独立调节线性区域门限和非线性区域抑制程度,故能适应不同分布。并且,相比于多区域混合方法,可变拖尾的表达式更简洁,便于计算和分析。

4 设计方法与准则

非线性变换在确定函数模式之后,还需对函数中的待定参数进行设计和优化。噪声冲击性强弱等特性会反映在模型参数上,而非线性变换函数必须自适应设计才能优化对该噪声的抑制效果。非线性函数设计准则和设计方法有多种,归纳总结为大致4种:基于分析近似方法、基于正态变换方法、最大输出SNR法以及最大效能准则。

4.1 分析近似方法

分析近似方法的分析对象可以是噪声数据、PDF规律和LOD非线性函数,分析结果是为非线性函数的待定参数赋值。

通过反复试验,观察不同参数值对检测性能的影响,可为非线性函数参数赋值提供宝贵经验。例如,Swami等人在提出GZMNL时,门限和拖尾方差参数是凭经验赋值为某区间内[33]。张杨勇等人对大气噪声采用削波处理的门限是按照幅度概率来选取,而此概率值取决于人工经验[27]。这种做法虽然看似粗糙,但在噪声分布认识不足的情况下却是稳健且有效的选择。并且,该方法的设计与处理运算很简单,故在长波通信中经常使用。

在噪声分布信息可知时,非线性变换的精细设计变为可能。一个思路是,既然LOD是最佳非线性变换函数,如能优化非线性函数参数以使其与LOD达到某种意义上的近似,那么设计的非线性函数也应当能够趋近LOD的最优性。例如,文献[36]提出了柯西非线性推广式后,再在最小2范数距离或最小均方差准则下优化参数(λ,β)。

直接分析PDF,根据LOD计算特性展开近似,也可为非线性函数设计提供指导和参考。文献[34]分析了SαS分布PDF的渐近幂级数表达式,从极限的角度将非线性区域的拖尾函数近似取为1/x,再在均方差最小准则下完成线性区域门限的设计[36]。文献[42]简化了Class A分布为高斯混合分布,将高斯成分和非高斯成分PDF相等点作为削波门限。文献[43]基于对Class A噪声PDF公式和LOD曲线的分析,分别设计了削波和置零的门限值。

4.2 正态变换方法

将接收数据进行正态变换,也是一个抑制脉冲噪声的有效办法。王平波等人分析的G滤波非线性变换函数[44]为

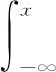
(17)

式中:F(x)表示脉冲噪声分布的累积分布函数;Φ(x)表示正态分布的累积分布函数。采用高斯混合分布,王平波对比分析了高斯化滤波与LOD非线性变换的曲线差异。后来,Li等人先后运用双参数高斯-柯西混合模型近似SαS分布,设计了基于正态变换的次优接收机[45-46]。

正态变换只能取得次优检测性能。罗忠涛等人将正态变换与广义匹配滤波相结合[47],提出一种新的非线性变换函数,即

(18)

分析表明,GGM方法可取得比正态变换更优的检测性能,且能适用于噪声分布未知的情况。

换个角度看,正态化或GGM方法的非线性函数没有刻意设计线性或非线性区域,而是与LOD一样完全依赖于噪声PDF。不过,尽管正态化或GGM处理对脉冲噪声具有抑制效果,但其抑制原理并没有相关理论支撑,并且检测性能与LOD也有明显差距。罗忠涛等人对仿真与实测数据的检测仿真表明,非线性变换输出数据正态性与检测性能之间不存在正相关的必然联系[26]。

4.3 最大SNR法

相比PDF分析或数据正态性,检测性能更有理由成为非线性设计优劣的判断标准。脉冲噪声影响下信号检测的常见指标有通信系统的误码率指标和有无判决的虚警-检测概率指标。如能在给定传播信道下针对某个检测器,推导出检测统计量或其分布与非线性变换g(x)的关系,就可以想办法来寻找最优化指标的参数值。文献[48]分析削波器对检测判决门限的直接影响,以最大化条件正确概率和条件虚警概率之差为目标。王平波等人考虑信号有无的检测问题,推导了检测统计量的分布,给出了恒虚警下检测概率与Sigmoid函数参数[38]和限幅器参数[49]的关系。

检测统计量和检测性能的推导可能比较复杂,非线性变换输出SNR无疑是一个很有意义的指标。Zhidkov针对伯努利-高斯随机过程的脉冲噪声,分析了置零器门限对输出SNR的影响[22],又分析了削波、置零及混合方法的输出SNR[30]。文献[32]增加了对深度削波的分析,并采用拟牛顿法寻找输出SNR的最大值。大部分最大化SNR的分析方法采用了高斯混合分布作为噪声模型,因为该分布公式比较简单,有利于SNR分析。

针对脉冲噪声下的电力线通信,Rabie等人近年来做了大量工作[15,50-52]。针对Class A模型及高斯混合模型,以最大输出SNR为准则,侧重考虑正交频分多路复用信号峰值功率对脉冲噪声参数估计的影响,提出置零器门限选择的动态方案。文献[52]提出了一种新的正交频分多路复用方案,可降低脉冲噪声对SNR的影响。

4.4 最大效能准则

在多样本检测中样本数较大时,SNR可由效能函数很好地衡量。效能函数的来源是:针对信号模型式(1)的确定性信号检测问题,在较低SNR下,当非线性变换g(x)输出的方差有界且样本数较大(如M>100)时,式(4)中检测统计量近似服从高斯分布。将输出SNR计算式中与噪声分布f(x)和非线性函数g(x)的有关项定义为效能函数：

(19)

式中:θ表示非线性函数的参数向量。

效能函数的详细推导可参考文献[9],文献[35]也有类似的推导。文献[38]推导的偏移系数可视为效能函数在具体情况下的一个变形。效能函数与SNR直接相关,直接决定了系统的通信性能和虚警-检测性能。

考虑噪声分布f(x)一定时,效能函数仅取决于g(x),故能很好地表征g(x)的优劣。对于式(19),可从理论上证明最大效能值由glo(x)取得,与LOD推导结果相符。不过,非线性设计研究在很长时间内都没有重视效能函数,只是将其用于性能验证。Vastola计算了Class A噪声中削波、置零和符号处理在不同门限下的效能值,并与LOD相比较[28]。Hyungkook基于PDF分析设定限幅器门限,采用效能作性能验证[43,53]。

效能函数不仅可作验证指标,而且可以直接作为设计指标。如此一来,非线性函数设计问题变成了参数寻优问题,即

(20)

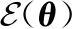
最大效能准则的数值求解方法是其关键。罗忠涛等人分别仿真了SαS和Class A噪声中削波和置零两种非线性函数的效能函数特性[29],因其是削波/置零门限的光滑凸函数,故用线搜索方法自动求解,其结果与文献[54]吻合。

对于双参数非线性函数,效能函数最大化问题转化为二维数值寻优问题[39-41]。通过理论证明或仿真验证可得,基于常用噪声模型如SαS、Class A和高斯混合噪声的效能函数曲面,是关于参数的连续、光滑和一定区域内的凸函数。因此,采用Powell方法或单纯形法等数值寻优工具来解决此类问题[55-57]。

4.5 小结

非线性变换设计的最终目标是提高信号检测的性能。尽管有时需要考虑信号本身的影响,但大多数情况下非线性变换的性能主要取决于噪声。毕竟,信号检测之所以困难,就是因为信号幅度相对于噪声来说过低,而此时基于多样本的信号检测成为必要。效能函数直接决定了输出SNR,最大化效能就意味着最大SNR。此外,对于少量样本检测问题,基于中心极限定理的效能或SNR方法不再成立,但其他方法继续有效。

在4种设计方法中,分析近似方法常用于对噪声PDF或LOD非线性函数的分析和近似,后来又应用于非线性函数最优参数的近似计算。这是因为,最大SNR或最大效能准则下的非线性函数g(x)的参数值往往是数值计算,不利于实时获取,因此可采用某函数近似描述g(x)参数与噪声参数的关系,给出g(x)参数的解析计算式[41,49,54]。

5 研究路线与规律

上文对脉冲噪声非线性变换的设计研究进行了3个方面的梳理,归纳了大部分研究工作主要涉及到的噪声模型、非线性函数模式和设计方法与准则。本节总结常见研究技术路线的共性规律,举例展示部分最新研究进展,以及本领域研究的一些有用成果。

5.1 常见研究路线

非线性变换设计中常见的研究路线可归纳为:针对某噪声模型(SαS分布、Class A分布、混合分布及其他分布的一种或多种),采用某非线性函数模式(置零、削波、柯西推广、指数拖尾等其中一种),根据某种设计方法或准则(分析近似方法、最大SNR及最大效能等其中一种),来优化设计非线性函数的待定参数,达到抑制脉冲噪声和提升检测性能的效果。

该研究路线既符合实际信号处理问题的研究需要,也在很多团队研究工作中得以采用和遵循。下面列举3个技术路线研究实例,同时也展示本领域的最新进展。

(1) 基于Class A噪声PDF分析的非线性设计

Hyungkook团队从2014年至2017年在Class A脉冲噪声抑制方面做了不少工作。例如,文献[43]以Class A分布为脉冲噪声建模,然后采用置零器gbl(x,T)和削波器gcl(x,T)抑制噪声,最后采用分析近似法去设计待定门限参数T,分析Class A分布PDF与LOD曲线特点,对比置零和削波函数曲线。将置零器门限设置为

(21)

而削波器门限被设置为

(22)

仿真表明,所设计的置零器非常接近LOD效能,但削波器差距较大。

针对具体噪声PDF或LOD分析获得的非线性函数设计方法的针对性很强,但适用噪声范围受限。不过,此类研究提供了解析函数,便于使用。

(2) 基于偏振系数的单参数非线性函数优化

王平波团队长期从事脉冲噪声的抑制研究工作,近年来研究恒虚警检测问题,推导了检测统计量的渐近分布,得到关于检测概率的关键参量即偏移系数[37-38,49],该系数与噪声分布和非线性函数的相关量为

(23)

实际上该参量与效能函数是等价的,因为脉冲噪声f(x)和非线性函数g(x)性质满足等式:

(24)

王平波等人以偏移系数为优化目标,分析了单参数非线性函数的最优参数值,再通过近似拟合法,提出了非线性函数参数的快速赋值方法。

对于高斯混合噪声,将Sigmoid函数式的参数赋值为

kop,dw≈2/σ1

(25)

而削波器式(9)的门限应当赋值为

Top,dw≈σ1

(26)

对于SαS噪声,柯西推广的非线性函数式的参数近似赋值为

β2op,dw=γα/2(17 730e-11.75α+18.15e-3.03α)

(27)

而式(13)中参数λ本身不影响检测性能。仿真表明,柯西推广非线性在SαS噪声中的最优效能是LOD效能的99%以上,但在Class A噪声中会下降到93%以下。

(3) 基于效能最优的双参数非线性函数设计

罗忠涛等人的非线性设计研究注重“为各种分布的脉冲噪声”提出“一个统一的最优抑制解决方法”[39],达到了优化目标、非线性函数和优化方法3个方面的统一。

首先,尽管不同噪声的LOD差异很大,但低SNR下的检测性能都可以用效能函数式来衡量,因此效能函数可作为统一的优化目标。

其次,传统非线性函数模式只适用于一种噪声分布。例如,削波器较适合SαS噪声,而置零器更适合Class A噪声[29]。这说明不同噪声分布要求有不同的拖尾函数。为此,罗忠涛等人提出了具有可变拖尾的双参数非线性函数模式[39]。

最后,最大效能准则下的双参数非线性设计问题转化成二维数值寻优问题。例如,指数拖尾非线性函数设计问题描述为

(28)

该问题可采用一般数值寻优工具求解,适用于各种噪声分布,设计结果在SαS、Class A和高斯混合分布中均能取得LOD效能的99%以上。

此外,为实现非线性函数参数计算的实时性,罗忠涛等人提出了两种快速设计方法[41]。一是考虑ZMNL函数g(x)的参数为噪声模型参数的函数,基于多项式拟合思路并估计各阶系数,然后可快速计算出g(x)参数;二是绘制噪声参数与g(x)最优参数的表格,使用时查找实时噪声参数位置,再插值计算对应的g(x)参数值。

5.2 研究成果和规律

纵观现有的大部分非线性变换设计,关于研究发展和工作成果及其规律小结如下。

(1) 噪声分布无大改变,对象从单一到多种。目前常用的脉冲噪声模型在20年前早已有之。不过,以往研究常针对单一噪声模型提出非线性设计方法,而罗忠涛等人研究针对多种噪声模型的统一解决方法。实际运用时,如能确定噪声模型及其参数,则既可用符合该模型的设计方法,又可采用统一设计方法。如果噪声PDF不符合已知分布,最大效能准则依然适用。

(2) 非线性函数多样化,模式种类在扩展。传统非线性函数是置零器和削波器,后来发展出组合拖尾、新的非分段函数和可变拖尾模式,得到了多样化的非线性函数。相比传统非线性函数,新提出的非线性函数的参数物理意义不明显。但是,归功于设计准则和数理方法的发展,新非线性参数可通过数值优化和近似拟合得以有效设计,其检测性能超过了传统函数。

(3) 最优化理论和数值优化方法提供了新思路。效能函数在1984年已用于性能验证,但长期不得重用,其原因可能是所含计算过于复杂而难以直接用于ZMNL设计。借助于近20年长足发展的最优化理论和数值优化方法,效能最优化问题得以解决。在理论推导效能函数部分特性和仿真验证其局部凸性后,采用一般数值优化工具即可解决非线性函数的参数优化问题。图2描绘了SαS分布γ=1下多种非线性变换的最优效能,其中置零、削波、柯西推广、以及指数拖尾(双参数可变拖尾)均采用单纯形法寻优。由图2可见,LOD具有理论上的最高效能;双参数非线性的最优效能达到了LOD的99%以上,在检测性能上非常理想;柯西推广非线性与指数拖尾几乎相同,性能损失不到1 dB;削波器和置零器明显更差,只能算次优。

图2 SαS噪声中非线性函数的最优效能Fig.2 Optimal efficacy of nonlinearity function in the SαS noise

最后再仿真Class A噪声下多种非线性变换的MSK通信误码率。参数设置为A=0.1,Γ=0.01,σ=1,M=144。逐位检测误码率的蒙特卡罗实验结果如图3所示。

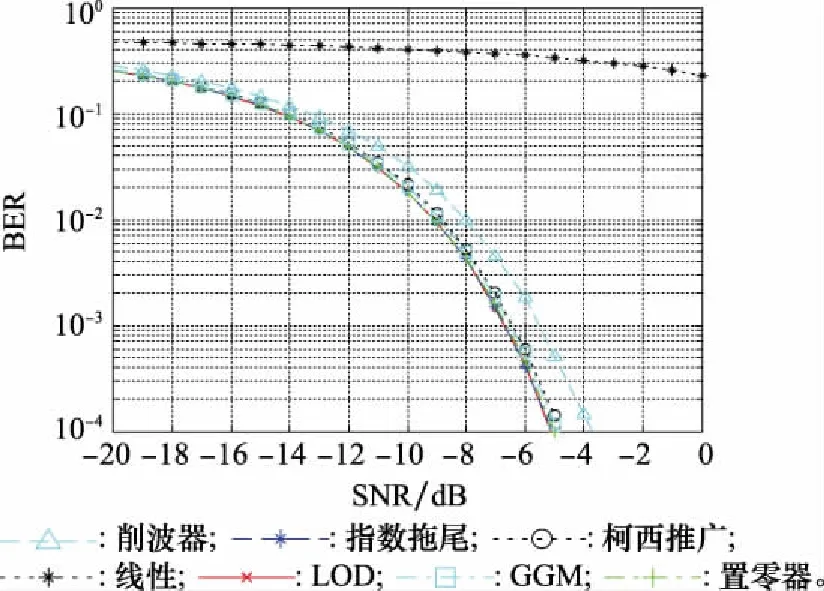
图3 MSK通信误码率仿真Fig.3 Simulation of MSK communication bit error ratios

总体看来,LOD、置零器和指数拖尾的误码率性能为最优;GGM和柯西推广有微弱下降;削波器下降明显;不采用非线性处理的线性相关检测性能极差。

6 未解问题与展望

对于脉冲噪声非线性变换的研究已经持续近半个世纪。在函数设计上,从简单的取符号、置零和削波处理,发展为结合置零/削波/深度削波的组合拖尾,再到能够很好拟合LOD非线性函数的双参数非线性函数。针对低SNR下多样本检测情形,以效能最大化为优化目标,设计的双参数非线性变换已经能够达到与LOD几乎相同的性能。在检测性能已很满意的情况下,非线性变换函数设计的研究可以着眼于以下两个问题。

6.1 噪声分布未知

噪声分布未知的情况可分为两种。

一是噪声模型已知,但分布参数未知,可采用参数估计算法。例如,SαS模型可采用基于样本分位数的参数估计方法[11],Class A模型可采用基于样本模值分布的参数估计方法[58]。基于模型参数估计值,得到PDF估计,再使用噪声分布已知下的非线性函数设计方法。

二是噪声模型未知,可采用核密度估计(kernel density estimation, KDE)方法[59]。设观测样本Xn,n=1,2,…,N, 由KDE得其PDF估计为

(29)

式中:K(x)表示核函数,一般具有零值对称性;h控制核函数的宽度。针对脉冲噪声,一种有效且稳健的赋值方法为

h=0.79N-1/5RIQ

(30)

式中:RIQ为四分间距,表示对噪声方差的一种衡量[60]。

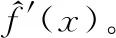
6.2 改进效能寻优

对于最大效能准则,最优可变拖尾设计在已知PDF噪声下可取得LOD效能的99%。不过,目前研究和算法设计还存在两个问题。

(1) 效能关于待设计参数的函数特性没有完整的理论证明。对于某些非线性函数,可以证明效能函数是连续和分段可微的[40],但是其单调性或凸性却难以进行理论分析。

(2) 效能函数及其偏导数均无解析式,只能采用数值计算。效能公式中的积分项只能用向量求和近似,这会涉及到f(x)的x取值范围和间隔设置。并且,寻优算法需要多次迭代计算效能,最终导致设计算法的运算量较大。

优化算法的迭代次数与参数初始值非常相关,通过合理设置可以加快寻优速度。目前看来,个人电脑能在数秒内完成参数寻优,但一些运算能力较差的设备就难以完成实时设计。因此,有必要开展进一步研究,改进效能函数运算或优化算法以提高寻优效率。

如能预测某场景可能出现的噪声分布,则可采用离线方法实现快速设计。针对可能出现的噪声进行离线设计,建立噪声分布与最优参数的对应数据库,或者建立非线性变换参数关于噪声分布参数的近似函数关系[43],即可取得最优可变拖尾的解析式,满足非线性函数设计在速度和性能上的要求。

6.3 展望未来研究

针对低SNR下多样本检测问题,目前的非线性变换设计已能取得基本最优性能。对于未来可能的研究,有以下3个方面。

(1) 分布未知情形下非线性变换的稳健设计。可设计PDF一阶导数的估计方法以提高其精度和稳健性,或者转换效能计算公式以规避一阶导数运算。比如,积分运算对于估计误差的容忍度比求导运算更好,这也是高斯化和GGM方法的优点。

(2) 简化效能寻优算法,提高寻优算法效率。深入分析效能函数计算方法,改进效能计算和数值寻优算法,减少效能公式所含的数值运算,尽量替代为闭合表达式,提高优化算法的运算效率。

(3) 将现有方法运用于有色或非平稳脉冲噪声研究。虽然本文讨论的脉冲噪声是独立同分布的平稳随机过程,考虑脉冲噪声可能时变或与同频干扰并存环境[61],本文综述的设计方法也有一定的参考价值。

7 结束语

本文对脉冲噪声下的非线性变换设计的研究进展进行了比较系统的综述。从脉冲噪声的分布模型、非线性函数的模式、设计方法或准则3个方面,对国内外研究进行了梳理。总结了大部分研究工作的技术路线,即“针对某噪声模型,采用某非线性函数,基于某设计方法,优化该函数参数,以提升检测性能”,并介绍了3个代表性研究工作作为实例。

最后,考虑检测困难问题大多出现在低SNR下,针对基于多样本的信号检测问题,结合最大效能准则的可变衰减拖尾设计,所得非线性变换能够实现与LOD基本相同的检测性能。该方法针对各种噪声模型均有效,且其闭合表达式有利于信号处理。在检测性能基本达到上限的情况下,未来研究可着眼于改进设计方法以适应噪声分布未知和较小运算量的要求,也为非平稳/有色脉冲噪声处理带来新信息。