基于非线性模型预测控制的火星大气进入智能制导方法
胥 彪, 李 翔, 李 爽,*, 张金鹏
(1. 南京航空航天大学航天学院, 江苏 南京 210016; 2. 中国空空导弹研究院, 河南 洛阳 471009;3. 航空制导武器航空科技重点实验室, 河南 洛阳 471009)
0 引 言
火星作为地球的邻近行星,在很多方面都与地球相似,已经成为人类进行深空探测的重要目标天体。火星大气层非常稀薄,具有很大的不确定性,时常出现狂风、沙尘等天气。在探测器进入、下降与着陆过程中,大气进入段历时最久,工作条件最恶劣,飞行状态变化快,对减速性能的要求极高。
目前大气进入制导方法一般分为参考轨迹制导和预测校正制导[1]。参考轨迹制导方法首先按照要求设计好离线参考剖面(如阻力加速度剖面),然后根据实时跟踪误差设计制导律来在线跟踪这条轨迹。该方法易于实现,但制导性能受进入过程中各种不确定性的影响较大。预测校正制导方法是在飞行过程中不断预测终端状态,然后根据与期望终端状态的偏差校正控制量,具有较高的落点精度,并且对进入的初始条件不敏感。但其计算复杂度较高,需要较强的计算机性能以提高计算速度,在线制导的实时性难以保证。文献[2]比较了这两种方法,并从仿真研究中得出参考轨迹制导方案更适合火星大气进入段制导任务的结论。
近年来参考轨迹制导方法取得了许多研究进展。PID控制律已成功运用到了阿波罗飞船和航天飞机的再入制导[3],但其基于一些线性假设条件,且增益系数的整定比较麻烦。文献[4]使用反馈线性化的思想,利用状态反馈项来抵消阻力动力学的非线性。然而,在存在较大模型误差以及出现控制饱和现象时,其轨迹跟踪的性能很不理想。在此基础上,有些学者提出利用滑模状态观测器估计模型误差来提高控制精度[5],但是由于滑模本身的特点,得到的控制量存在抖动,对滚转角执行机构带来较大挑战。模型参考自适应方法也被用于火星大气进入制导[6],跟踪性能有所提高,但控制输入仍存在抖动现象。文献[7]采用了自抗扰控制方法进行跟踪,输入相对平滑,能够获得较高的跟踪精度。但是以上跟踪方法都未考虑实际存在的控制量约束,大都存在控制饱和的问题,不可避免地会导致在线跟踪的效果变差。
模型预测控制(model predictive control, MPC)方法是目前应用于工业过程中最常见的先进控制技术之一,近年来也被应用到了大气进入制导问题,能够很好地解决跟踪参考轨迹时存在的控制饱和问题。针对大气进入段复杂的非线性模型,文献[8]通过线性化预测模型,设计了基于约束预测控制的轨迹跟踪方法,但这种模型失配的影响会造成精度下降。文献[9]提出了一种火星大气复合进入轨迹跟踪策略,将约束多模型预测控制和干扰观测器结合,提高了着陆精度。基于非线性预测控制(nonlinear MPC, NMPC)算法[10],文献[11-12]设计了基于阻力跟踪的火星大气进入段NMPC制导律,能够在满足控制约束的条件下实现安全着陆。但其采用泰勒级数展开对未来输出进行近似预测,在模型不确定性较大情况下预测精度不高,会降低制导精度。文献[13]综合考虑了控制量约束和高度约束,基于局部线性化的NMPC和状态观测器提出了一种新的制导方案,不对模型进行简化,直接利用数值优化算法在线求解复杂非线性规划(nonlinear programming, NLP)问题的NMPC方法可以避免采用线性模型或近似预测造成的模型失配影响,具有更高的精度,但大大增加了计算的复杂度,会导致控制系统的指令延迟。
神经网络(neural network,NN)[14]是模仿大脑神经网络结构和功能而建立的算法,在航天器制导方面得到了广泛应用,如针对传统预测校正制导方法中高精度制导与快速实时解算之间的矛盾,文献[15]提出了一种基于最优制导模板的神经网络预测制导方法,提高了综合性能。文献[16]结合数值预测校正制导算法和神经网络的优点,设计了进入制导的神经网络在线预测器。近年来,由于计算机技术的迅速发展以及在多层神经网络训练方面取得的大量研究成果[17],一些学者对神经网络,尤其是深度神经网络(deep NN,DNN)在控制领域应用的兴趣在不断提高。尽管DNN特别适用于如图像识别、语音识别等感知相关的问题[18],但最近一些研究证明一些控制问题也能充分利用DNN的优势[19-20]。文献[21]以非线性肢体模型为研究基础,证明了由自动编码器堆叠而成的深度神经网络能够学习最优控制和状态的对应关系。文献[22]通过训练深度神经网络来近似表示4种不同飞行器在精确着陆场景中最优控制量,证明了利用DNN实现实时最优控制的可行性。
考虑到大气进入段复杂的非线性模型,利用NMPC方法设计的制导系统需要数值求解相当复杂的优化问题,收敛到最优解的速度较慢,而且每个制导周期的预测输出要通过对预测模型的非线性微分方程组进行数值积分得到。这些计算较为耗时,使其直接应用于在线制导比较困难。而具有强大特征学习能力的DNN利用深层非线性网络结构,能够实现复杂关系的逼近,具有快速寻找优化解的能力。因此,结合NMPC与DNN各自的优势设计制导方法是一种可行的思路。
本文针对火星大气进入参考轨迹制导问题,首先考虑模型不确定性对NMPC系统预测精度的影响,提出了一种提高系统鲁棒性的预测模型优化方法,并采用变预测时域策略改善系统性能。然后以改进的NMPC系统为制导模板,通过训练深度神经网络来实现火星智能进入制导。最后通过仿真验证了所设计方法的有效性。
1 大气进入段动力学模型
火星大气进入段的动力学方程表示为
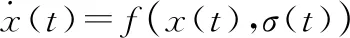
(1)
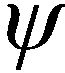
(2)
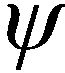
(3)
(4)
(5)
式中:μ=4.279 2×1013m3/s2为火星引力常数;m=2 802 kg为探测器质量;S=15.9 m2为探测器参考面积;CD和CL分别为气动阻力系数和升力系数,升阻比小于0.25。大气密度模型如下:
(6)
式中:ρ为高度h=r-r0处的大气密度;火星半径r0=3 396.2 km;hp为火星高度参数,取9 354 m;ρ0为火星表面的标准大气密度,取0.015 8 kg/m3。
2 制导方法设计
进入制导包括互相解耦的纵向制导和横向制导,两个通道均是将滚转角作为唯一的控制变量。纵向制导通过调整滚转角的大小来改变探测器升力在纵向平面的分量,影响纵程大小;横向制导则是通过改变滚转角的符号来改变探测器的航向,减小横程偏差。而由运动学分析可知,以能量作为自变量时,探测器的纵程由阻力加速度确定,因此轨迹跟踪制导方法通常对阻力加速度进行跟踪。
2.1 NMPC系统设计
2.1.1 NMPC系统基本框架
首先将探测器的纵向制导模型表示为如下所示的离散形式的动力学方程:
(7)
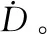
(8)
模型预测控制是一种基于模型的闭环优化控制策略,包括预测模型、滚动优化和反馈校正3个部分[23]。其主要思想是利用预测模型预测系统的未来状态量和输出值,基于有限时域在线反复优化的思想,在每一个采样时刻在线求解带有约束的二次规划或非线性规划问题,即相当于求解开环最优控制问题。每一次求解都能得到一个控制序列,但是只将第一个控制量作用于系统。然后更新系统实时状态并重复上述过程,依次滚动向前进行,最终实现闭环最优控制。
由于执行机构的限制和工程要求,探测器滚转角的调整范围限制在10°~80°,因此纵向制导动力学模型的控制输入存在约束,给控制系统设计带来一定困难。而MPC的显著优势就是可在线处理控制量和状态量约束,可以很好地改善滚转角控制饱和的现象,同时也可以对飞行路径进行约束。对于本文研究的大气进入制导问题,NMPC制导系统框图如图1所示。
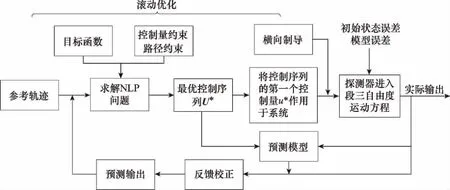
图1 非线性模型预测控制系统框图Fig.1 Block diagram of nonlinear model predictive control system
在当前时刻k,有导航系统测量得到的探测器飞行状态值x(k),构建如下形式的带约束的非线性规划问题:
(9)
定义要优化的目标函数为
(10)
优化过程需要满足以下约束条件:
cos(σmax)≤u(k+i|k)≤cos(σmin), 0≤i≤Nc-1
(11)
(12)
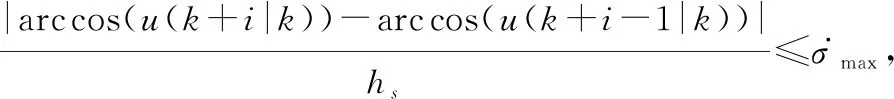
(13)
yc(k+i|k)≤yc max, 0≤i≤Np
(14)
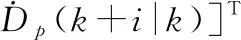
Nc和Np分别是控制时域和预测时域,通常Nc≤Np。优化问题的独立变量Uk是从k时刻起控制时域内所有时刻的控制量组成的控制序列:
Uk[uk,uk+1, …,uk+Nc-1]T
(15)
而控制时域之外的控制量大小全部等于控制时域内最后时刻优化得到的控制量,即
u(k+i|k)=u(k+Nc-1|k),Nc≤i≤Np-1
(16)


(17)
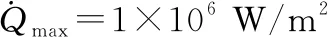
预测值yp(k+i|k)和yc(k+i|k)通过求解下面预测模型的方程得到:
(18)
式中:x(k)为当前k时刻测得的探测器实际飞行状态量,作为预测模型开始进行预测的初始状态;xp(k+i|k)为k时刻对k+i时刻状态量的预测值。
在每一个优化时刻增加对预测误差的校正环节,提高控制系统克服不确定性的能力。定义k时刻预测输出与实际输出之间的误差为

(19)
式中:yp(k|k-1)为k-1时刻对k时刻输出的预测值。以对e(k)加权的方式修正未来输出的预测:
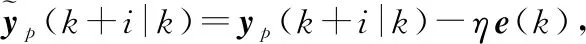
(20)

最后利用优化算法求解由式(9)和式(11)~式(14)构成的NLP问题,只将得到的优化序列的第一个最优解作用于系统,即当前k时刻的最优控制量为
(21)
由于求解出的最优控制量只包含了滚转角的大小信息,还需要通过横向制导确定滚转角的符号,得到最终的滚转角指令σ(k)。到下一时刻,根据探测器的实际飞行状态,进行对未来输出的预测和校正,重复对上述NLP问题的求解,滚动向前优化,实现闭环最优控制。
2.1.2 预测模型修正方法
由于在实际大气进入过程中存在较大的气动系数和大气密度模型误差,而预测模型式(18)没有考虑这些误差,因此计算得到的预测输出值误差较大,会降低校正环节的作用效果,使NMPC方法的鲁棒性变差。故本文从产生预测误差的源头出发,提出了一种基于误差信息估计的预测模型修正方法。首先通过设计一阶衰减记忆滤波器来获取误差估计信息。由式(2)、式(4)、式(5)和式(8)可知,气动系数和大气密度误差仅通过改变阻力加速度和升力加速度的大小对系统的输出和路径约束输出产生影响,因此将实际的阻力加速度和升力加速度与预测模型式(18)计算得到的相应量的比值作为滤波器的状态,即
(22)
式中:L(k)表示k时刻实际的升力加速度;Dp(k|k-1)和Lp(k|k-1)分别表示k-1时刻预测模型式(18)对k时刻阻力加速度和升力加速度的预测值;z*(k)为滤波器的当前状态量。则一阶衰减记忆滤波器如下所示:
z(k)=z(k-1)+(1-ε)(z*(k)-z(k-1))
(23)
式中:z(k-1)表示滤波器上一时刻的状态量;0<ε<1为增益系数。为了减小模型不确定性的影响,可适当取较大的增益系数以增强滤波器的过去状态量对当前输出值z(k)的修正作用,这里取ε=0.9。滤波器初始值z(0)取1。将滤波器的输出z(k)作为预测模型式(18)的修正因子,对阻力加速度和升力加速度的进行实时修正,即

(24)
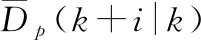
(25)
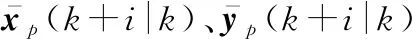
2.1.3 变预测时域策略
对大气进入制导问题分析可知,进入初始段的大气密度很小,末段探测器的速度较小。由式(4)可知,这两个阶段的阻力加速度都很小,模型误差等不确定因素对阻力加速度跟踪效果的影响不大。因此进入初始段和末段的预测时域Np可选取较小值,减小输出预测的计算量;而在探测器中间段飞行状态变化较快,阻力加速度较大,因此跟踪误差的变化比较剧烈,应选取较大的Np以提高系统的鲁棒性。故这里采用变预测时域策略,以实际输出与期望输出之间误差变化率的大小作为判断依据,合理选择不同飞行阶段预测时域的大小,提高NMPC制导系统的性能。
k时刻的预测时域Np通过下式确定:
(26)
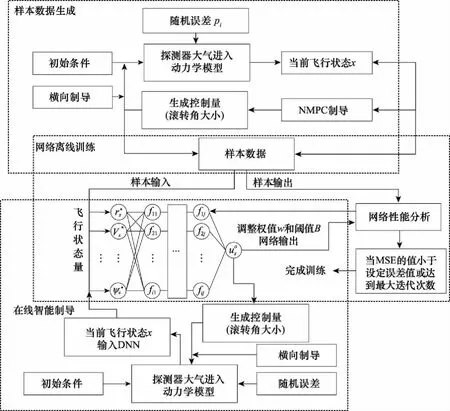
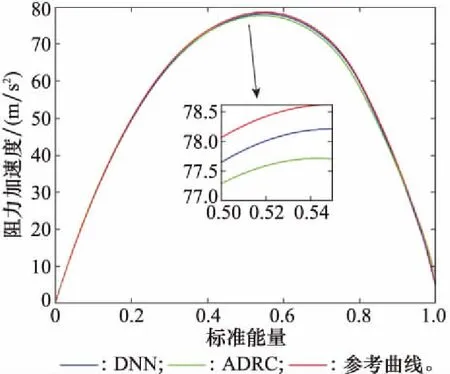
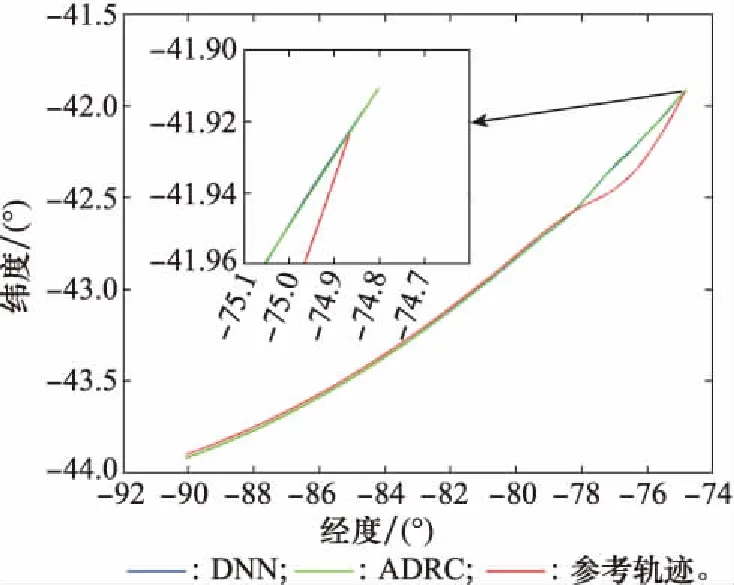
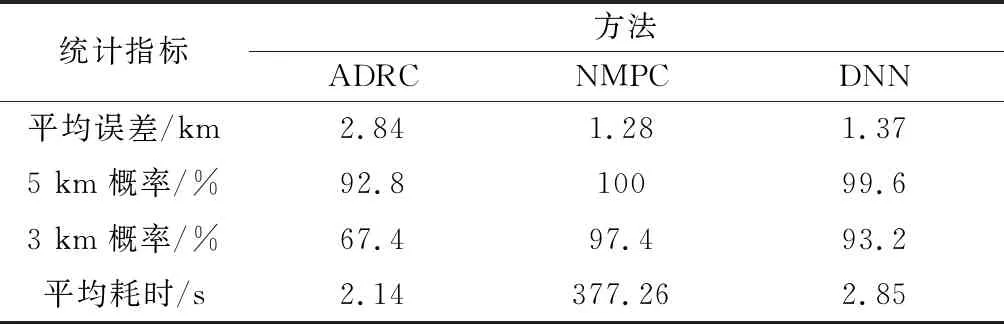
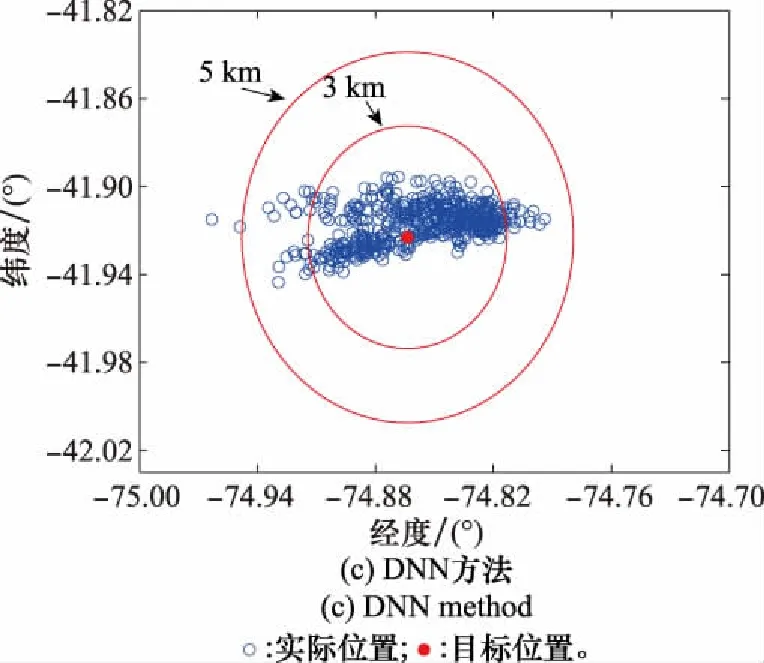
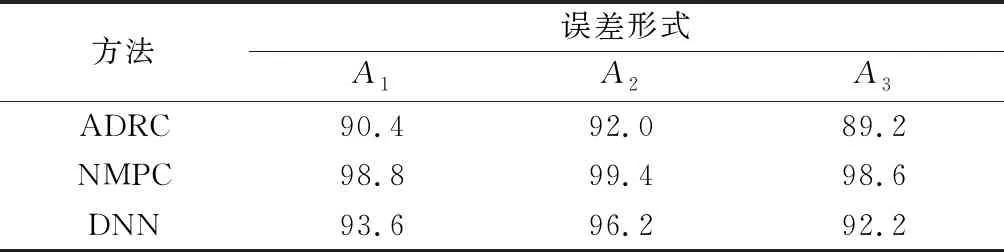
式中:k1(k)和k2(k)分别为实际阻力加速度和其一阶导数与期望值之间误差的变化率;λ1和λ2为适当的变化率阈值;预测时域N1 通过上述两种方法对NMPC系统进行改进,表1为NMPC制导系统的设计参数。 表1 NMPC制导系统参数 采用序列二次规划(sequence quadratic program, SQP)和粒子群优化(particle swarm optimization,PSO)算法相结合的混合算法求解NLP问题[24]。PSO算法在迭代初期有着较强的全局优化能力,能够在控制量的约束范围内快速收敛到一个接近全局最优解的位置,然后SQP算法将其作为优化的初始值并在该位置附近搜索,从而收敛到全局最优解。这种混合优化算法很大程度上避免了SQP算法容易产生局部最优解的问题,可以更快、更准确地找到最优解。 本文横向制导采用设置漏斗边界的方法[25]。通过滚转角翻转,调整航向角方向,将横程限制在漏斗边界内,使得到达进入段终端位置时的横程误差尽可能小。 虽然设计的NMPC制导系统能实现高精度制导,但仍然存在一些缺陷:在每一个制导周期都需要通过数值优化算法求解一个复杂的NLP问题,耗费较长时间才能迭代得到最优解;由于利用预测模型计算预测输出时要对动力学方程进行数值积分,当预测时域较大时,会带来较大的计算负担。这些问题会造成控制指令具有较大的延迟输出。为了克服这些缺陷,提高指令计算速度,本文利用深度神经网络学习NMPC系统的输入输出特性并作为制导指令生成器,实现智能进入制导。方法流程图如图2所示,包括样本数据生成、网络离线训练和在线智能制导3个步骤。 图2 智能制导方法流程图Fig.2 Flow chart of intelligent guidance method 2.2.1 样本数据生成 以上一节中设计的NMPC制导系统为制导模板,生成样本数据。数据生成的过程如下: 步骤 1设置标称进入条件I=[x0,CL,CD,ρ]T,包括初始状态x0(高度、速度、经纬度、航迹角和航向角),气动系数CL和CD以及大气密度ρ; 步骤 2引入误差项pl=[Δx0,ΔCL,ΔCD,Δρ]T,其中l=1,2,…,m,m为跟踪轨迹条数。则系统的实际进入条件为dl=I+pl; 为保证训练精度并充分发挥深层网络揭示数据内在特征的能力,这里选取m=3 000,因此样本集Q包含了大约6×107个“状态量-最优控制量”的数组对。最后将样本集Q随机划分为训练集Q1和测试集Q2,比例设置为90%和10%。 2.2.2 网络离线训练 DNN是指隐含层个数大于1的深层神经网络,其隐含层个数和每层神经元的个数对网络的特性有很大的影响,因此本文考虑不同结构网络的性能。同时为了对比,也对只有一个隐含层的浅层网络进行了训练。虽然单隐含层的神经网络只要神经元的数目足够大,就能够拟合任意精度的非线性函数,但是其对于复杂问题的学习能力有限,而且易于过度拟合,泛化能力较差。与之相比,深层神经网络通过增加隐含层个数,使网络的复杂度以指数级别提高,学习数据特征的能力更强,也具有更强的泛化能力。此外,神经元的激活函数也是影响网络性能的重要因素之一。因此隐含层和输出层分别采用了不同的激活函数进行训练。对于隐含层,线性修正单元(rectified linear unit, ReLU)函数相比于经典的sigmoid函数,除了计算量小、便于优化外,其不会发生饱和的特性能够很好地解决后者在训练深层神经网络时出现的梯度消失问题,并且降低发生过拟合的概率。故本文将ReLU函数与具有较快收敛速度的双曲正切S型函数tansig进行比较。对于输出层,采用线性传递函数purelin和函数tansig两种。 第j层的第i个神经元的输出如下所示: fij=G(wijfi-1+bij) (27) 式中:wij为权值向量,bij为该神经元对应的阈值,fi-1为上一层神经元的全部输出,G为激活函数。 训练过程就是通过误差信息的反向传播不断调整网络的权值和阈值,使式(28)所示的均方误差函数最小。 (28) 网络的训练算法采用具有动量的随机梯度下降法(stochastic gradient descent, SGD)[26],相比于传统SGD算法,可以获得更快的收敛速度并减少扰动。设置学习率η=0.001和动量因子μ=0.9,按照如下形式进行权值更新: (29) 另外,本文采用l2正则化和dropout两种深度学习中的常用技术来避免DNN容易出现模型过拟合即泛化能力差的问题[27-28]。l2正则化方法就是在目标函数中引入额外的信息来惩罚过大的权重参数,也称作权重衰减。加上l2正则项的损失函数可以表示为 (30) 式中:λ为权值衰减系数,控制正则项的大小。 dropout是指在DNN训练过程中按照一定的概率将部分神经元暂时从网络中丢弃(激活函数输出为0),减弱神经元节点间的联合适应性,尤其在数据量较大时能有效缓解过拟合的发生,增强网络泛化能力。设置节点的丢弃率为0.5。 利用归一化后的训练集Q1对不同结构的DNN进行训练。使用Xavier初始化方法[29]随机设置初始权值,能够避免训练深层网络时,后面层激活函数的输出值趋于0的问题,更有利于提高模型性能和收敛速度。权值wij服从如下的均匀分布: (31) 式中:ni和ni+1分别表示前一层和后一层神经元的个数,当神经元激活函数为ReLU函数时,β=12;激活函数为tansig函数时,β=6。网络训练的目标误差设定为1×10-6,最大迭代次数设定为5 000。当损失函数的值收敛到设定的误差范围或达到训练的最大迭代次数时,即完成网络模型的训练。利用测试集Q2中的数据对网络性能进行测试,通过多次实验,得到对样本特征学习效果相对更好的网络结构,保存其相应的网络参数,用于在线制导。 虽然文献[16]基于预测校正制导方法设计的神经网络制导器取得了不错的效果,但其局限性在于只利用较少的样本数据和传统的单层神经网络进行离线训练,对复杂非线性特征的表示能力有限,泛化能力也受到一定制约。针对这一关键问题,本文基于NMPC模板得到的海量样本数据,采用深度神经网络来增强对非线性特征的学习能力,提升网络精度的同时能够避免过拟合现象,保证网络良好的泛化能力,使其在训练集外也具有可靠性能,提高神经网络制导方法实际应用的可行性。在下一节中进行相应的仿真验证。 仿真的初始条件、进入段终端参数以及参考轨迹的设计方法参考文献[30],具体数据如表2和表3所示。生成样本数据时设置的各项误差分布范围和形式如表4所示,包括初始状态误差、气动系数以及大气密度误差,并将实际进入条件的分布范围记为A。 表2 初始状态参数 表3 终端状态参数 表4 误差参数 本节首先通过对不同结构的网络进行训练,进行深层与浅层网络对非线性关系学习效果的对比,并分析了激活函数、网络层数和神经元个数对DNN性能的影响。然后对网络的泛化能力进行了分析,最后通过与其他方法进行仿真对比,说明本文提出的制导方法的优势。 利用训练集Q1训练不同结构的网络,然后通过测试集Q2对网络进行测试,通过训练均方误差Etrain和测试均方误差Etest进行网络性能的评估。表5为深度神经网络(4个隐含层、每层32个神经元)在不同隐含层-输出层激活函数下的网络训练效果对比。 由表5结果可知,ReLU函数作为隐含层激活函数时的Etrain和Etest均明显小于tansig函数,说明ReLU函数确实更有利于DNN的训练。同时可以得到输出层为purelin时网络能取得更好的性能,因此下面进行DNN训练时均采用Relu-purelin结构的激活函数。 表5 不同激活函数的DNN训练效果 表6为不同层数和神经元个数网络的训练效果对比,其中层数指隐含层和输出层个数之和,神经元数为各隐含层的神经元个数。 表6 不同层数和神经元个数的网络训练效果 从表6可以看出,虽然浅层网络(一个隐含层和一个输出层)采用了足够多的神经元个数来提高拟合能力,但Etrain和Etest的减小并不明显,训练效果的提升较小,说明浅层网络对复杂特征的学习能力有限;在网络参数个数大致相同的情况下,深层网络的性能总是优于浅层网络,而且随着深度的增加,Etrain和Etest也基本上保持逐渐减小的趋势,这表明增大网络深度可以获得更强的非线性关系学习能力,也体现了采用深度神经网络来获得更佳学习效果的必要性。综合考虑网络复杂度和性能,这里选用具有5层16个神经元的DNN结构学习NMPC系统状态-控制量之间的非线性关系。 为了验证训练好的深度神经网络作为滚转角控制量生成器用于进入制导的有效性,首先将其与采用自抗扰控制(active disturbance rejection control, ADRC)理论设计跟踪制导律的方法[7]进行了对比,从样本集中随机选取一组实际误差条件,单次仿真结果如图3~图6所示。 图3 滚转角曲线Fig.3 Bank angle curve 图3和图4分别为滚转角变化曲线和漏斗边界,在横向制导作用下,滚转角符号进行了若干次改变,使得探测器保持在漏斗区间内飞行,保证了横程误差尽可能小。阻力加速度变化曲线如图5所示,相比ADRC方法,DNN方法对参考阻力加速度的跟踪效果更好。图6为经纬度变化曲线,由结果可看出,两种方法终端位置距离目标点的误差均小于5 km,其中ADRC方法的误差为3.49 km,而DNN方法仅为1.35 km,制导精度明显更高。 图4 漏斗边界Fig.4 Funnel boundary 图5 阻力加速度曲线Fig.5 Drag acceleration curve 图6 经纬度曲线Fig.6 Latitude and longitude curve 然后从制导精度和计算耗时两个方面考虑,通过多次仿真验证本文方法相比ADRC和NMPC方法的优势。使用不同方法进行500次蒙特卡罗打靶仿真的结果如图7所示,仿真结果统计如表7所示。 表7 仿真结果 图7 蒙特卡罗仿真结果Fig.7 Results of Monte Carlo simulation 3种方法终端位置误差在5 km范围内的概率都达到了90%以上,能够满足基本的精度要求。但相比于ADRC方法,DNN和NMPC方法的平均误差明显更小,误差在3 km范围内的概率也更高,能更好地满足高精度制导需求。DNN的制导精度虽然略低于NMPC方法,但相差很小,这表明训练好的深度神经网络很好地逼近了NMPC制导系统的特性。 表7中统计了仿真一次的平均计算时间(仿真运行环境为Windows 10,处理器为Intel Core i7-9750H 2.60 GHz)。由于每个制导周期都要通过数值优化算法求解NLP问题以及进行积分预测,NMPC方法指令计算的平均耗时最长。与NMPC方法相比,ADRC方法和DNN方法因为计算复杂度低,平均耗时与NMPC相比减少了两个数量级,能够快速在线解算指令。这说明DNN除了具备强大的非线性特性学习能力外,与NMPC制导方法相比,其主要优点是计算速度快。虽然训练过程比较耗时,但DNN一旦训练完成,网络在极短的时间内就能计算出控制量,实现实时制导。 考虑到实际火星大气过程的进入初始状态和模型误差等进入条件肯定存在与样本集不一致的情况,这就需要分析本文DNN的泛化能力。 为了更全面地对网络性能进行分析,本文考虑了实际进入条件的随机误差按照范围A分布和实际误差大小超出范围A的两种情况。 (1) 随机误差按照范围A分布。用于在线制导的DNN是基于样本数据事先离线训练好的,然而实际进入条件通常是按照范围A分布的随机情况。因此,按范围A随机生成500组误差并进行仿真,同时为更全面地说明DNN制导的性能,也与其他方法进行了对比,结果如表8所示,统计数据为终端位置误差小于5 km的概率。 表8 在范围A之内的仿真结果 (2) 随机误差大小超出范围A。尽管生成样本集时设定的范围A基本能够覆盖所有的误差情况,但由于火星大气环境存在较大的不确定性,实际进入过程的各类误差仍有可能超出该范围。所以,有必要进一步对实际进入条件在范围A之外时DNN制导方法的适应性进行分析。 为了分析不同误差情况下DNN的性能,将误差分为初始状态误差和模型误差两类,即令误差项pl=[Δx0,ΔCL,ΔCD,Δρ]T=[Δx0,Δmc]T。设置不同的误差分布形式,如下式所示: (32) 式中:A1为只考虑某一项初始状态误差超出范围A的情况;A2为只考虑某一项模型误差超出范围A的情况;A3为考虑这两种情况同时出现;Pe为超出原误差范围的百分比,这里Pe的取值为30%。在各误差情况下分别进行500次仿真,结果如表9所示,统计数据为终端位置误差小于5 km的概率。 表9 在范围A之外的仿真结果 由上述结果可知,实际进入条件在按照范围A随机选取的情况下,DNN仍然可以根据飞行状态自主生成最优控制指令,准确地将探测器导引到目标位置,误差小于5 km的概率达到了98.2%。从表9可以看出,当实际误差超出范围A时,制导精度虽然有所下降,但3种误差形式下的DNN也都能保持相对较高的性能。其中A2情况下DNN的制导精度最高,而在A1和A3情况下精度下降相对明显,尽管终端位置误差小于5 km的概率也都能在90%以上,但制导精度与NMPC方法的差距较大,相比ADRC方法的性能优势也有所降低。本节的仿真结果充分表明了当实际进入条件在生成样本集的误差范围内随机分布时,DNN能够近似得到最优解,一定程度上说明DNN通过深层次的非线性网络结构成功学习了NMPC系统的特征,体现出了良好的泛化能力。但DNN在不确定扰动的大小超出一定范围尤其是初始状态误差较大时,很难保持与NMPC方法相似的性能,和传统方法相比也已不具有明显的优越性,这也是本文方法的局限性所在。虽然可以通过增大样本覆盖区域进行改善,但无疑提高了网络训练的难度和时间代价。 综合以上分析可知,本文提出的DNN制导方法不仅很好地兼顾了制导精度和计算耗时两个方面的需求,实现高精度制导的同时具有很快的指令计算速度,而且能够较好地适应实际进入条件存在各类不确定误差的情况,一定程度上保证了其用于在线精确制导的可行性。虽然由于网络训练本身的局限性,在误差过大的情况下该方法的性能优势会有所下降,但仍然能够满足制导精度需求。 本文针对火星大气进入在线精确制导问题,提出了一种以非线性模型预测控制系统为制导模板,利用深度神经网络实现智能在线制导的策略。首先通过提出的基于误差信息估计的预测模型修正方法和变预测时域策略,对NMPC系统进行改进,增强了系统对模型误差的鲁棒性,改善了系统性能。然后利用DNN学习NMPC制导系统的特性,在每一个制导周期代替数值优化求解复杂NLP问题以及积分求解预测输出的过程,很大程度上克服了NMPC方法求解复杂度高的缺点,减小了指令解算时间。最后,对不同结构网络的学习性能进行了比较,并通过对DNN泛化能力的分析进一步验证了方法的可行性,同时指出了局限性。仿真结果验证了DNN方法相比其它方法在制导精度和计算速度上的优势,表明本文提出的方法能够实现探测器大气进入段高精度在线智能制导。
2.2 基于NMPC的深度神经网络制导

3 仿真结果及分析



3.1 网络结构的影响

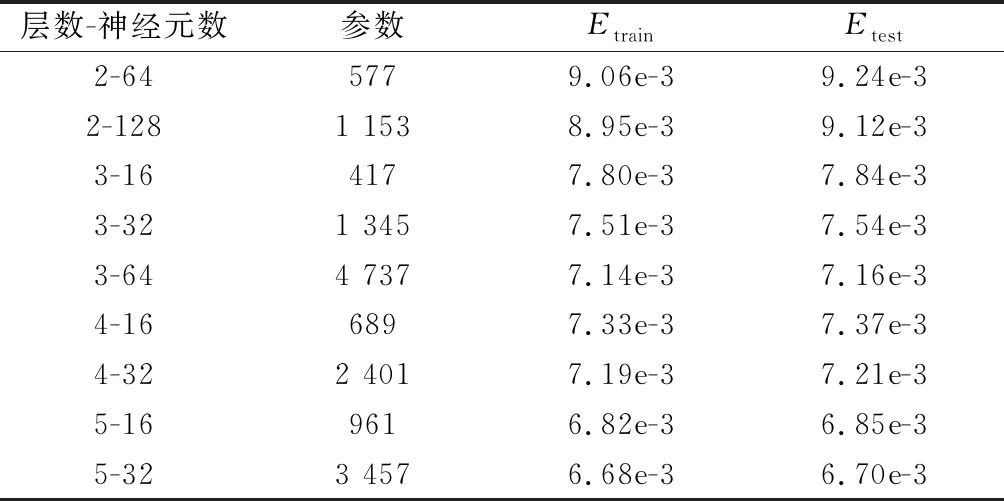
3.2 不同制导方法的比较



3.3 网络泛化能力的分析

4 结 论

