稀疏场景下SAR方位向随机丢失数据的迭代成像算法
杨卫星, 朱岱寅,*
(1. 南京航空航天大学电子信息工程学院, 江苏 南京 211106;2. 南京航空航天大学雷达成像与微波光子技术教育部重点实验室, 江苏 南京 211106)
0 引 言
合成孔径雷达(synthetic aperture radar,SAR)是一种重要的遥感观测技术,具有二维高分辨成像、全天时以及全天候的特点[1-3]。SAR在距离向发射大带宽信号时利用脉冲压缩技术实现高分辨成像,方位向利用相干积累模拟合成大的虚拟孔径实现方位向的高分辨成像。一般的,为了实现二维高分辨成像,雷达需要在机载或者星载平台沿着方位向飞行一段时间,在超高分辨的情况下飞行时间可达到几十秒。雷达在飞行过程中,容易受到干扰从而导致飞行数据缺失。对于SAR雷达二维成像来说,方位向的数据比距离向更容易缺失。根据缺失数据的形状,可以分为周期性的缺失和随机性的缺失[4-5]。周期性的缺失数据主要存在于特定的雷达工作模式中:如间断SAR成像模式[6]。而随机性的数据缺失较为常见,比如雷达飞行受到随机干扰时,容易产生随机的数据缺失。因此,SAR缺失数据成像问题是提高SAR成像质量必须要解决的问题。
针对缺失数据的SAR成像问题,缺失的部分设置为0后,采用基于傅里叶变换的成像算法,会导致点扩散函数不再是理想的sinc函数形状,出现模糊和目标能量分散的情况,严重降低成像的质量。为了克服SAR缺失数据后成像模糊、虚假目标以及目标能量分散的问题,人们已经提出了大量的解决办法。文献[7]提出了采用插值的方法补全缺失的部分数据,插值方法需要存在大段连续的数据块并且缺失的数据量较小才能保证补全的偏差较小,在缺失数据量大以及随机缺失的情况下并不能采用插值的方法恢复补全缺失的数据。现代谱分析方法能够对时间序列进行预测和外推,可以用来提高SAR缺失数据成像的质量消除虚假目标。文献[8]提出采用自回归(auto regressive,AR)模型的近似最大似然预测器的方法估计恢复缺失的数据,这一类基于AR模型的算法严重依赖模型参数,对于缺失数据的SAR回波信号,通常很难确定模型参数,导致该类算法恢复重建成像的质量很差。
基于参数模型补全SAR缺失数据成像的算法存在严重不足,人们提出了采用基于非参数化自适应滤波器的算法用来解决SAR缺失数据成像的问题。该类非参数化的算法主要分成两种:缺损数据幅度-相位估计(gapped-data amplitude and phase estimation,GAPES)算法和数据丢失的迭代自适应算法(missing data iterative adaptive algorithm,MIAA)。其中GAPES算法利用最小均方误差准则对缺失的数据进行估计,对模型误差和噪声的补偿有较好的准确性,但是计算负担较大[9-10]。MIAA相较于GAPES算法计算负担较小,由于MIAA基于加权最小二乘准则对缺失的数据进行估计,在缺失数据量大的情况下也有优越的性能[11-12]。由于SAR回波信号并非严格的单频信号叠加,而且存在运动误差和距离徙动,利用非参数谱估计的方法恢复缺失的SAR数据,并不能有效地解决模糊和虚假目标的问题。
近些年来,稀疏优化方法得到了广泛的研究。当SAR的观测场景稀疏时,可以利用稀疏优化理论对SAR回波信号进行重构成像[13-14]。稀疏优化方法中的压缩感知理论表明,某一信号在一定变换域稀疏的条件下,可以对低于奈奎斯特采样频率获取的数据利用一定的优化算法进行重构恢复出原始的信号。基于压缩感知理论的SAR重建成像方法,不仅可以针对完整的SAR数据成像还可以针对缺失的SAR数据进行成像。SAR雷达系统是按照奈奎斯特采样定理录取数据,当SAR回波存在数据缺失时,已经不满足奈奎斯特采样理论,因此可以利用压缩感知理论解决SAR缺数数据成像的问题。文献[15]中考虑到SAR成像原理,提出了采用精确观测模型的SAR成像理论框架,利用正交匹配追踪方法重建成像,明显提高了SAR成像的质量。文献[16]提出了利用l1/2范数约束优化的重建算法,在更少数据量的情况下也能有效地重建成像。
直接采用精确观测模型的压缩感知SAR成像算法存在计算量大的问题,适合小数据量的SAR重建成像。在大数据量的SAR成像时一般采用分块重建成像[17]。文献[18]提出了采用近似观测模型的稀疏SAR成像框架,该理论框架可以针对大数据量的SAR回波直接重构成像,是目前可以实际应用的稀疏SAR成像理论框架。并且在文献[18]中利用迭代收缩阈值算法,结合近似SAR观测模型对稀疏场景的SAR回波数据进行重构成像,计算内存消耗明显减小而且得到了更优的重建成像质量。目前应用近似观测模型的SAR成像框架,大部分采用迭代软阈值收缩(iterative soft thresholding,IST)优化重构算法以及相关的改进算法,该类重构算法是一种有偏的算法,存在着一定的重建偏差[19]。
针对目前各类SAR缺失数据成像方法的不足,本文利用压缩感知理论对缺失部分数据的稀疏观测场景的SAR原始回波信号进行重构成像。本文主要针对稀疏SAR观测场景的原始回波信号方位向上任意缺失数据成像问题展开研究。本文利用求解基追踪降噪问题的新迭代重建算法,解决了压缩感知SAR重建成像目标幅度误差较大的问题。结合SAR回波近似观测模型,本文提出的算法适合方位向上缺失任意数据的稀疏观测场景大尺寸SAR回波数据矩阵的重建成像。利用了“方位向-距离向”解耦算子,有效地减小了计算量和内存消耗。相比于迭代软阈值收缩重建算法,本文提出的算法明显减小了重建误差,在SAR方位向数据缺失量较大的情况下也能有效地重构成像。
针对SAR回波数据方位向任意缺失部分数据成像的问题,利用SAR回波近似观测模型,转化为求解稀疏优化解的问题,提出了新型误差较小的迭代重建算法。受新的高精度求解l1范数约束优化问题算法的启发,本文将该方法推广到稀疏SAR成像问题上,有效地解决了SAR回波数据方位向任意缺失部分数据成像的问题。
1 基于近似观测模型方位向缺失数据的SAR成像框架
当SAR原始回波数据不完整或者丢失部分数据时,压缩感知SAR成像方法是一种提高SAR成像质量的优越方法。应用压缩感知理论来实现SAR成像,其中最关键的部分是建立稀疏观测的线性方程组。相比较于精确观测模型,近似观测模型的方法内存占用量低、计算负担小,更适合基于原始回波数据的SAR重建成像。SAR近似观测模型框架主要是利用方位-距离向解耦算子降低内存占用[20-23]。方位-距离向解耦算子就是把传统的SAR成像算法用算子的形式表示出来。目前常用的方位-距离向解耦算子有很多种,如距离-多普勒解耦算子、Chirp-Scaling解耦算子等。本文为了避免SAR成像距离徙动校正时插值运算,选择利用Chirp-Scaling解耦算子构建近似观测模型。方位-距离向解耦算子主要包括两部分:SAR原始回波数据生成算子和SAR成像算子。为了方便表示,一些矩阵算子的定义如表1所示。根据Chirp-Scaling SAR成像算法原理[24-25],方位-距离向解耦算子中成像算子可以表示为

表1 矩阵算子定义
(1)
式中:⊙表示为矩阵的Hadamard积。
SAR原始数据生成算子为
(2)
式中:(·)*表示矩阵共轭操作。
利用Chirp-Scaling方位-距离向解耦算子,可以构造方位向缺失任意数据的基于SAR近似观测模型的线性方程组。
令X为观测场景的二维复数图像矩阵,Y为方位向任意缺失数据的SAR二维原始回波数据矩阵,则根据方位-距离向解耦算子可以得到如下近似方程:
Y≈ΘaGCS(X)
(3)
式中:Θa表示SAR方位向任意缺失数据的采样矩阵。为了得到观测场景的二维复图像X,可以通过求解如下l1范数约束优化问题:
(4)
式中:λ为正则项参数。式(3)就是基于SAR近似观测模型的方位向缺失任意数据的线性方程组。通过求解式(4)就可以得到观测场景的二维图像。目前求解方法主要是IST算法及其相关的改进算法,该类算法存在较大的偏差,不利于目标检测识别等SAR图像处理。
2 改进的迭代重建算法
考虑到求解l1范数约束优化问题的一般形式为
(5)
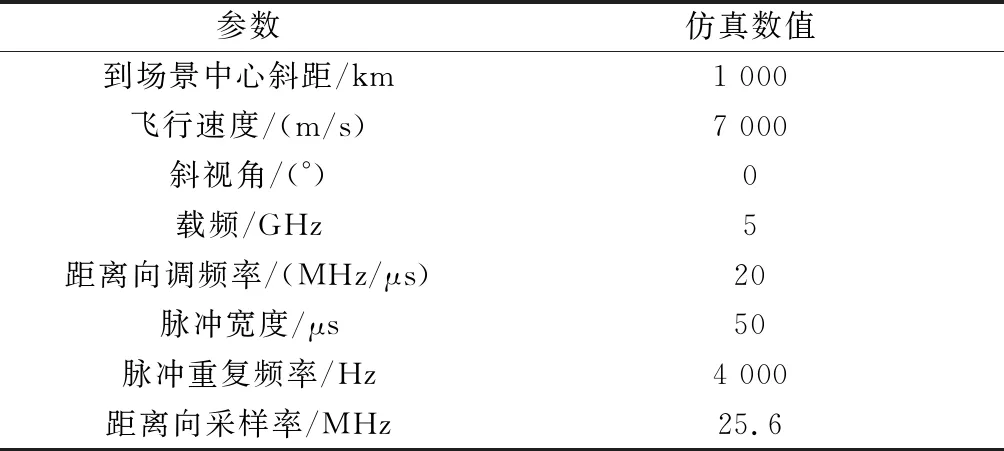
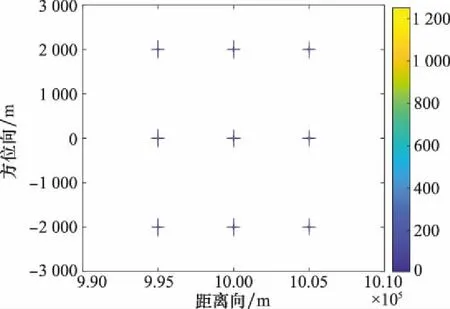
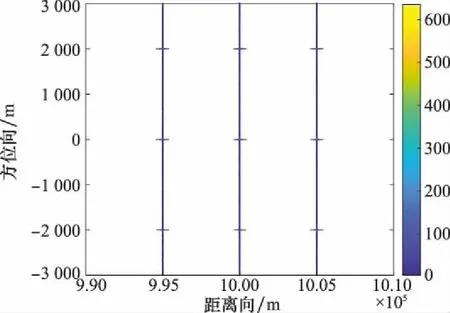
式中:x∈Rn为待重建的稀疏信号向量;y∈Rm为压缩观测信号向量;Φ∈Rm×n(m 为了求解式(5),可以利用如下的迭代计算方案[26-27]: (6) 式中:Tλ(·)为软阈值函数。该迭代计算过程简单且容易实现,只涉及矩阵向量乘法运算,因此被广泛应用于压缩感知问题的求解。阈值收缩算子使其收敛于稀疏解并且消除噪声。因此,该迭代计算对噪声具有鲁棒性。 在此迭代过程的基础上,文献[28]将其推广成如下的迭代形式: (7) 式中:Φ+表示广义逆矩阵。该迭代方法不仅可以提高收敛速度而且可以应用于病态方程的求解。然而,在计算广义逆矩阵Φ+时需要矩阵的奇异值分解,当矩阵尺度较大时计算复杂而且计算速度慢。为了降低计算复杂度、提高计算速度,在文献[29]中经过扩展,提出了如下的高精度的迭代方法: (8) 式中:μ0=V0v0,V0=ΦT,k=0,1,…。 式(8)所示的迭代过程只涉及到矩阵-向量相乘的运算,避免了矩阵-矩阵相乘和奇异值分解操作,在大尺寸数据矩阵下仍然能保持较好的性能,并且相比式(6)所示的计算方法有更高的重建精度。 受式(8)迭代计算过程的启发,结合SAR近似观测模型框架,提出了如下求解SAR方位向任意缺失数据的迭代重建方法。 输入:方位向缺失数据的原始回波信号Y,方位向缺失数据的采样矩阵Θa,最大迭代次数Imax, 方位向-距离向解耦算子ICS(·)和GCS(·) 初始化:X0,V0,M0,k=0 迭代计算:Whilek Vk+1=Vk+Y-ΘaGCS(Xk) ΔR=ΘaGCS(Μk) Xk+1=Tλ(Μk+1) k=k+1 End 本文所提算法中的阈值函数可以选择软阈值函数,具体的阈值参数根据SAR观测场景图像的稀疏程度设置。由于SAR回波数据和图像数据都存储于二维矩阵中,因此该算法的迭代计算过程涉及到矩阵-矩阵相乘还有近似观测模型的计算算子。假设二维回波矩阵的大小为M×N,迭代计算的输入、输出只需要存储这几个矩阵,内存占用为O(MN),距离-方位向解耦算子计算时的内存占用为O(MNlog2(MN))。因此,本文提出的算法与传统迭代收缩阈值算法计算量同阶。此外,该迭代重建方法是一种高精度的方法,能够有效减少重建偏差。下面通过点目标仿真数据处理和真实观测的SAR回波数据处理,证明该方法在消除SAR方位向缺失任意数据时降低成像虚假目标、减小方位向目标模糊以及提高成像质量方面的有效性。 在本节中,通过点目标仿真的回波数据和星载SAR雷达实测的回波数据处理,证明本文提出方法在消除缺失数据引起的SAR方位向目标模糊和能量分散、提高目标成像聚焦质量等方面的有效性。在实验分析中和传统的迭代软阈值收缩重建方法进行对比,进一步证明本文提出方法在减少目标重建误差、提高目标背景比等方面的优越性。本文所有的实验都在笔记本电脑上(i5-7300HQ CPU @ 2.50 GHz with 16GB of RAM)完成,所有程序代码都通过MATLAB 2018a编程实现。 为了证明本文所提方法的优越性,首先利用点目标仿真生成的理想SAR回波数据,然后,利用本文提出的算法进行点目标聚焦成像处理。仿真实验中雷达系统的主要参数如表2所示。 表2 雷达系统仿真参数 假设雷达观测场景中存在9个点目标,每个点目标具有相同的散射系数,点目标的分布如图1所示,按照仿真参数设置,在没有添加噪声的理想情况下生成大小为4 096×4 096的二维SAR回波数据矩阵。SAR回波数据的方位向按照随机缺失的形式丢失部分数据,在缺失率为50%时回波数据的示意图如图2所示。对于方位向全孔径的数据采用Chirp-Scaling算法的成像结果如图3所示。对于缺失的部分数据设置为0,利用经典的Chirp-Scaling算法的成像结果如图4所示。可见SAR方位向缺失任意数据会造成目标在方位向产生混叠模糊,目标能量出现分散,严重降低成像的质量,影响真实目标的分辨与识别。 图1 点目标分布示意图Fig.1 Schematic diagram of point targets distribution 图2 方位向任意缺失50%数据的示意图Fig.2 Schematic diagram of randomly missing 50% data in azimuth 图3 方位向全孔径数据时Chirp-Scaling算法结果Fig.3 Results of Chirp-Scaling algorithm for azimuth full aperture data 图4 方位向任意缺失50%数据时Chirp-Scaling算法结果Fig.4 Result of Chirp-Scaling algorithm with randomly missing 50% data in azimuth 图5是经过10次迭代,IST算法的重建成像结果。由图5可知,IST算法能够较好地消除方位向缺失任意数据引起的目标模糊和能量分散。图6是方位向缺失率为50%的时候,利用本文所提算法经过10次迭代重建的结果。由图6可以看出经过本文提出算法的迭代过程,虚假和模糊的目标已经消除,真实目标得到了有效重建并且重建的位置也正确,目标的旁瓣明显减少,目标的能量大大提高,成像的质量明显提高。相比较于IST算法的重建结果,本文算法的重建结果目标幅度更接近全采样数据时Chirp-Scaling算法的成像结果。 图5 方位向任意缺失50%数据时IST算法的重建结果Fig.5 Reconstructed result of IST algorithm when randomly missing 50% data in azimuth 图6 方位向任意缺失50%数据时本文所提出算法的重建结果Fig.6 Reconstructed result of the proposed algorithm when randomly missing 50% data in azimuth 为了比较每个点目标的重建误差,定义均方误差计算形式如下: (9) 表3 方位向缺失率为25%和50%时9个点目标区域中两种重建算法的均方误差 为了进一步证明本文提出算法的优势,下面通过星载SAR录取的真实观测场景的回波数据处理来论证本文提出算法的优越性。本文所选取的SAR数据是加拿大航天局发射的RADARSAT-1卫星传回的部分数据。该卫星系统的雷达参数在文献[30]中有详细说明。具体来说,本文比较了经典的Chirp-Scaling算法、迭代软阈值收缩重建算法以及本文提出的算法在方位向不同缺失率下重建成像的结果,详细说明了本文算法的优势。 首先,选择经典的温哥华英吉利海湾中几艘舰船目标的回波数据进行成像处理。数据块的大小为2 048×2 048,在数据块的方位向采用随机丢失的方式丢失部分数据。该观测场景中主要是几艘舰船目标,满足算法的稀疏性要求。完整采样数据的Chirp-Scaling算法的成像结果如图7所示。 图7 方位向全孔径数据的Chirp-Scaling算法的成像结果Fig.7 Imaging result of Chirp-Scaling algorithm for azimuth full aperture data 其次,为表明本文提出算法的优势,比较了在方位向随机缺失数据量较大时候的重建计算结果。当SAR方位向任意缺失50%数据时候,缺失的部分数据设置为0,采用Chirp-Scaling算法的计算结果如图8所示。当SAR方位向缺失数据量大的时候,方位向的目标混叠和能量分散更加严重,缺失数据的部分设置为0以后采用Chirp-Scaling算法的成像结果进一步恶化。 图8 方位向任意缺失50%数据时Chirp-Scaling算法成像结果Fig.8 Imaging result of chirp-scaling algorithm when azimuth randomly missing 50% data 当采用本文的算法经过50次迭代计算重建的结果如图9所示。当采用IST算法,经过50次迭代计算的计算结果如图10所示。对比图8和图9的结果,在方位向存在大数据量缺失的情况时,本文提出的算法也能有效地消除目标模糊和目标能量分散,使得真实的舰船目标聚焦的能量更加集中,减少了目标模糊混叠,提高了成像质量。对比本文所提出算法和IST重建算法的结果,两种算法在大数据量缺失的情况都能有效地消除目标模糊,使得真实舰船目标聚焦的能量更加集中,减少了目标混叠,提高了成像的质量。 图9 方位向任意缺失50%数据时本文算法的成像结果Fig.9 Imaging result of the proposed algorithm when azimuth randomly missing 50% data 图10 方位向任意缺失50%数据时IST算法的成像结果Fig.10 Imaging result of IST algorithm when azimuth randomly missing 50% data 为了进一步验证本文提出算法的优势,下面通过计算目标区域的目标背景比(target to background ratio,TBR)来证明本文提出算法的优越性。具体的目标背景比的定义[31]如下: (10) 式中:T表示目标区域;B表示背景区域;NB表示背景区域的像素点个数。目标背景比表示目标相对于周围背景的突出程度,该指标反应了算法提升目标背景比的能力。目标背景比越大,背景噪声的抑制能力越强,重建的目标质量越好。 在方位向缺失率分别为25%和50%两种情况下,本文提出算法和IST重建算法计算的结果中6艘舰船目标区域的目标背景比如表4所示。对比表4中目标背景比的大小可以发现,本文提出的算法和IST重建算法能够明显地提高6艘舰船目标区域的目标背景比,本文提出的算法比IST算法提升目标背景比明显,6艘舰船目标区域的目标背景比更大。因此,本文提出的算法有着更优的性能。 表4 本文算法和IST重建算法中6艘舰船目标区域的目标背景比 为了比较重建图像中重建目标幅度的误差,下面通过均方误差比较进一步表明本文提出算法的优势。依据式(9)所示的均方误差计算方法,本文提出的算法和经典的IST重建图像中,6艘舰船所在的目标区域的均方误差如表5所示。通过分析表中数据可以发现,随着数据缺失量地增加,重建目标幅度的均方误差增大,但是本文提出算法的重建目标的均方误差明显小于IST算法重建目标的均方误差。同时,在方位向数据缺失率较大的时候,本文提出的算法也能保持较高的重建精度,因此通过均方误差比较,表明本文所提出的算法是一种针对SAR方位向丢失任意数据的高精度重建算法。 表5 本文算法和IST重建算法中六艘舰船目标的均方误差 SAR方位向数据缺失问题是SAR成像方法设计中必须要面临的问题。本文针对稀疏观测场景中SAR回波信号方位向缺失任意部分数据的成像问题展开分析,利用SAR回波信号近似观测模型构建了求解l1范数问题的优化模型。分析了传统迭代收缩阈值重建算法存在较大重建偏差的缺点,提出了新的高精度迭代优化重建算法。该算法利用了方位向-距离向解耦算子有效解决了SAR成像重建过程中内存消耗巨大和计算过程复杂的问题。和传统的Chirp-Scaling算法比较,该算法有效消除了SAR方位向缺失任意数据引起的目标混叠模糊和能量分散问题。和经典的迭代软阈值收缩优化重建算法相比,该算法能够保证目标的幅度高精确度重建,进一步的提高了观测目标区域的目标背景比。稀疏观测场景的点目标仿真回波数据处理以及RADARSAT-1雷达舰船目标的真实回波信号数据处理都有效证明了本文提出算法的优越性。在数据丢失率较大的情况下本文提出的算法也有效地实现观测目标的重建成像,并且能够保持较高的重建精确性和较高的目标背景比,提高了SAR目标的聚焦成像质量。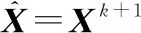
3 实验结果
3.1 点目标仿真实验


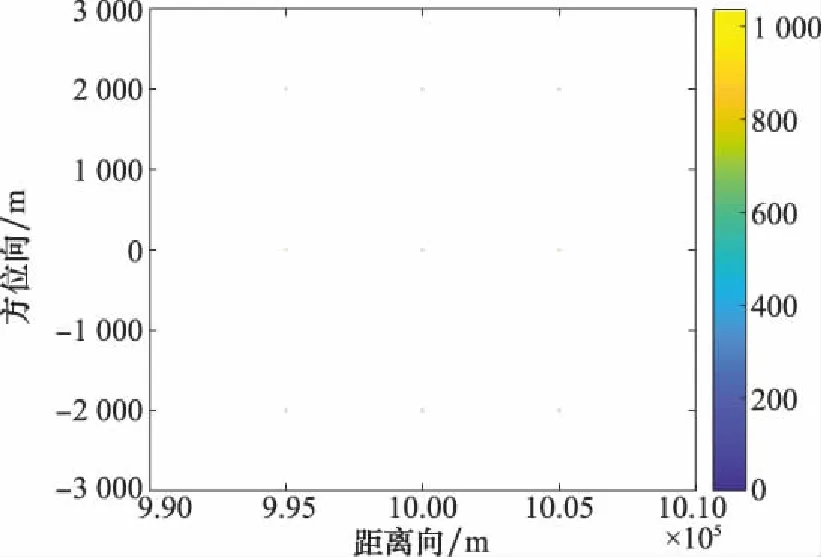
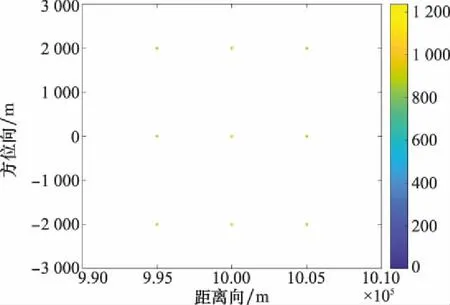
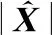

3.2 实测数据处理实验



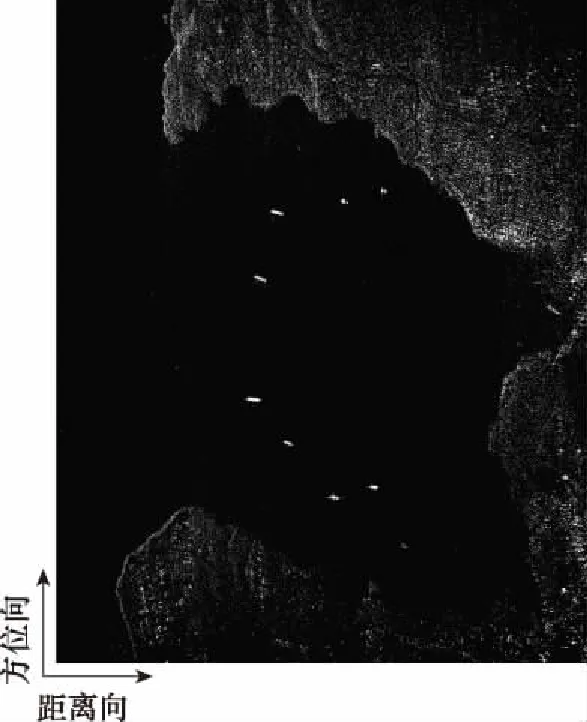


4 结 论

