含多分布式超级电容的直流微电网功率平滑协调控制方法

刘海涛，李 蕊，孙丽敬，徐旖旎，熊 雄，吴 鸣

（国网上海能源互联网研究院有限公司，上海 201213）

在以同步发电机为主的含高比例新能源接入的低惯量交直流微电网（如偏远地区、岛屿与直流舰船等独立供电系统）、基于混合储能的电动汽车直流供电系统，或直流微电网通过双向DC-AC变流器接入弱交流系统等应用场景中，高比例新能源及负荷的快速、大功率波动是此类直流微电网稳定运行控制面临的主要挑战[1-3]。利用功率型储能系统，如超级电容和飞轮储能等，提升这类直流系统的等效惯量，是有效应对功率冲击和平滑主电源输出功率[4-6]的可行方案之一。本文主要关注如何应用超级电容系统进行直流微电网暂态功率平滑以及等效惯量的提升。

针对简单微电网或容量较小的系统，可以配置集中式超级电容。一类简单的控制方法是直接对功率扰动或主电源输出功率进行量测，然后通过频率分频器进行扰动功率分频处理，最后利用超级电容系统平滑高频分量[7-8]。针对基于混合储能系统的直流微电网多尺度功率平滑控制，文献[9]提出基于虚拟电阻和电容混合参数的下垂控制策略，利用虚拟电阻与电容参数实现了多类型储能间的分频段功率平滑。上述方法要么采用了集中控制器，要么针对一个集中超级电容系统进行了讨论，若集中控制器或集中式超级电容发生单点故障，则容易降低功率平滑系统的可靠性。

为进一步提高功率平滑系统的可靠性，可采用多分布式超级电容。针对含多分布式储能的交直流混合微电网综合惯量提升与功率平滑控制，文献[10]在就地控制层利用快速通信传递交流频率和直流电压至直流微电网和交流微电网内的混合储能控制系统，采用公共就地惯量支撑控制环节得到电流参考值，然后经分频处理后将高频分量作为超级电容内环电流参考值，以平抑高频扰动。文献[11]中在双极性直流母线上分别接入超级电容且采用下垂控制实现了超级电容的功率平滑控制，同时依靠直流母线上的电压平衡器和电池对双极性直流电压的调整完成两组超级电容之间协调配合。上述方法利用通信或辅助设备实现多超级电容的协调控制，但通信故障或延时以及所依赖的辅助设备的故障均会严重影响系统暂态功率平滑控制性能与超级电容的协调配合。为此，文献[12-14]提出基于虚拟电容参数的超级电容系统下垂控制策略，使超级电容与蓄电池具备不同暂态特性的输出阻抗，从而令超级电容平抑高频分量、蓄电池承担低频分量。相比文献[9]，文献[12-14]指出当系统内并入多个超级电容系统时，可根据超级电容不同的电容量或额定容量的比例进行暂态功率的分配，进而实现协调控制，然而在其所提控制策略下这种分配原则忽略了超级电容剩余容量对暂态功率支撑的影响。如果某个超级电容系统的剩余容量较低，而其电容量或额定容量较大，若根据文献[12-14]的思路，则暂态功率平滑过程中该超级电容将存在放电受限的可能，从而影响多分布式超级电容间的协调配合，所以如何改善超级电容间的暂态功率分配是本文的关注点之一。

上述文献还存在一个问题，就是现有的超级电容控制方法均将暂态功率平滑与电容电压恢复控制进行解耦，通常在暂态功率平滑控制过程结束后，再实施二次电压恢复控制。如文献[9，13]通过控制带宽设计将超级电容系统的二次电压恢复控制与暂态功率平滑控制进行解耦，在功率平滑结束后使得电容电压恢复至额定值。文献[15]通过切换控制特性对超级电容进行充放电，维持超级电容SOC在30%～70%区间内。以上方法对超级电容电压的控制与功率平滑的控制均需要两个控制环节得以完成，能否简化超级电容控制系统设计，仅通过单一控制环节使得超级电容在完成暂态功率平滑的同时便实现电容电压的控制值得研究

为此，本文提出一种分布式超级电容功率平滑的协调控制方法，该方法的创新性在于：①每个分布式超级电容就地测量直流母线电压，然后通过相应DC-DC控制其自身超级电容电压快速跟踪直流母线电压，同时实现暂态功率平滑与电容电压的控制，且具备较好的即插即用控制特性；②基于上述控制，推导了超级电容的等效惯量表达式，并提出了按超级电容间最大惯量比进行等效惯量分配的原则，使超级电容间能够时刻按照期望比例进行暂态功率分配；③建立了系统的数学模型，讨论了电容电压与系统参数对超级电容功率平滑的影响，并通过模型的降阶，制定了超级电容电压参考值的设计方法，使多分布式超级电容能够满足系统的功率平滑需求，且能够实现超级电容间的协调配合。

1 系统结构

含多个分布式超级电容系统接入时的直流微电网结构如图1（a）所示，该系统中主要包含三类单元：平衡单元、功率单元及平滑单元，图中标号‘i’代表平滑单元的标号。对于“并网型”直流微电网来说，若交流侧为大电网或交流微电网，则可通过双向DC-AC变流器控制直流母线电压稳定；对于独立型直流微电网，则可通过电池储能系统和相应双向DC-DC变流器进行直流母线电压控制，上述单元均可称之为平衡单元，亦即主电源。直流微电网内采用最大功率点跟踪MPPT（maximum power point tracking）控制的风/光等新能源发电单元、采用功率控制模式的可控型分布式电源，以及负荷等，均可看作功率单元。

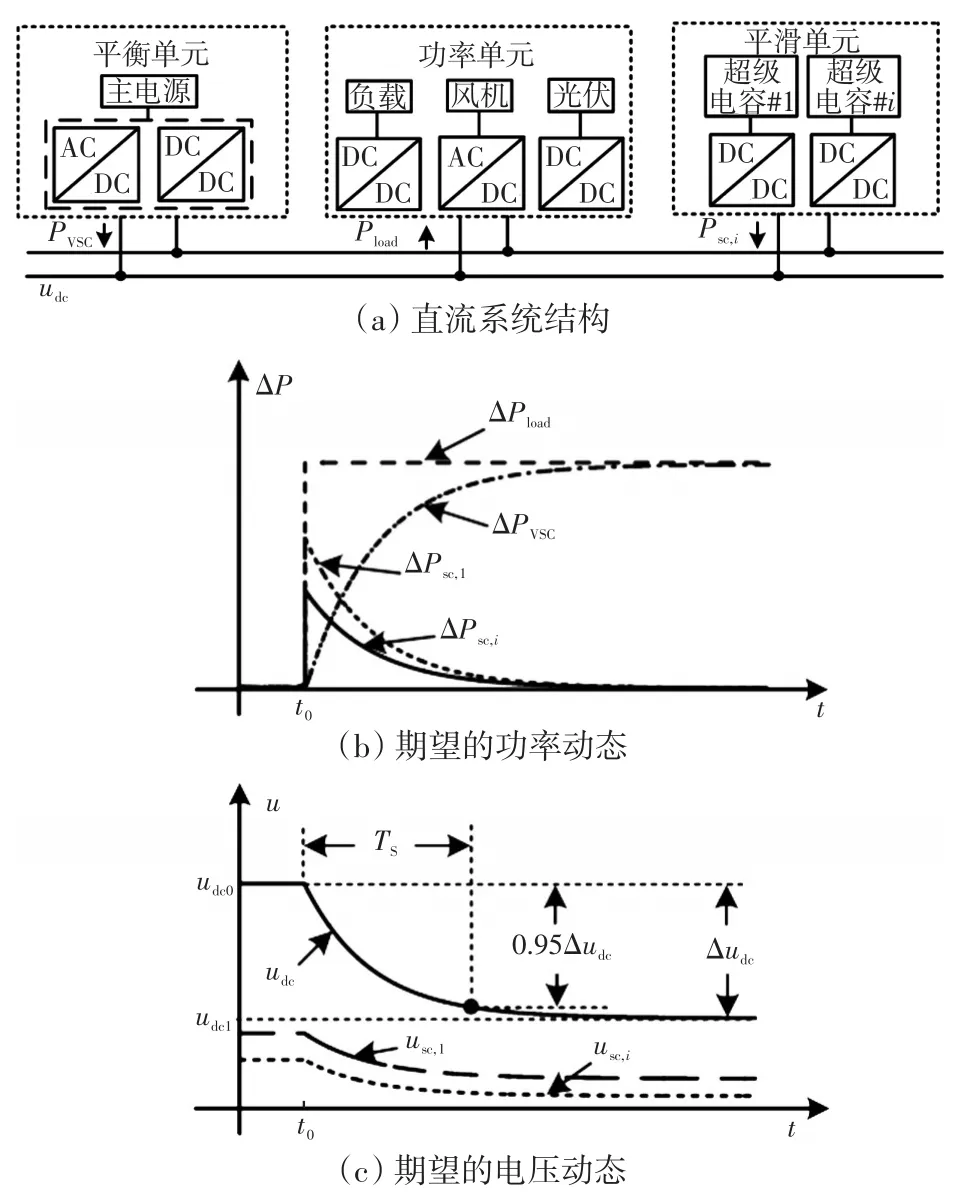
图1 直流微电网结构示意以及期望的动态响应Fig.1 Schematic of DC microgrid structure and expected dynamic response

图1中：PVSC为平衡单元的输出功率；Pload为功率单元的功率；Psc,i为第i个平滑单元的功率输出；udc为直流母线电压；usc,i为第i个超级电容的电压；udc0与udc1为扰动前、后的稳态直流电压；“Δ”为相应的变化量。当系统在t0时刻发生功率扰动ΔPload时，超级电容快速响应，各分布式超级电容功率输出分别为ΔPsc,1、ΔPsc,i，平衡单元的功率输出ΔPVSC将平滑过渡到稳态，如图1（b）所示。直流母线电压与各分布式超级电容电压动态响应见图1（c）。如何通过对超级电容电压的控制实现暂态功率平滑，超级电容电压应运行在什么水平，以及多分布式超级电容系统如何合理地分配该扰动功率是值得深入讨论的。为便于定量分析，本文定义暂态过程中的调节时间Ts（到达暂态响应终值的95%的时间）为平滑时间，该时间越长，表征超级电容的等效惯量越大，平滑能力越强，反之越弱。如果要求Ts达到某一值，如何根据该需求定量化地设计系统关键的控制参数来满足系统的平滑需求以及实现超级电容间的协调控制，便是后续要讨论的问题。

2 功率平衡单元与超级电容控制方法

本文提出的直流微电网功率平衡单元与超级电容系统整体控制结构如图2所示。其中平衡单元控制直流电压，本文以双向DC-AC变流器为例进行分析；超级电容系统的基本控制目标是实现暂态功率平滑以及自身电容电压的控制。参数设计旨在根据系统平滑需求Ts设计平衡单元与超级电容的关键控制参数，以满足系统的平滑需求，且实现多超级电容间的协调控制。下面将详细阐述平衡单元与超级电容的控制。

2.1 功率平衡单元控制方法

一般而言，功率平衡单元控制直流母线电压主要可以分为恒定直流电压控制与下垂控制。在本文中功率平衡单元采用直流电压下垂控制，主要是考虑到当多个功率平衡单元接入时，下垂控制可自动实现多平衡单元间的协调控制[16-17]。更重要的是，工作在下垂控制下的平衡单元能和平滑单元更好地分配不同频段的扰动功率[9，12-14]，同时下垂控制也能提供给直流系统一定的惯量[18]，能和超级电容协调配合共同平滑直流微电网内的暂态功率扰动。以工作在直流电压下垂控制的VSC为例，其基本的控制框图如图2所示。

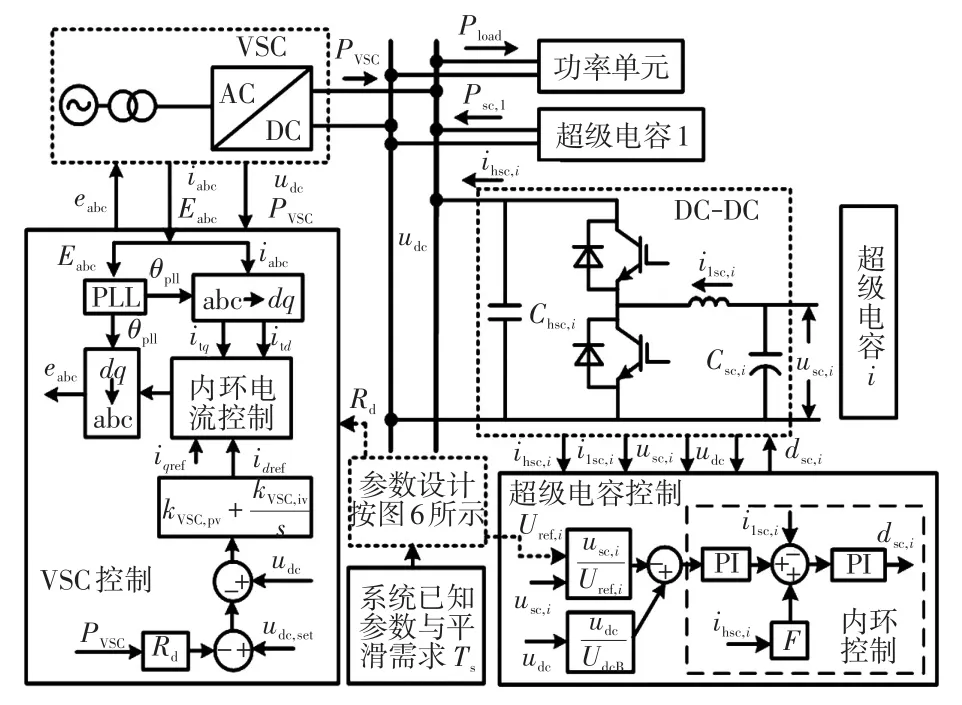
图2 系统结构与各单元控制Fig.2 System structure and control of units

图2中直流微电网功率和直流电压的基准值分别为PN和UdcB。VSC控制中udc,set为直流电压参考值，其中，Rd为下垂系数，kVSC,pv与kVSC,iv为电压环比例和积分系数，idref与iqref分别为dq轴参考电流，itd与itq为采样点dq轴电流分量，θpll为锁相角，Eabc与iabc为三相电压电流，eabc为三相调制电压信号，Lf与Cf为滤波电感与电容。在上述控制下，稳态下VSC注入直流微电网功率与直流电压之间的关系式为

如果系统内存在多个平衡单元，那么直流电压将由所有平衡单元共同控制，功率单元的功率也将自动地在平衡单元间进行分配。

2.2 超级电容功率平滑协调控制方法

2.2.1 超级电容控制方法

本文提出了如图2所示的超级电容控制方法。该方法通过就地测量直流母线电压，进而控制电容电压，其中电容电压的电压参考值为Uref,i。该方法本质是令超级电容电压与直流母线电压相等，达到超级电容近似等效“直接”接入直流母线的目的。

图2超级电容控制中：usc,i为第i个超级电容的电压；Csc,i为超级电容的电容量；ilsc,i与ihsc,i为第i个超级电容的电容侧电流与直流母线侧电流；dsc,i为占空比信号。为了提高超级电容电压和直流母线电压的一致性控制动态响应，还采用了电流前馈控制，F为前馈系数。在前馈控制下，暂态过程中，超级电容电压和直流母线电压可认为近似相等，即

对电容电压参考值Uref,i的选择，决定了超级电容的电压运行水平，同时也能灵活调整该超级电容对系统贡献的等效惯量大小，从而达到不同的Ts平滑时间效果，这将在4.2小节详细介绍。通过图2所示的控制方法，超级电容不仅能够提供给系统等效惯量，还能根据直流母线电压调整自身的电压，仅通过一次控制同时实现了惯量提升与电容电压控制的动态解耦问题，简化了控制结构与设计。

2.2.2 等效惯量与多超级电容间的协调控制

1）超级电容提供的等效惯量推导

假设功率单元功率发生了大小为ΔPload的扰动，在直流电压额定点线性化后，该扰动会引起直流电压的变化，即

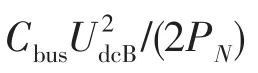
根据式（2）与电容的充放电动态关系可得超级电容的功率ΔPsc,i的动态关系式为

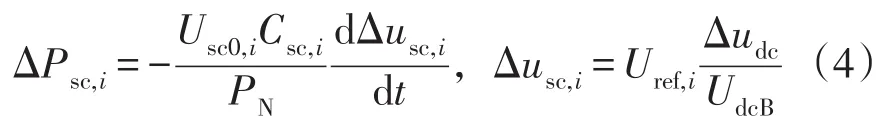
式中，Usc0,i表示该超级电容的稳态电压。再考虑直流电压额定点Usc0,i=Uref,i，根据式（3）、（4）及稳态电压关系，可推导ΔPsc,i与Δudc间的关系为

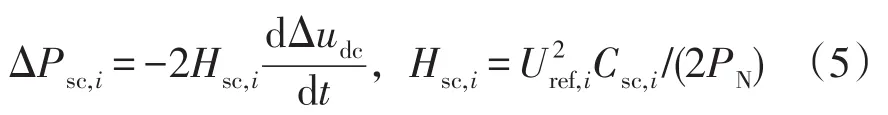
式中，Hsc,i为该超级电容贡献给直流微电网的等效惯量。通过调节该电容的Uref,i可调整超级电容的等效惯量，而该参数也决定了电容电压的运行水平。

2）多分布式超级电容间的协调控制

针对系统的平滑需求指标Ts，对多分布式超级电容贡献的整体等效惯量Hsc,all有一个大小要求，而如何实现协调配合便是如何解决该大小的Hsc,all总等效惯量在多分布式超级电容之间的合理分配。

根据式（5）单个超级电容的等效惯量表达式，当系统所需的惯量大小为Hsc,all时，可表示为多个超级电容的等效惯量相加，即

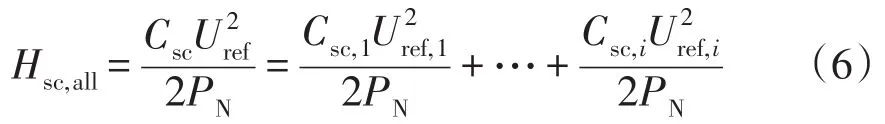
式中，Csc与Uref分别为多个分布式超级电容等效为一个集中式超级电容时的电容量与电压参考值。考虑每个超级电容系统此时的运行电压为Usco,i，该超级电容系统能够贡献的惯量有最大值Hsc,max,i，如式（7）所示。所以为使Hsc,all在多个超级电容间合理分配，可按照每个超级电容的最大惯量比进行分配，即

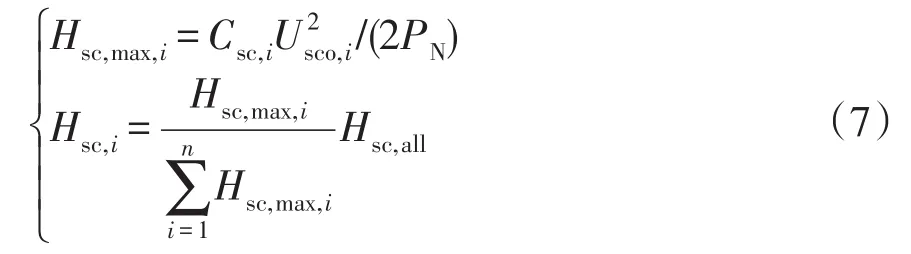
式中，n为超级电容数量。每个电容确定分配的等效惯量大小确定后，再根据式（5）的Hsc,i关系来确定该超级电容的Uref,i大小，即可实现超级电容间的等效惯量分配，其本质是根据不同超级电容的剩余容量进行分配，达到协调配合的目的。同时由式（5）也可看出，惯量的分配也即多超级电容暂态功率之间的分配为

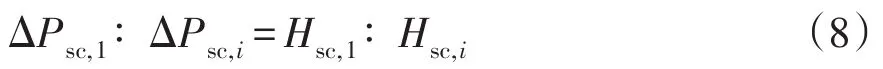
所以当Hsc,all确定后，则可按照上述原则在多分布式超级电容间进行合理分配。

3 基于等效惯量的暂态功率平滑分析

3.1 基于等效惯量的建模与参数分析

3.1.1 基于等效惯量的建模

首先建立系统的数学分析模型，直流母线电压、所有超级电容的暂态功率总和ΔPsc以及VSC的功率输出数学模型为

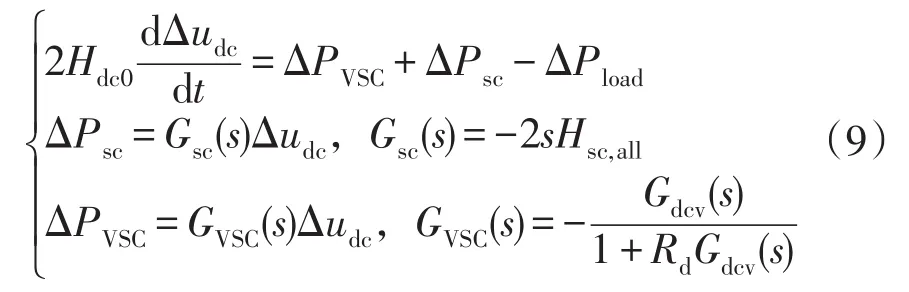
由于电流环响应较快，在式（9）对VSC的建模中可忽略电流环的影响，式中Gdcv(s)为电压环PI控制。

根据式（9）可推导出直流母线的传递函数为

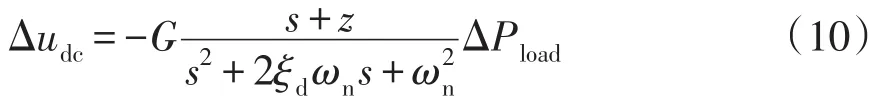
式中各参数可表示为

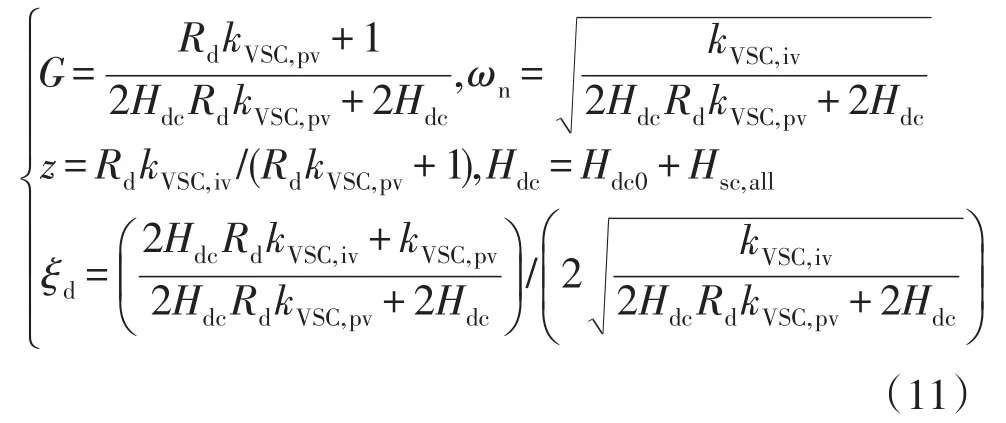
从式（10）可以看出，系统可简化成一个含一阶零点的二阶传递函数，根据该传递函数的动态性能指标要求，则可实现对超级电容电压的设计。

3.1.2 系统参数对平滑效果的影响

通过上一小节的各表达式可知，影响平滑效果的主要有控制参数Uref、VSC电压环PI控制参数、系统自身的功率等级PN以及下垂系数Rd。

1）Uref与VSC电压环参数的影响

当Csc确定时，Hsc,all的大小由Uref决定，图3（a）给出了Csc=33 F、Uref不同时直流电压的单位阶跃响应，图3（b）给出了在 Csc=33 F、Uref=90 V时kVSC,pv与kVSC,iv变化时的直流电压动态响应。

图3（a）表明Uref的增加能明显增加直流母线电压的平滑效果，增大了系统的惯量。在本文考虑中，要想达到理想的平滑效果，基本目标是保证超调量为0，即 ξd≥1，由式（11）可以求出临界Uref,s的表达式为

在上述超级电容参数以及系统参数下，可由式（12）计算出此时Uref,s=64 V，且从图3（a）中可以看出，在Uref≥64 V时无超调量，也验证了式（12）的正确性。

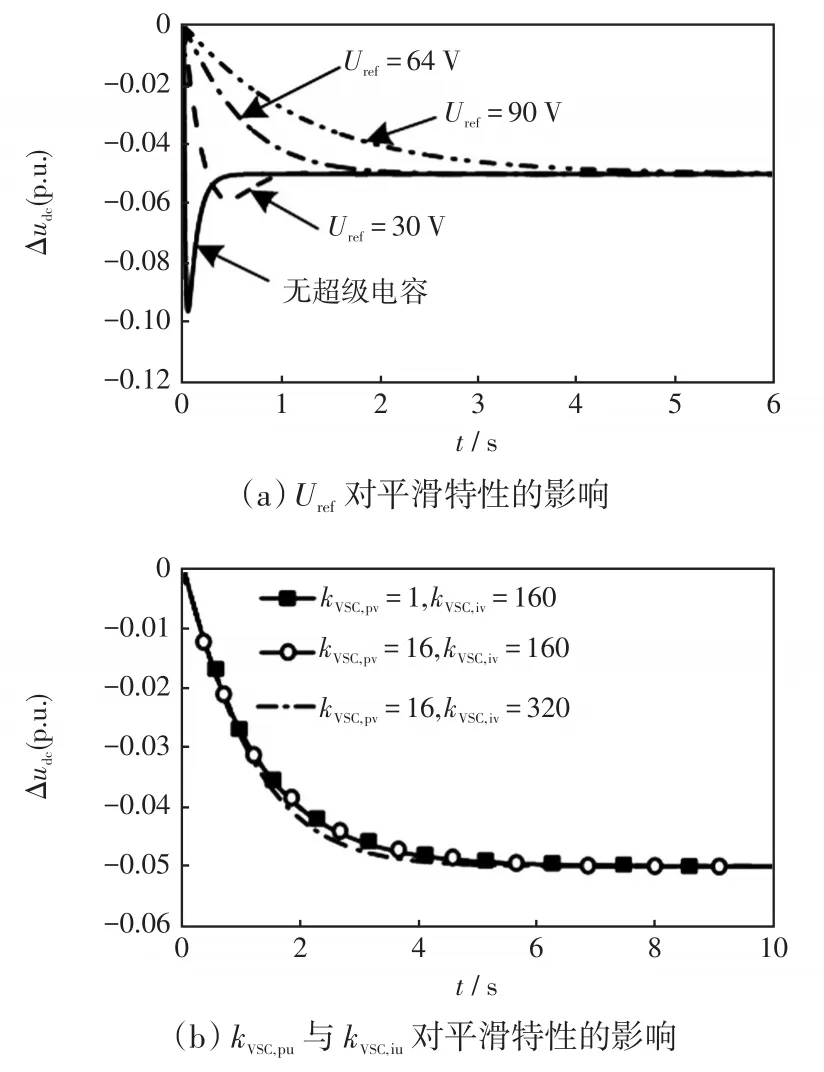
图3 Uref,s、kVSC,pv与kVSC,iv对功率平滑效果的影响Fig.3 Effects ofUref,s，kVSC,pvandkVSC,ivon power smoothing performance

同时，从图3（b）可看出功率平衡单元电压环PI控制参数的变化在理想的平滑效果下对直流电压动态影响很小，即超级电容对直流电压的平滑效果受功率平衡单元电压环PI控制参数的影响较小。

2）PN与Rd参数的影响

图4给出了在Csc=33 F、Uref=90 V下二者变化时的直流电压单位阶跃响应。图4（a）表明相同的等效惯量在PN越小的系统里平滑效果越好，当PN较大时会明显降低平滑效果；从图4（b）可以看出，Rd的增加会使相同的等效惯量下系统平滑效果更好。

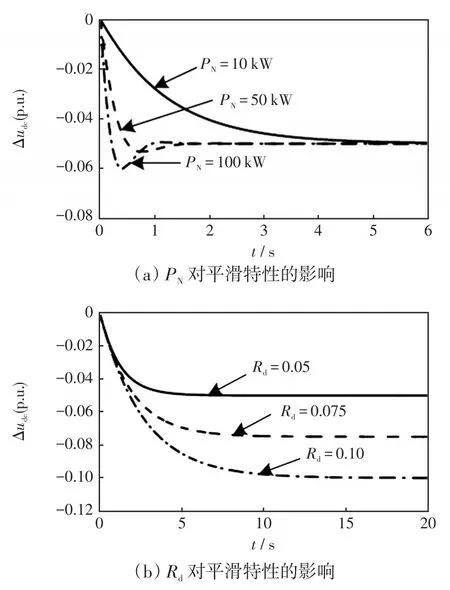
图4 PN和Rd参数对功率平滑特性的影响Fig.4 Effects ofPNandRdon power smoothing characteristics

3.2 模型降阶与关键控制参数设计

为简便地实现平滑效果的指标量化，本节将对系统进行模型降阶，定量刻画等效惯量、Rd系数与Ts三者之间的关系，进行关键控制参数设计。

3.2.1 模型降阶

利用模型（10）解析获得Ts关于等效惯量及Rd的表达式，但是形式较为繁琐。考虑到由于要想达到比较良好的平滑效果，基本目标是保证直流电压波形的超调量为0，应保证阻尼比ξd≥1。在该条件下，模型（10）将有两个负的实极点与一个零点，根据自动控制原理可知，当其中某一节点与零点距离较近时，该极点与该零点对系统动态性能的影响将近似抵消，系统动态性能由所剩极点主导。基于此，将推导模型（10）降阶模型，使等效惯量与Rd关于Ts的定量关系更加简洁。

在过阻尼下，可推导出（10）的两个实极点分别为

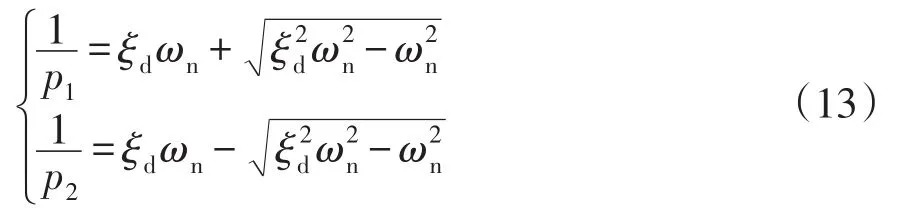
由 ξdωn与 ωn的表达式可知，当Hdc较大时为

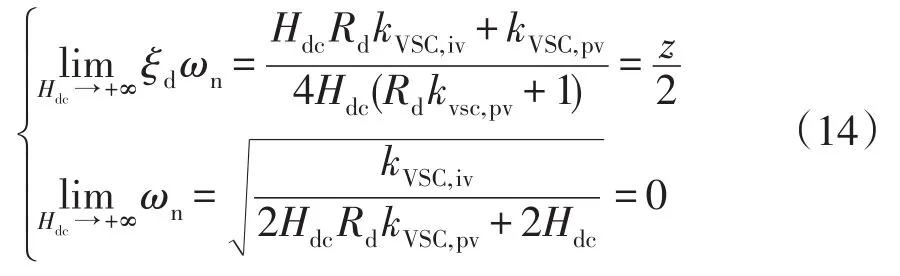
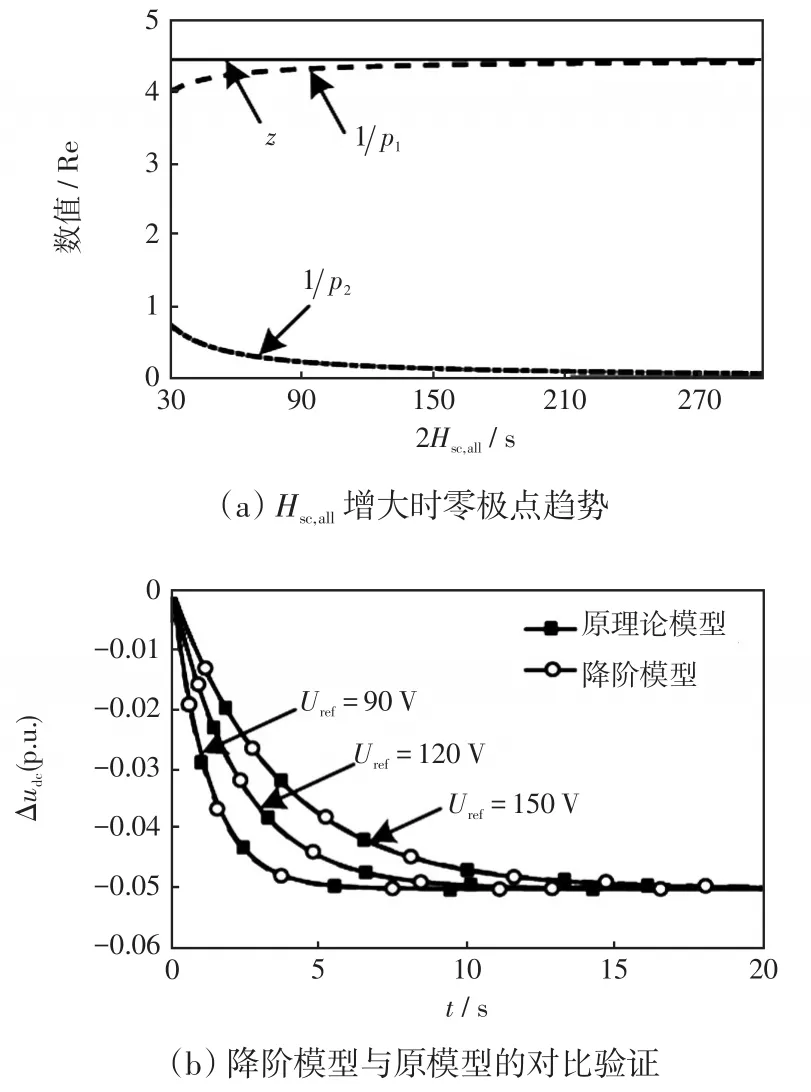
图5 Hsc,all变化时极点与零点的变化与降阶和等效模型对比Fig.5 Changes in poles and zeros whenHsc,allvaries，and the comparison between reduced-order and equivalent models

图5（b）对比了Csc=33 F时，不同Uref下降阶模型与原模型的结果，从图5（b）中可以看出二者基本重合，验证了降阶模型（15）的有效性。

如果系统要求保证平滑时间为Ts，由于一阶模型的调节时间（到达终值的95%）为3p2，那么即可根据该时间确定Hsc,all来保证3p2=Ts，从而实现对平滑效果的定量化设计。为更加简洁地表示p2，通过式（15）可以获得直流电压的时域解析表达式为

由稳态关系可知，Rd=zGp1p2，结合式（16）与式（5）与（9），可得所有超级电容功率和的时域解析式为

当发生功率扰动ΔPload时，系统内超级电容的功率应瞬间对该扰动进行支撑，即在t=0时刻，ΔPsc=ΔPload，所以可得

3.2.2 关键控制参数设计

从式（18）可以看出，Rd与Hsc,all的增加均会增加系统的平滑时间，即平滑效果。Rd一般会根据VSC的自身额定容量与系统允许的电压偏差ΔVpu进行设计，理论上而言，Rd能使系统运行最大的直流电压偏差不超过ΔVpu即可，但是从式（18）可知，在实现相同的平滑时间需求上，Rd的增加会降低对超级电容等效惯量的需求，故当PN为VSC额定功率时，系数Rd为

当Rd确定后，再按式（18）确定Hsc,all并按2.2.2小节中最大惯量比分配的原则分配给各超级电容，计算出各超级电容的电压参考值，如图6所示。

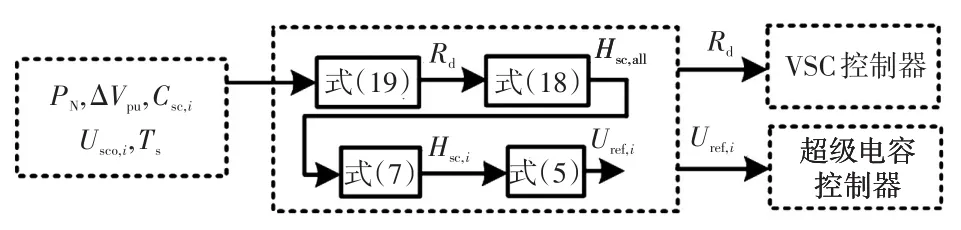
图6 关键控制参数设计Fig.6 Design of key control parameters

4 仿真验证

本文基于PSCAD/EMTDC软件搭建了图2所示的详细开关模型，对本文所提出的方法进行了仿真验证。功率单元通过DC-DC变流器与电阻负载进行模拟。两组超级电容系统（SC#1与SC#2），通过图2中所示的DC-DC接入直流母线，直流系统通过一台DC-AC接入交流电网模拟VSC运行。系统详细仿真参数如表1所示，系统功率基准PN=10 kW，允许的电压偏差ΔVpu=5%，故在以下仿真中根据图6计算可得Rd=0.05。

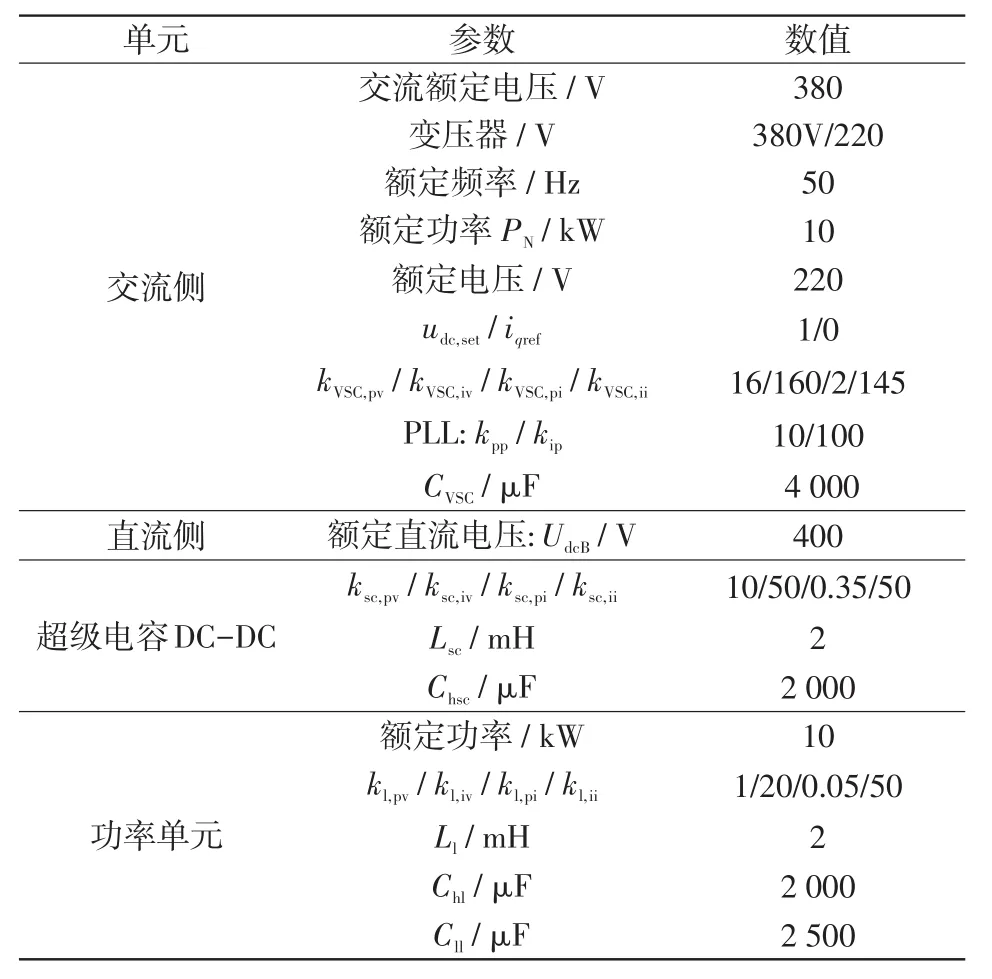
表1 系统基本参数Tab.1 Basic parameters of system

4.1 工况1仿真验证

假定平滑需求Ts=15 s。

工况1.1：两组电容物理参数相同。两个相同的分布式超级电容，参数均为Csc,i=33 F，二者电压均为Usco,i=200 V，则二者应该均分等效惯量，各自承担25 s等效惯量（Hsc,all=50 s），由图6可计算出，Uref,i=123.1 V，且二者暂态功率相等。

工况1.2：两组电容物理参数不同。SC#1参数为Csc,1=33 F，当前电压Usco,1=200 V；SC#2的参数为Csc,2=33 F，当前电压为Usco,2=141.42 V。SC#1最大惯量为SC#2的2倍，按照惯量分配，当Hsc,all=50 s时，根据图6可求两组超级电容的电压标幺参考值为Uref,1=142.13 V和Uref,2=100.5 V，暂态功率满足ΔPsc,1∶ΔPsc,2=2∶1。仿真结果如图7所示。

当t＜40 s时直流母线电压工作在1 p.u.，超级电容电压工作在各自的设定值Uref，工况1.1中SC#1与SC#2均为123.1 V，工况1.2中usc,1=142.13 V，usc,2=100.5 V，与理论值一致。

在t=40 s时，系统投入0.6 p.u.（6 kW）负荷，扰动瞬间超级电容快速放电补偿功率缺额，从图7（d）可以看出工况1.1中两组等效惯量相同的超级电容的暂态功率相等，均为0.3 p.u.，而工况1.2中由于SC#1的等效惯量为SC#2的2倍，故SC#1的暂态功率为SC#2的2倍，分别为0.4 p.u.与0.2 p.u.。由于两个工况中对直流系统贡献的总等效惯量相同，所以可以从图7（a）、（b）看出，两个工况中的VSC功率与直流母线电压动态一致，图7（b）表明该动态过程的调节时间接近15 s，也证明了理论分析的正确性。

图7 Ts=15 s时的仿真结果Fig.7 Simulation results whenTs=15 s

t=80 s时，系统切掉0.6 p.u.负荷，同样在扰动瞬间超级电容快速充电，暂态功率仍按最大惯量比进行分配，扰动结束后udc=1，超级电容电压恢复到初始值。

4.2 工况2仿真验证

为了验证即使超级电容系统运行数量不同仍然能够达到相同的平滑效果，与工况1.1进行对比，工况2中电容参数与工况1.1一致，但是仅运行SC#1，此时根据图6可计算出工况2中SC#1的Uref,1=174.1 V。

工况2的仿真结果如图8所示。在t=40 s与t=80 s处系统内功率单元分别投入0.6 p.u.与切掉0.6 p.u.负荷，从图8（d）可以看出，相比工况1.1中的两组电容平分扰动功率，工况2中的SC#1独自承担该扰动功率，工况2中的SC#1的电容电压从174.1 V放电至168.9 V后又充电至174.1 V，均与理论值一致。在两个功率扰动下，从图8（a）、（b）可以看出，工况1.1与工况2下VSC功率与直流母线动态几乎一致，证明了理论分析的正确性。

图8 工况2的仿真结果Fig.8 Simulation results in Case 2

从工况1及工况2的仿真结果可以看出，尽管超级电容的配置不同，但通过控制参数设计均可满足系统的平滑需求，且只要超级电容贡献的总等效惯量相同，对直流系统的平滑效果一致，表明了本文控制方法、理论分析与设计的正确性。

5 结论

本文针对含多分布式超级电容的直流微电网提出了一种功率平滑协调控制方法。通过理论分析与仿真验证可得出以下结论：

（1）该方法仅依靠就地测量的信息便能够使超级电容在系统发生功率扰动时快速充放电，平抑扰动功率，且通过设计能够按照系统需求平滑直流母线电压与功率平衡单元的功率输出；

（2）在功率平滑的同时，该方法还通过一次控制就地且简便地实现了超级电容电压的控制，简化了控制结构；

（3）通过设计获得能够满足系统平滑需求的等效惯量后，依据超级电容间最大惯量比分配的原则能够实现多分布式超级电容的等效惯量合理分配，实现多电容间的协调配合。