一种应用于光伏电站的无源箝位移相全桥变换器

李 明

（青海民族大学计算机学院，西宁 810007）

光伏并网逆变器是将太阳电池所输出的直流电转换成符合电网要求的交流电的核心设备。光伏并网逆变器的性能影响和决定整个光伏并网系统是否能够稳定、安全、可靠、高效地运行，同时也是影响整个系统使用寿命的主要原因。DC/DC高频隔离型光伏并网逆变器具有电气隔离、质量轻、体积小等优点，单机容量在几kW以内，系统效率大约在93%左右[1]。

DC/DC变换器是高频隔离型光伏并网逆变器的核心部件，对设备的运行起到至关重要的作用。随着对电源变换模块体积和效率的要求不断提高，移相全桥DC/DC变换器开关频率越来越高[2]。

传统移相全桥变换器缺点是二次侧会出现占空比丢失，因为一次侧电流换相的过程中可能会不足以给负载供电，造成二次侧整流桥的所有二极管导通，负载处于续流状态，其两端电压为零，这样就会导致二次侧丢失了部分电压方波，占空比减小[3-4]。此外，变换器的开关管电压应力箝位在高输出电压应用场合，需要选取高电压等级、导通电阻较大的MOSFET，从而增加了变换器电路成本和开关管的导通损耗，降低了变换器的效率。文献[5]提出了一种新型大功率等级的DC-DC变换器拓扑方案，提高光伏系统总效率，但未实现高升压比，无法应用于中高压直流电网的接入[6-8]。文献[9]采用Boost变换器，当输入和输出电压相差很大时，占空比接近于1，升压电感电流纹波很大，开关管关断电流也很大，因此开关管的开关损耗较大，使变换效率较低。文献[10-11]分别提出了一种含有有源软开关辅助电路的直流升压变换器，其变换器的工作效率由于软开关的应用得到了相应的提升，但在该类变换器中由于开关管数量的增加，导致控制方式变得更为复杂，在变换器工作于高频状态时，电路的电磁干扰特性较差。

本文设计了一种二次侧带无源箝位移相全桥电路。可实现全软开关，其中超前臂通过开关的并联电容和二次侧的大滤波电感实现零电压开通，滞后臂通过一次侧变压器漏感和二次侧的箝位电容实现零电流关断。该电路不仅具有高频电气隔离的特点，减少了占空比丢失，同时前后级控制相互独立，控制简单，后级电路器件承受的电压应力低，控制方式不需要更多变动，电压输出稳定，纹波系数小，适用于高频、大功率、高功率密度场合[12]。

1 研究对象的拓扑结构与工作原理

1.1 拓扑结构

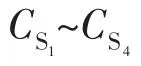
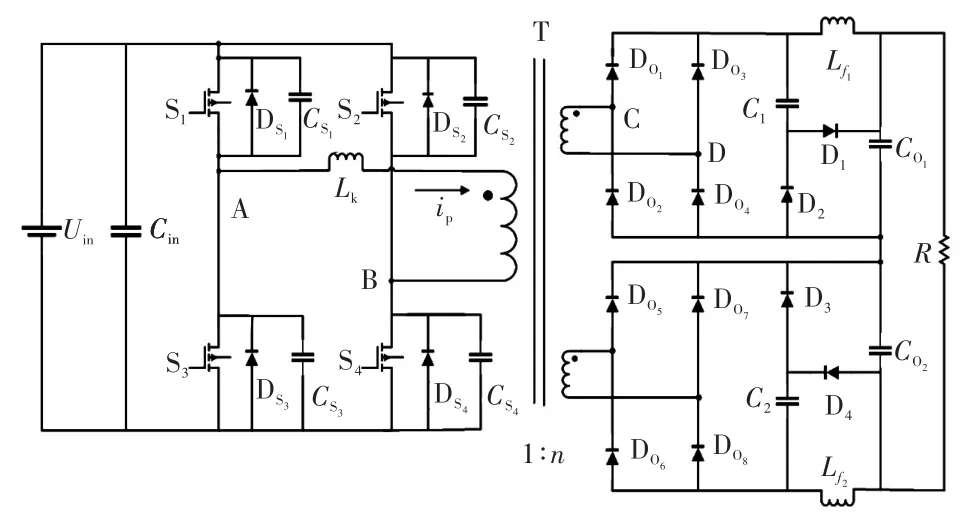
图1 无源箝位移相全桥电路Fig.1 Passive clamp phase-shift full-bridge circuit

1.2 工作原理

变流器的工作时序图如图2所示，开关管S1～S4分别为4个开关所对应的状态，S1、S4触发脉冲一致，S2、S3触发脉冲相同，二者相差180°。uAB为一次侧的电压波形，uCD为二次侧的电压波形，ip为一次侧电流波形。同时要对拓扑进行验证，需要满足以下条件：

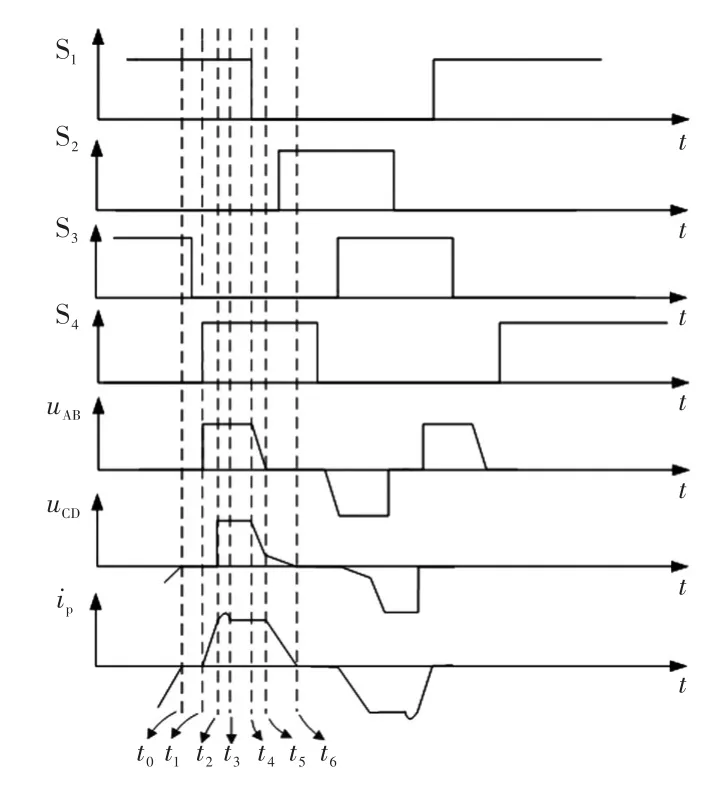
图2 变流器控制时序Fig.2 Control sequence of the converter

（1）电路中所用到的二极管、开关、电感、电容、电阻均为理想元件；

（2）二次侧的两个串联电路的所有参数严格一致，包括变压器参数；整流全桥电路所有二极管；无源箝位电路的二极管、电容；滤波电路的电容、电感；

（3）输出滤波电感够大，可以看作电流源；输出滤波电容足够大，可以看作电压源。

由于在一个工作周期内开关信号、电压、电流波形是对称的，接下来以t0为起始时刻，对该变换器的半个工作周期内各个阶段进行讲述，分析其工作原理。

（1）工作状态1(t0～t1)如图3所示。在该阶段起始时刻，S1和S3处于导通状态，但是此时一次侧电流下降为0，为S4实现零电流关断做好准备，此时一次侧与二次侧电压也为0，两个箝位电容C1、C2在上一个周期结束放电，整流全桥的8个二极管进行续流，全部导通。

（2）工作状态2(t1～t2)如图4所示。在该阶段起始时刻，S4导通。原先一次侧的电流为0，但由于存在电压漏感，使得一次侧电流不能突变，故S4实现了零电流导通。此时S1与S4同时导通，一次侧电流开始上升，由于此时一次侧电流刚开始上升，不能支撑负载电流，二次侧的整流二极管仍旧处于续流状态，全部导通，因此二次侧电压uCD为0。

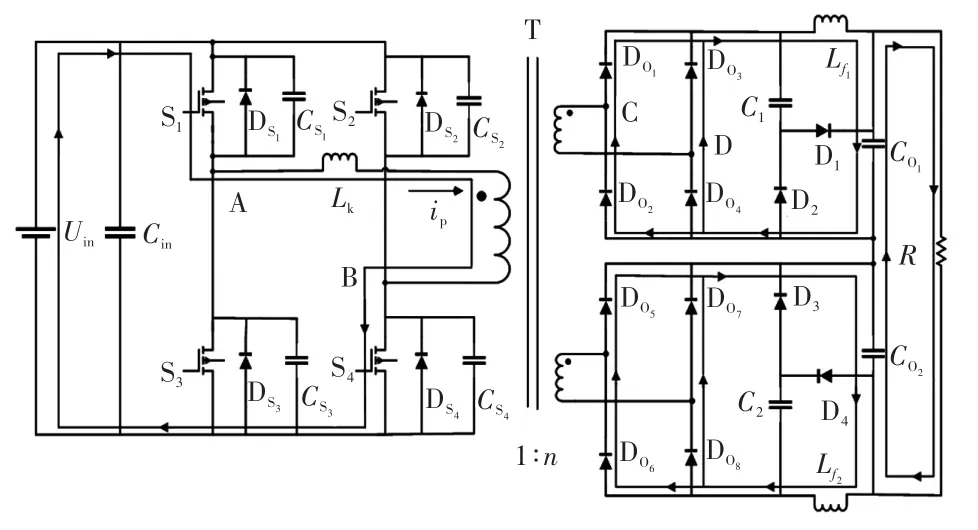
图4 工作状态2Fig.4 Working state 2

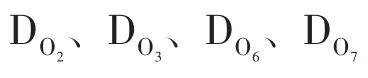
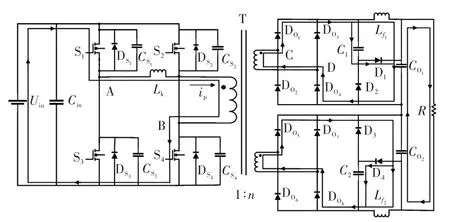
图5 工作状态3Fig.5 Working state 3

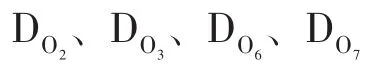
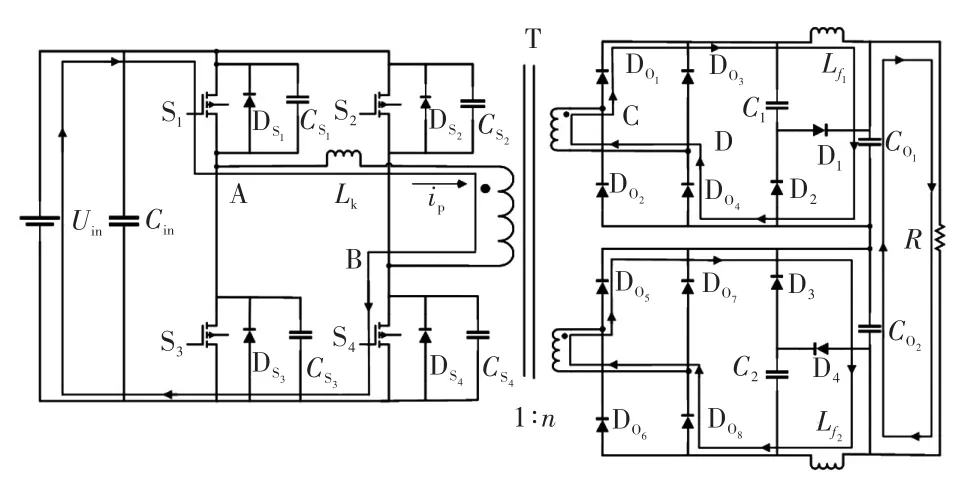
图6 工作状态4Fig.6 Working state 4

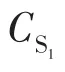
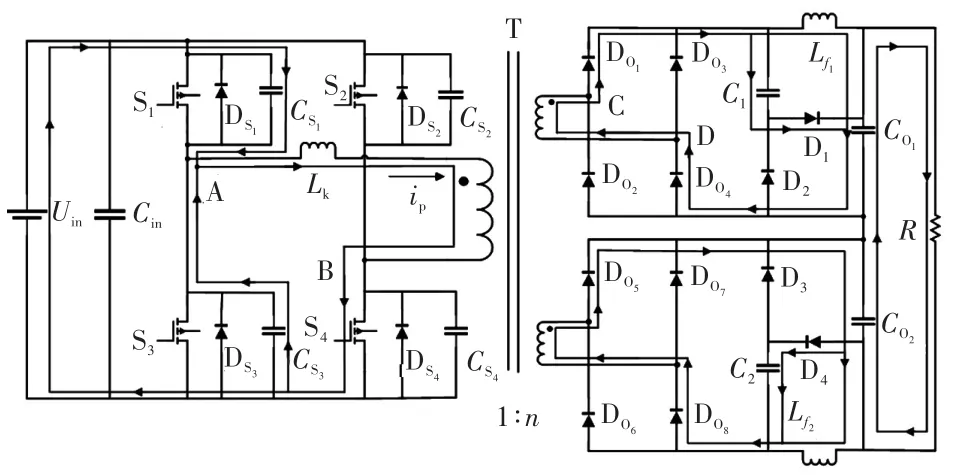
图7 工作状态5Fig.7 Working state 5

图8 工作状态6Fig.8 Working state 6

变换器下半周期的工作状态与上半周期类似，但是波形相反。

2 控制策略

2.1 软开关实现

为了提高电路的效率，需要在电路中采用软开关实现开关的零电压ZVS（zero voltage switch）和零电流ZCS（zero current switch）通断[13]。电路通过超前臂开关并联的电容充放电与二次侧的大滤波电容实现软开关，滞后臂开关则通过一次侧的变压器漏感与二次侧的箝位电容充放电实现软开关。

（1）超前臂零电压开关。

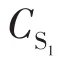
式中：Ip为一次侧电流有效值；UCD为二歇侧电压有效值。

（2）滞后臂零电流开关。

由对称工况可知，在工作状态1之前的一个状态，箝位电容C1与C2开始放电，并在工作状态1期间放电完毕，从而一次侧电流下降为0。在工作周期2时刻，由于一次侧漏感Lk的存在，S2可以零电流导通。因此钳位电容所储存的能量必须大于一次侧漏感所储存的能量。对于MOS管来说，存在着一个开通时间ton，需要远小于工作状态2的时间(t2-t1)。根据这两条约束，可以得出滞后臂实现零ZCS的条件为

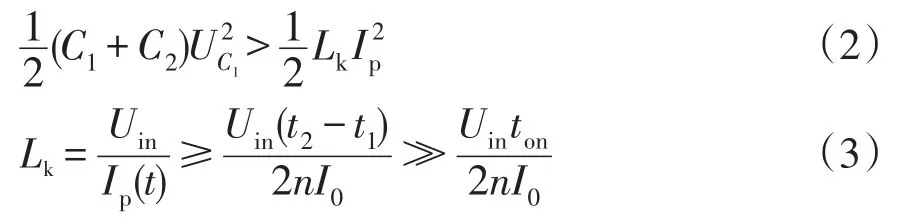
2.2 电压应力分析

二次侧加入辅助箝位电路后，整流二极管两端的电压被限制，电压尖峰得到抑制，与传统硬开关变换器相比，无需再添加缓冲电路。但二次侧加入电容后会增加整流二极管的电压应力，这对器件会有一定影响。图9是该拓扑与其他添加次级辅助电路的结构对比。

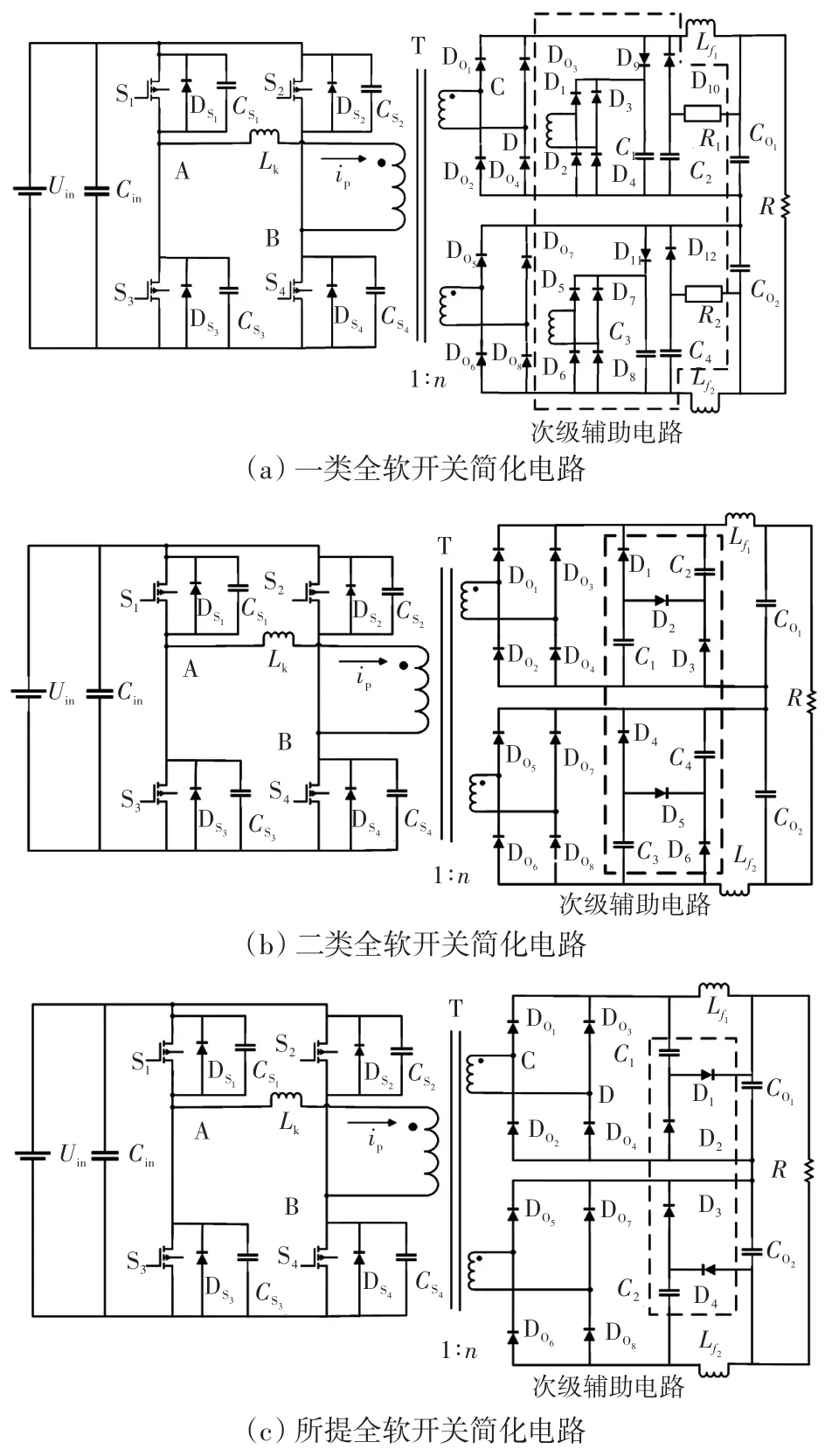
图9 几种次级辅助电路拓扑对比Fig.9 Comparison among several secondary auxiliary circuit topologies

箝位电容的选取直接影响到整流二极管尖峰抑制的效果和滞后桥臂的零电流开关。

由此可得箝位电容两端在t2时刻达到的最大电压为

整流二极管的电压在t2也达到最大值，即

由式（6）可得整流二极管电压与占空比的关系曲线，如图10（a）所示，上述几种拓扑对应的二极管最大应力如图10（b）所示。

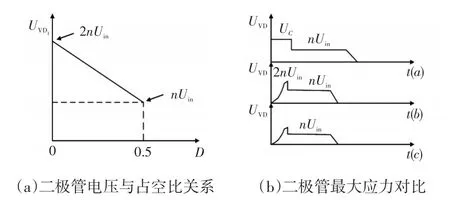
图10 整流二极管电压与占空比关系以及二极管最大应力对比Fig.10 Relationship between rectifier diode voltage and duty cycle，and comparison of maximum stress in diode

由图10可知二极管承受电压与开通占空比呈比例关系，占空比越大，电压应力越小；反之，占空比越小，电压应力越大。正常情况下为达到技术要求，一般设计整流二极管的电压应力为nUin的1.2倍。图9（b）相对于（a）的所用的辅助器件少了很多，但由于两个电容串联和漏感的作用使得谐振电压很大，最大可达到UO的两倍，图9（c）的结构简单，不需要额外的辅助二极管，减少损耗，同时整流桥电压的应力峰值可以根据开关器件相移角和谐振电路的参数的调整而调整。

相对于传统移相全桥电路来说，a、b、c三种方法都在二次侧增加了带电感、电容的次级辅助电路，成本增加，但减小和避免了换相失败的风险和器件损耗，解决了占空比丢失的问题。通过表1可以看出，所提的方法使用的器件个数少，效果明显。

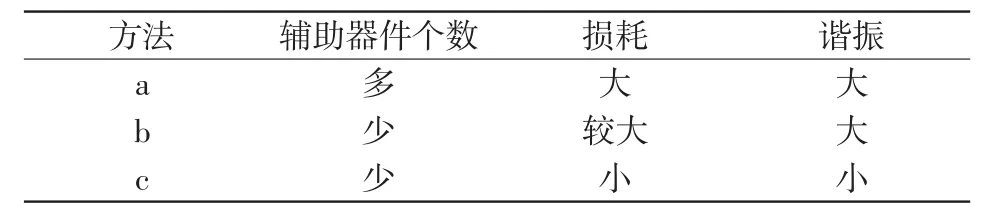
表1 不同结构拓扑的比较Tab.1 Comparison among different topologies

2.3 最大功率点跟踪控制

本文设计的DC-DC变换器的控制策略如图11所示。采用双闭环结构[14-16]，将光伏板输入电压Upv电流ipv经过MPPT模块后得到的电压与输出的电压Uo进行对比，将偏差经过PI控制器调节，采取电压外环电流内环的方法，得到的脉动进行脉冲宽度调制，从而实现整个升压的控制。

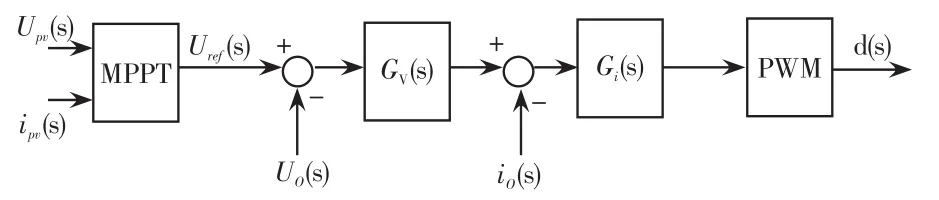
图11 DC/DC控制电路Fig.11 DC/DC control circuit

其中最大功率追踪MPPT选用改进的电导增量法。电导增量法的原理如下。

光伏阵列的功率及导数可表示为

定义电导和电导增量为

最大功率时有dP/dU=0，整理有：

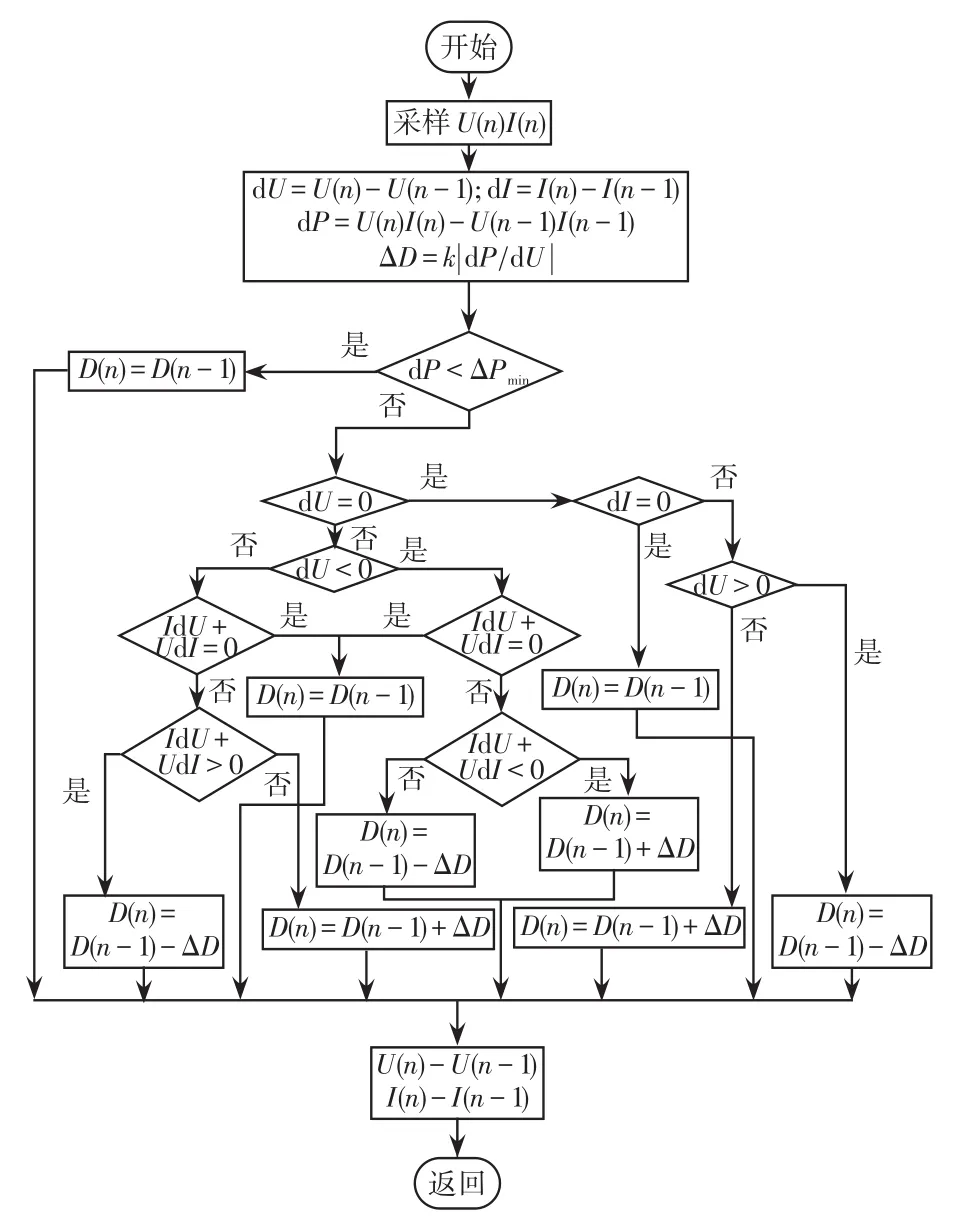
图12 改进的电导增量法流程Fig.12 Flow chart of improved conductance increment method

通过上述流程图进行判断得到下一次步长的取值，进而得出下一次迭代的电流和电压值。

3 仿真验证

移相全桥主电路的参数如表2所示。

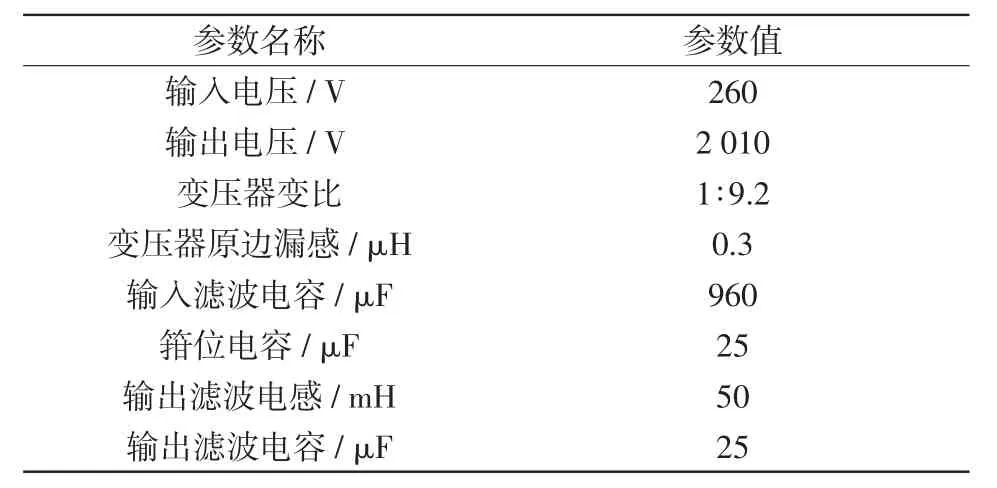
表2 移相全桥主电路的参数Tab.2 Parameters of phase-shift full-bridge main circuit

设置开关的导通时间如图13所示，可见，3个开关管同时导通的时间占整个周期比例较小，故占空比损耗可以忽略不计。

图13 一次侧开关管的调制信号Fig.13 Modulation signal of primary-side switch tube

3.1 整流二极管电压应力分析

如图14（a）示，开通时刻整流桥的最大电压应力为nUin的160%。改变箝位电容C1容量，由50 μF减至25 μF，整流桥的最大应力减小，降至145%，如图14（b）所示。降低开通占空比D至60%，电压应力明显下降，降至nUin的130%，如图14（c）所示。当调整变压器漏感Lk降至0.3 μH时，可以看到整流桥最大应力几乎为nUin，如图14（d）所示。故对于本文的模型，通过适当调整开关器件相移角和谐振电路的参数可以调整器件的最大电压应力。

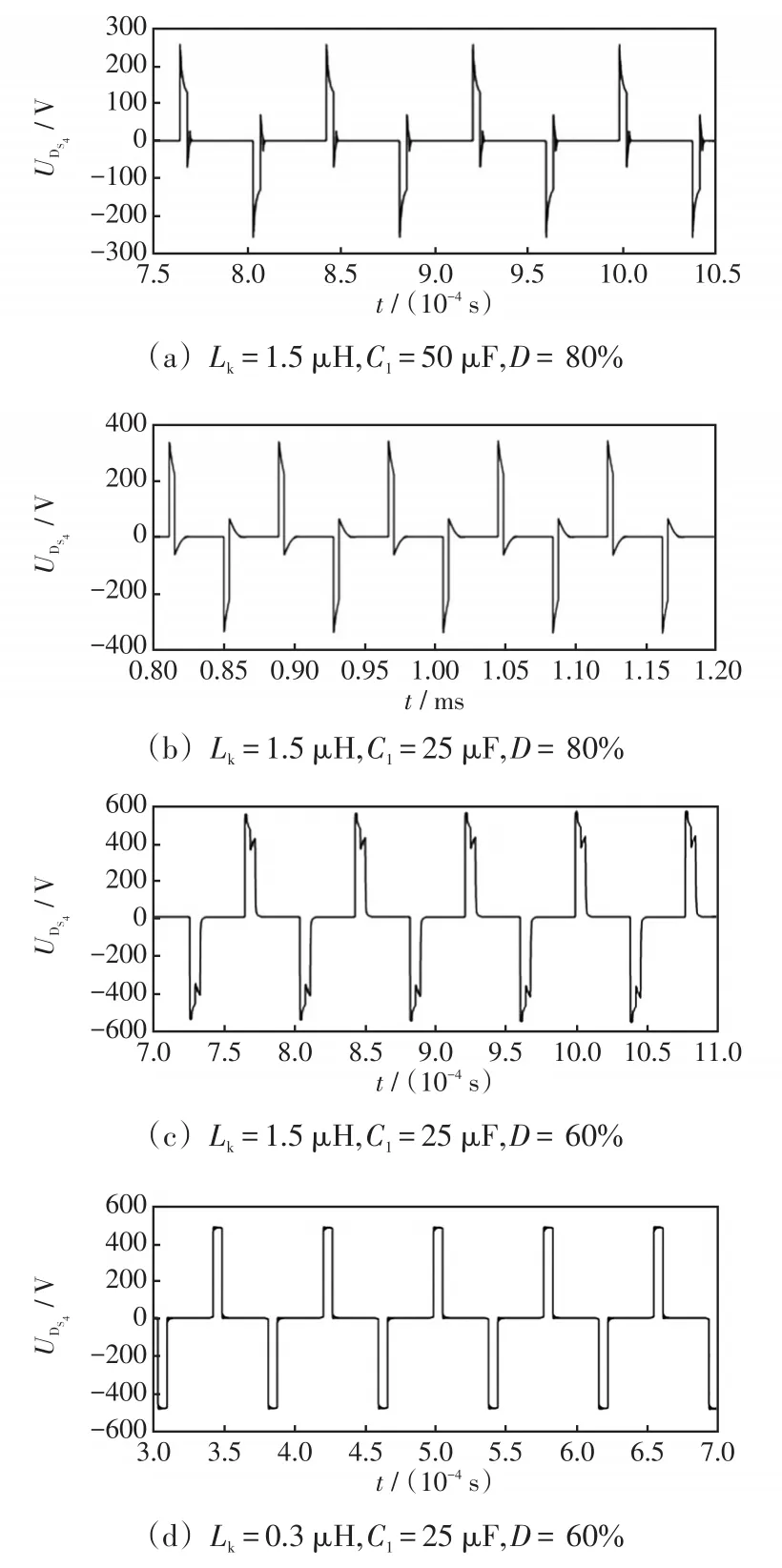
图14 不同参数对电压应力的影响Fig.14 Effects of different parameters on voltage stress

3.2 最大功率跟踪及抗扰动分析

变光强情况下，电流、功率、电压的仿真波形如图15所示。在仿真中，光强输入侧是一个阶跃信号，在30 ms和70 ms分别改变光强输入的阶跃信号，将其看成扰动信号，可以看到，在30 ms后光强从1 000 W/m2降到600 W/m2，电压电流随之降低，在50 ms时通过功率追踪后趋于稳定。光强越小，光伏板的电流-电压特性曲线就越往下移，最大功率点电压也越小，电流与功率也越小。70 ms后升高信号，电压电流值立刻回升，功率点在73 ms达到最大稳定，响应速度快。同时也可以看出在电压达到一定值之前，电流保持不变，到达一定值之后，电流急速下降，这与光电池电流-电压特性一致[17]。然后在电压到达最大之后基于MPPT算法电压开始减小并产生波动，仿真所得图形与理论分析一致。

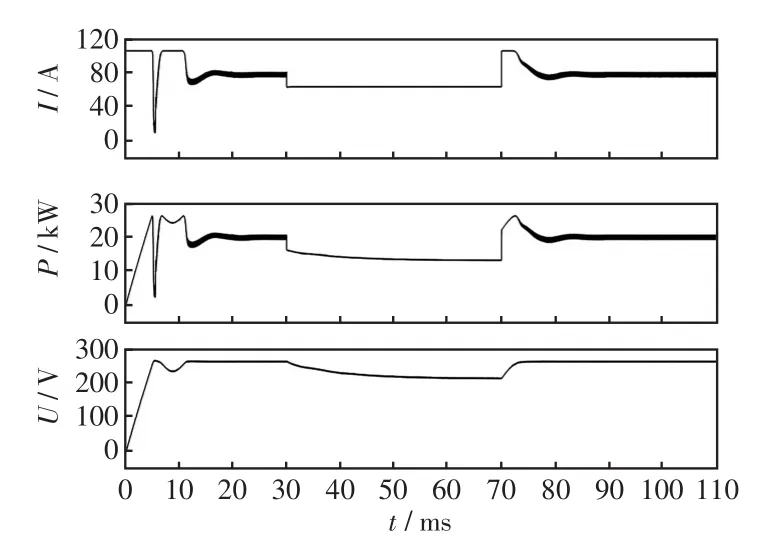
图15 变光强情况下MPPT算法效果Fig.15 Effect of MPPT algorithm under variable light intensities

变温情况下，电流、功率、电压的仿真波形如图16所示。在仿真中，温度输入侧是一个阶跃信号，在30 ms从25℃升高到60℃，在70 ms回到了25℃。可以看到在波形图中30 ms时，电压从260 V降低到了235 V，电流与功率均有所降低，在3 ms后趋于稳定。70 ms时升高温度，将其看成扰动，电流与电压也立刻回升[18]，功率点在2 ms后到达最大且稳定。根据之前的分析，温度越大，光伏板的电流-电压特性曲线就越往下移，最大功率点电压也越小，电流与功率也越低，仿真图形与理论分析一致。

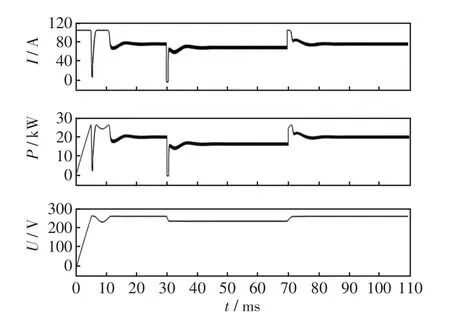
图16 变温情况下MPPT算法效果Fig.16 Effect of MPPT algorithm under variable temperatures

根据两个波形图可以看出该算法对于最大功率点的跟踪速度较快，而且跟踪效果稳定。在外界出现扰动的时候，光伏的电压波动在合理的范围之内，是一种可靠的算法。

3.3 软开关的验证

在软开关过程中，电流与电压处存在一个死区，由于流过开关的电流是从开关开通的时刻开始上升，因此可以用开关信号代替开关的电流状态。由于开关信号最大为1，因此在进行比较时需要将导通信号放大一定倍数。在进行验证时，采取开关两端的电压Ug与导通信号Dg进行比较。在进行验证时，采取开关两端的电压Ug与导通信号Dg进行比较。

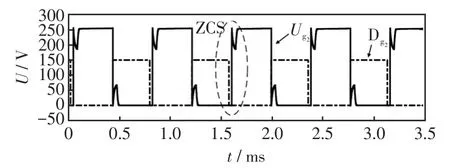
图17 滞后臂软开关仿真Fig.17 Simulation of lagging-leg soft switching

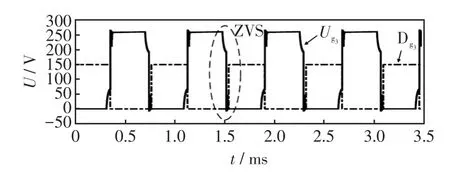
图18 超前臂软开关仿真Fig.18 Simulation of leading-leg soft switching

3.4 升压验证

输入、输出电压与电流波形如图19所示，由图19分析可以得出，电压电流在很短时间的波动后进入稳定运行状态，均无超调。电压实现了从260 V升压到2 000 V，响应速度快。稳定后输出电压纹波系数为0.12%，输出电流纹波系数为0.10%，与传统全桥升压变换器相比，电压增益增高，稳定性得到了很大提升。

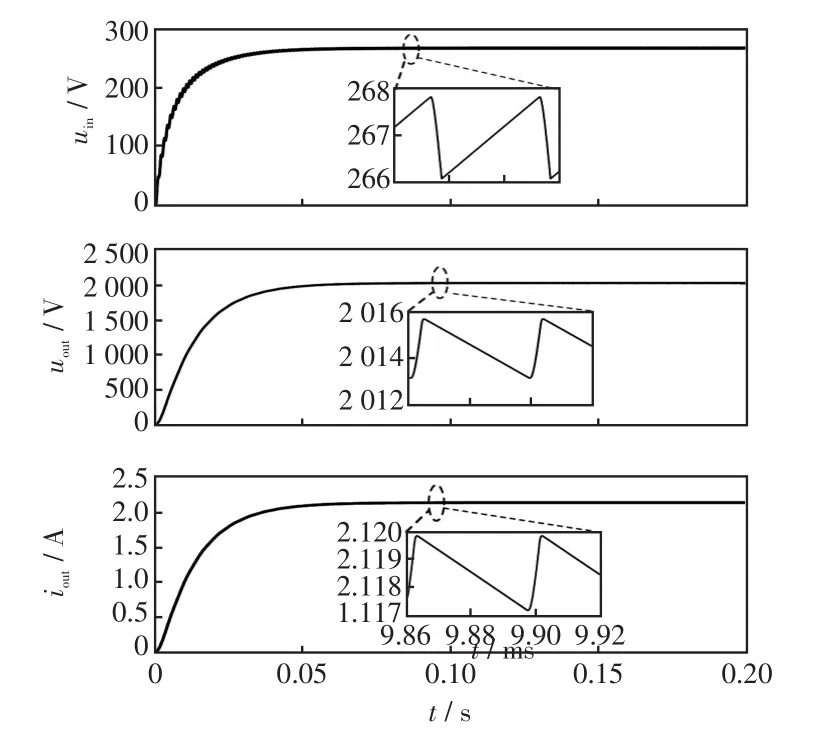
图19 输入、输出电压与电流波形Fig.19 Waveforms of input/output voltage and current

4 结语

本文设计了一种新型的无源箝位移相全桥变换器，整流电路选取移相全桥电路，二次侧添加由一个电容两个二极管组成无源箝位辅助电路。可实现全软开关，该电路不仅具有高频电气隔离的特点，升压效果良好，改善了占空比丢失，而且响应速度快，无超调且纹波系数小。同时前后级控制相互独立，控制简单，后级电路器件承受的电压应力低，控制方式不需要更多变动，电压输出稳定，纹波系数小，适用于高频、大功率、高功率密度场合。基于光伏电源设计了控制策略，实现了最大功率追踪，具有良好的抗扰动性。并通过仿真进行理论验证，为大型光伏电站远距离传输能量提供新的理论支撑。