基于快照反馈的短期电力负荷组合预测方法

孙颢一，易灵芝，2，刘文翰，邱东洲，赵 健

（1.湘潭大学自动化与电子信息学院湖南省多能源协同控制技术工程研究中心，湘潭 411105；2.湖南省风电装备与能源变换2011协同创新中心，湘潭 411105；3.辽宁华电铁岭发电有限公司，铁岭 112000）

短期电力负荷预测是电力负荷预测的重要组成部分之一，主要指预测未来几个小时、一天至几天的电力负荷，是指定日前发电计划的基础，对电网的经济运行有着重大的意义[1-3]。随着我国经济水平的日益提高以及电力系统改革的不断深入，对短期负荷预测的精度要求也越来越高。因此，有必要研究短期负荷预测的新技术及方法，以满足工程技术的要求、提高负荷预测的可靠性与精度。

经过长时间的发展，短期电力负荷预测已较为成熟。目前，电力负荷预测方法主要分为3类。第一类是基于传统数学统计模型的预测方法，如时间序列法[4]、多元线性回归法[5]、指数平滑法[6]等。传统数学统计模型的方法模型简单、计算简捷，预测速度较快；但其模型鲁棒性较差，且对于随机性和复杂性强的负荷预测能力较差。第二类是基于机器学习的预测方法，如神经网络法[7-9]、支持向量机[10-11]等。基于机器学习的预测方法在非线性系统预测中被广泛使用并取得了较好的预测精度；但机器学习模型预测的结果很大程度上取决于数据的数量及质量，大数量且高质量的数据往往更容易取得更为准确的预测结果。但电力负荷实际工程应用中，负荷数据的噪声干扰及数据空缺会导致机器学习模型难以从数据中建立能够实际有效准确预测的模型。第三类是组合预测方法：①通过分配权重结合多种算法[12-13]，常见的权重分配方法有算术平均法、方差导数法、均方差导数法、Shapley值法等；②将负荷进行分解预测，例如小波变换[14]、经验模态分解EMD（empirical mode decomposition）[15]、变分模态分解技术VMD（variational mode decomposition）等。由于传统数学统计模型方法和机器学习方法有各自的局限性，因此组合预测方法应运而生。文献[16]首先通过EEMD将电力负荷数据分解为由高到低的不同本征模态函数IMF（intrinsic mode function），随后分别使用多元线性回归方法和GRU神经网络方法对低频部分和高频部分进行快速准确的预测，最后将所得各预测结果组合后得到完整的预测结果。文献[17]采用VMD技术将原始历史负荷序列分解为多个特征互异的模态函数，对每个模态函数进行特征分析并分别通过采用改进粒子群算法优化过网络权值的DBN网络进行负荷预测，提高了短期负荷预测的精度。

本文提出了一种基于快照反馈机制的VMD算法 VMDSF（variational mode decomposition with a snapshot of feedback）和一种带有循环滑窗策略的长短时记忆网络CSLSTM（long short-term memory with circular sliding window），并组合成为一种新的短期电力负荷组合预测方法。首先使用VMDSF将原始电力负荷序列分解成多个子序列；然后结合网格搜索法对CSLSTM进行最优参数寻找，得到含有最优模型参数的电力负荷短期预测模型；最后，使用2013年澳大利亚4个区域的电力负荷数据集，对本文方法进行算例测试，测试结果表明了本组合模型的有效性。

1 基于VMDSF-CSLSTM的短期负荷预测方法

1.1 基于快照反馈机制的改进VMD算法

VMD分解算法被广泛应用在电力负荷预测领域，但VMD算法需要预先确定模态数K，模态数K的值由预测模型在训练集上的表现程度决定，其值与算法预先设定的中心频率差值Δf有关，它的大小很大程度上影响预测模型的精度；VMD算法还存在不能通过所有IMF相加得到原序列的问题。

针对上述问题，本文提出了VMDSF。快照反馈VMD算法具有无需预先设置模态数K值的优点，本文提出的VMDSF算法主要步骤如下。

步骤1 中心频率差值Δf=2fn，初始化模式数量Kn=2，xkn(t)=x(t)。

步骤3 将得到的模式分量和原始信号与所有模式分量相减得到的残差信号输入至预测模型，在模型运算至5%时生成模型快照，保存模型权重，并且在测试集上运行预测模型，计算预测结果10次的RMSE均值。

步骤4 当跳出迭代条件满足时，停止快照反馈和分解，模式数量等于Kn。否则进行步骤5。

步骤5令Kn+=1，重复“步骤2”～“步骤4”过程。

其中，K值寻找为凹函数问题，结束循环的判别条件为：①本代快照模型RMSE均值大于上一代RMSE模型均值；②总步数大于20。

根据上述算法不仅能够解决VMD分解后原始信号不能还原的问题，而且可以确定模态数K。

1.2 基于循环滑窗策略的LSTM预测模型

本文使用LSTM模型作为短期电力负荷预测任务的基础模型，在短期电力负荷预测任务中需要预测24、48乃至更多的负荷点，当预测负荷点较多或时间步长较长时，LSTM模型就会存在较大的累积误差，因此会导致模型的预测误差变大。

针对上述问题，本文提出CSLSTM，设置时间步长Step=1（本节所提的时间步长不是LSTM模型中的参数，而是预测循环进行的位置），预测长度为Length，每次训练长度为t结束后模型只针对第t+1时刻负荷进行预测，然后将预测值回添至训练集末端；接下来将训练集往后滑动一个窗口，Step=Step+1，继续循环迭代预测，直至预测长度满足Step＞Length。

因此本文提出的基于循环滑窗策略的LSTM的预测模型步骤如下。

步骤1 设置预测长度Length，初始化时间步Step=1，保存预测结果列表为pre=[]。

步骤2 设置LSTM模型超参数，将长度为t的训练集进行模型迭代训练，并根据LSTM内部设计通过最小化RMSE损失函数，使用随机梯度下降法寻找模型最优权重参数，若迭代次数满足预设超参数迭代次数，则得到LSTM预测模型。

步骤3 将验证集数据传入“步骤2”中得到的LSTM预测模型，对第t+1时刻负荷进行预测，Step=Step+1，将预测值添加至pre列表，将预测值回添至训练集末端。

步骤4 当Step＞Length成立时，停止循环和滑窗操作，预测结果为pre列表。否则将训练集滑动一个窗口，保证训练集长度仍然为t，然后重复“步骤2”～“步骤4”过程。

上述预测模型能够保证每次预测的精确度，并且累积误差较小。

1.3 VMDSF-CSLSTM短期负荷预测模型

本文提出一种基于快照反馈短期电力负荷组合预测方法VMDSF-CSLSTM。该模型使用VMDSF算法将负荷信号分解为多个IMF，将负荷信号减去所有IMF得到残差序列，如图1所示。

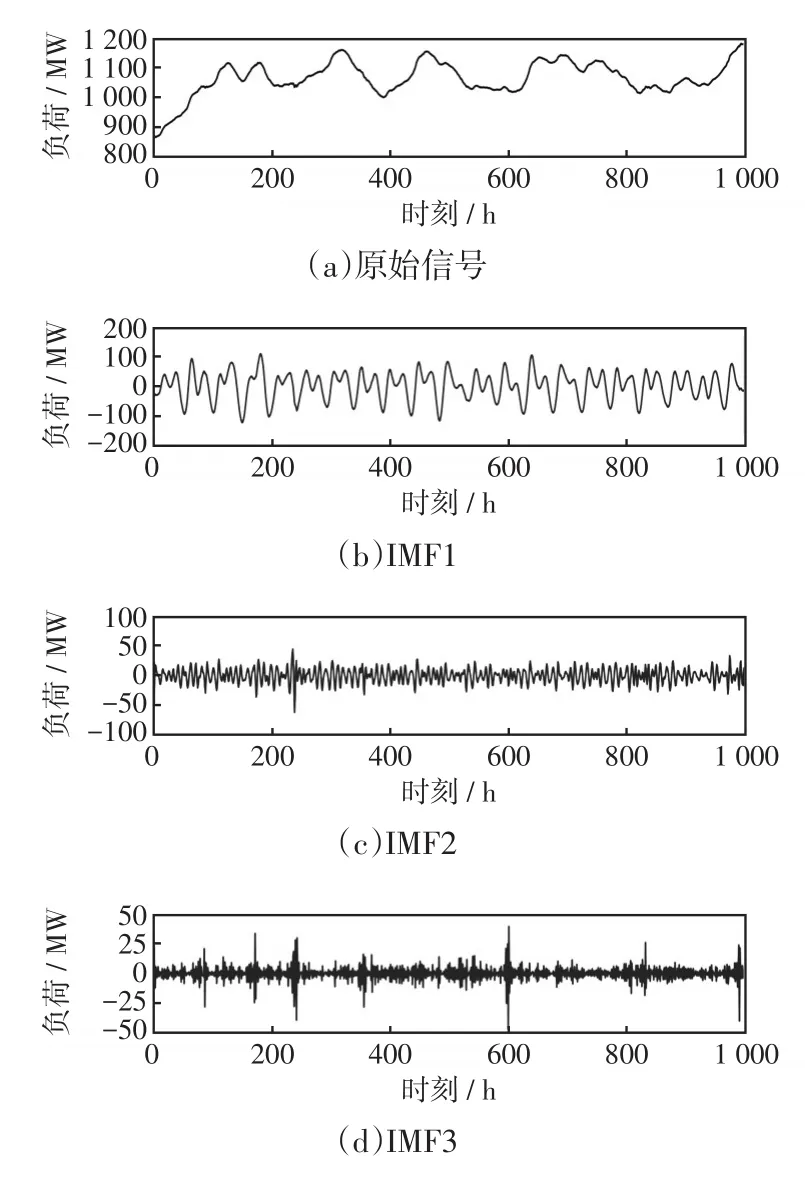
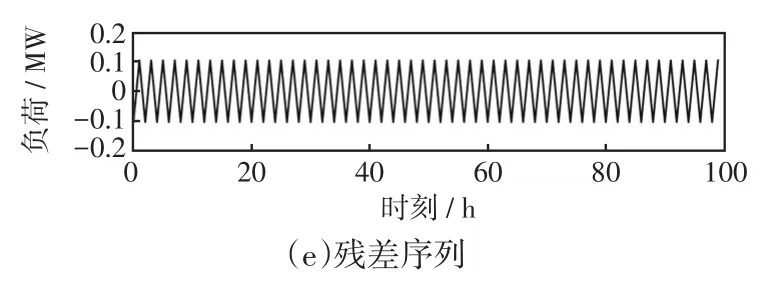
图1 当K为3时VMD分解信号示例Fig.1 Example of VMD decomposition signal when K=3

基于VMDSF-CSLSTM模型的短期电力负荷预测流程图如图2所示，算法步骤如下。

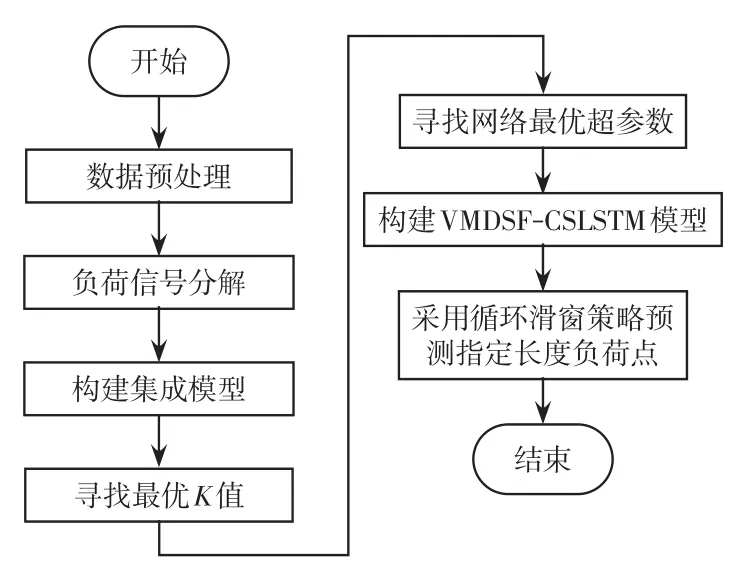
图2 基于VMDSF-CSLSTM模型的短期电力负荷预测步骤Fig.2 Steps of short-term power load forecasting based on the VMDSF-CSLSTM model

步骤1 数据预处理。对缺失值进行前后均值补全，划分训练集、测试集、验证集。

步骤2 负荷信号分解。对训练集进行初次VMD分解，将得到的IMF与原负荷信号减去所有IMF生成的残差序列，将所有子序列进行0-1归一化处理。

步骤3 构建集成模型。将步骤2得到的IMF与残差序列构建对应LSTM子模型，使用先验知识设置子模型超参数，连接各子模型的输出索引得到集成模型。

步骤4 寻找最优K值。使用训练集训练该模型，然后采用快照反馈机制预测指定长度的负荷点，当循环至指定长度的5%时生成模型快照，反馈至模型前端，当满足快照反馈策略的跳出条件时，得到最优K值。

步骤5 寻找网络最优超参数。设定最优K值，然后设置需寻优的超参数及范围，采用网格搜索法寻找网络最优超参数。

步骤6 使用最优K值和网络最优超参数构建VMDSF-CSLSTM模型，采用循环滑窗策略预测指定长度的负荷点，完成电力负荷短期预测。

本文使用4个公开数据集验证VMDSF-CSLSTM模型的有效性和泛化能力。

2 实验与结果分析

本文中归一化方式统一采用为0-1归一化消除数据量纲带来的影响，公式为

本文中模型评价指标统一为平均绝对百分误差MAPE（mean absolute percentage error）和均方根误差RMSE（root-mean-square error），

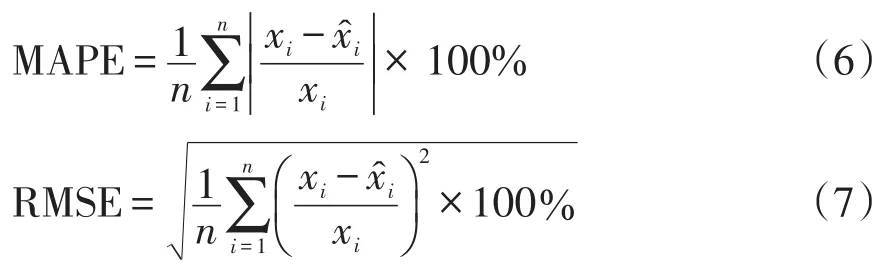
本文实验代码统一采用Python3.6编写，Tensorflow版本为1.7，实验平台为MacBook Pro（15-inch，2019），处理器 2.6 GHz Intel Core i7、内存 16 GB 2400 MHz DDR4，编辑器采用Pycharm专业版。

2.1 实验逻辑说明

本节实验分为三部分，实验逻辑如下。

（1）第一部分：首先使用先验知识配置CSLSTM模型超参数，然后分别使用预测值回填模式与预测值不回填模式进行预测，并在4个公开数据集上进行效果对比。

值得注意的是，实际工程中应用的模式是基于预测值回填模式。因为在负荷预测的实际应用中，当模型预测第二个负荷点时，并不知道第一个负荷点的实际值，所以需使用第一个负荷点的预测值，但这种模式对于模型的挑战很大。本文提出的VMDSFCSLSTM正是使用预测值回填的实际预测方案，从侧面印证了该模型的实际预测能力和优越性。

（2）第二部分：由于基本的机器学习模型在使用预测值回填方案进行预测时，从第二个负荷点开始累积误差成倍增大，模型几乎呈完全不拟合的状态，无法比较模型的优劣势。所以，本部分实验均采用预测值不回填的方案，比较CSLSTM与LSTM、BPNN及SVR的效果。

（3）第三部分：使用实际回填模式的VMDSFCSLSTM使用网格搜索寻找最优网络超参数，然后分别与基于VMD-CSLSTM、EMD-CSLSTM的预测模型进行对比。

2.2 实验数据说明及分析

本节实验使用的数据为2013年澳大利亚4个区域能源市场的电力负荷需求数据，分别为塔斯马尼亚州（TAS）、昆士兰州（QLD）、新南威尔士州（NSW）和南澳大利亚州（SA），4个数据集均为周期为48时刻的数据；采用前1 000个时刻的数据作为训练集，1 000～1 048时刻的数据作为测试集。部分数据如图3所示。

图3 4种公开数据集部分数据Fig.3 Part data of four open data sets

图4为展示各数据集负荷的滞后相关性，结果表明，在各数据集中，t时刻的负荷与t+1时刻、t+2时刻及t+3时刻的负荷均有很强的相关性，所以本节采用前3时刻负荷数据预测第4时刻负荷数据，并且数据集的相关性越高，预测结果相应越准。

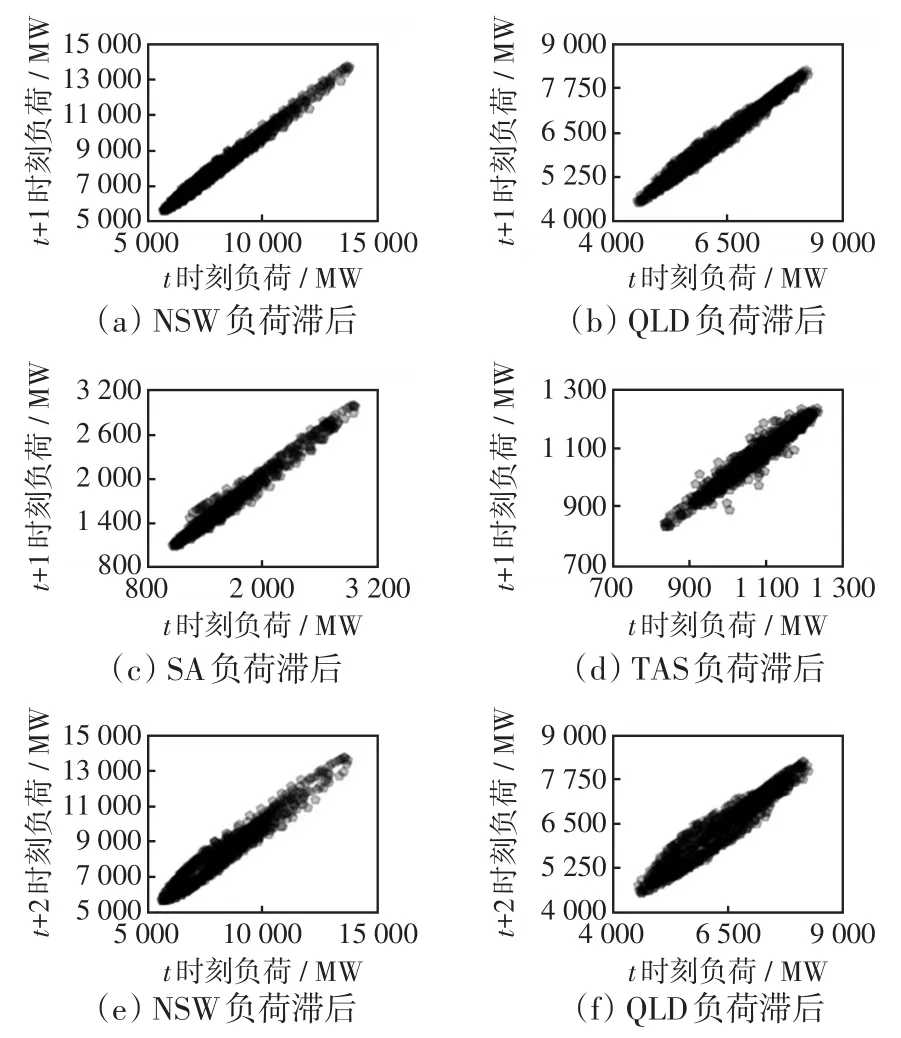
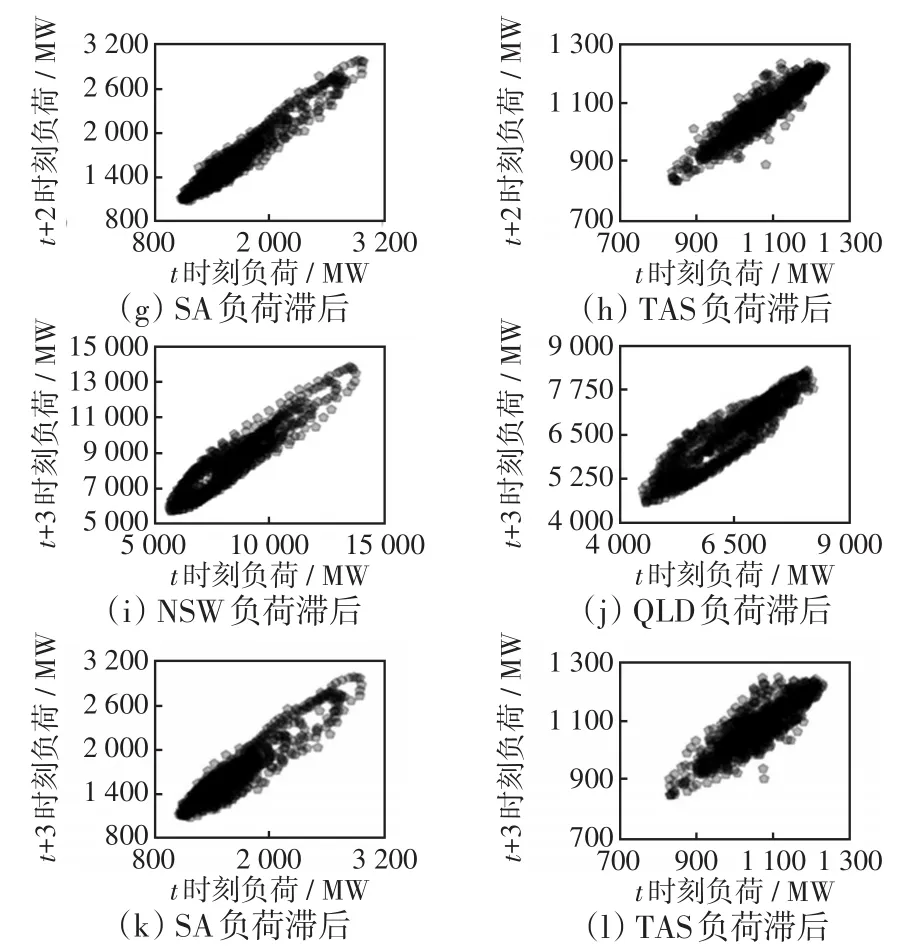
图4 4个数据集的滞后相关性Fig.4 Lag correlation of four data sets

图5为4个数据集各自的自相关性图，可以看出4个子图的值均不能快速收敛至零值附近振荡，4个数据集均为非平稳时间序列。

图5 4个数据集的自相关性Fig.5 Auto-correlation of four data sets

2.3 实验结果分析

2.3.1 第一部分实验

本节第一部分实验，选用先验知识配置具有良好模型效果的CSLSTM参数，模型超参数见表1。

表1 CSLSTM模型训练超参数Tab.1 Training super parameters of the CSLSTM model

图6中，CSLSTM表示带循环滑窗策略但不回填预测值的理想预测方案，CSLSTM-TRUE表示带循环滑窗策略且回填预测值的实际预测方案。各图分别为不同数据集1月部分CSLSTM、CSLSTMTRUE的预测曲线。可以看出，CSLSTM-TRUE在第一时刻预测时有较好精度，但随着模型误差逐渐加大，直至拟合能力完全丧失。此部分映证了在实际工程应用的情况下（即回填预测值的模式下），模型短期预测的难度和对于模型的挑战都非常大；从图中可看出CSLSTM拟合效果很好，但不是工程应用中的预测模式，只能对比算法本身效果，并不能应用于工程应用。

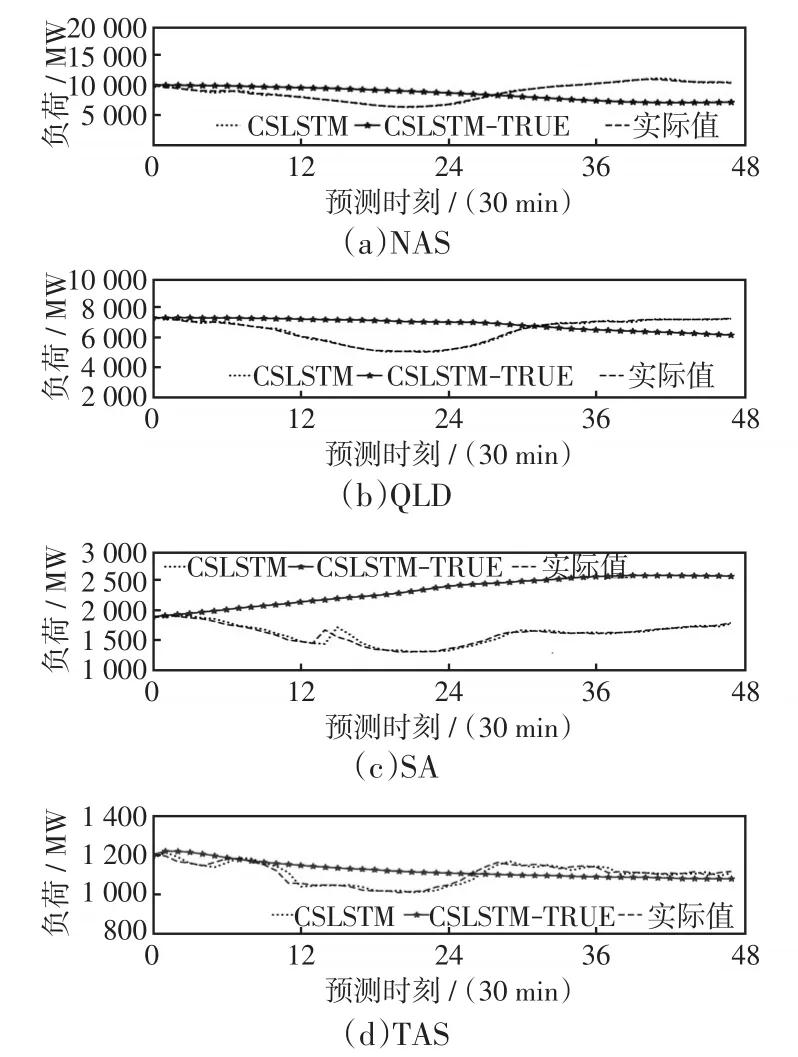
图6 两种预测方案效果对比Fig.6 Comparison of effect between two prediction schemes

2.3.2 第二部分实验

第二部分，将CSLSTM与LSTM、BPNN及SVR进行对比，采用各数据集典型的4个月份作为实验测试，训练数据采用每个月份前1 000样本点，测试数据采用每个月份第1 001～1 049个样本点。实验都采用理想化（不回填预测值）的预测方式，BPNN和SVR的超参数经最优调试，LSTM与CSLSTM采用相同的超参数，旨在证明带循环滑窗策略的CSLSTM模型的优势。

通过表2、表3可直观地看出CSLSTM多个数据集中均表现出较好的性能，得出以下结论：本文提出的CSLSTM方法与BPNN、SVR及LSTM相比具有更好的模型精度。

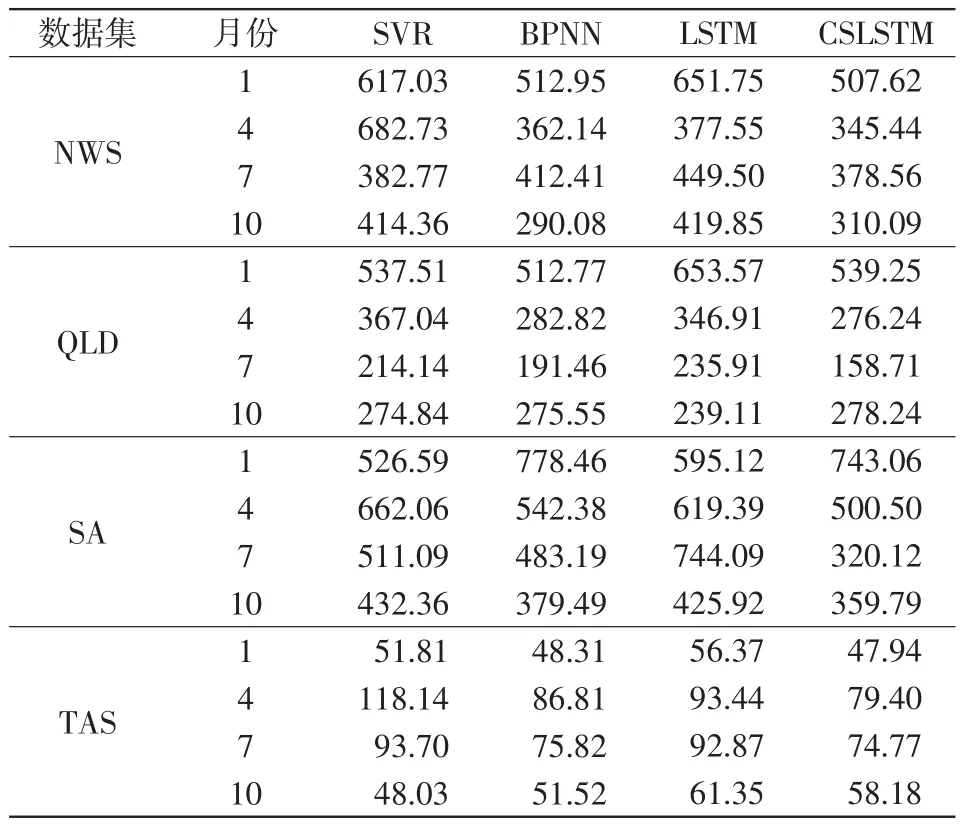
表2 4种算法在各数据集上RMSE的对比Tab.2 Comparison of RMSE of each data set among four algorithms

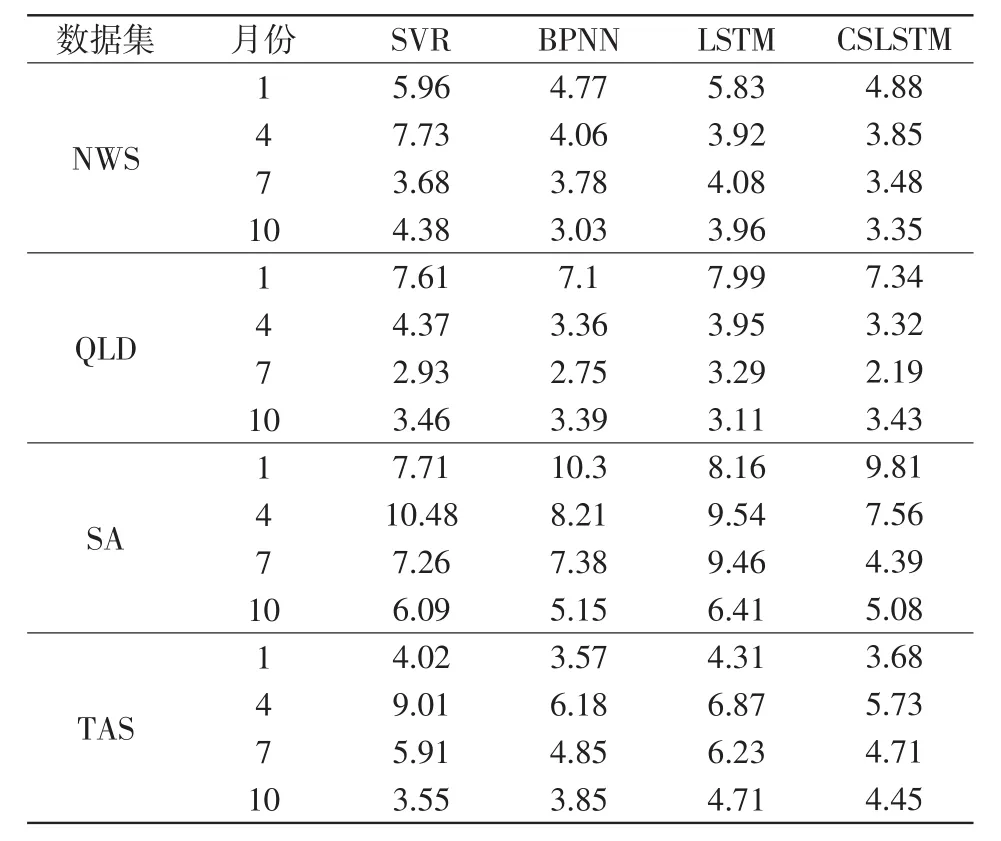
表3 4种算法在各数据集上MAPE的对比Tab.3 Comparison of MAPE of each data set among four algorithms

2.3.3 第三部分实验

第三部分采用各数据集典型的4个月份作为实验测试，训练数据采用每个月份前1 000样本点，测试数据采用每个月份第1 001～1 049个样本点。实验都采用实际工程应用的情况（回填预测值）。首先采用网格搜索法GS（grid search）对VMDSFCSLSTM寻找最优参数；然后将该模型与VMD-CSLSTM、EMD-CSLSTM进行对比。因为组合模型预测效果、泛化能力较好，所以该部分模型均使用将预测值回填的实际工程应用中的预测方式。

GS法遍历给定参数组合通过SA数据集1月份数据作为优化目标，来优化VMDSF-CSLSTM模型参数组合。选取模型的迭代次数、隐藏层神经元数、批次大小、优化策略、权重初始化方式作为优化参数。寻优参数及范围见表4。

表4 设置VMDSF-CSLSTM寻优范围Tab.4 Setting of optimization range of the VMDSF-CSLSTM model

通过GS寻找得到最优模型参数，模型参数如表5所示，再通过控制变量法画箱型图分析验证最优参数的有效性。

表5 VMDSF-CSLSTM最优模型超参数Tab.5 Super parameters of VMDSF-CSLSTM optimal model

图7为迭代次数对VMDSF-CSLSTM的预测性能影响对比箱型图，图中每个箱的含义为VMDSFCSLSTM在SA数据集7月份10次短期预测的RMSE与MAPE误差，横坐标为不同迭代数量。由图可知当迭代次数为600时，模型稳定性最优，模型预测MAPE值稳定在1以下。

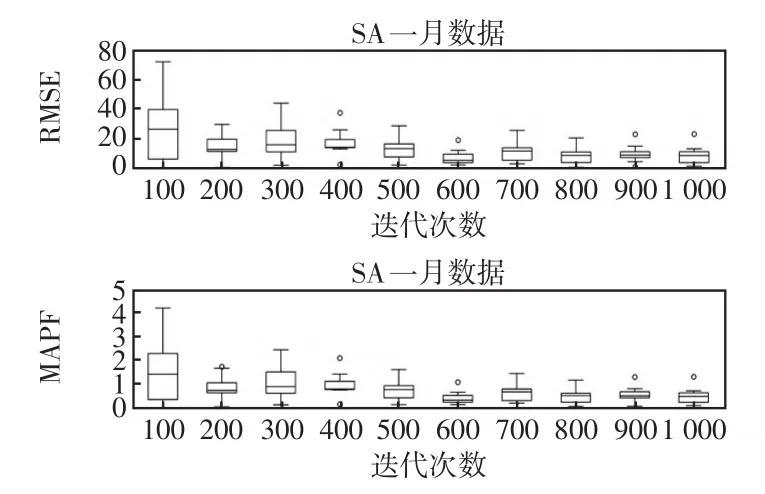
图7 控制变量法查看迭代次数对模型的影响Fig.7 Determinationoftheinfluencesofiterationnumbers on the model using the control variate method

图8是训练批次对VMDSF-CSLSTM的预测性能影响对比箱型图，图中每个箱的含义为VMDSFCSLSTM在SA数据集7月份10次短期预测的RMSE与MAPE误差，横坐标为不同训练批次。当训练批次设置为100时，模型有稳定的MAPE值域，且有较快的训练速度。

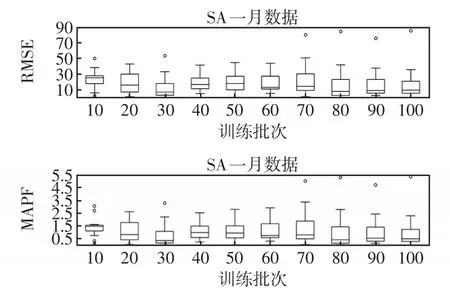
图8 控制变量法查看训练批次大小对模型的影响Fig.8 Determination of the influences of training batch size on the model using the control variate method

图9是隐藏层神经元数对VMDSF-CSLSTM的预测性能影响对比箱型图，图中每个箱的含义为VMDSF-CSLSTM在TAS数据集7月份10次短期预测的RMSE与MAPE误差，横坐标为不同的隐藏层神经元数。当隐藏层神经元数设置为10时，虽有一个离群值点但模型效果整体稳定。

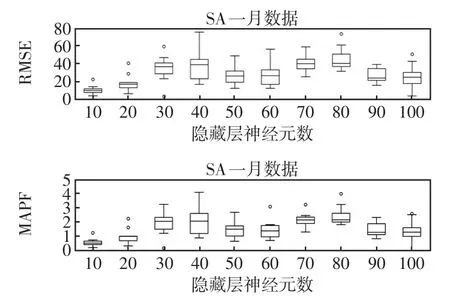
图9 控制变量法查看隐藏层神经元数对模型的影响Fig.9 Determination of the influences of hidden neuron numbers on the model using the control variate method

将使用最优参数配置的VMDSF-CSLSTM与VMD-CSLSTM、EMD-CSLSTM进行对比，实验中VMDCSLSTM集成模型的VMD参数配置如表6所示。

表6 VMD超参数配置Tab.6 Configuration of VMD super parameters

表7与表8分别为3种不同算法在不同数据集间的RMSE与MAPE的比较。实验中VMDSF-CSLSTM和VMD-CSLSTM、EMD-CSLSTM对比在多个数据集上具有更小的误差。特别是在SA4月份与7月份的电力负荷短期预测任务中VMDSF-CSLSTM的误差大于VMD-CSLSTM，这可能是由于VMDSFCSLSTM算法的拟合过程中，对那一组样本的拟合不够，或者说都是使用的同样参数的VMDSF-CSLSTM，而不是在SA训练集上寻找的模型最优参数。尽管如此，VMDSF-CSLSTM的表现还是稳定的，偏差在可接受范围内。

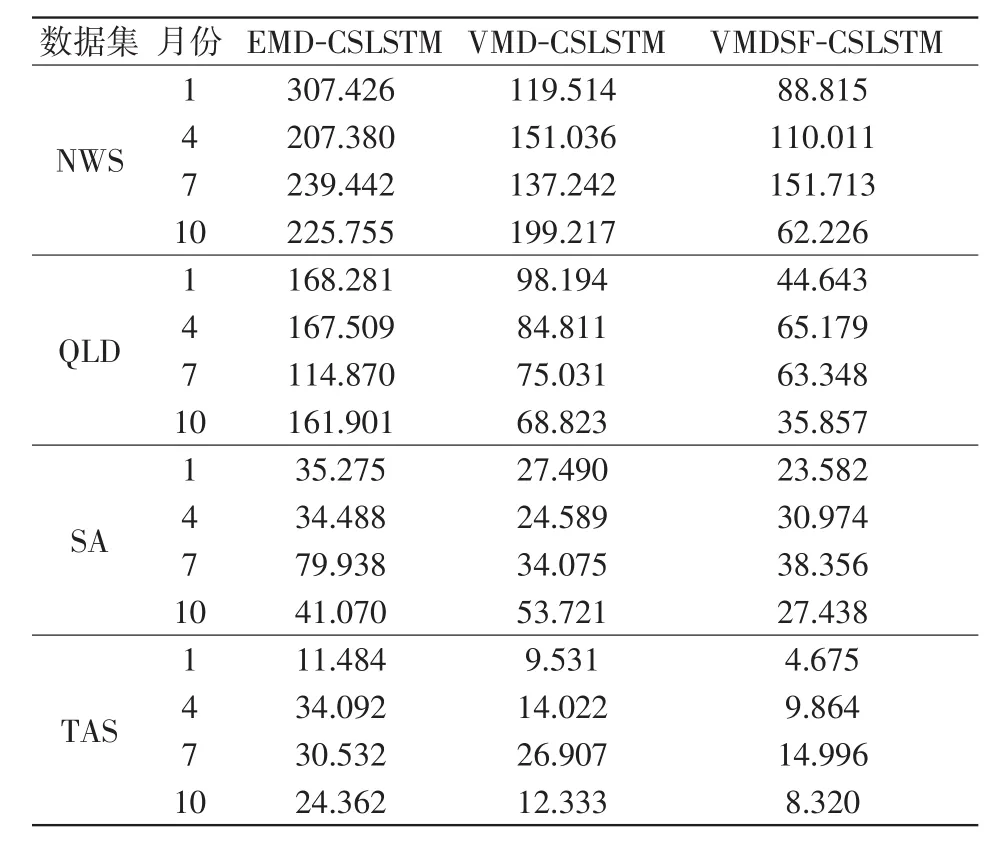
表7 各模型在不同数据上的RMSE比较Tab.7 Comparison of RMSE of different data among different models

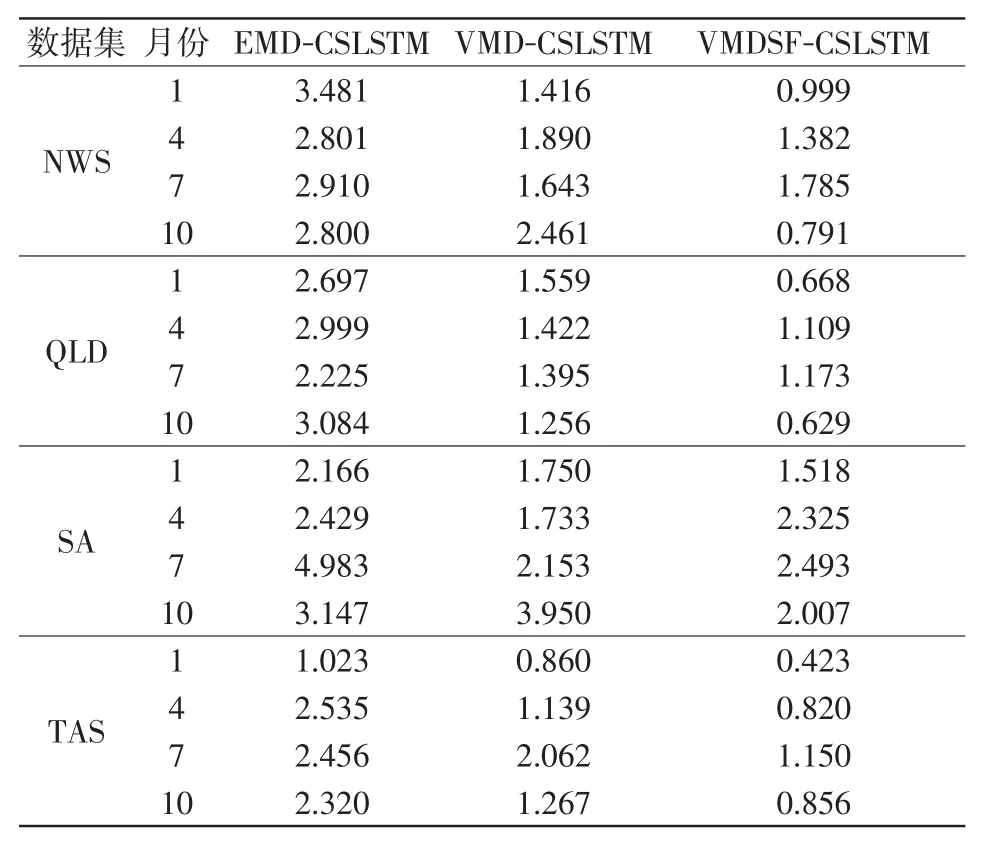
表8 各模型在不同数据上的MAPE比较Tab.8 Comparison of MAPE of different data among different models

为了更直观地看出本文所提的VMDSF-CSLSTM的模型效果，图10用折线图直观表示了该模型与VMD-CSLSTM、EMD-CSLSTM在各数据集上的实际48点短期电力负荷拟合情况，VMDSF-CSLSTM相比于其他两种对比组合模型，预测值更贴近实际值，预测效果更好，其平均百分误差MAPE达到了1.25%，与VMD-CSLSTM和EMD-CSLSTM相比分别提高了28.2%和54%。并且综合第二部分实验，可以证明VMDSF-CSLSTM在电力负荷预测上的有效性。

图10 VMDSF-CSLSTM的预测结果与其他模型对比Fig.10 Comparison of prediction results between the VMDSF-CSLSTM model and other models

3 结语

本文提出了一种基于快照反馈的短期电力负荷组合预测方法，通过VMDSF将原始电力负荷序列分解成多个子序列。随后，结合网格搜索法对CSLSTM网络进行最优参数寻找，得到含有最优模型参数的电力负荷短期预测模型。最后，使用VMDSF-CSLSTM组合预测模型，实现对负荷的准确预测。实验结果表明：本文所提出的方法不仅能够对电力负荷的变化趋势进行准确预测，对负荷的局部细节也有较高的预测精度；对比其他常见单一预测方法及常见组合方法预测精度、速度均有明显的提升，是短期负荷预测的一种有效方法。