基于人工免疫聚类算法的配电网故障状态相似性分析方法

董文娜，王增平，赵 乔，李钰洋，辛忠良，陈玉蛟

（1.新能源电力系统国家重点实验室（华北电力大学），北京 102206；2.国网河南省电力有限公司郑州供电分公司，郑州 450006）

配电网故障恢复是指当配电网发生永久故障时，通过网络重构完成对失电负荷的供电恢复，故障恢复对实现电网自愈性、提升供电质量具有重要作用。现阶段的配电网供电恢复决策主要采用在线运算的方式，通过某种智能算法生成转供电方案[1]。在电网规模扩大、负荷供电要求严格的环境下[2]，这种在线运算的方式将愈发难以满足快速恢复供电的需求。免疫系统是生物体内高度复杂的自适应智能系统，近年来，蕴含在其中的诸多免疫机制被广泛应用到工程领域中[3-5]。配电系统借鉴免疫系统的二次免疫应答思想，通过历史或仿真故障案例构建事故预案集，将部分需要在线完成的供电恢复决策运算安排在故障发生前完成，使之在故障发生后立即根据网络实际的故障状态匹配事故预案，调用预案知识指导系统进行故障恢复决策，能够提升故障恢复策略的生成速度。其中，配电网相似故障状态匹配是实现该项技术的关键。

近年来，不同领域的学者对网络相似性的度量开展了有益的探索。目前网络相似性的研究主要依靠度量拓扑相似度与聚类两个方向。度量拓扑相似度方法通过量化网络的拓扑相似度来评估网络的相似性。文献[6]以网络节点与边重复率为标准来评估网络的相似性；文献[7]计算由两个网络的各子网络邻接矩阵特征值构成的向量之差的二范数作为衡量网络相似性的依据；文献[8]以拓扑共享度为相似性指标，建立拓扑相似性函数量化两个网络的相似性；文献[9]将邻接矩阵奇异值作为相似性分析指标，利用可靠性已知的配电网计算出与其相似的配电网可靠性。量化拓扑相似度方法选取的相似性评价指标仅对拓扑进行描述，而不结合具体应用领域，难以综合反映相似网络的特征。另一种网络相似性分析思路是对拓扑结构进行聚类分析，根据某种距离计算规则将相似网络划分到同一类。文献[10]依据节点间点不重复路径对网络进行聚类；文献[11]基于对配电网结构、运行特点以及规划工作的实际需要，将配电网拓扑结构进行概念聚类，用于指导配电网规划问题；文献[12]对配电网络从宏微观方面建立拓扑特征集，通过分层聚类实现配电网拓扑相似性分析。聚类方法依据样本的自身特性对样本进行相似性划分，文献[10-12]结合具体应用领域提出相应的聚类依据，选取的指标能够较为全面地描述对象特征，但未对聚类初值对聚类效果的影响进行分析。

上述研究主要涉及配电网的规划与可靠性评估领域，面向不同网络的相似性分析，而故障状态相似性分析则面向同一个网络不同故障状态下的供电恢复。相似故障状态定义为某些故障状态下故障恢复策略具有较强的相似性，因此，应面向故障恢复策略的生成特点构建故障相似特征指标体系。

针对上述问题，本文首先在分析供电恢复策略影响因素的基础上，构建对故障样本集相似性分析的特征指标体系；其次，鉴于聚类分析能够根据样本自身特征通过某种相似性度量方法对样本集进行分类，在分析了不同聚类模型的基础上，建立人工免疫聚类算法。该模型将免疫算法中的某些机制引入到k-means算法中，能够弥补k-means聚类算法因对初值敏感易陷入局部最小值的不足。

1 配电网故障相似特征指标集的构建

在对样本进行聚类之前，需建立能够概括具有相似供电恢复策略的一类故障状态的特征指标集。配电网供电恢复策略实质上是操作单个或一组联络开关，由备用电源实现对非故障失电区域负荷的转供，供电恢复策略的生成主要与失电负荷大小、失电负荷分布情况及各源点的备用容量相关。因此本文将加权失电负荷量、各联络开关备用容量以及失电负荷-源点最短距离作为描述相似故障状态的特征指标。

1.1 失电负荷量

失电负荷量是指考虑负荷等级之后的等效失电负荷。故障发生后恢复非故障区域失电负荷的供电是供电恢复的主要目标，因此，失电负荷量是指导供电恢复策略生成的主要依据。失电负荷量主要由负荷等级和负荷大小两个因素决定，其计算公式为

式中：ci为负荷i的等级系数；nl为失电负荷数；PNi为负荷Pi经归一化处理后的标准值，且PNi∈[0，1]，其计算公式为

式中：Pi为负荷i的有功功率；Pmax与Pmin分别为网络中最大、最小负荷功率。

1.2 联络线备用容量

联络线备用容量表示的是各源点到与失电区域相连接的联络开关最短路径上的额定功率与负载功率差额的最小值。该指标表征了各供电馈线对失电负荷的供电能力，若某条馈线的备用容量较大，则往往选择闭合该馈线与失电负荷路径上的联络开关实现供电恢复。因此，联络线备用容量是指导供电恢复策略生成的一个重要指标。

首先，利用潮流计算求出每条支路的实际电流值；其次，从故障位置处开始通过广度优先搜索算法找到与其他馈线相联系的联络开关，并通过Floyd算法求出源点到与失电区域相连的联络开关的最短路径；最后，求出此最短路径上的额定电流值与实际电流值的差值中的最小值，其计算公式为

式中：B为转供电路径上所有线路的集合；INi为线路i的额定电流；Ii为流过线路i的实际电流值；IM(s)为馈线s的备用容量，数据处理方式同式（2）。

若两种故障状态下各变压器母线对失电负荷的供电能力情况相似，则二者在生成供电恢复策略时倾向于选择用该联络线去恢复非故障区域供电，即表明这两种故障状态很大程度上具有相似性。

1.3 失电区域-源点最短电气距离

失电区域-源点最短电气距离指的是变电站母线到失电负区域最短供电路径。配电网中供电路径延长往往伴随着网络损耗增加以及电压质量下降等问题，在其他变电站能给所有失电负荷均匀供电的情况下，这些因素将对供电恢复策略的生成起指导性作用。

电源s的失电区域-源点最短电气距离包括从源点到联络开关的最短距离DS以及从故障位置到联络开关的最短距离DF的两部分。首先，以故障发生线路的末节点作为父节点，通过广度优先搜索算法逐层搜索失电区域的联络点，并通过Floyd算法求出故障位置到联络点的最短距离DF；其次，由故障馈线的联络点出发，反向搜索可给失电区域进行转供电的馈线，并计算出该馈线源点到联络点的最短距离DS。电源s的失电区域-源点最短电气距离计算公式为

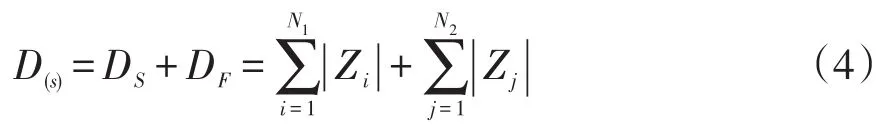
式中：N1为源点到联络点最短路径上的支路条数；N2为故障支路末节点到联络点最短路径上的支路条数；Zi、Zj分别为支路i、j的线路阻抗。

若某条馈线与失电区域不存在转供电路径，则该馈线的失电区域-源点最短电气距离视为无穷大。因此，本文选用logsig函数将数据进行归一化处理，如式（5）所示。

2 基于人工免疫聚类算法的故障相似状态匹配方法

故障形态相似性判断问题可转化为考虑如何将相似故障状态划分到同一类别中。目前分类方法有人工智能领域中的神经网络、Boosting等以及机器学习领域中的聚类分析。前者属于有监督的分类学习方法，而聚类是一种无监督学习方式，训练样本的标记信息是未知的，目标是通过对无标记训练样本的学习来揭示数据的内在性质及规律，为进一步的数据分析提供基础。而故障形态相似性判断中故障样本的所属类别事先无从得知，即输入样本属于无标记样本。因此，选用聚类方法解决配电网故障状态相似性判断问题。

按聚类准则不同，聚类算法可分为基于模糊关系的聚类算法和基于目标函数的聚类算法[13]。后者应用最广，本质是将聚类问题归结为优化问题。对于优化聚类目标函数的算法，一般都采用梯度法求解极值，而梯度法的搜索方向总是沿着能量减少的方向，使得算法很容易陷入局部最小值，对初始中心点位置敏感是基于目标函数的聚类算法的一大缺点。免疫优化算法[14]采用全局搜索和局部搜索相结合的方法，对初始状态不敏感，不容易陷入局部极小值，因此，将免疫优化算法与k-means聚类算法相结合，建立人工免疫聚类算法可弥补普通kmeans聚类算法的不足。

2.1 目标函数的构造

人工免疫聚类算法旨在将无标记的样本故障网络进行分类，将配电网故障恢复策略相似的样本归纳成一个类型的子集，而故障恢复策略没有共性的样本则被分离。分类的准则是同类样本间距离尽可能小，而不同类样本间距离尽可能大，以此来提高该模型的聚类质量。在此基础上，本文采用以离散度矩阵构造目标函数，不仅能反映同类样本间的聚集程度，而且能反映不同类样本之间的分离程度。

（1）定义类型i的离散度为

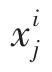
（2）定义类内离散度为

（4）定义类间离散度为

式中：mi为类别i的样本中心点；mˉ为各样本的特征指标均值。

为了提高聚类质量，要求类内离散度越小越好，类间离散度越大越好。因此，本文以式（9）作为人工免疫聚类算法的目标函数，即

该目标函数同时考虑了类内的离散度和类间的离散度，显然，fT值越大，则聚类效果越好。

2.2 人工免疫聚类算法的设计

利用人工免疫聚类算法求解问题的流程如下。

（1）输入初始化数据。如配电网络的网络结构、节点信息以及支路信息、聚类簇数k以及亲和系数α等。

（2）随机生成样本。通过随机选取o处故障位置及y种负荷变化情况，生成o×y个样本故障网络。

（3）样本特征指标集。计算出每个o×y个样本故障网络的失电负荷量、馈线的可供电功率、失电区域-源点最短电气距离，构建样本特征矩阵XN×(2s+1)。其中，N=o×y，而s为配电网络的馈线条数。

（4）编码方式。设定抗体ci是一个一维行向量，每h位代表一个样本中心点。其中，h=2s+1。人工免疫聚类算法的核心就是通过免疫机制调整样本中心点的位置，以弥补k-means算法对初始值敏感的不足。

（5）目标函数的确定。本文以式（9）作为目标函数。

（6）初始抗体种群的产生。随机产生R个初始子代群体，即R×k个初始样本中心点。

（7）计算每个个体的适应度。

b.由式（7）和式（8）计算个体的类内距离 SI和类间距离SB。

c.由式（9）计算出每个个体的目标函数 fT。

（8）免疫浓度机制。免疫浓度机制控制和调节抗体的增殖方向，以确保搜索方向的多样性，防止局部极大化。当抗体针对抗原有较高的亲和度时，该抗体就增殖；当这个抗体的增殖浓度过高时就被抑制，即当某几种分类方式极其相似且数量较多时，则该分类方式就应该被抑制。浓度概率的基本公式为

式中，pd为当抗体按浓度大小降序排列时的第t个个体的浓度概率；M为抗体总数。

抗体的浓度计算步骤如下。

a.采用Euclidean距离横向抗体u和抗体v之间的结合强度，其定义为

式中：q为基因长度；q×k为抗体长度；ui、vi分别为抗体u和v的基因，依据第2节所述方法对ui、vi进行数据处理。

b.Auv是抗体u和v之间的亲和力，定义为

式中，Huv为抗体u、v之间的结合强度，当Huv=0时，u和v的基因完全匹配，此时Auv=1。

c.抗体浓度是指某抗体及其相似抗体在群体中所占的比例，即

式中，λ为亲和力常数，一般取（0.9，1.0）。

（9）变异算子。此处采用均匀变异算子，其操作过程如下：首先，依次指定抗体编码串中每个基因作为变异点，即将样本中心点的每一位作为基因变异点；然后，对每一个变异点以变异概率pm从对应基因值的取值范围内取一个随机数来代替原有基因值。

（10）群体更新。将第（9）步得到的N个个体作为下一代进化的初始群体。

（11）终止条件。终止条件设为两次迭代适应度函数结果差值小于某个阈值时就停止迭代。若不满足终止条件，更新进化代数计算器，t=t+1，返回步骤（5）；若满足终止条件，则输出最佳个体，算法终止。

故障状态相似性分析流程如图1所示。

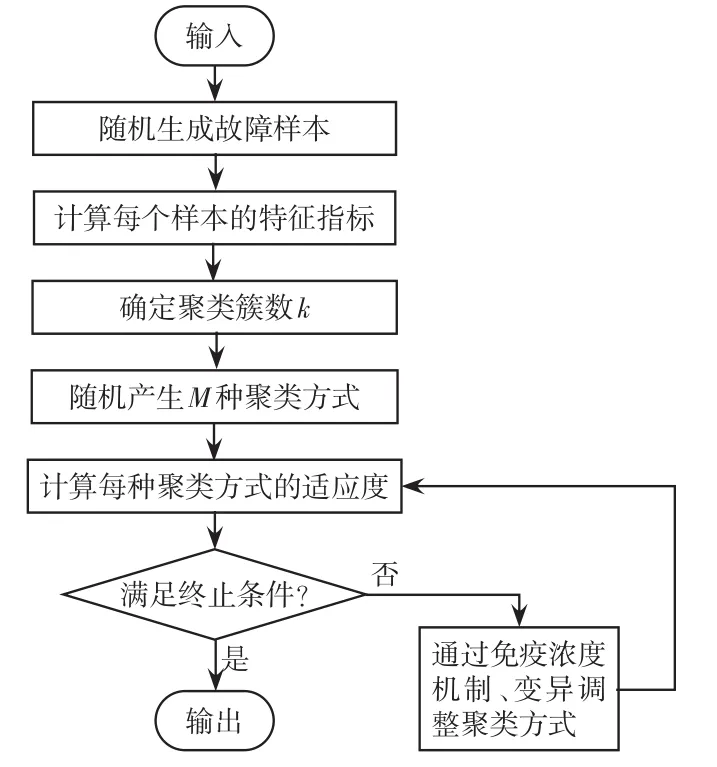
图1 故障状态相似性分析流程Fig.1 Flow chart of fault state similarity analysis

2.3 k值的选取

人工免疫聚类算法基于k-means聚类算法实现其功能，但k-means聚类算法需人为确定聚类簇数k，k值的选取将影响聚类效果。k值越大样本被划分得越精细，然而对于实际工程应用的借鉴价值则被大打折扣，因此在聚类之前要先确定“性价比”较高的k值。

“手肘法”是国际最常用于确定k值的方法，它的核心是误差平方和SSE（sum of squared errors）。

式中：Cj为第j个簇；rc为Cj中所有样本点；ci是Cj的样本中心；SSE为所有样本的聚类误差，反映了聚类的效果。

手肘法的核心思想是随着聚类簇数k的增加，样本会被划分得更加精细，每个簇的聚合程度会逐渐提高，则误差平方和SSE自然也随之减小。当k小于真实聚类数时，随着k的增大SSE大幅下降，而当k趋于真实聚类数时，再增加k所得到的聚合程度回报会迅速变小，因此SSE的下降幅度骤减，随后趋于平缓，也即，SSE与k值的关系曲线是一个手肘的形状，而肘部对应的k值就是较为理想的聚类簇数。

3 算例分析

本文以IEEE5馈线配电系统为例进行故障形态相似性分析。该配电系统有5条变电站母线，即有5个供电单元，网络节点总数为39，包含34个负荷节点，支路38条，其中有4条支路以联络开关连接。IEEE 5馈线配电系统如图2所示。

图2 IEEE5馈线配电系统Fig.2 IEEE 5-feeder distribution system

由于在实际配电网中对联络开关的操作次数极少，配电网的网络结构变化并不频繁，而故障位置以及负荷波动均具有随机性，因此，在生成故障样本网络时由随机算法选取20条故障支路仿真故障发生，并随机生成30种负荷变化情况模拟配电网运行方式的改变，由此随机生成20×30=600个故障样本网络，如表1所示。其中，已排除无法由其他馈线进行转供电的故障支路。

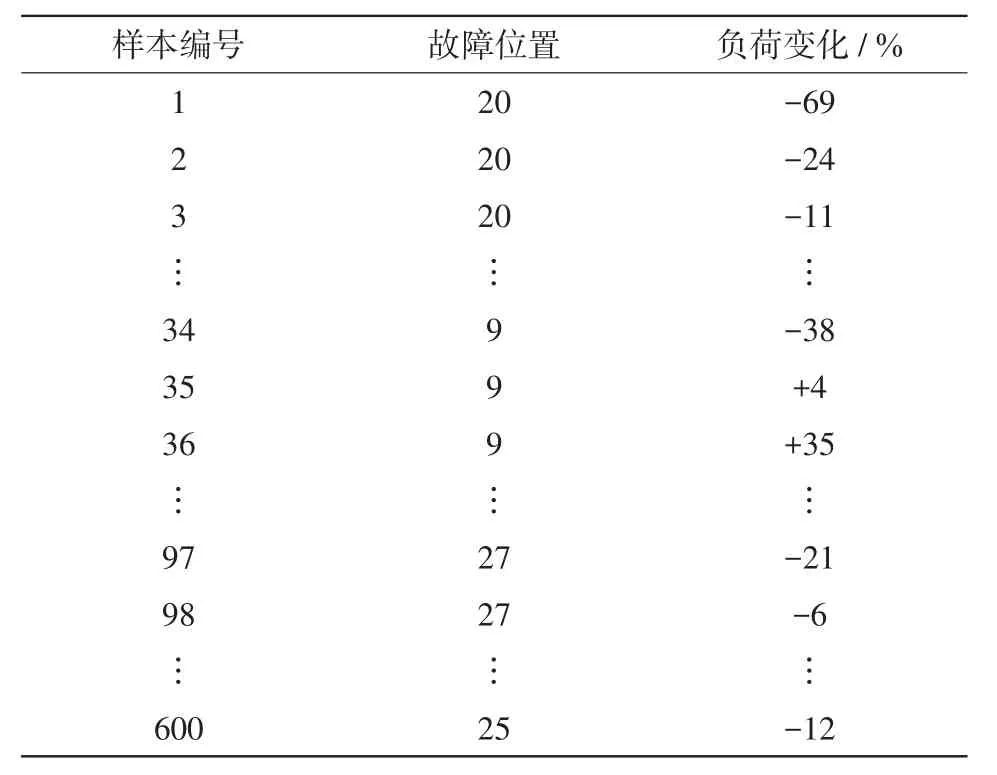
表1 故障样本网络集Tab.1 Fault sample network set

3.1 故障样本网络特征指标值的计算

由第1节所述方法，依次计算600个样本网络的失电负荷量、联络线备用容量以及失电区域-源点最短电气距离，结果如图3、图4和图5所示。

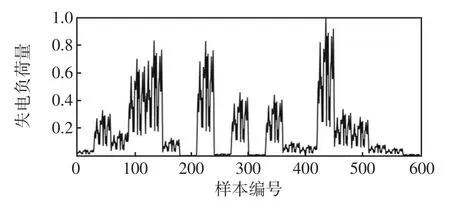
图3 故障样本网络的失电负荷量Fig.3 Power loss load of fault sample network

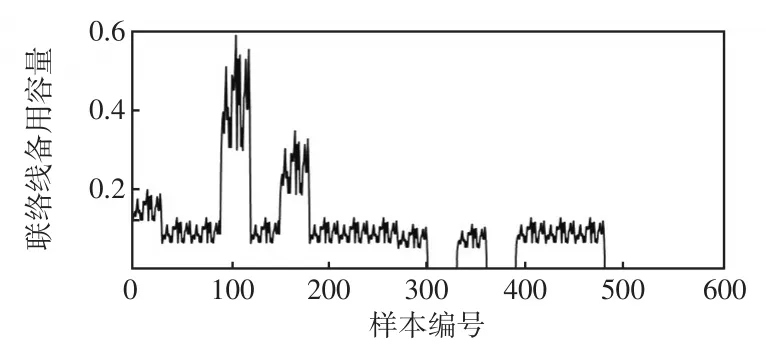
图4 故障样本网络的联络线备用容量Fig.4 Reserve capacity of tie line for fault sample network

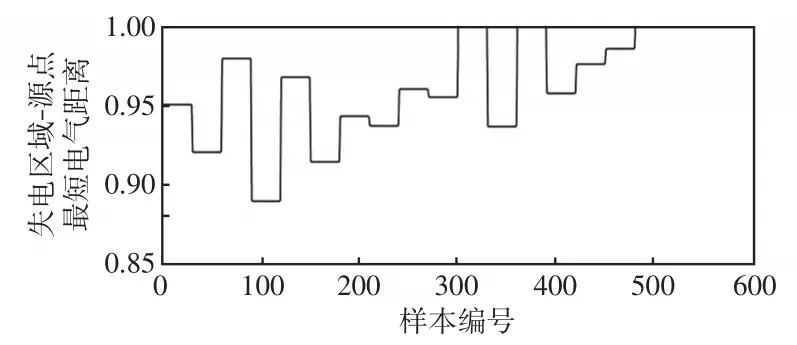
图5 故障样本网络的失电区域-源点最短电气距离Fig.5 Shortest distance between power loss area and source point of fault sample network

3.2 k值的选取

由手肘法确定聚类的簇数，其中，SSE与k值的关系如图6所示。

图6 SSE与k值的关系Fig.6 Relationship between SSE and k

显然，k取5时是算例中故障样本网络的最佳聚类簇数。

3.3 聚类结果

确定聚类簇数为5后，对表1中的600个故障样本网络进行聚类，图7是聚类结果的三维展示，距离度量方式采用的是欧氏距离。

图7 故障样本网络的聚类结果Fig.7 Clustering results of fault sample network

由表2的聚类结果可以看出，在IEEE5馈线配电系统中，正常负荷波动对聚类结果影响较小，配电网故障恢复策略主要取决于故障发生位置。

表2 各类别中包含的样本编号以及故障支路Tab.2 Sample numbers and fault branches included in each category

表2中，故障发生在支路7、9、27、30、31、32、33时所对应样本归为一类，分析图2可知，当这些支路发生故障时，若仅操作一次联络开关，则对其失电区域进行转供电的均为馈线3。支路24、26发生故障时，在联络开关操作一次的情况下，为其失电区域转供电的为馈线1。仿真验证和理论分析共同说明被划分到同一类别中的故障样本的供电恢复策略相似程度较高，可以互相借鉴。

3.4 聚类效果

在聚类算法中，通常选择轮廓系数作为聚类性能的评估指标。图8、图9分别是k-means算法各样本的轮廓系数以及人工免疫聚类算法各样本的轮廓系数，可以看出，前者在[-0.2，0.8]范围内波动，而后者主要在[-0.2，1.0]范围内波动。表3列出了kmeans算法与用于人工免疫聚类算法的算法的平均轮廓系数的比较。可见，人工免疫聚类算法比kmeans聚类算法在聚类效果上更具优势。

图8 k-means算法各样本的轮廓系数Fig.8 Contour coefficients of each sample in k-means algorithm

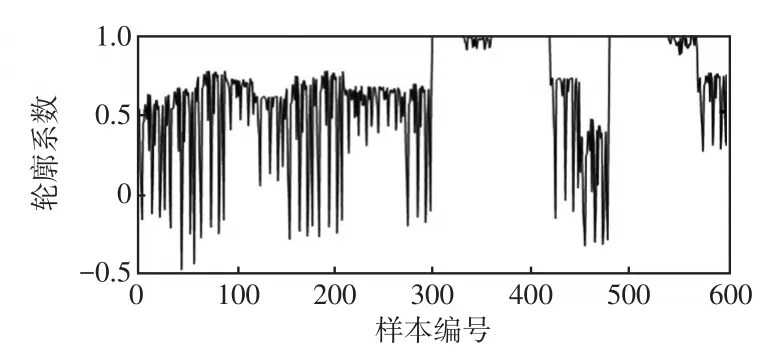
图9 人工免疫聚类算法各样本的轮廓系数Fig.9 Contour coefficients of each sample in artificial immune clustering algorithm

表3 平均轮廓系数比较Tab.3 Comparison of average contour coefficient

4 结论

为实现事故预案的匹配，加快供电恢复策略的生成速度，本文提出了一种基于人工免疫聚类算法的配电网故障状态相似性分析方法，所得结论如下：

（1）首先从影响供电恢复策略制定的因素入手，提取失电负荷量、馈线的剩余供电容量以及失电负荷到源点的距离作为故障网络相似性评定的特征指标，当某条馈线的剩余供电容量大于等于失电区域的失电负荷量，并且距离失电区域较其他馈线都近，通常选择闭合该馈线与失电区域的联络开关实现供电恢复；

（2）通过将免疫算法中的免疫浓度机制、变异机制引入到k-means算法中，使聚类中心点的调整方向更加多样性，从而避免了k-means算法因对初始中心点选取不当而造成聚类效果不理想的问题；

（3）仿真验证表明所提出的配电网故障状态相似性分析方法表征配电网故障状态的相似性，对供电恢复策略的匹配具有借鉴价值。