中段弹道目标分离过程动态散射特性分析
赵锋 徐志明 吴其华 艾小锋
(国防科技大学电子科学学院电子信息系统复杂电磁环境效应国家重点实验室 长沙 410073)
1 引言
弹道导弹作为一款“杀手锏”武器,具有飞行距离远、作用范围大、反拦截能力强等众多优点。面对弹道导弹的威胁,以美国为首的军事强国开始着力发展弹道导弹拦截系统。弹道导弹中段飞行距离最长,为了延长预警时间,提高拦截成功率,目前各国发展弹道导弹拦截技术的重点均放在中段[1,2]。在中段飞行过程中,弹道导弹会经历整流罩分离、弹头与母舱分离,释放诱饵等事件。由于中段大气阻力可以忽略不计,弹头、母舱、诱饵、碎片等目标会形成一个“目标群”,给弹道目标的跟踪[3,4]、识别和拦截带来了极大的挑战。
当弹头、诱饵、母舱分别位于不同的距离单元,利用弹头的雷达散射截面积(Radar Cross Section,RCS)序列[5],微动特性[2,6],高分辨率雷达图像[7],极化特性[8,9]对目标进行分类识别的技术已经较为成熟。当多个目标位于同一个距离单元,在对目标进行识别之前,多个目标的分离是至关重要的。目前,针对中段弹道群目标的目标分离、参数估计和识别已经展开初步研究。针对中段群目标的分离,空军工程大学张群教授团队[10,11]提出了在距离像序列构成的图像域上利用形态学滤波、骨骼提取和滑窗跟踪技术分别提取群目标微多普勒曲线的方法。西安电子科技大学刘宏伟教授团队[12]将时频分布上微多普勒曲线看作运动航迹,并利用航迹追踪算法分离出了多分量的微多普勒曲线。冯存前教授团队[13–16]研究了基于离散正弦调频变换、时频图像背景差分、正交匹配追踪算法、时频域联合滤波等多微动目标的时频曲线分离方法。涂世杰等人[17]将独立成分分析与模糊支持向量机相结合,对群目标的雷达回波进行分离并实现了真实弹头的有效识别。
上述研究均将群目标看作多个独立目标的组合,未考虑目标之间的电磁耦合现象。实际场景中,如图1所示,在弹头与母舱的分离过程前期,两目标距离较近构成紧邻结构,电磁耦合现象明显,不能简单看作两个独立目标的组合。如果将电磁耦合看作目标分离的“信标”,就可以及时集中雷达资源,检测、跟踪和识别由于分离过程产生的多个目标,筛选威胁系数较大的中段弹道目标,避免“跟丢”和“跟错”现象。因此,动态散射特性的研究对于中段弹道目标分离过程至关重要。本文针对窄带预警雷达探测背景下中段弹道目标3种分离方式的动态散射特性进行了深入分析,总结出了一般规律,优选出RCS均值、极化比、特征角、对称角等可以判断目标分离事件发生的特征量,为以后针对中段弹道目标分离过程动态散射特性的研究奠定了基础。
2 中段弹道目标动态散射计算模型
如图2所示,本文选取的电磁计算模型为锥柱组合结构,锥体和柱体的高度分别为0.5m和0.6m,底面半径为0.15m,材料为金属。为了实现中段弹道目标分离过程的动态计算,控制柱体结构沿z轴的负方向移动。每移动一次,利用多层快速多极子(Multi-Level Fast Multipole Algorithm,MLFMA)进行静态电磁计算。锥柱组合体为旋转对称目标,目标的散射响应与方位角无关,因此电磁计算的角度扫描设置为:方位角φ=0°;俯仰角θ=0°~30°,角度步进θ为0.2°。其中方位角定义为与x轴的夹角,俯仰角定义为与z轴的夹角。电磁计算的频率设置为3GHz。电磁波入射方向的极化基(H,V)定义为式(1)。

图2 中段弹道目标结构示意图Fig.2 Structure of mid-course ballistic targets
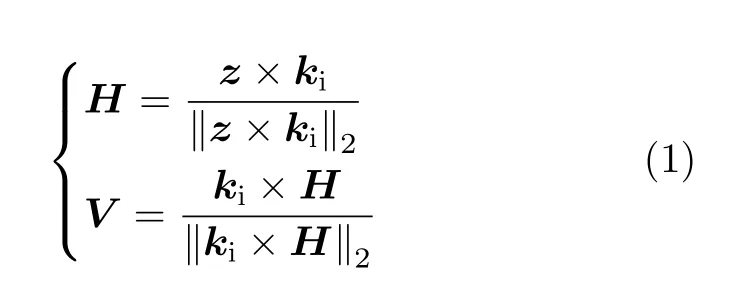
其中,‘×’代表向量的叉乘运算;ki为电磁波入射方向的单位向量;‖•‖2为向量的模。
如图3所示,为了模拟中段弹道目标实际的分离过程,分别采用3种方式控制柱体向后移动。分离方式A:锥体与柱体分离,柱体单纯往下平移;分离方式B:锥体与柱体分离,柱体往下平移过程中,以y轴为旋转轴匀速旋转,在该分离过程中,xOz平面一直为锥体和柱体的对称平面;分离方式C:锥体与柱体分离,柱体往下平移过程中,以x轴为旋转轴匀速旋转,在该分离过程中,xOz平面仅在特殊时刻同时是锥体和柱体的对称平面。3种分离方式柱体向下移动的距离单位均为0.05m,分离方式B和分离方式C中柱体每次旋转的角度单位均为9°,旋转中心为柱体轴线的中点。3种分离方式共执行移动201次,对应的距离变化范围为0~10m,柱体共旋转5圈。
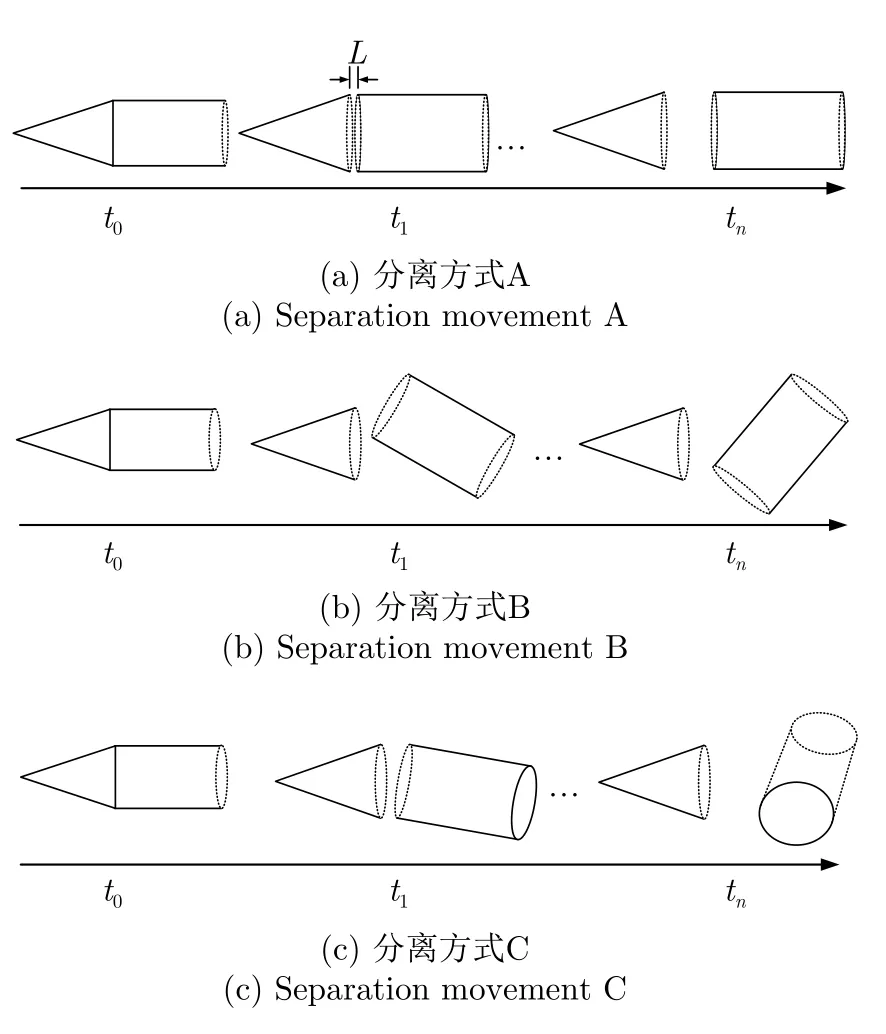
图3 锥柱组合体目标3种分离方式示意图(纸面代表图2中的xOz平面)Fig.3 Three types of separation movements for cone-cylindershaped ballistic targets(xOzplane in Fig.2coincides with the paper)
3 中段弹道目标分离过程动态散射特性分析
本节首先分析了中段弹道目标分离过程动态RCS分布的“形态”以及直观的规律,然后从RCS均值、极化比、特征角、对称角几个参数的角度分析了其在分离过程中的变化规律,为以后的分离过程提供判别的量化指标。
3.1 动态RCS分布
图3中3种分离方式下,锥柱组合体的动态RCS分别如图4—图6所示。图中三维的坐标分别是电磁波入射角度,锥柱组合体分离距离和RCS的对数值。
从图4可以看出,在分离方式A条件下,锥柱组合体的动态RCS变化在电磁波方向维度波动较大,而随着目标的分离,RCS的起伏较小。此时,锥柱组合体的RCS改变主要取决于中段弹道目标的运动引起相对雷达的姿态角变化。根据雷达极化学可知,由于随着目标的分离,极化参考平面xOz同时是锥体和柱体的对称平面,因此交叉极化一直很弱,理论值为0。
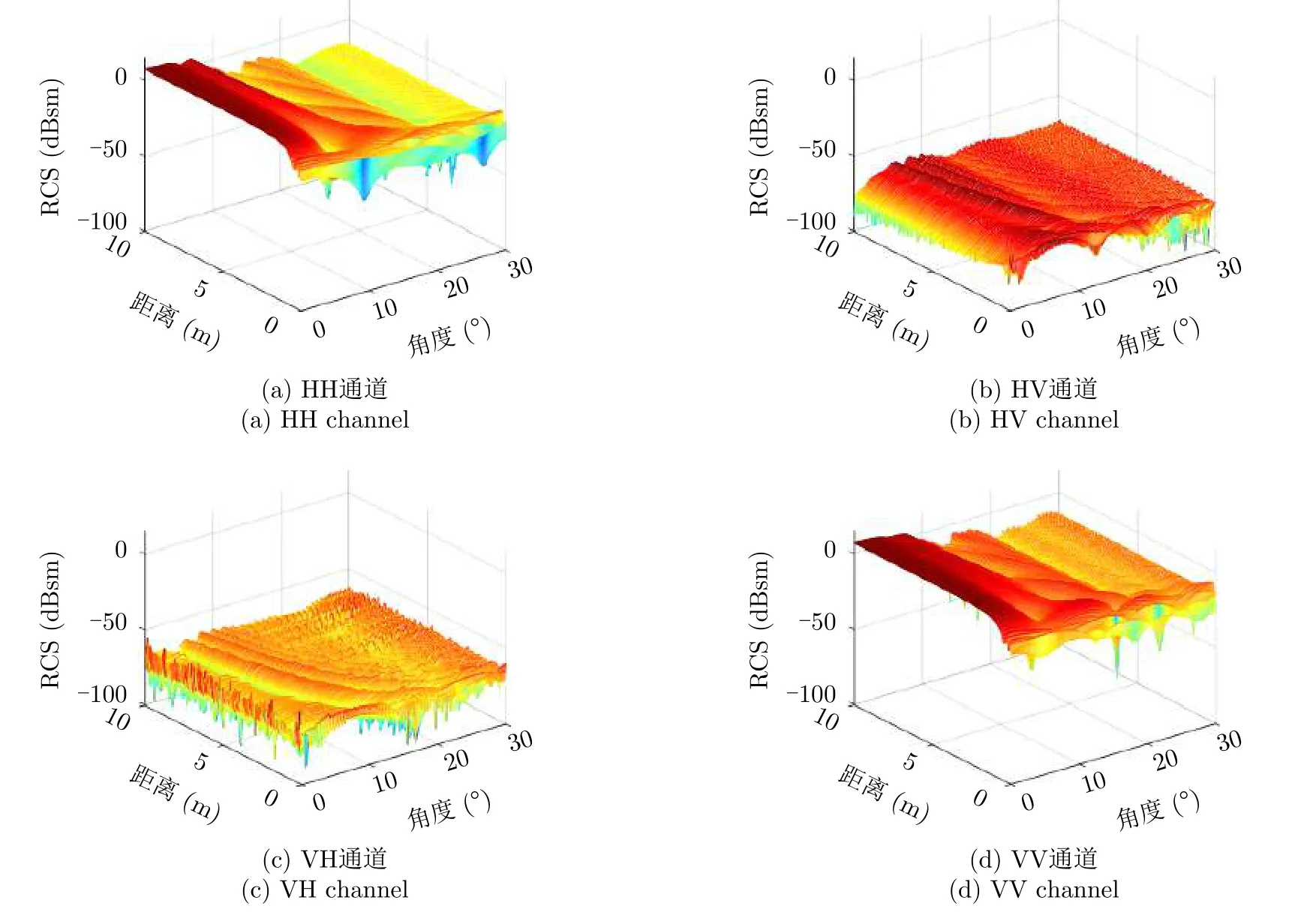
图4 锥柱组合体分离方式A动态RCS分布Fig.4 Dynamic RCS distribution of cone-cylinder-shaped targets with separation movement A
从图5可以看出,在分离方式B条件下,由于柱体在向后的运动过程中还存在翻滚运动,锥柱组合体RCS随着目标分离起伏剧烈,而此时目标相对于雷达姿态改变引起的RCS改变则相对显得“平缓”。虽然柱体在向后的分离过程中引入了翻滚运动,但是与分离方式A相同,极化参考平面xOz同时是锥体和柱体的对称平面,因此交叉极化响应仍很弱,理论值为0。

图5 锥柱组合体分离方式B动态RCS分布Fig.5 Dynamic RCS distribution of cone-cylinder-shaped targets with separation movement B
从图6可以看出,分离方式C最明显的特征是交叉极化响应增强。锥柱组合体的交叉极化和主极化响应的强度均随着锥体和柱体的分离起伏剧烈,且交叉极化响应的峰值与主极化响应的峰值交错分布。

图6 锥柱组合体分离方式C动态RCS分布Fig.6 Dynamic RCS distribution of cone-cylinder-shaped targets with separation movement C
3.2 目标分离事件特征
(1)RCS均值
为了衡量中段弹道目标RCS在分离过程中的动态变化,对每次分离状态下俯仰角θ=0°~30°范围内的RCS进行数学平均,RCS均值的定义为

其中,N为总的角度点数。
3种分离方式的RCS均值在中段弹道目标分离过程中的动态变化如图7所示。图7(a)中分离方式A的RCS均值变化较为“缓和”,从目标分离开始到锥体与柱体相距20λ,主极化RCS均值整体趋势是变大,增幅约20dB;锥体与柱体相距20λ~100λ以后,两个目标之间的电磁耦合效应可以忽略不计,因此总的RCS趋于稳定。符合随着目标结构变复杂,RCS增大的认知。
引入柱体的翻滚运动后,分离方式B主极化RCS均呈现较大的起伏。分离方式B中存在两种“特殊”目标状态:“状态1”是当柱体旋转到母线与电磁波方向垂直时,柱体的侧面发生镜面反射,RCS很大;“状态2”是当柱体的轴线和锥体的轴线共线时,状态相当于分离方式A,由于锥体和柱体的边缘绕射,RCS较大。柱体旋转1圈,会存在2次“状态1”和2次“状态2”。在本文的中段弹道目标动态散射计算模型中,柱体共旋转了5圈。因此,图7(b)中出现了20个RCS峰值,其中高的峰值对应“状态1”,矮的峰值对应“状态2”。
分离方式C的RCS变化规律与分离方式B类似,也存在同样的两种“特殊”目标状态。不同的是分离方式C中极化参考平面xOz仅在特殊时刻才同时是锥体和柱体的对称平面,因此分离方式C的交叉极化响应不再是0。两种特殊的状态对应共极化RCS的峰值,交叉极化的零点。
(2)极化比
从RCS均值的分析中可以看出,极化信息可以反映目标分离的丰富信息。其中共极化与交叉极化响应的幅度之比是目标的一个重要极化特征。本小节主要分析了极化比随目标分离的变化过程。如图7所示,后向散射满足互易性,即SVH≈SHV;中段弹道目标表面光滑不存在类似偶极子这种具有极化取向的结构,主极化通道近似相等,即SHH≈SVV。所以,极化比由SHH/SVH计算得到

图8给出了锥柱组合体中段弹道目标3种分离方式下极化比的统计结果。从图8(a)可以看出分离方式A的极化比随着目标的分离成递增趋势,与图7(a)中RCS的均值变化规律相吻合,极化比的增大主要得益于主极化RCS的增大,而交叉极化随着目标的分离近似不变;同样的道理,图8(b)的极化比变化规律也是与图7(b)相对应的。由于分离方式3中交叉极化响应不再是0,所以极化比的下限小于前两种分离方式20dB。在特殊状态下,共极化的峰值对应于交叉极化响应的零点,所以极化比形成“尖峰”,使得极化比的变化规律呈现独特的“梳子型”。可以利用极化比的这种变化规律判断中段弹道目标分离事件是否发生。
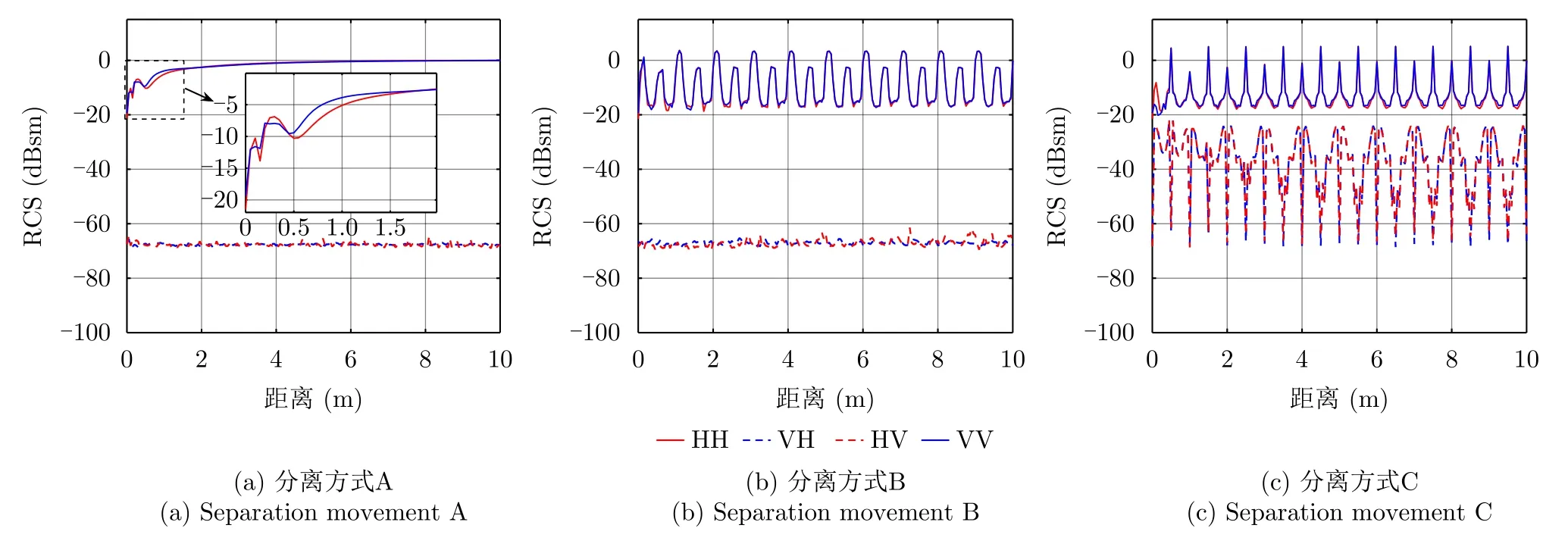
图7 锥柱组合体RCS均值随着目标分离的变化Fig.7 Mean variation of RCS for cone-cylinder-shaped targets with separation movements

图8 锥柱组合体极化比(SHH/SVH)随着目标分离的变化Fig.8 Polarization ratio variation of cone-cylinder-shaped targets with separation movements
(3)对称角和特征角
根据Huynen经典的雷达极化学理论,散射矩阵S可以对角化为
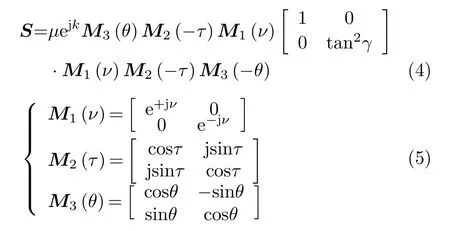
θ取向角,τ对称角,ν跳跃角和γ特征角是Huynen目标参数集。µ和k分别代表幅度和绝对相位,与目标的极化散射特性无关。τ对称角,ν跳跃角和γ特征角是与目标绕雷达视线旋转无关的物理量。τ反映了目标的对称性,当τ=0时,目标关于某个平面是对称的;ν反映了目标的奇偶次散射情况,ν=0对应奇次散射机理,ν=π/4对应偶次散射机理;γ衡量了目标的“变极化”能力,γ=0时,目标的散射波极化与入射波极化无关(例如偶极子结构);γ=π/4时,目标的散射波极化与入射波极化相同。Huynen目标参数集取值范围为

经过筛选,对称角和特征角两个极化特征随目标分离会出现有规律的变化,将每个分离时刻所有视线的对称角和特征角进行平均得到图9和图10。如图9所示,3种分离方式下,特征角均接近π/4,反映了中段弹道目标结构简单、表面光滑,不存在类似偶极子结构等类型的部件。分离方式B和分离方式C中当电磁波视线与柱体母线垂直时会发生镜面反射,对于镜面散射机理,特征角会接近π/4,因此在图9(b)和图9(c)中特征角随目标分离均出现离散的峰值。分离方式A仅作理论对比分析,实际场景中不会存在分离方式A的情况,更多是分离方式B和分离方式C的组合,因此利用特征角的这种“梳子型”变化规律可以判断分离事件是否发生。
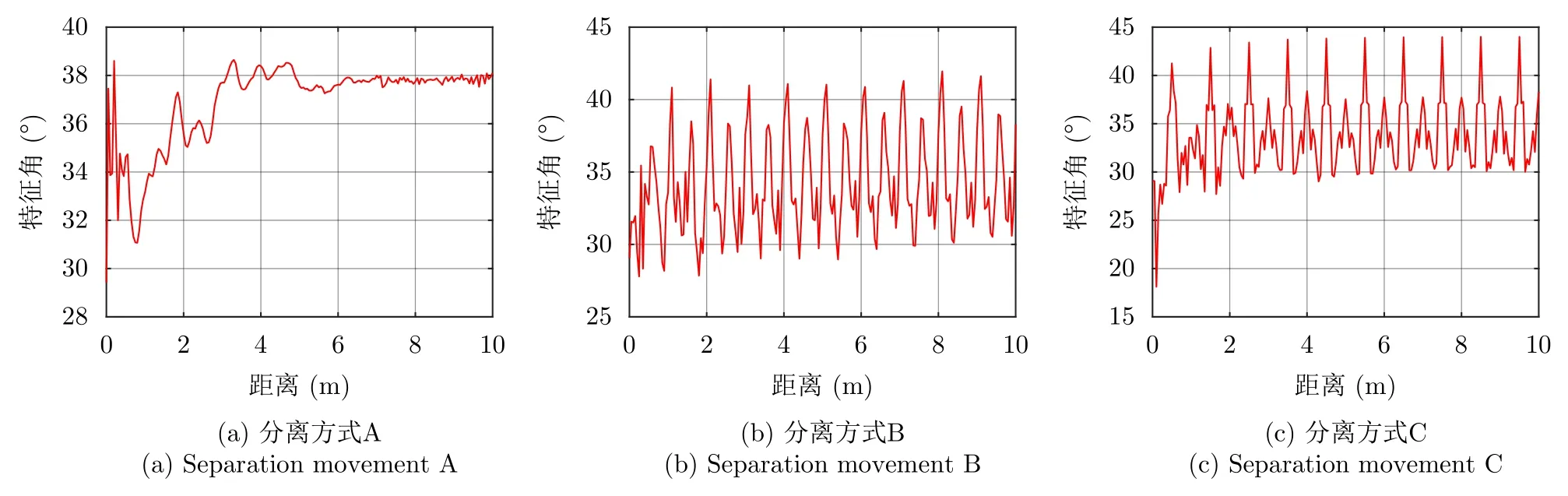
图9 锥柱组合体特征角随着目标分离的变化Fig.9 Characterization angle variation of cone-cylinder-shaped targets with separation movements
对称角反映了目标的对称性,对称目标对应τ=0。锥柱组合体目标是旋转对称的,因此,对称角的理论值应为0。分离过程中,分离方式A和分离方式B中雷达视线一直位于锥体和柱体的共同对称平面内,因此提取的对称角τ=0,如图10(a)和图10(b)所示。分离方式C中雷达视线仅在特殊时刻会同时位于锥体和柱体的对称平面内,提取的对称角τ开始偏离0。由于考虑空气动力学等因素,中段弹道目标通常会设计成近似旋转对称结构,因此分离前对称角通常会接近0;当分离事件发生后,母舱、诱饵等目标缺乏姿态控制结构,分离产生的多目标结构很难满足τ=0的条件,开始在0附近震荡,可以当作判断分离事件发生的特征。
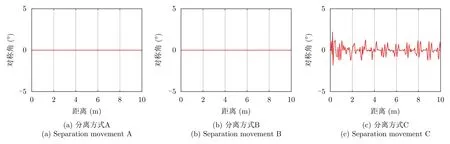
图10 锥柱组合体对称角随着目标分离的变化Fig.10 Symmetry angle variation of cone-cylinder-shaped targets with separation movement
为了验证所提出的分离事件特征在噪声条件下的鲁棒性,对入射角度(θ=15°)时空间目标分离过程中的动态RCS数据添加噪声,然后从噪声背景下的RCS序列中提取分离事件特征,并进一步比较噪声背景下每项分离事件特征表征空间目标分离事件能力的强弱。从空间目标分离过程中的动态RCS分布可知,空间目标RCS的起伏随着视线角的变化是慢变的,所以仅选取θ范围的中值15°进行分析。
对入射角θ=15°,锥柱组合体分离过程中的动态RCS序列添加SNR=15dB的白噪声,得到全极化RCS、极化比、特征角和对称角如图11—图14所示。从图11—图14可以看出,噪声对于提出的分离事件特征具有一定的影响。图11中对应于“状态1”的RCS峰值由于数值较大,仍然保持了较大程度的起伏;对应于“状态2”的RCS峰值则淹没在了噪声中。图12中对应于分离方式B的极化比由于受到噪声的影响不再像图8中具有明显的“梳子型”形状特征,而变得杂乱。同样,图13中对应于分离方式B和分离方式C的特征角的“梳子型”形状特征也被破坏,只是随着柱体的翻滚运动而快速起伏变化。与前三者比较而言,对称角表现得受噪声影响较小,对应于分离方式A和分离方式B仍然保持数值0;分离方式C的对称角较图10中的结果起伏更加剧烈,更好地反映了其分离规律。
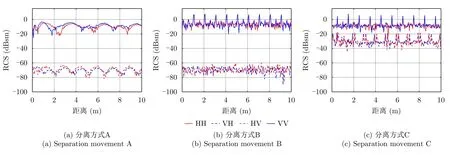
图11 锥柱组合体RCS随着目标分离的变化(θ=15°)Fig.11 RCS variation of cone-cylinder-shaped targets with separation movements(θ=15°)

图12 锥柱组合体极化比随着目标分离的变化(θ=15°)Fig.12 Polarization ratio variation of cone-cylinder-shaped targets with separation movements(θ=15°)
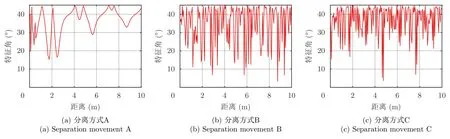
图13 锥柱组合体特征角随着目标分离的变化(θ=15°)Fig.13 Characterization angle variation of cone-cylinder-shaped targets with separation movements(θ=15°)
为了定量衡量4种特征表征空间目标分离特性的强弱,采用序列的7个指标均值、极差、标准差、变异系数、平滑度、偏度系数、峰度系数[18]构建分离事件特征序列的特征向量其中i表示分离方式i=A,B,C;p为分离事件特征索引,p={RCS、极化比、特征角、对称角}。分别求得图11—图14中3种分离方式的4个分离事件特征序列的特征向量如表1所示。

表1 空间目标分离事件特征的定量化表征Tab.1 Separation accident features characterization for space targets
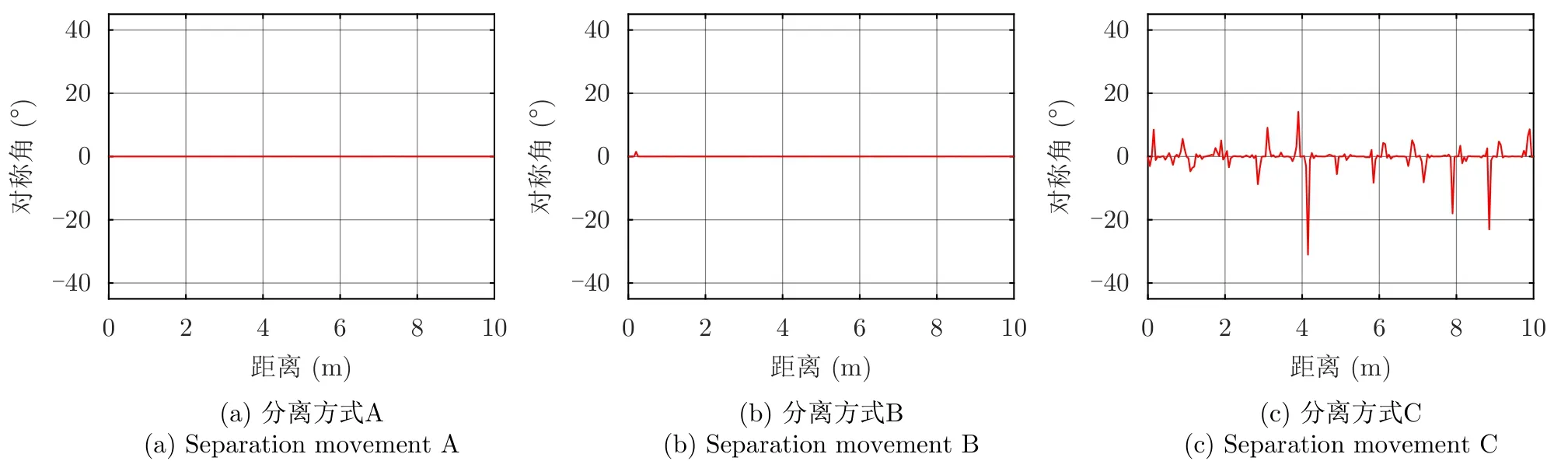
图14 锥柱组合体对称角随着目标分离的变化(θ=15°)Fig.14 Symmetry angle variation of cone-cylinder-shaped targets with separation movements(θ=15°)
利用式(7)分别求得用每一个分离事件特征表征3种分离方式时两两之间的“隔离度”,如表2所示。从表2可以看出,任何一个分离事件特征都难以将3种分离方式完全划分清楚。例如,由极化比隔离度可以看出,利用极化比特征可以很好地区分分离方式C和分离方式A或B,却难以区分分离方式A和B;利用主极化RCS序列可以很好地区分分离方式A和分离方式B或C,却对区分分离方式B和分离方式C的能力较弱。这说明对于判断空间目标分离事件的发生,不能依赖单一的特征,需要综合利用多种特征。由于引入噪声的影响,图13中的特征角序列呈现的“梳子型”规律发生较大变化,对于表征3种分离方式的差异性能力较弱。相比之下,噪声背景下的对称角仍然保持未加噪声时的变化规律,因此对于区分分离方式C和分离方式A或B的能力较强。
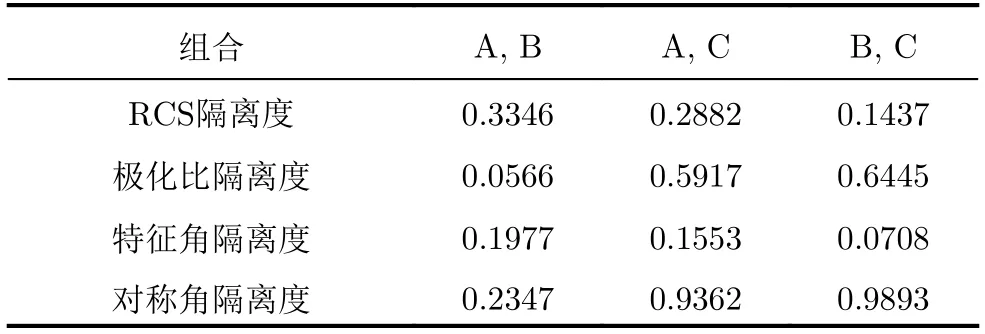
表2 不同分离方式之间的隔离度Tab.2 Isolation measurement between separation movements characterization features
4 结论
本文重点关注了中段弹道目标分离阶段前期,多个目标之间在分离过程中的电磁耦合散射特性分析。在此基础上,分析了优选的RCS均值、极化比、特征角和对称角4个特征量在目标分离过程中的动态变化,为判断中段弹道目标分离事件是否发生提供依据。目前,该研究关注的仅是早期预警雷达对中段弹道目标进行预警探测时的窄带场景,后续研究会进一步讨论宽带情况下中段弹道目标分离过程的动态散射特性,并进一步丰富与分离事件关系紧密的特征量。

