基于序列图像的航天器自主导航降维滤波方法

2021-07-05 13:46孙博文王大轶王炯琦周海银葛东明董天舒

航空学报 2021年4期

孙博文，王大轶，王炯琦，周海银，葛东明，董天舒

1. 国防科技大学文理学院，长沙 410073 2.中国空间技术研究院北京空间飞行器总体设计部，北京 100094

空间飞行器在轨服务与维护是航天技术领域的重要发展方向，是延长卫星、平台、空间站等空间飞行器寿命和能力，减少卫星运行成本的重要保证，对我国航天领域的发展具有重要意义[1-4]。

在轨服务对象大多属于“非合作目标”，比如，① 未安装辅助测量标识的空间飞行器，② 无法向外传输自身信息的空间飞行器，③ 由于故障等原因失效处于自由运动状态的空间飞行器，④ 空间碎片等等[5-8]。空间机器人利用机械臂抓捕空间非合作目标时，为减小操作过程中与非合作发生碰撞的风险，精准快速地估计非合作目标的运动状态是前提和基础，即空间机器人和空间非合作目标之间相对运动状态的估计[9-12]。

通常情况下，执行在轨服务与维护的卫星通常携带双目相机对非合作目标进行立体视觉观测，依据图像信息，选取非合作目标若干特征点，从而构建特征点观测坐标系。然而，对于空间自由运动的物体，其姿态运动学模型均在非合作目标本体坐标系下构建，但通过双目相机的观测值无法直接解算出非合作目标本体坐标系，一般采用扩展卡尔曼滤波算法对非合作目标姿态进行高精确估计。国内外学者为此做了大量研究工作[13-17]。

Segal等[18]在状态变量中估计一组特征点在非合作目标本体坐标系下的位置，通过跟踪目标特征点的方式，并利用迭代扩展卡尔曼滤波观测模型来估计相对位置，姿态，旋转和平移速度。在实验中利用最大后验识别方案确定最可能的惯性张量，无需在滤波中估计惯性比。考虑到基于光照对视觉的影响，Peng等[19]提出了一种基于激光雷达和双目相机的非合作目标姿态估计方法，该方法能够适应恶劣的光照条件，且具有较好的鲁棒性和较高的精度。但是星上资源有限，无法进行高负荷运算同时也无法携带过多测量设备。

Aghili和Parsa[20]提出了一种自适应噪声的卡尔曼滤波方法，状态变量包括相对位置速度，姿态四元数，非合作目标相对惯性系的角速度，自身惯量比，非合作目标本体坐标系与特征点观测坐标系的位置与姿态关系等。为了避免滤波发散，将四元数估计变为对四元数误差的估计。Zhang等[21]针对翻滚航天器提出了一种相对位置和姿态的估计方法，采用了一般偏心轨道相对方程描述相对位置动力学，并将状态变量扩展为主副航天器相对于轨道系的四元数，得到了较为精确的结果。

为了不损失测量新息，Ge等[22]在状态变量中加入非合作目标特征点在非合作目标本体坐标系下的位置矢量进行估计，测量值加入非合作目标特征点在相机系下的位置矢量，并进行仿真实验，表明该方法具有较高的实际应用价值。然而，以上方法都存在待估状态变量维数高，从而影响状态滤波收敛速度的问题，进而影响空间飞行器的在轨服务与维护。

针对这一问题，本文提出了一种基于序列图像的非合作目标相对导航方法，该方法由两个滤波算法组成，首先不需要考虑非合作目标的位置变量，仅对非合作目标的姿态进行精确估计，然后在非合作目标姿态估计的基础上对非合作目标的相对位置与速度进行估计。本文在非合作目标自由运动满足的姿态运动学模型基础上，依据双目相机测量原理，分别分析了非合作目标姿态、相对位置速度与测量的关系，构建了基于序列图像的测量模型，分别建立了不含有非合作目标质心位置的状态方程和基于非合作目标位置、速度矢量的状态方程，并利用扩展卡尔曼滤波对非合作目标的状态变量进行估计。数学仿真实验表明，本文提出的方法可以在50次采样之内收敛，同时可以得到高精度的姿态估计结果。

1 双目相机测量原理

观测卫星携带双目相机对目标进行观测。如图1所示，两相机平行放置，构成平行式立体视觉模型。假设相机系Oc-xcyczc原点位于左相机光心处，yc轴指向相平面中心，xc轴平行相平面指向右相机，zc轴构成右手坐标系。两相机内部参数一致，焦距为f，基线长度为b。当观测特征点P时，假设特征点P在左右两相机相平面成像坐标分别为(ul,vl)和(ur,vr)，由三角形几何关系可以得到

图1 双目相机测量示意图Fig.1 Schematic diagram of binocular stereo vision

(1)

则在相机系下特征点P的坐标向量为[22]

在观测卫星利用双目相机对非合作目标进行观测时，可同时观测多个特征点。由于非合作目标为空间中小天体、非合作卫星或天空垃圾等等，可以看作刚性物体，故各个特征点在非合作目标本体坐标系的相对位置矢量不变，所以由特征点构造的坐标系相对于非合作目标本体坐标系的姿态不随非合作目标运动而改变。由两组不同特征点构造的坐标系之间的姿态也不随非合作目标的运动而改变，所以无妨假设双目相机可以一直观测某几个特征点(无法观测时也可根据特征点构造坐标系之间的相互转化实现)。下面介绍根据观测的特征点构造的特征点观测坐标系Om-xmymzm。

依据以上假设，选取非合作目标上的3个非共线的特征点P1,P2,P3，建立特征点观测坐标系Om-xmymzm。定义特征点观测坐标系原点位于P1点，xm轴方向为矢量P1P2方向，单位矢量为

(2)

zm轴方向为矢量P1P2和矢量P1P3所在平面的法线方向，故其单位矢量为

(3)

建立右手坐标系，则ym轴方向单位矢量为

ry=rz×rx

(4)

从而，可以得到相机系到特征点观测坐标系的姿态转换矩阵为

(5)

然而，对于翻滚状态的非合作目标，其姿态与非合作目标本体坐标系密切相关。如图1所示，坐标系OT-xTyTzT为非合作目标本体坐标系，通过双目相机观测非合作目标特征点并不能直接解算出非合作目标本体坐标系，但是由于双目相机观测的特征点在非合作目标本体坐标系的位置矢量为常量，所以非合作目标本体坐标系与特征点观测坐标系之间的姿态关系固定不变。

为了更好描述非合作目标的运动姿态(即非合作目标本体坐标系的姿态)，同时避免奇异性，本文采用四元数对姿态进行表述。故可以假设特征点观测坐标系相对于非合作目标本体坐标系的四元数为η，即η为常量。

2 基于立体视觉测量的目标姿态估计

2.1 四元数基础

定义非合作目标本体坐标系相对于惯性坐标系的四元数为

(6)

式中：该四元数表示为惯性坐标系绕单位矢量轴e旋转φ角度到非合作目标本体坐标系；qv、q0分别表示四元数的矢量和标量部分，记qv=vec(q)，易知四元数的模长为1。则用四元数表示惯性坐标系(用字母i表示)到非合作目标本体坐标系的旋转矩阵为

(7)

式中：S(qv)的表达式为

(8)

(9)

则有

q⊗q-1=q-1⊗q=[0,0,0,1]T

(10)

2.2 姿态运动学方程

假设非合作目标本体系主惯量分别为Ixx,Iyy,Izz，则定义惯量比l=[lx,ly,lz]T为

(11)

对于非合作目标，其主惯量与惯量比均未知。假设非合作目标本体坐标系相对于惯性系的旋转角速度在非合作目标本体坐标系下的表达式为ω=[ωx,ωy,ωz]T，则非合作目标做自由翻滚运动时的动力学方程为

(12)

非合作目标本体系相对于惯性系的四元数运动学方程为[23]

(13)

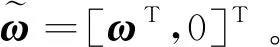
(14)

(15)

(16)

(17)

(18)

2.3 测量方程

当相机对非合作目标进行观测得到如式(5)所示的姿态旋转矩阵时，可得到特征点观测坐标系相对于相机系的四元数qr为[12]

(19)

μ=qr⊗qc

(20)

假设特征点观测坐标系相对于非合作目标本体坐标系的四元数为η，非合作目标本体坐标系相对于惯性系的四元数为q，则

μ=η⊗q

(21)

根据文献[19]可知，针对四元数μ的矢量部分有

δμv=vec(δη⊗δq)

(22)

则分别对δqv,δηv求偏导可得[19]

(23)

2.4 滤波过程

定义扩展卡尔曼滤波的状态变量为

(24)

根据上述推导得到如下离散方程:

(25)

式中：δx为状态估计误差变量；εk、vk分别为过程噪声和测量噪声，分别满足均值为零，方差为Q和R的正态分布；测量值z为四元数δμ的矢量部分，即z=vec(δμ)；Φk、Hk分别为系统的状态转移矩阵和测量矩阵，表达式为

Φk=I12+AkT

(26)

式中：

(27)

(28)

下面给出滤波步骤：

步骤1利用四阶龙格库塔法根据式(13)和式(12)进行状态变量qv和ω的一步预测，状态变量l,η的一步预测取上一步的滤波值，即lk|k-1=lk-1，ηk|k-1=ηk-1。

(29)

步骤3状态变量协方差一步预测

(30)

步骤4计算增益矩阵

(31)

步骤5状态变量更新

(32)

(33)

(34)

(35)

(36)

(37)

(38)

步骤6状态协变量方差更新

Pk=(I12-KkHk)Pk|k-1

(39)

3 基于姿态的非合作目标位置估计

3.1 状态方程

图2为非合作目标相对位置示意图。坐标系Oc-xcyczc为观测卫星轨道坐标系，原点位于航天器质心，xc轴为观测卫星的向径方向并指向轨道外，zc轴为观测卫星轨道面正法线方向，yc轴构成右手坐标系。

图2 非合作目标相对位置Fig.2 Relative position of non-cooperative target

当观测卫星与非合作目标之间的距离远小于观测卫星轨道半径rs时，短期内可以利用C-W方程描述两者之间相对位置关系，在观测卫星轨道坐标系下表示为

(40)

(41)

设置采样时间间隔为T，则离散形式的C-W方程为

(42)

其中：

(43)

(44)

3.2 测量方程

简便起见，假设观测卫星轨道坐标系与相机系之间的旋转矩阵为单位矩阵，即两坐标系重合。

如图2所示，非合作目标质心在观测卫星轨道坐标系下的位置矢量为r，第i个观测点Pi在相机系下的位置矢量为ri，在非合作目标本体系下的位置矢量为ρi，假设观测卫星轨道坐标系相对于惯性系的四元数为qs，则非合作目标本体坐标系相对于观测卫星轨道坐标系的四元数qr为

(45)

则观测模型为

ri=r+R(qr)ρi

(46)

(47)

3.3 滤波过程

步骤2状态变量协方差一步预测

(48)

步骤3计算增益矩阵

(49)

步骤4状态变量更新

(50)

步骤5状态变量协方差更新

(51)

4 仿真验证

根据上述推导过程进行仿真验证。仿真数据如下设置：假设非合作目标主惯量分别为Ixx=10 300 kg·m2，Iyy=5 390 kg·m2，Izz=9 190 kg·m2，计算得到惯量比分别为lx=-0.368 9，ly=-0.205 9，lz=0.534 3。目标质心初始相对位置为[1,0.1,0.1]Tm，初始相对速度为[0.005,-0.001, -0.005]Tm/s，初始姿态四元数为0,0,0,1]T，初始角速度为[2,2,2]Trad/s，3个特征点在非合作目标体坐标系下坐标分别为[0.2,0,0]Tm，[0,0.2,0]Tm，[0,0,0.2]Tm，采样频率为10 Hz。