一种非规则采样航空时序数据异常检测方法
闫媞锦,夏元清,*,张宏伟,韦闽峰,周彤
1. 北京理工大学 自动化学院,北京 100081 2.北京航天自动控制研究所,北京 100070
航天器是极其复杂且昂贵的飞行器,具有数千个遥测传感器,详细记录了温度、辐射、功率、仪器和计算活动等方面的时序信息。一旦出现无法监测和响应异常状态的情况,航天任务很可能会失败。考虑到这些传感器数据的复杂性,如大量的缺失、噪声随时间推移而累积等,如何有效快速监控这些传感器的数据以监测航天器的运行状态是十分关键且重要的问题[1]。
当前多维时序异常检测方法因其广泛的应用场景而备受关注。常见的异常检测方法可分为3类[2-3]:基于统计的方法、基于机器学习的方法和基于深度学习的方法。当前航天器遥测数据的异常检测主要为基于统计的方法,如差分整合移动平均自回归(ARIMA)模型、基于局部加权回归散点平滑法的周期和趋势(STL)分解、小波变换等,用于指示何时偏离预定范围,专家系统[4-5]也已经成为少量航天器状态监测的重要方法。但上述方法有较大的局限性,例如无法快速处理大量数据、耗费人力且需要专家信息等。而基于机器学习的方法主要包括聚类[6]、贝叶斯学习[7]等,但这类方法无法建立多维时序数据维度间的依赖关系;而基于深度学习的方式则是当前较为活跃的研究领域。其中,基于监督学习[8-9]的方法在训练过程中由于需要标签信息,只能检测到已知异常类型,具有较大局限性,因此无监督方法[10-15]如今受到更多学者的关注。基于无监督的异常检测方法可分为以下两类:
第1类为确定性模型。为检测航空时序数据的异常,文献[8]采用长短期记忆网络(LSTM)对多维时序数据每个通道进行预测,并采用预测误差确定异常点;文献[13,16]采用基于LSTM的自编码器模型建模正常时序的分布,并采用重构误差判定传感器数据的异常。虽然LSTM相比于循环神经网络(RNN)更能建模长时依赖,但它是完全确定性的模型,缺乏鲁棒性,无法很好地处理噪声数据。
第2类为随机性模型。文献[17]同时结合高斯混合模型(GMM)和深度自编码器(DAE)并提出基于高斯混合模型的深度自编码器(DAGMM)模型;然而,它仅用于考虑多维变量而不是多维序列,无法考虑时序数据中的时序依赖。文献[12]结合对抗生成网络,采用博弈思想对正常数据分布进行学习。以往的工作表明,由于随机变量建模的方式可以学习时序数据的概率分布,其异常检测效果比确定性方法好。
此外,上述方法都是针对规则采样且缺失率较低的多维时序数据建模的。但航空时序数据往往会存在大量的缺失,甚至本身采样间隔就不是常值,上述方法便会失效。过去几年中,已提出了很多方法用于解决时序数据中的缺失问题[18-19]。一类直观的方法是填充法,例如平滑或插值法[20]、谱分析[21]、核方法[22]、多重插补法[23]和期望最大化(EM)算法[19]等。然而此类方法会导致整体流程的割裂,且都是基于某种假设对缺失数据进行填充,因此可能无法求得最优预测。
针对上述方法存在的问题,本文提出了非规则采样多维时序异常检测算法(Irregularly sampled Multivariate time series Anomaly Detection,IMAD)模型,针对非规则采样的多维航空时序数据,采用特殊结构的门控循环单元[24](Gated Recurrent Unit,GRU)建模,在模型层面解决缺失值及采样不规则的问题;此外,采用变分自编码器[25](VAE)引入随机性,建模正常时序数据的分布,提高鲁棒性,并采用重构概率[26]表明数据异常的概率;接着,根据极值理论[27]自适应确定合适阈值检测异常;最终,在两个真实航空时序数据集上进行实验,验证IMAD模型的有效性。
1 GRU模型与变分自编码器
首先,介绍用于时间序列数据建模的GRU基本形式以及变分自编码器的基本架构。
1.1 GRU模型
RNN对于序列数据建模具有较好的效果,每一时刻可以将其看为一个非线性状态空间模型,但它无法对时序数据的长时依赖进行建模。因此,LSTM和GRU相继被提出以解决此问题。相比RNN,GRU包含一个重置门rt和一个更新门zt控制隐藏状态ht,更新过程为
(1)
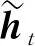
1.2 变分自编码器
变分自编码器是一种深度贝叶斯模型,它建立了两个随机变量x和z之间的联系。首先,假设z服从某先验分布p(z),如多元高斯分布,而后x由神经网络构成的条件分布pθ(x|z)中采样得到,其中下标θ代表神经网络中的参数,pθ(x|z)分布的具体形式根据具体任务决定;此外,由于真实的后验分布pθ(x|z)难以计算,VAE中采用变分推断的方式,用神经网络估计后验分布qφ(z|x),通常假设估计后验分布满足高斯分布N(μ(x),σ(x)),其中μ(x)和σ(x)为用神经网络计算得到的期望和标准差。最终,x的最大似然估计为
(2)
根据詹森不等式,可得
(3)
不等式式(3)右侧为变分下界,记为L。随机梯度变分贝叶斯(SGVB)算法是有效优化变分下界的一种方式。此外,蒙特卡罗采样法经常用于估计式(2)中的期望项,从而加快训练速度,本文中仍采用此方法。
2 问题定义
假设有一非规则采样且带有缺失值的多维航空遥测时序数据X=[x1,x2, …,xN],其中N为时序数据的长度,xt∈RD表示第t次的观测值为D维向量。由于时间跨度角度,采用步长为1的滑窗策略逐段进行异常检测,即xt-T:t∈RD×(T+1)为从第t-T~t次观测的序列,由于数据中具有较多缺失值,采用M=[m1,m2, …,mt]表示缺失值指示矩阵,并用Δ=[δ1,δ2, …,δN]表示由相邻两有观测值的时刻间隔δt组成的矩阵,其形状与输入X相同,st为第t个观测值对应的时刻,示例为

(4)
3 IMAD整体结构
如图1所示,IMAD算法异常检测的流程包括两部分:离线训练和在线检测。数据预处理为两部分共用模块。预处理模块的主要步骤包括将数据进行归一化,并对数据进行滑窗分段:

图1 IMAD算法异常检测流程Fig.1 Overall structure of IMAD for anomaly detection
(5)
式中:μx和σx分别为输入数据的期望及标准差。
在离线训练阶段,预处理过后的数据输入至模型训练,并输出每个观测值的异常分数,这些异常分数通过基于极值理论的自动阈值选择模块确定合适阈值,以便线上异常检测使用。此外,离线训练保存的模型通常会进行周期性的更新,从而能够持续学习输入数据分布的变化。在线上检测部分,首先加载离线训练中保存的模型,新观测的实时数据通过预处理模块后给到线上检测模块,从而得到新观测值的异常分数,一旦分数超过选定阈值,则报警给地面运维人员。
离线模型架构及训练策略将于4.1~4.3节中介绍,线上检测模块将于4.4节中介绍,而自动阈值选择模块则在4.5节中给出详细的策略。
4 方法设计
首先介绍处理非规则采样且带缺失值时序数据建模方法,然后给出离线模型的整体架构和训练方法,最后给出线上检测的方式和自动阈值选择策略。
4.1 非规则采样且有缺失值时序数据建模
式(1)的表达形式是建立在所有变量均可观测的前提下的,而对于存在大量缺失的情况,可在GRU输入前,对输入变量xt和隐藏状态ht加入可学习的时间衰减项:
(6)
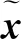
(7)
式中:Vr、Vz和V为因mt新增神经网络参数;xt和ht-1通过式(5)得到。图2展示了GRU与带有可训练迟滞项的GRU(GRU with trainable Decays)的不同之处,图中γx和γh分别为x和h的衰减因子。

图2 GRU与GRU-D对比Fig.2 Comparison between GRU and GRU-D
此外,采用以下3类GRU-D的变体作为非规则采样且有缺失值的时序建模的实验对比,用于证明GRU-D单元的有效性:
1) 假设在未观测时刻输入变量X保持不变,此类方法记为GRU-forward,此时对应的形式为
xt=mtxt+(1-mt)xt′
(8)
2) 用输入变量X的均值对缺失值进行填充,此类方法记为GRU-mean,此时对应的形式为
(9)
3) 将上述得到的变量X与缺失值指示矩阵M、观测时间间隔矩阵Δ连接起来,一同送入GRU中,此类方法记为GRU-simple。此类方法进一步考虑了时间间隔和缺失值位置,相比GRU-forward和GRU-mean利用了更多的信息。
4.2 模型架构
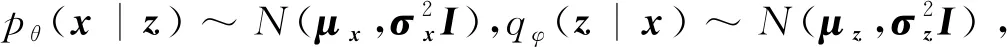
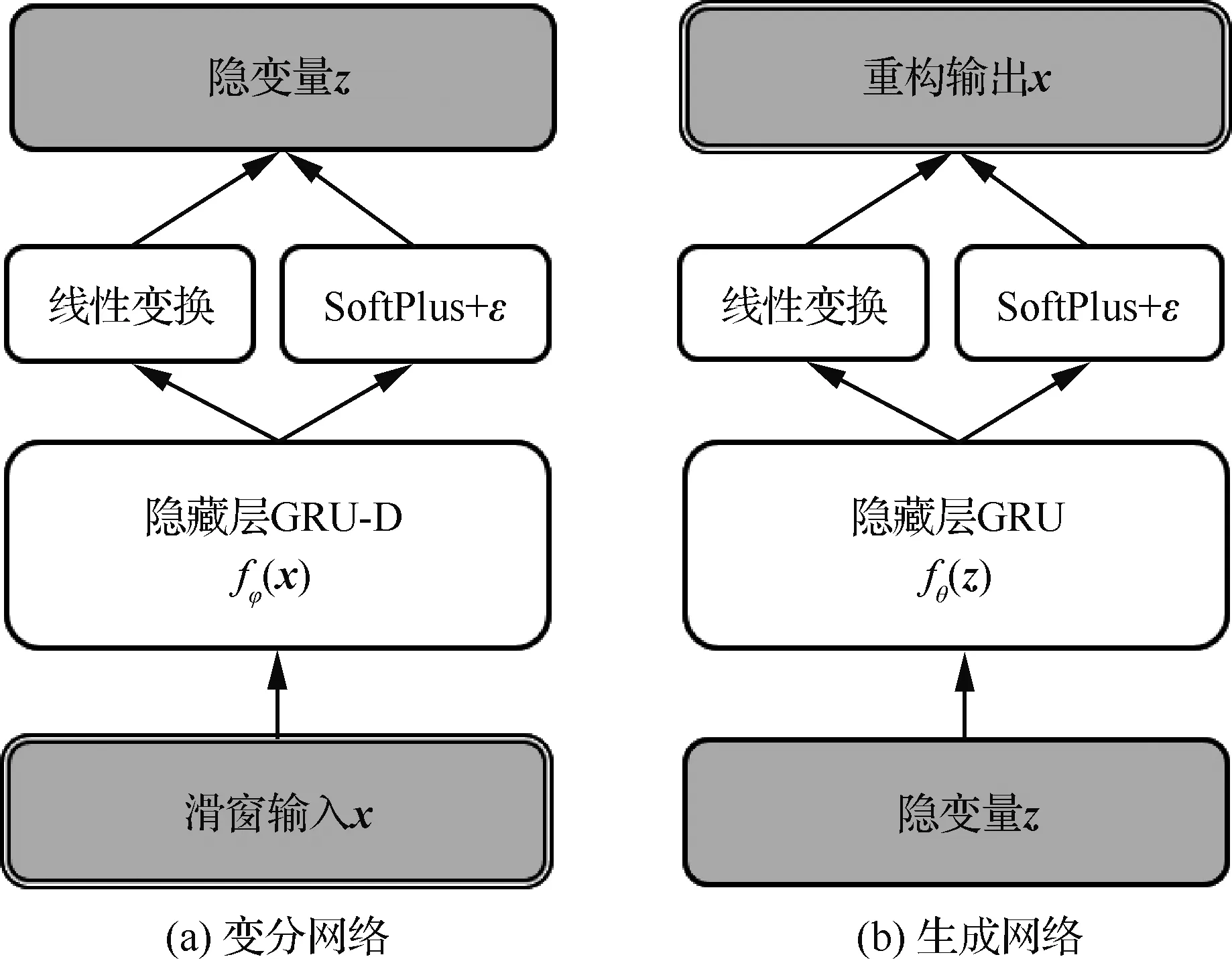
图3 时序异常检测网络结构Fig.3 Network structure for time series anomaly detection
(10)

4.3 训 练
训练采用SGVB算法直接优化式(3)中的下界,且文献[26]提到训练时蒙特卡罗采样每次采一个样本就足够。此外,训练时采用重参数化方法进行采样,即不直接从z~N(μ(x),σ(x))中采样,而是引入一个新的随机变量ξ~N(0,I),从而将采样z重写为z(ξ)=μz+ξσz。此时,每次采样仅需从标准正态分布中采一个样本,便可得到对应的采样z,这解决了采样操作不可导的问题,从而使其能像训练普通神经网络一样使用随机梯度下降训练变分自编码器。在训练中,训练数据每轮训练首先进行随机打乱,有利于随机梯度下降的优化。此外,应保证给到模型中的每批数据足够大,从而能使训练过程中的损失比较稳定。最终,考虑到缺失值的情况,模型的损失为
lg(pθ(xt-T:t|zt-T:t))M·S
(11)
式中:S为比例系数,S=size(M)/sum(M)。实际上,模型损失第3项可看作重构损失,而前两项恰好可以写成Kullback-Leibler(KL)散度的形式。S用于平衡损失中各项的大小,从而避免模型只注重学习重构项lg(pθ(xt-T:t|zt-T:t))而忽略了KL散度,进而解决了缺失数据引起的性能衰退问题。此外,与普通自编码器相比,VAE额外加入了KL散度,使得估计后验分布qφ(z|x)与假设先验分布pθ(z)之间的距离尽量小,此时重构输出的分布中对应的标准差不为0,从而能够用统计的角度判断输入变量的异常概率。
4.4 线上检测
模型训练完成保存后,可用于判断某一时刻的观测变量xt是否存在异常。由于模型的输入滑窗长度为T+ 1,根据文献[26]可知,VAE中可采用条件概率lgpθ(xt|zt-T:t)作为数据异常检测的评价分数,采用此重构概率作为异常分数St。异常分数越大,表明输入变量xt可以较好地重构,即若某观测变量符合输入变量的整体分布,则此观测变量能以较高置信度进行重构。反之,异常分数越小,代表重构输出和输入变量之间差距较大,即若异常分数St小于某阈值后,则输入变量xt被标记为异常,并告警给地面运维人员。阈值选择策略将会在4.5节中介绍。
4.5 自动阈值选择策略
在离线训练时,计算每个观测值的异常分数,最终可得到一个异常分数构成的序列{S1,S2, …,SN′},而后则可根据极值理论[27](EVT)自动选取合适的阈值。
EVT用于发现极端值的分布规律,而极端值一般都分布在概率分布的尾部。EVT的优点是它并不对数据做任何的前提假设,此外文献[27]还提出了POT(Peaks Over Threshold)算法,其基本思想是利用广义帕累托分布(GPD)拟合某概率分布的尾部极端值分布。因此,根据POT学习异常分数的阈值。由于小于此阈值的被认为是异常,因此,采用广义帕累托分布:
(12)

(13)
式中:N′为观测值的数目;N′th为满足S< th的数目;q为满足S 首先介绍两个真实多维航空时序数据集;而后给出评价指标,对比方法和实验参数设置;最后给出实验对比结果和分析。 土壤水分监测卫星时序数据集(SMAP)和火星科学实验室探测器“好奇号”时序数据集(MSL)是美国国家航天航空局的卫星公开时序数据集,其基本信息如表1所示。每个数据集分为训练集和测试集两部分,且两部分数据都有对应的标签。图4给出了SMAP中数据归一化后一些典型的异常数据段。可以看出SMAP数据不同阶段的数据分布特性具有明显差别,且不同通道之间数据互相影响,序列整体呈现高度非线性且缺失值较多的特性,因此这类时序数据的异常检测任务较为复杂。然而,遥测数据是地面运维人员监测航天器异常事件的重要工具。 表1 数据集基本信息Table 1 Dataset information 图4 SMAP数据集异常点示例Fig.4 Examples of anomalies in SMAP dataset 采用精准率(Precision)、召回率(Recall)和F1分数作为异常检测结果的评价指标,其中: (14) 由于以往一些方法有阈值确定方法,依然按照原来策略确定阈值;对于无阈值确定方法的模型,遍历可能的阈值找出F1分数最高时的指标F1best进行比较。实际上,异常发生往往会持续一段时间,因此只要在异常发生期间有报警,则认为此段异常能够正确报警。 首先,针对带有缺失值的多维时序数据异常监测任务,在模型框架不变的基础上,对比了GRU-D的模型的一些变体,用于证明GRU-D模型对带缺失值数据异常监测的有效性。然后,由于以往较少有做带有大量缺失值的多维时序数据异常检测工作,因此也对比了一些针对规则采样且缺失率较低的多维时序数据异常检测方法:基于变分自编码器的单维时序异常检测算法Donut逐通道进行异常检测,用于验证直接建模多维模型比逐维度异常检测效果好;带有非参数动态阈值策略的LSTM模型[1](LSTM-NDT)用于验证RNN和VAE结合的效果比只用LSTM的模型好;基于LSTM的自编码器模型[28](LSTM-AE)用于验证VAE异常监测的有效性;基于高斯混合模型的自编码器[17]用于验证RNN时序数据建模的有效性。 实验中设定滑窗长度为100,GRU-D的隐藏层维度为20,隐变量z的维度设定为3,每批数据大小设为50,训练迭代5次,在训练中采用Adam优化器,初始的学习率设定为10-3。此外,在训练阶段,将训练集拆分出30%的数据当作验证集,用于评估训练的程度,在训练中使用早停策略,防止模型过拟合。对于自动阈值选择模块,两数据集中满足异常分数小于阈值的期望概率q=10-4;此外,为了保证线下训练和线上运行的一致性,线下的阈值策略往往需要仔细设置,因此实验中,下分位数在0~0.07的范围内以训练集异常检测效果为指标进行启发式搜索,最终对SMAP而言,下分位数设定为0.07;对MSL而言,下分位数设定为0.01。所有方法实验中的随机数种子设定为3,均在24 G显存的泰坦服务器(NVIDIA GeForce RTX TITAN)上运行完成,所有结果均为同参数下运行10次的平均值。 分3个部分进行验证,首先,按不同比例随机丢弃一部分数据,并比较IMAD模型与其变体的异常监测效果;而后,与规则采样多维时序异常监测方法对比;最后,分析模型对于隐变量z的敏感程度。 5.3.1 IMAD模型与其变体对比 比较将IMAD模型中的GRU-D模块替换成其变体,保持实验参数不变,将两真实数据集按照0.1~0.5的比例随机丢弃进行实验对比,最终得到不同方法异常检测的F1分数随缺失率变化的对比。 由图5可知,GRU-D相比于其他变体方法的异常检测效果好,尤其是在MSL数据集上,在缺失率从0.1变化到0.5时,基于GRU-D的方法异常检测效果比其他所有变体都要好,证明带有可学习参数的指数衰减法相比直接用均值和最近时刻观测值的填充法更能有效建模带有大量缺失值的数据;单从模型表达效果随缺失率变化来看,随着缺失率的变化,基于GRU-D的IMAD模型的异常检测效果在小范围内波动,证明基于GRU-D模型的IMAD模型在含有缺失值的多维时序数据异常检测任务中具有较强的鲁棒性;而其他3种变体随着缺失率的上升,异常检测的F1分数值呈下降趋势。此外,基于GRU-simple的IMAD模型异常检测结果大体上比基于GRU-forward和GRU-mean的IMAD模型好,说明缺失值指示值及两相邻观测值时间间隔对于建模带有缺失值有重要作用。 图5 不同缺失率下模型性能对比Fig.5 Comparison of performance of models with different missing rates 5.3.2 IMAD模型与规则采样数据检测方法对比 对比IMAD模型与规则采样且缺失值较少的时序数据异常检测方法(Donut、LSTM-NDT、LSTM-AE以及DAGMM),由于这些方法并没有针对非规则采样且具有较多缺失值的时序数据进行建模,因此,用SMAP和MSL全量的数据验证上述模型的效果,并与IMAD在带有缺失值且缺失率为0.3的SMAP和MSL数据的异常检测效果进行对比。此外,由于在Donut和LSTM-AE中没有给出最终确定合适阈值的方式,采用网格搜索得到的F1best分数对各个方法进行比较,最终结果如图6所示。对于存在自动阈值选择策略的方法,则对比阈值确定出的精准率、召回率和F1分数,结果如表2所示。 图6 不同方法异常检测能力上界对比Fig.6 Comparison of anomaly detection of upper boundary performance of different methods 表2 不同异常检测性能对比 由图6可知,在MSL数据集上,缺失率为0.3 时IMAD算法的F1best分数最高,而在SMAP数据集上,带有缺失值的IMAD算法F1best分数为0.840 5, 略低于LSTM-NDT算法的0.887 5,高于其他3种对比算法,说明即使数据具有一定的缺失比例,IMAD算法依然能维持较好的异常检测效果上界。 LSTM-NDT是基于预测的异常检测方法,此类方法具有较大的局限性,一些时序数据由于分布复杂很难预测[28],如MSL中时序数据的分布模式变化较大,因此LSTM-NDT在此数据集上效果较差;在MSL中所有基于重构的方法效果均比此方法更好,因此基于重构的模型相比基于预测的模型在异常检测任务上对不同数据分布的鲁棒性更强,表2也再一次证明了这一点。 此外,由于MSL相比SMAP数据维度和异常种类更多,Donut这类逐个通道进行异常检测的方式在此数据集上F1best分数仅为0.689 4;而IMAD则为0.903 8,这证明了建模多维时序数据通道之间依赖性的有效性;与LSTM-AE方法对比,IMAD算法证明了采用VAE建模随机判断异常值相比重构误差具有更强的鲁棒性;与DAGMM相比,IMAD模型证明了RNN系列模型建模时序数据的有效性。总体而言,与对比方法在全量数据上的异常检测效果上界相比,IMAD采用缺失率为0.3的数据训练测试仍然具有优势,这证明了IMAD算法能在建模缺失值和不规则采样时序数据的同时,保持一个较高的模型表达能力,从而能够有效保证航天器状态的监测。 在实际使用中,无法采用对测试集遍历的方式寻找异常检测效果最优时对应阈值的方法,而图6只是比较了各个模型的表达上界,如何能够自动确定合适阈值逼近上界是地面运维人员关心的问题。从表2可以看出,DAGMM由于无法建模时序依赖关系,且文献[17]中给出的自动阈值确定策略较差,导致其实际性能与IMAD算法通过POT算法自动确定的阈值表现相差较大,而在SMAP数据集上,IMAD算法与LSTM-NDT算法有约5%的差距,但在另一个分布复杂的数据集上,IMAD相比LSTM-NDT能有更好的异常检测效果。 表3给出了IMAD算法采用POT自动阈值选择策略给出算法得到的F1分数与F1best分数对比,可以看出,一旦设置好POT两个重要的参数,模型在不同缺失率下得到的F1分数与模型性能的上界整体差距较小,这证明了基于极值理论自动确定阈值的有效性。 5.3.3 超参数对于模型性能的影响 对于自编码器模型而言,滑窗长度和隐藏层z的维度对于模型性能是十分重要的。为避免RNN建模长序列引起的梯度消失或爆炸问题,引入滑窗输入策略,由于本文数据集采样频率高且局部平稳,此参数对模型性能影响较弱。但对于隐藏层z的维度,若取较大的值,则可能无法获取输入xt有效的低维表示,此时重构异常检测效果会较差;若取较小的值,则可能无法学习到输入变量xt的特征,造成训练的欠拟合,同样会导致异常检测效果较差。因此,模型对于隐藏层z维度的敏感程度会显著地影响模型的鲁棒性。针对缺失率从0.1变化到0.5时的两航空时序数据集,观测隐藏层的维度从1变化到14时的F1best分数的变化,以表示其模型表达能力的上界随z维度的变化,最终结果如图7所示。 从图7可以看出,固定缺失率时,IMAD算法在两个数据集上的F1best分数在一个较小的范围内波动,且能够维持在一个较高的标准上。此外,对比同一个维度不同缺失率下的F1best分数可知,在MSL数据集上,当缺失率为0.3时,总体异常检测性能稍好于其他缺失率的情况;而在SMAP数据集上,则是缺失率为0.4时效果稍好。可能的原因是当缺失率较小时,额外输入的相邻观测值时间间隔矩阵以及缺失值指示矩阵大部分为无用信息,对于模型的表达能力造成了一定的干扰;而缺失率较大时,由于数据缺失较多,模型没有足够的数据有效学习数据的分布,此时效果也会稍差。 图7 隐藏层z维度变化对IMAD性能的影响Fig.7 Influence of hidden z dimension on performance of IMAD 但值得注意的是,图7中两个数据集上即使是最差的F1best分数,仍然要比使用全量数据的对比算法中Donut、LSTM-AE的高,且相比DAGMM及LSTM-NDT在不同数据集上的泛化性能更好一些,这表明不确定性建模对于不同数据分布的鲁棒性,对多维航空时序数据检测是十分重要的。 基于VAE的异常检测模型实际上是通过学习正常数据的分布形态进行异常检测的。图8给出了z的维度取3时,正常数据及异常数据在隐藏空间的分布情况,可以看出,当将包含异常点的滑窗数据给到离线训练模型中时,其编码得到的低维表示(红色点)与正常滑窗数据编码得到的低维表示(蓝色点)在空间中耦合不可分离。这种不可分性表明即使模型输入数据中包含异常点,其低维表示与正常输入数据的低维表示是相近的,因此其对应的重构值仍然是趋于正常的。此时,异常点和与其对应的重构值之间有较大差距,导致其重构概率lgp(x|z)相比正常值对应的重构 图8 输入变量xt的隐层表示Fig.8 Latent representation of input variable xt 概率小,从而能够判别异常点。同时,这也说明VAE模型学习了正常数据的分布,因此,即使xt包含异常值,依然能将其编码至正常数据编码对应的低维流形中去。 航天器状态实时监测是航天任务能够顺利完成的重要保障,而由于航空时序数据具有维度大、时间长、缺失值多、采样不规则等特性,实现实时的线上异常检测较为困难,针对上述非规则采样且带有缺失值的航空遥测多维时序数据异常检测问题,首先提出了IMAD算法,采用GRU-D从模型层面建模多维非规则采样有缺失值数据;然后使用VAE建模不确定性,采用重构概率进行异常检测;最终采用POT算法自动确定合适阈值。在两个真实航空时序数据集上,IMAD均取得了超出当前最新异常检测算法的效果。多个实验表明,IMAD在缺失率、参数、数据集变化时,能够维持较好的异常检测效果,具有较强的鲁棒性。 在本文方法的框架上仍有较多工作可以探究,如通过引入生成对抗网络,采用博弈的思想进一步提高鲁棒性;此外,IMAD中隐层分布假设服从对角高斯分布,与实际情况不符,引入更复杂的分布可能可进一步提高其异常检测的性能。5 实验验证
5.1 数据集介绍及模型评价指标

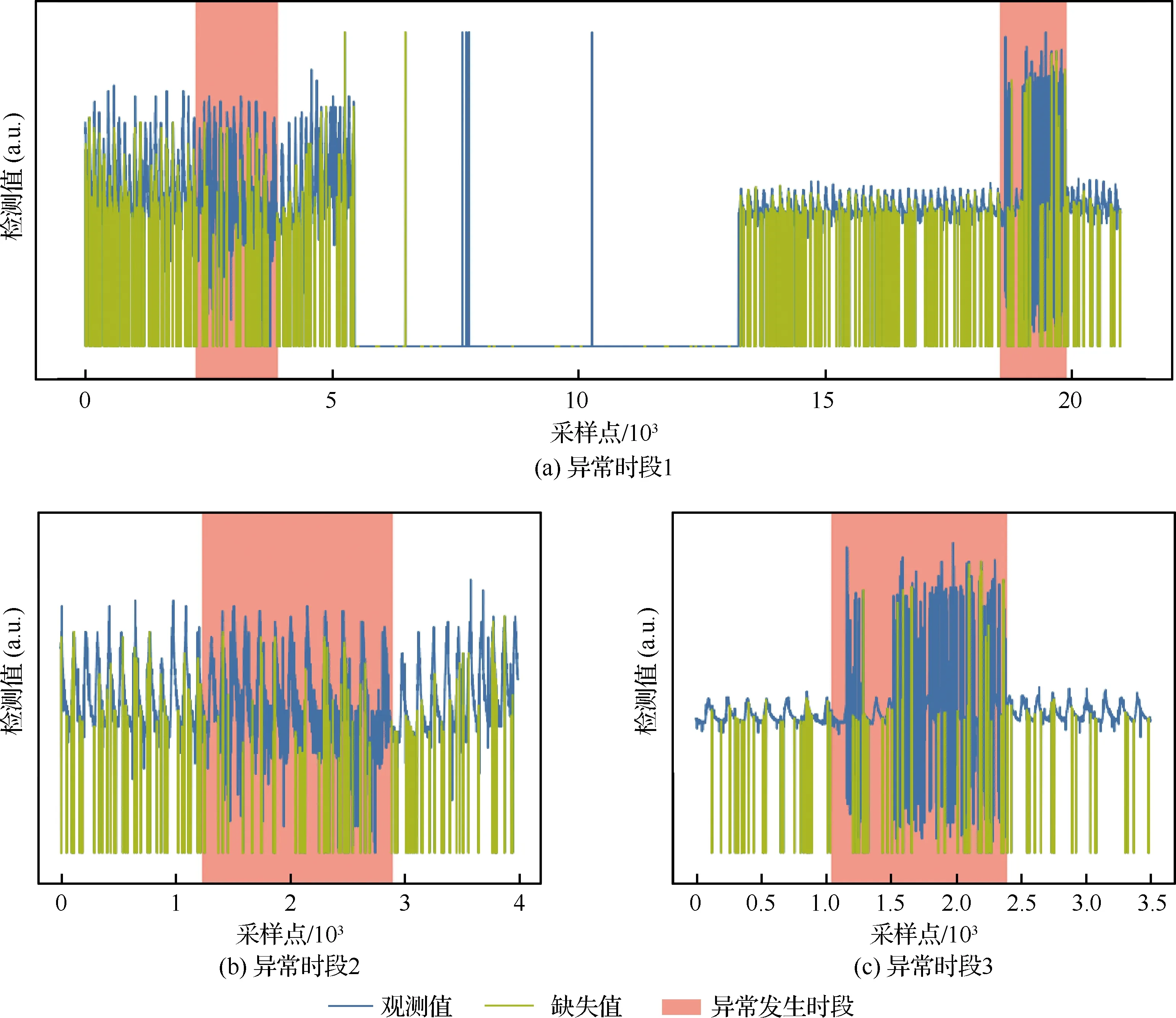
5.2 对比方法及实验参数设置
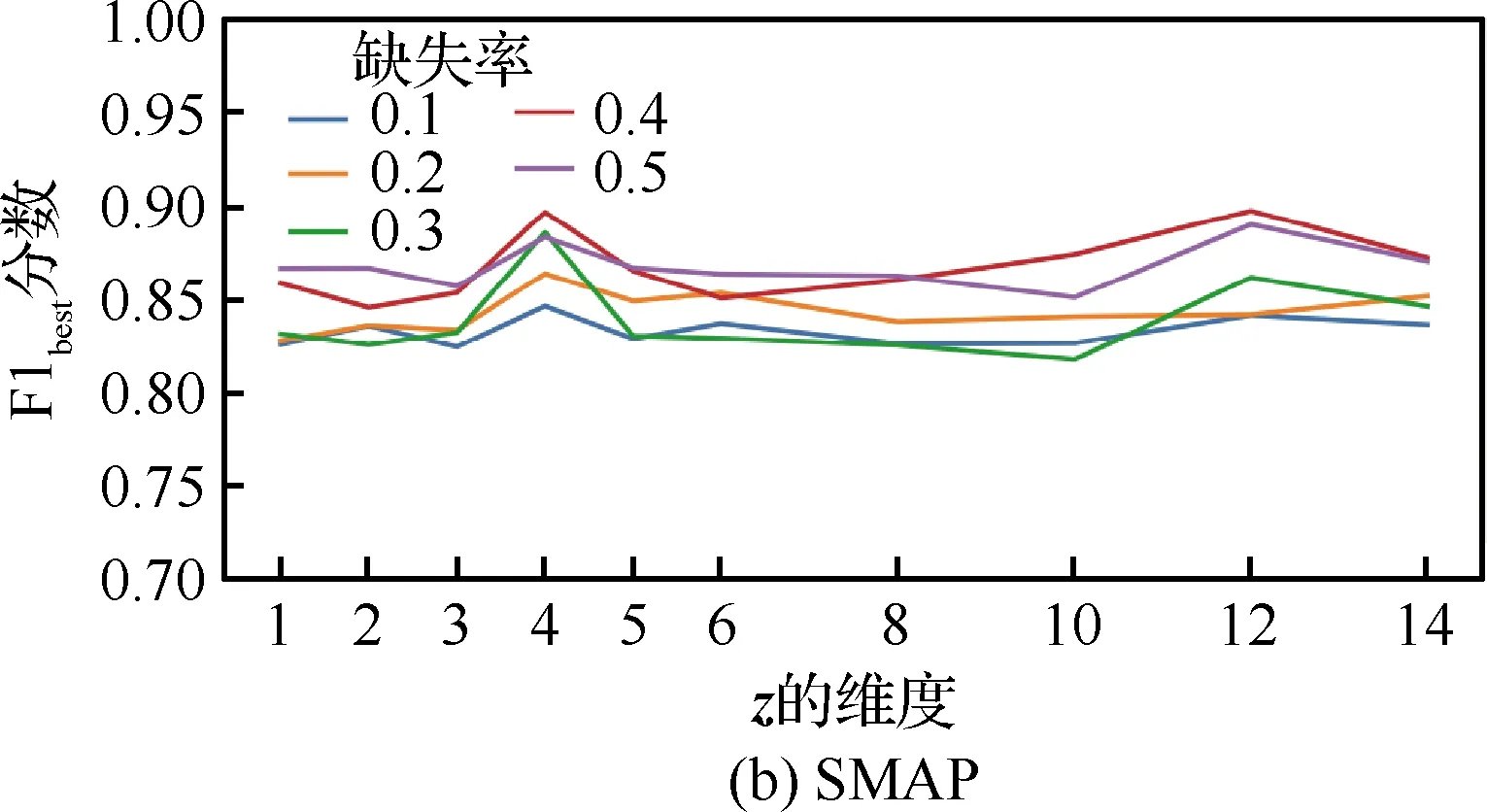
5.3 实验结果及分析





6 结 论

