智能赋能流体力学展望

张伟伟，寇家庆，刘溢浪

西北工业大学 航空学院，西安 710072

流体力学是一门古老的学科，该学科发展最早依赖于数学家和物理学家的贡献，如伯努利、欧拉、纳维、斯托克斯等奠定了基本的流动控制方程。20世纪初，普朗特及其弟子为现代流体力学的发展及应用作出了开创性的贡献。

经典流体力学理论，无论是控制方程还是理论模型，都是基于重要的物理定律，结合一些假设，通过数学推导而形成的。早期的解析方法在处理复杂真实工程问题时，遇到了极大的困难。缩比风洞试验技术和20世纪中叶以来的数值方法为解决实际工程中的流体力学问题起到了有力支撑。特别是20世纪80年代以来，CFD技术的蓬勃发展，极大降低了流体力学分析难度和设计成本。然而，由于湍流、转捩等问题的复杂性，仍有很多基础性和工程应用问题亟待解决。流体力学实验研究近年主要集中在复杂实验系统的开发、先进测试方法和流动显示手段等方面。对于复杂流动机理的分析，更多是对非线性现象的描述性解释，而对其发生机制和各种因素的因果关系理解上还有待深入。对海量、精细化测量数据的信息提取和特征分析为挖掘复杂流动机制提供了新的技术支撑。

人工智能(Artificial Intelligence，AI)[1]是研究、开发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门新的技术科学。人工智能是计算机学科的一个分支，20世纪70年代以来被称为世界三大尖端技术之一(空间技术、能源技术、人工智能)，也被认为是21世纪三大尖端技术(基因工程、纳米科学、人工智能)之一。近30年来，人工智能获得了迅速的发展，在很多学科领域都获得了广泛应用，并取得了丰硕的成果，已逐步成为一个独立的分支，无论在理论和实践上都已自成一个系统。斯坦福大学尼尔逊教授对人工智能下了这样一个定义：“人工智能是关于知识的学科——怎样表示知识以及怎样获得知识并使用知识的科学。”麻省理工学院的温斯顿教授认为：“人工智能就是研究如何使计算机去做过去只有人才能做的智能工作。”这些说法反映了人工智能学科的基本思想和基本内容。总的说来，人工智能研究的一个主要目标是使机器能够胜任一些通常需要人类智能才能完成的复杂工作。但不同的时代、不同的人对这种“复杂工作”的理解是不同的。1997年IBM的深蓝计算机打败当时国际象棋界公认的棋王格里·卡斯帕罗夫，让人们惊叹计算机的力量。2016年Google公司开发的“阿尔法狗”(AlphaGo)战胜了围棋世界冠军，人们惊叹的不是计算机本身，而是人工智能科学的发展。对付人类棋手从来不是“阿尔法狗”的目的，开发公司只是通过围棋来试探它的功力，而研发这一人工智能的最终目的是为了推动社会变革、改变人类命运。人工智能在语言和图像理解、机器翻译、智能控制、自动程序设计、庞大的信息处理/储存与管理等技术层面以及智能交通、医疗健康、教育、安全、金融等与人类生活的方方面面都有着很大的应用前景。2017年7月20日，国务院印发了《新一代人工智能发展规划》，2017年12月，人工智能入选“2017年度中国媒体十大流行语”。

就流体力学研究而言，其途径包括理论分析、数值方法以及实验技术。理论分析和数值方法包括理论解、理论模型、标度理论以及高精度的数值格式、高效计算方法等。目前来看，这些基础性研究成果的发现/提出大多仍是直接依赖于人类的智慧。流体力学通过计算机或在试验中所产生的数据是天生的大数据，如何通过人工智能方法来利用这些大数据，通过机器学习来缓解甚至替代理论/方法层面对人脑的依赖，是一个非常不错的方向。此外，借助人工智能技术，发展流动信息特征提取与融合的智能化也是流体力学发展的迫切需求。另外，发展与流体力学相关的多学科、多物理场耦合模型的智能化更是很多重大型号工程应用的迫切需求。

人工智能作为21世纪又一个新兴学科，流体力学者紧跟时代科技步伐，敏锐捕捉流体力学和人工智能的结合点，开拓新的研究方向，运用新的研究手段解决湍流等一系列经典科学问题。近期，多篇关于流体力学机器学习[2]、数据驱动的湍流建模[3-4]、流动智能控制[5]、人工智能与空气动力学结合[6]、气动优化[7]等的综述及专著[8]发表，在总结流体力学中的人工智能研究方面各有侧重，但对未来的展望偏少，相关研究与航空航天工程问题的结合度较弱。

本文将从智能赋能流体力学的视角，总结和展望流体力学新的研究范式，旨在通过人工智能方法建立或完善流体力学理论、模型和方法，推动流体力学在相关领域应用的智能化，弥补研究者对理论基础和经验的不足。研究内容可以归纳为流体力学方程、模型和方法的智能构建，流动信息特征提取与融合方法的智能化，以及数据驱动的多学科、多物理场耦合建模与控制等，下面将围绕这三个大的方面逐一展开。附录A中给出了人工智能领域一些重要名词的概念，关于人工智能和机器学习基本方法的描述可参阅文献[2, 9]，本文不再赘述。

1 流体力学方程、模型和方法的智能构建

流体力学虽然是一个古老的学科，但至今仍是一个对数学和物理学基础依赖很强的工程科学。没有较好数理基础的工作者，很难得心应手地从事流体力学研究，尤其是在理论和数值方面。即使是流体力学专业研究者，也会觉得方程推导和公式反演枯燥乏味。流体力学学科的发展一直都是依赖于基本方程、基本模型和计算方法。可以说，前人建立的基本理论、模型和方法是流体力学工程应用和进一步理论发展的前提。在大数据时代，通过人工智能方法来构建复杂流体系统的控制方程和基本模型，并发展新型的数值方法提高精度和鲁棒性，减少人工干预和计算成本，是一种新的研究思路，相关研究包括以下几个部分。

1.1 流体力学控制方程的机器学习

流体力学方程的机器学习立足于流动实验和数值手段，获取足够的样本之后，通过特定定解条件下的若干特解，兼顾基本守恒定律和量纲特性，反过来构建流体力学控制方程以及特定环境下简化的运动方程。这一过程和计算流体力学基于给定方程获得数值解的过程恰好相反。

动力学模型是物理系统随时间演化规律的数学描述，对于系统的分析、预测、控制有着重要意义。动力学模型的构建往往需要联系实际的问题，采取适当的假设，利用基本物理原理、守恒定律进行数学或物理推导。现代流体力学虽然已经具备了较完备的理论方程和模型，但仍然有很多复杂问题的理论研究尚不完备，如带化学反应流、多相流、非牛顿流、稀薄流等，这些系统的动力学方程或模型的理论推导难以实现。近年来，机器学习发展迅速，在很多学科领域都获得了广泛应用，并取得了丰硕的成果。机器学习的突出特点是需要大量的数据，从数据中学习系统的物理规律。而流体力学领域的研究常常伴随着大量风洞试验，积累了不同系统、不同初边值条件的大量数据，这使得依靠数据构建系统的控制方程成为了可能。因此，流动控制方程的机器学习成为了解决复杂流体力学问题物理方程匮乏的一个潜在突破口。

20世纪90年代，陆续有学者发展基于数据的机器学习方法，如神经网络、随机森林、支持向量机等，它们具有强大的模型预测能力，在流体领域得到了广泛的应用[10-14]。但这类方法属于“黑箱模型”，缺乏对其运行机理的解释，难以通过模型对系统进行定性分析，另外对于训练区域之外的样本，往往泛化性较低。针对该问题，部分研究者开始着力于发展可解释的流动控制方程的机器学习方法，主要包括符号回归和稀疏回归两类方法。

符号回归方法[15-16]使用遗传编程[17]的思想，首先确定系统所需的终端集合(包括变量s1,s2,s3、随机常数c1,c2,c3等)和函数集合(包括各种运算符+-×÷、数学函数f1,f2,f3等)，然后由终端集合和函数集合随机地产生原始种群(几百个甚至几千个随机方程组成的集合)，而后根据个体适应度对种群进行选择、交叉、变异等操作产生下一代种群(如图1所示[17])，不断循环，直到收敛或者获得足够“优秀”的个体。该方法开创性地实现了工程界寻求已久的目标，即从数据中识别系统的控制方程，并且可以处理复杂的函数形式。然而其不足之处在于计算速度较慢，不能很好地扩展到大型系统，并且容易过拟合[18]。

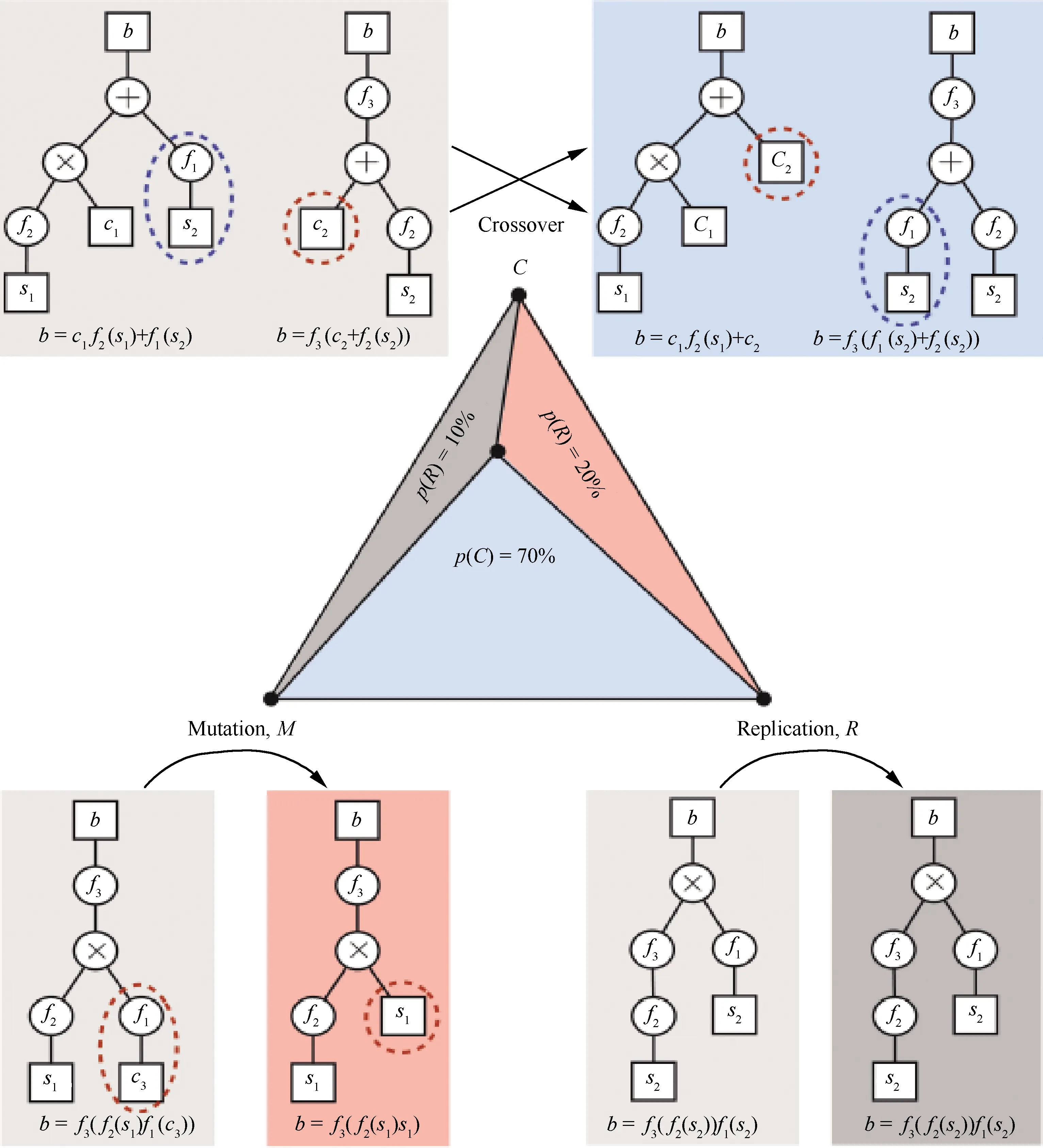
图1 符号回归[17]Fig.1 Symbolic regression[17]

稀疏回归方法首先由Brunton等[18]应用到非线性动力学系统的识别中(Sparse Identification of Nonlinear Dynamics, SINDy)，该方法通过预设一个完备函数库(包含大量可能的函数形式)，将动力学方程表示为完备函数库的线性组合，再利用稀疏回归方法从完备函数库中选择典型的函数，组成简约的微分方程(如图2所示)。他们关于模型方程结构的唯一假设是，系统的动力学行为只由几个重要的控制项决定，也即控制方程在可能的函数空间中是稀疏的，此方法成功地运用到低雷诺数圆柱绕流的低维动力学方程的辨识。之后，SINDy在其他很多流体问题上都得到了应用，比如识别地下水流和污染物传输模型[19]，识别代数雷诺应力模型[20]，识别桥梁的涡致振动系统[21]等。

图2 稀疏非线性动力学辨识方法[18]Fig.2 Sparse identification of nonlinear dynamics method[18]

由于流体力学领域问题的复杂性，系统特征往往需要偏微分方程表征，因此，偏微分方程的识别在流体力学领域尤为重要。Rudy等[22]将SINDy进一步应用于偏微分方程的识别中，提出PDE-FIND方法。该方法通过稀疏回归从包含大量偏微分项的完备函数库中选择最符合数据的偏微分项，简单有效，在许多流体力学方程的识别中均获得了成功。然而，由于数值微分对于噪声数据的不适定，该方法只对高信噪比数据有效。值得注意的是，Schaeffer[23]也独立提出类似的方法。Long 等[24-25]将微分方程的离散过程引入到卷积神经网络中，可以对数据做长时间的持续预测，也可以获得简约的偏微分方程。Chang和Zhang[26]将数据驱动方法和数据同化方法相结合，可以从数据中识别偏微分方程及其附加的模型参数，拓宽了偏微分方程辨识方法的适用范围。对于已知偏微分方程结构的情况，Raissi 等[27-28]引入高斯过程用于辨识方程中的标量系数，该方法可以适用于数据量较少的情况。Raissi 等[29-30]提出了一种物理信息神经网络，可以辨识偏微分方程中的标量参数，该方法通过神经网络对数据进行拟合，并将偏微分方程作为拟合过程中的正则化项，避免了传统数值微分对于噪声数据的不适定问题。Zhang和Ma[31]运用微分方程识别方法，清晰地展示了玻尔兹曼方程和Navier-Stokes(N-S)方程之间的相关性，他们利用分子模拟方法获得流场，而后利用PDE-FIND方法从中识别出了各种流体力学方程。

流体力学方程的机器学习研究面临以下几个难点：

1) 含噪数据的方程辨识问题。对于噪声数据，数值微分误差很大，这为数据驱动的PDE识别方法的应用带来了很大困难。简单地对测量数据进行滤波去噪，或多或少会污染有效信息，并不能够有效解决相关问题。

2) 完备函数库构造原则。现有方法构造完备函数库时，缺乏指导性原则，将各阶导数和各种非线性组合都放进了完备函数库。对于多变量或方程组，通过这种方式构造的完备函数库将过于冗余。需要进一步利用物理量的量纲、方程的物理特征或者基本的守恒律，约束完备函数库的构造过程，剔除掉完备函数库中不必要的项。

3) 微分方程中可能存在的小系数项。如何保证小系数项的精准辨识是个十分棘手的问题，需要发展新的选项准则来保证小系数项在备选项识别过程中不被抛弃。

4) 如何保证推导的方程的守恒性。守恒性是很多物理问题出发的基石，对于数据驱动的微分方程，是否需要以及如何结合基本的物理守恒定律，以保证守恒律，值得未来进一步研究。

1.2 湍流建模的机器学习方法

湍流模型是为了封闭N-S方程中的雷诺应力项而额外补充的方程，主要目的是构建时均流动、空间位置(常用的有壁面距离)与雷诺应力张量或湍流涡黏之间的数学关系式。这一关系式既可以是最早使用的代数式，也可以是微分方程(组)形式。然而，这些经典的湍流模型大多是通过平板、槽道、管道等问题的实验数据，结合基本假设，在一定的理论指导下构建的，模型中有很多经验参数。流体力学应用者将这些模型用到各种复杂工程问题，并通过进一步的实验结果验证相关湍流模型数值结果的精度。现有的雷诺平均湍流模型在分离流中的低适用性和不同模型结果的差异性，给使用者造成极大困惑和不便。随着人工智能时代的到来，数据驱动的机器学习方法在湍流研究领域蓬勃发展，已经成为流体力学研究的热点。这些工作主要包含以下4个方面。

第一，对经典微分方程型湍流模型的改善，称之为数据驱动的灰箱模型。研究者通过高精度数据来减小RANS模型计算的偏差，或者使之能够用于分离流的计算。其研究思路大致有两种，一种是通过改变模型的控制方程形式，如乘以修正系数或给方程增加源项。例如，Tracey等[11]针对二维及三维流动，构建了替代SA模型控制方程中源项的神经网络模型；Zhang和Duraisamy等[12, 32-33]针对修正系数分布或附加源项建立数据驱动模型，改善了原RANS模型的计算精度。张亦知等[34]发展了物理知识约束的湍流模型数据驱动修正方法，并用于槽道湍流的计算模拟。另一种是在RANS模型基础上构造偏差函数，然后将RANS模型和偏差函数的计算结果叠加作为最终的雷诺应力值。例如，Xiao等[35]针对RANS模型计算结果和高分辨率数据之间的雷诺应力偏差进行建模，提高了原有模型的准确性。在采用数据驱动方法的基础上，研究者巧妙地引入了雷诺应力的物理约束，提出了“基于物理的机器学习”概念，所构建的机器学习湍流模型预测周期山算例壁面湍流剪切应力分布结果如图3所示，可以看出预测结果优于RANS结果(Baseline)。

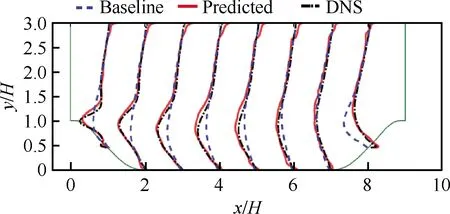
图3 机器学习湍流模型预测周期山算例壁面 湍流剪切应力分布[35]Fig.3 Turbulence modeling based on machine learning to predict wall shear stress distribution for periodic hills[35]

第二，直接构建数据驱动的黑箱模型，以神经网络这种复杂代数模型为主。Ling[14]和Kutz[36]基于Pope推导的基张量和不变量构建了雷诺应力各向异性的张量基神经网络模型(TBNN)。该模型可以刻画二次流中的旋涡结构和波形壁中的分离现象。Zhu等[37]采用RBF神经网络，发展了直接构建纯数据驱动的湍流黑箱代数模型，并成功实现了模型与N-S方程之间的耦合求解。研究结果表明，基于NACA0012翼型的3个亚声速状态算例，所构建的模型可以实现与SA模型相当的精度和更高的计算效率，并对计算状态和几何外形具备很强的泛化能力，打开了人工智能方法解决工程湍流问题的局面，典型计算结果如图4所示。

图4 文献[37]机器学习湍流模型典型结果Fig.4 Representative results for turbulence modeling based on machine learning from Ref. [37]

第三，用数据驱动方法模型化LES中的湍流相关变量。Gamahara和Hattori[38]针对亚格子应力张量的分量分别建立了人工神经网络模型。Maulik等[39]采用人工网络模型预测了时空变化的湍流源项。Wang等[40]用不同机器学习方法和特征研究了亚格子应力封闭。Xie等[41]研究了神经网络结合亚格子模型框架的湍流建模方法及在可压缩湍流模拟中的应用。Zhou等[42]利用神经网络替代亚格子模型，用于LES湍流模拟。这些研究工作仅以高分辨率的数据作为驱动，一定程度上降低了模型封闭或湍流相关变量模型化的难度，证实了纯数据驱动的黑箱模型在湍流研究应用中的可行性。

第四, 将机器学习用于描述和量化传统湍流模型计算结果的不确定度。对于模型参数和模型形式导致的不确定度，可以采用灵敏度分析，概率分析以及贝叶斯方法等加以量化[43-49]。近年来，机器学习方法开始逐渐被应用于模型的不确定度分析。构建RANS模型参数与参数对应的偏差之间的数据驱动模型，通过计算模型的最小值来确定RANS模型的最优参数有利于提高精度[10]。模型研究者可以通过构建分类器来预测流场中RANS模型的不确定区域，进一步地还可以针对模型所确定的不确定区域采用更好的计算方法[50-52]。Singh等[53]结合流场反演和贝叶斯方法来量化RANS模型的不确定度。更多关于RANS模型或LES的不确定度分析可参考文献 [4]。

上述研究工作和湍流建模流程可大致归结为图5所示。图中，湍流模型的构建过程主要包含数据处理、特征选取以及模型框架的确定和参数优化等几个方面。模型框架和参数优化方法的种类繁多，在分类和回归以及各自对应的特定问题中通用性较差，难以界定某种模型或方法的具体优劣性，表1给出了近期相关研究所采用的一些模型。

表1 主要的模型框架及应用Table 1 Main model frameworks and applications

无论采用什么方法，特征选择和数据处理都是未来研究中格外需要重视的方面。单纯地依靠海量数据作为直接输入，通过简单增加神经网络模型的深度和宽度来构建复杂映射关系并不是好的建模策略。要在流动物理机理和模型架构充分理解的基础上对输入数据进行特征提取，特别是结合前人在湍流理论中已经取得的物理规律和经验，如选择不变量，利用各种标度率、量纲分析方法等。在保证精度的情况下，精简输入信息，简化网络模型的维度和复杂性，能够很好地实现模型的精度和泛化能力的平衡。

通过机器学习构建的湍流模型在和N-S方程的耦合过程中存在两种模式，分别称之为单向耦合和双向耦合。单向耦合是先通过RANS基模型与N-S求解器求解出某一个迭代步的初始流场和雷诺应力场或涡黏场，然后运用所构建的湍流模型进行预测，更新湍流生成项，传递给N-S方程，直至迭代收敛，如图6(a)所示。显然，前述的灰箱模型属于这种单向耦合。在有些黑箱模型中仍然需要经典湍流模型提供一些重要的参数作为输入，如文献[14]中需要模型计算的湍动能作为卷积网络的输入，因此也无法实现双向耦合计算，仍是一种单向耦合形式。另一种则与传统RANS模型相同，所构建的模型在从初始流场开始的每一迭代步都与求解器之间互相反馈，将N-S方程迭代输出的空间时均特征给模型作为输入，模型预测的雷诺应力再反馈给N-S方程，直至N-S求解器获得收敛解，如图6(b)所示。

图6 机器学习湍流模型与CFD求解器的耦合Fig.6 Coupling between CFD solver and turbulence model based on machine learning

这种基于神经网络的高维非线性代数型湍流模型有别于经典的微分方程型模型，为新一代湍流模型的构建提供了极大的自由度。一方面可以让使用者根据自己的需求充分发挥自主性，利用特殊应用领域的样本来构建湍流模型，提高湍流模型的针对性，为工程湍流模型的定制化提供了方法基础。另一方面其代数特性还有利于增强鲁棒性和收敛性，提高计算效率。

除了上述已经取得的各种进展之外，对于湍流机器学习这一新兴研究内容，目前仍有许多问题值得注意与研究：

1) 物理先验信息与机器学习模型的融合

湍流的机器学习建模本质上属于物理系统下的机器学习问题，而物理系统一般都存在一些基本的控制方程或者约束，如果可以将这些先验的物理信息融入到机器学习建模过程中，则有望在减少建模数据量的同时提高模型的精确性和泛化性以及模型的可解释性，这将有助于人们对于物理系统的理解。

在使用机器学习方法进行湍流建模时，认为物理信息包含在这些数据中并且假设模型可以从数据中学习到这些信息，这是一种物理先验信息与机器学习模型融合的方法。这种方法可称为是一种隐式的方法，因为物理先验信息主要体现在数据中，没有任何显式的物理规律约束，其结果往往不尽如人意。例如Ling等[57]采用随机森林与神经网络两种方法，系统地比较了是否采用不变量形式作为模型输入的建模效果。其结果表明：将不变量作为输入，显式的加入物理先验信息可以得到更好的结果。

除此之外，也可以将物理先验信息添加到模型损失函数中，在模型的训练过程中以损失的大小体现物理约束。例如，Karpatne 等[58]提出了PGNN(Physics-Guided Neural Network)的概念，将物理的先验信息加入到损失函数的构造中指导网络的学习过程，使得神经网络不仅具备了很高的精确度，预测的结果也符合物理一致性原则，即模型的预测是合乎物理规律的。他们所构造的损失函数形式为

(1)

式中：第1项表征模型预测与真实数据的误差；第2项表征模型的复杂度；第3项表征模型的预测与物理规律的相容程度，包含了物理的先验信息与约束。

2) 模型的泛化性

在湍流机器学习建模研究当中，使用神经网络模型的一个重要考量就是其强大的泛化能力，这使得仅通过对几个特殊流动状态的学习就可以将模型应推广到许多其他状态中，比如仅通过对NACA0012翼型几个流动状态的学习，模型就可以直接推广到若干状态下NACA0014与RAE2822翼型的绕流求解[37]。

但是目前对于模型的泛化性仍处于一个片面的认识阶段，无法确切地给出一个模型的泛化边界，这就大大限制了模型的应用范围，降低了使用人员对于模型的信心。目前对于神经网络的泛化性研究已经有了一些进展[59-60]，但仍然缺乏一个普适的理论。对于模型泛化性能的认识不足将有可能限制机器学习在湍流建模中的应用。

3) 湍流模型与N-S方程耦合求解过程中的稳定性与收敛性

随着机器学习在湍流模型化中的作用越来越明显，模型的输出结果对速度场的影响也越大。一方面，机器学习方法所构建的模型本身可能会输出非物理解，出现局部峰值和光滑性差的输出值，从而降低计算精度。另一方面，模型训练大多是基于某些时刻或流场中某些位置的数据进行的，模型难以包含流场在迭代过程中的全部信息。当模型参与求解器的每一步迭代时，模型的扰动会导致N-S方程求解的流场扰动，继而反馈为模型的输入偏差，形成误差累积。这会造成迭代过程的数值发散，即使对于单向耦合策略甚至非耦合策略，也会造成求解过程的失稳。如果模型的稳定性较差，在非线性很强的大分离流动中，误差累积会导致N-S方程最终计算结果变差。特别是采用高维深度网络，所带来的局部极值对耦合过程的稳定性和收敛性都产生了不利影响。

就目前的经验来看，以下几种措施对于耦合过程中的收敛性与稳定性会起到积极作用：① 对模型的预测值空间光顺之后再与N-S方程耦合迭代；② 对模型输出值进行时间上的光顺平均作为终值与N-S方程耦合迭代；③ 选择合理的模型输入特征；④ 卷积神经网络固有的稀疏特性和空间相关性为提高稳定性和收敛性大有裨益。另外有研究者报告称，将模型输出改写为涡黏格式之后再与N-S方程耦合也可以提高耦合过程的稳定性[61]。

有关湍流建模机器学习详细的综述可进一步参考文献[62]。

1.3 流体物理量纲分析/标度智能化

量纲分析是研究和分析物理问题的有效手段[63-66]，更是流体力学领域最重要的研究方法之一。自然现象和工程问题都可以采用一系列物理量来描述，对于现象和问题的研究目的是要寻求规律，首先把问题所涉及物理量按属性分类，找出不同物理量之间的相互联系及因果关系，通过量纲分析，可以准确地表达各物理量的关系，将多个单变量组合成数目较少的无量纲量，从而简化数学和物理模型[65]。量纲分析法的理论核心是1914年Buckingham提出的“Π定理”[66]：

设某物理问题涉及n个物理量(包括物理常量)P1，P2，…，Pn，而所选取的单位制中有m个基本量(n>m)，则由此可组成n-m个无量纲量Π1，Π2，…，Πn-m。若实际物理问题在物理量P1，P2，…，Pn之间存在物理定律(函数关系)：

f(P1,P2,…，Pn)=0

(2)

则可以表达为相应的无量纲公式:

F(Π1,Π2,…,Πn-m)=0

(3)

标度理论是在总结、分析和归纳实验结果的基础上，提出的一种研究临界现象的唯象理论。当多尺度复杂系统进入一定的稳定状态时，各尺度的动力学自由度之间通常有一种耦合，由于相互作用的自由度数量大，这种耦合往往表现出极大的随机性和无规则性。这时，若物理统计量随尺度的变化呈幂次律，则对这种幂次律的定量刻化就是标度指数，也即：标度律是对多尺度复杂系统临界自组织状态的定量刻划[67]。标度律最早的研究始于前苏联的著名数学家 Kolmogorov[68-70]，他于1941年预言了能谱惯性子区的存在以及著名的-5/3标度律等一系列概念。这些成果也被称为K41理论，是湍流理论发展的一个里程碑。在这之后，标度理论也被广泛应用到其他学科领域。

从量纲分析和标度理论的定义来看，这种方法论从一开始就是依赖于数据的，但是这些方法或准则的建立很大程度上还必须和物理问题的基本内涵分析结合起来，分析越深入，所得的理论越有用。因此说，经典的量纲分析和标度理论需要深厚的理论基础和丰富的研究经验。

基于大量的数值/实验数据，如何利用人工智能技术，发展新的量纲分析方法，实现标度理论的智能化，不仅是流体力学面临的一个空前机遇，而且研究成果可以推广到整个物理学领域。

目前量纲分析与标度理论智能化的研究已有少量发展，相关工作有：

1) Wang等[71]提出了一种量纲函数合成方法。对于已知系统，该方法可以通过传感器获取物理量量纲信息，自动编译合成无量纲组，再通过传感器数据对无量纲组进行拟合。该方法的优势是，对于已知系统实现量纲分析的自动化，所需计算量与计算时间很少，基本可以做到根据传感器数据实时获取系统特征。但该方法只能对已知系统进行分析建模，所采用的无量纲方法也基于传统方法。

2) 多物理场流动问题，如辐照颗粒湍流，涉及复杂的高维参数空间分析。这类问题通过相关的重要无量纲组研究。但传统量纲分析手段存在两个主要缺陷，无量纲组的集合不是唯一的，并且没有量化其相对重要性的通用方法。Jofre等[72]提出了一种数据驱动的方法，通过利用降维领域中的活跃子空间方法来增强Π定理，可以有效地从计算或实验获得的数据中提取重要的无量纲组或标度律。

3) Murari等[73]提出了一种直接从实验信号中提取标度律的方法，并应用于确定托卡马克装置中等离子体L模和H模之间限制阈值的标度律，标度指数可以从神经网络的权值和支持向量机的分离超平面中提取。

上述工作反映了已有研究的3种思路：已知系统量纲分析的自动化，利用机器学习算法识别已知幂次关系的指数项，以及利用机器学习算法从大量参数中识别复杂问题的重要无量纲组。它们都利用机器学习方法代替工程师的工作，提高了已知问题分析的效率和精度。但其共性的问题是，并未利用机器学习算法超越人类的分析识别能力解决科学家/工程师力不能及的问题，在这方面中国科学院力学研究所针对高超声速气动问题进行了一些尝试。

在研制新型高超声速飞行器时，需要进行数以千计次的风洞试验来研究其气动性能。而由于试验设备、成本预算和安全性的限制，要预测的状态点可能位于采样范围之外。这就使得根据已有数据进行外推十分必要。但是，已有的线性拟合、支持向量机和全连接神经网络，在进行外推时预测性能将很快退化。针对上述问题，Luo等[74]提出了一种有监督的自学习方案——自适应空间变换(AST)。AST试图在物理学家的监督下自动检测已知数据的潜在不变关系(标度)。下面简单介绍数据的潜在不变关系和AST方法。

利用风洞试验数据，通过插值、回归、非线性拟合、人工神经网络或支持向量机等方法建立气动力系数J与Ma、Re的近似模型已十分成熟。然而其结果即使在3D空间中，也不容易判断参数如何影响气动力系数(如图7 (a)所示[74])。标度参数可以将多参数问题简化为更简单的问题，并且结果可以在二维空间中可视化(如图7 (b)～图7(d)所示[74])。这使得它更容易解释，使用也更方便，f*就是一种最优标度变换。

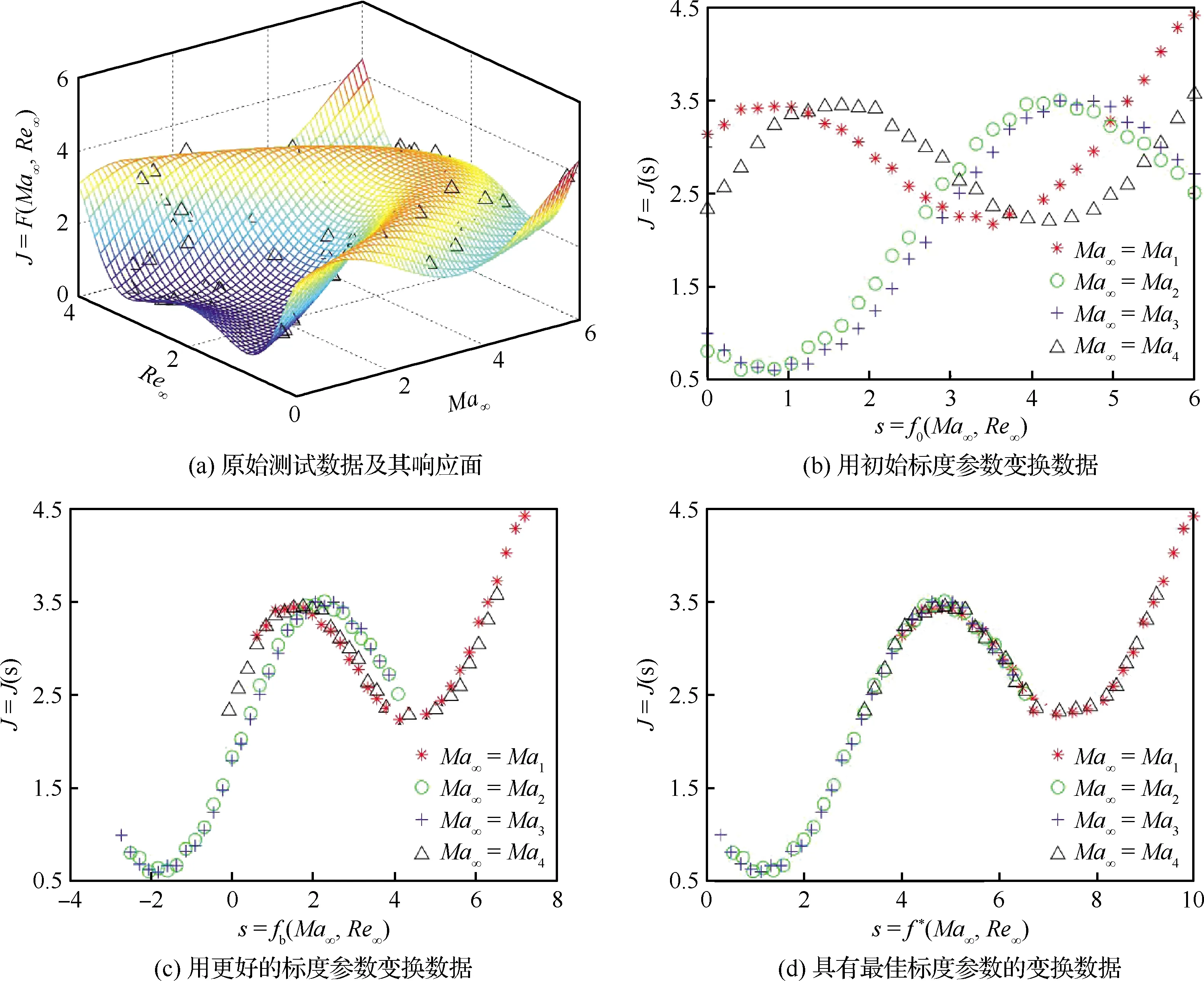
图7 通过自适应空间变换检测关于Ma的不变关系[74]Fig.7 Testing invariance about Ma through adaptive space transformation[74]

继续以上述的简单模型说明AST方法，假设需要检测关于马赫数的不变量，则可以在以下步骤中确定最优标度参数f*。

1) 根据马赫数将原始数据分成：{(Mai,Rei,j,Ji,j)|i=1,2,…，N;j=1,2,…,M}。

2) 在2D空间中构造特征曲线(见图8(a)[74])：J=φi(s)，其中，s=fk(Mai,Rei,j),i=1,2,…,N;j=1,2,…,M。

3) 通过遗传编程实现符号回归方法[75]来优化和更新转换核fk，使得特征曲线趋于彼此重叠(见图8(b)[74])。

图8 AST的初始状态和最终状态[74]Fig.8 Initial and final states of AST[74]

4) 重复步骤2)和3)，直到满足停止准则，并输出最优标度参数f*及其对应的特性曲线。

Luo等[74]利用AST方法识别z=x2+y2解析函数，CFD计算的高超声速10°半角尖锥阻力系数的最优标度参数，并与支持向量机和神经网络方法进行外推预测对比。结果表明，AST在针对较简单且无噪声数据能可靠地外推气动力系数，并且该方法明显优于后两种方法。

上述4项工作已经实现了机器学习算法在量纲分析自动化、标度指数识别、无量纲量提取、最优标度参数识别上的初步应用。公开报道的研究并不多，但量纲分析与标度理论的智能化在复杂问题的研究中将大有可为，后续还可开展的工作与可能面临的挑战有：

1) 实现未知系统的量纲分析智能化。目前已知系统的量纲分析手段已非常成熟，但在面对未知系统时，量纲分析将面临诸多挑战。其一，如何智能判断系统参量是否有缺失。其二，若已判断参量确有缺失，能否自动分析出缺失量的量纲或其他性质。

2) 实现从已有的试验数据中识别最优标度参数，并进行状态外推。现有工作已实现基于特定算例的CFD数据识别最优标度，但基于已有试验数据进行状态外推才是工程界更关心的问题，而这也会面临许多难题。首先，如何判断试验数据的本身是否含有不变关系。其次，如何避免试验数据的噪声对识别精度的影响。最后，复杂问题所涉及的参数量较大，数据的前处理以及相关参数的选择依旧凭借经验。

3) 利用人工智能算法，识别潜在的不变关系。标度律的研究表明，自然界中存在大量符合幂次律的现象。在目前的物理系统中可能存在着很多的潜在不变关系尚未被发现，这种潜在关系甚至可能存在于目前认为不相关的系统之间。

1.4 流动数值模拟方法的智能化

自从计算流体力学诞生以来，人们一直从事着推进算法实现和应用的便捷化、自动化工作，以便于计算流体力学在工程中的推广。如在网格剖分方面，从最早期的结构化网格，发展到非结构网格、笛卡尔网格以及各种混合网格和无网格方法，以期提高网格生成的自动化。各种网格变形方法，如自适应网格、嵌套网格等，也是流动数值模拟智能化的体现。在流场显示方法，Tecplot等软件已经极大程度降低流体力学研究者对流场后置处理的劳动强度。

对于流动数值模拟方面，基于人工智能的求解方法也开始崭露头角。传统的流场数值模拟方法是基于流动的控制方程，将流场求解域进行空间离散化，运用时空数值格式，把连续的偏微分形式的方程转化为离散点上的代数方程进行求解。相对于传统的流场数值模拟方法，人工智能数值求解方法是基于数据或物理模型驱动的，不需要对偏微分方程进行复杂的时空离散化，在计算精度和计算效率方面有潜在的优势，其计算精度和数据来源可信度、网络架构以及网络泛化能力等相关。目前，这种研究主要分为两大类，一类是有样本数据驱动的监督学习神经网络方法，另一类是无样本物理驱动的自学习神经网络方法。

基于样本数据的神经网络方法首先根据现有的流场模拟方法或实验手段获得高可信度流场样本数据，采用机器学习方法对样本数据进行学习，构建神经网络映射关系代替原始的偏微分方程，能够快速、高效获得流场数值解。Sekar等[76]提出一种快速预测翼型流场的深度神经网络方法，通过卷积神经网络(CNN)对翼型进行参数化，构建以翼型参数、雷诺数、攻角等为输入，流场分布为输出的深度神经网络映射模型，通过学习大量的训练样本，无需数值迭代，模型就能够快速预测出翼型流场分布，效率很高，在二维定常层流流场中取得了很好的效果。这种方法采用卷积神经网络将大量的翼型样本(1 550个，UIUC数据库)作为图像进行学习，提取描述翼型的16个参数作为流场预测模型的输入，以达到对外形泛化的目的。图9和图10给出了该方法对翼型流场分布的预测结果以及翼型表面压力系数Cp分布的预测结果和力/力矩系数随迎角变化的结果，并与原始CFD样本数据的对比。这种方法的优势是一旦模型训练好以后，无需进行复杂的流场求解，直接通过神经网络就可以给出流场的空间分布结果，计算效率很高，而且对不同翼型有泛化能力。然而，以卷积网络学习图象的方式对大量翼型进行参数化表达并不能够准确、精细地反映翼型的微小变化对流场的扰动，尤其是在近壁附面层区域；而且在MLP网络的构建过程中，该模型并没有着重考虑对翼型阻力特性有重要影响的近壁区建模精度，因此，目前该方法仅能用于雷诺数较小(千的量级)的层流流场建模，对于高雷诺数湍流场的建模还有一定的问题；此外，从图10也可以看出，这种模型对于升力和力矩系数的预测精度很高，但对于阻力系数的预测精度不足，表明这种方法对于翼型摩阻分布的预测精度还不够准确。

图9 NACA63415翼型流场压力分布和速度分布结果与CFD样本数据结果对比(Re=1 900, α=7°)[76]Fig.9 Comparison of pressure and velocity distribution between model and CFD data for NACA64315 airfoil (Re=1 900, α=7°)[76]

图10 NACA63415翼型(Re=1 900, α=7°)表面压力系数分布和两种翼型的集中力预测结果[76]Fig.10 Results of NACA63415 airfoil (Re=1 900, α=7°)for surface pressure coefficient distribution, and prediction of aerodynamic coefficients of two airfoils[76]

Fukami等[77]采用CNN网络将低分辨率的流场作为图像进行学习，能够重构出高分辨率的湍流场，同样不需要求解控制方程，直接通过神经网络学习即可对流场进行高分辨率重构，在层流圆柱绕流和各向同性湍流中验证了方法的有效性。目前该方法网络输入的低分辨率流场是从DNS方法获得的高分辨率流场图象池化而来的，并不是低精度计算方法得到的真实流场，仅验证了CNN网络有能力对高分辨率湍流场进行重构还原。Raissi等[78-80]引入物理嵌入的神经网络(Physical Informed Neural Network, PINN)求解偏微分方程，通过特定流场的若干观测值对神经网络进行训练，以控制方程作为约束，并不需要引入边界条件就可实现对特定区域的流场预测。在损失函数的构造中同时引入样本数据以及偏微分方程本身的偏差量，在网络训练过程中通过数值微分的方法计算方程中的偏导数项，进而采用神经网络重构整个流场分布，研究以层流圆柱绕流为例，成功实现了对卡门涡街与涡致振动的预测。采用PINN求解N-S方程的架构，如图11[79]所示，输入变量是流场物理域的时变空间坐标x、y和时间t，输出是流场解变量，速度、压力等。图12[78]是采用PINN方法求解圆柱绕流问题得到的压力场分布与真实流场结果的对比，预测结果能够准确还原样本流场。这种方法最大的特点是将控制方程引入到网络训练的损失函数，作为额外的约束项，能够使得训练网络的偏导数也满足控制方程，得到的结果更符合物理规律，其本质是以控制方程为约束条件的拉格朗日乘子法求解最小值问题，只是采用自动微分方法求解了神经网络对于输入变量的偏导数。而且，可以通过选取流场中某一个变量的样本进行训练，就能够反演所有流场变量的分布，能够有效解决测量数据缺失情况下的全流场变量的重构。另一方面，这种方法并没有考虑边界条件的影响，为了准确反演流场，必须在近壁区取足够多的样本数据进行训练，这对于高雷诺数湍流问题会造成样本数据量巨大，网络难以训练的问题。此外，这种流场求解方法仅能用于流场的重构，并没有泛化能力，即对于不同的来流状态或者边界条件，需要重新训练PINN网络，可以看做是一种数据同化方法。基于PINN方法，Jagtap等[81]发展了守恒PINN(Conservative PINN)方法，首先将流场划分为多个不同的子区域，在每个子区域中采用PINN方法进行单独求解，提高了原方法对于复杂边界流场问题求解的适用性。此外，PINN 方法也被推广用于包含激波间断的高速流场的数值模拟[82]。>

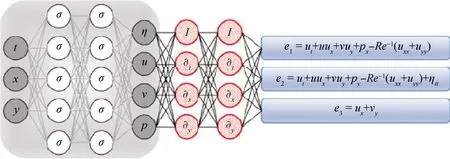
图11 PINN求解N-S方程的网络架构[79]Fig.11 Network structure of PINN to solve N-S equation[79]

图12 PINN方法求解圆柱绕流问题得到的压力场分布与CFD计算结果的对比[78]Fig.12 Comparison of pressure flow fields of flow past cylinder between PINN and CFD solver[78]

样本数据驱动的神经网络方法需要大量的高可信度样本数据，然而当样本数据较少或无法获得流场样本数据时，这类方法就难以适用。因此，有学者通过引入边界条件约束，提出无样本物理驱动的神经网络方法。这类方法不需要带标签的流场样本数据，直接将物理方程和边界条件融入神经网络的损失函数中，是一种有别于传统CFD方法的数值模拟新方法。Zhu[83]和Geneva[84]等采用卷积编码——解码神经网络模型对偏微分方程进行了数值求解，将流场以图像数据的形式作为初始解输入给卷积网络，可以用少量的卷积核表示高维流场数据，大大降低的流场求解维度，再把控制方程和边界条件均融合到网络的损失函数中，不需要任何训练样本数据，通过模型方程驱动神经网络映射方程的数值解，称之为物理约束的代理模型(Physics-Constrained Surrogate, PCS)，数值结果优于数据驱动的网络模型。Karumuri等[85]同样基于无样本数据方法，采用深度全连接残差网络求解了二维椭圆型随机偏微分方程。Sun等[86]将这种方法推广到求解参数化的Navier-Stokes方程中，采用深度神经网络对真实的血管流动进行了模拟。Wei等[87]提出了一种基于深度强化学习技术的流场求解方法(Deep Reinforcement Learning solver，DRL solver)，将控制方程、边界条件和初始条件均引入到网络的损失函数中，实现了从离散求解域的初始随机分布场收敛到稳定的最终解，这种方法的基本框架如图13所示。DRL solver被用于求解Van der Pol方程、Lorenz方程、Burgers 方程以及Schrödinger方程等几种典型偏微分方程的数值解，图14是该方法求解一维Burgers 方程得到的瞬时流场分布结果，可以看出DRL solver能够准确捕捉激波间断，且没有激波附近的数值振荡。目前该方法仅能用于求解简单、低维的稳定收敛问题，不能求解多极值发散问题，并且求解精度受制于迭代的时间步长，存在像传统数值方法的稳定性和收敛性问题，不能求解复杂的湍流场问题。

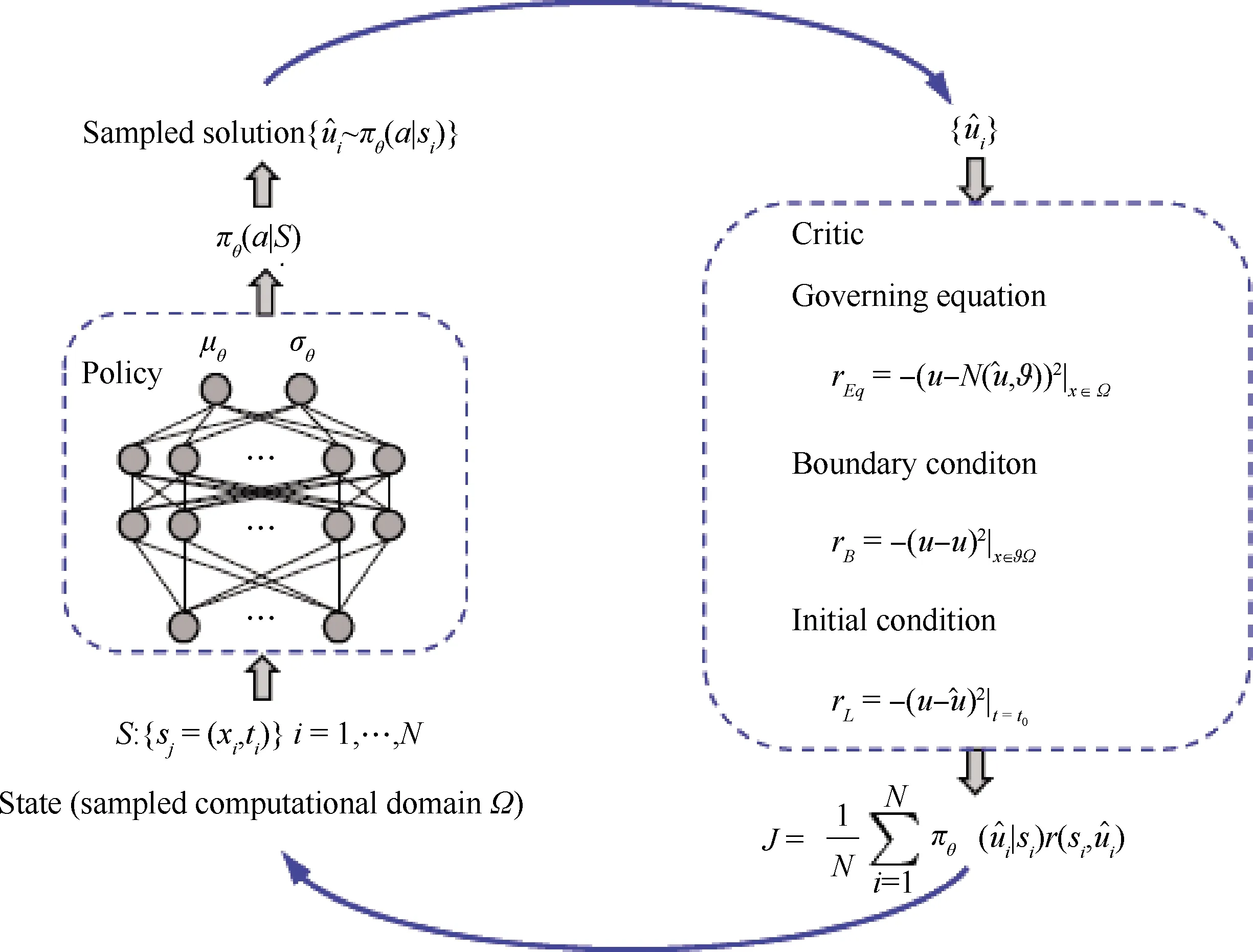
图13 DRL solver的求解框架[87]Fig.13 Solution framework for DRL solver[87]

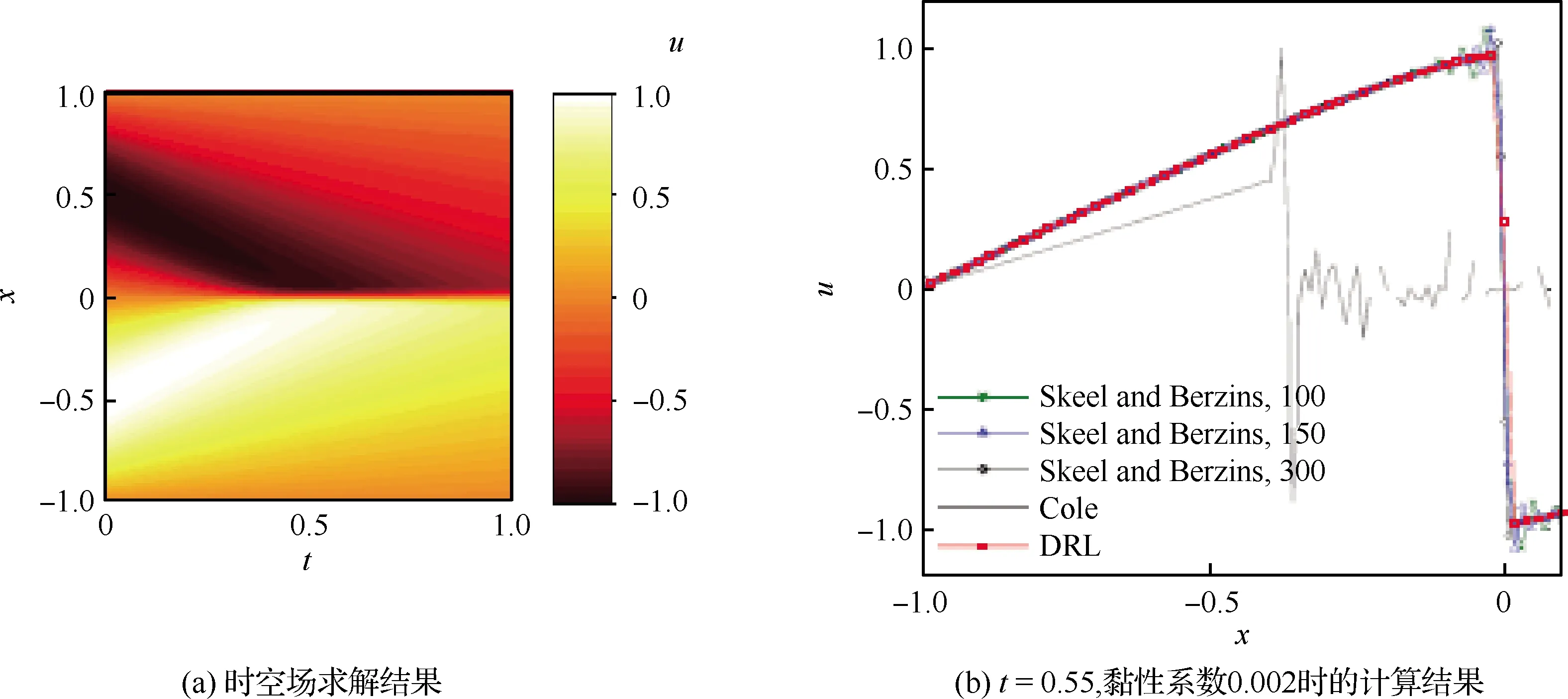
图14 DRL solver求解Burgers方程得到的数值解[87]Fig.14 Numerical solution from DLR solver for Burgers equation[87]

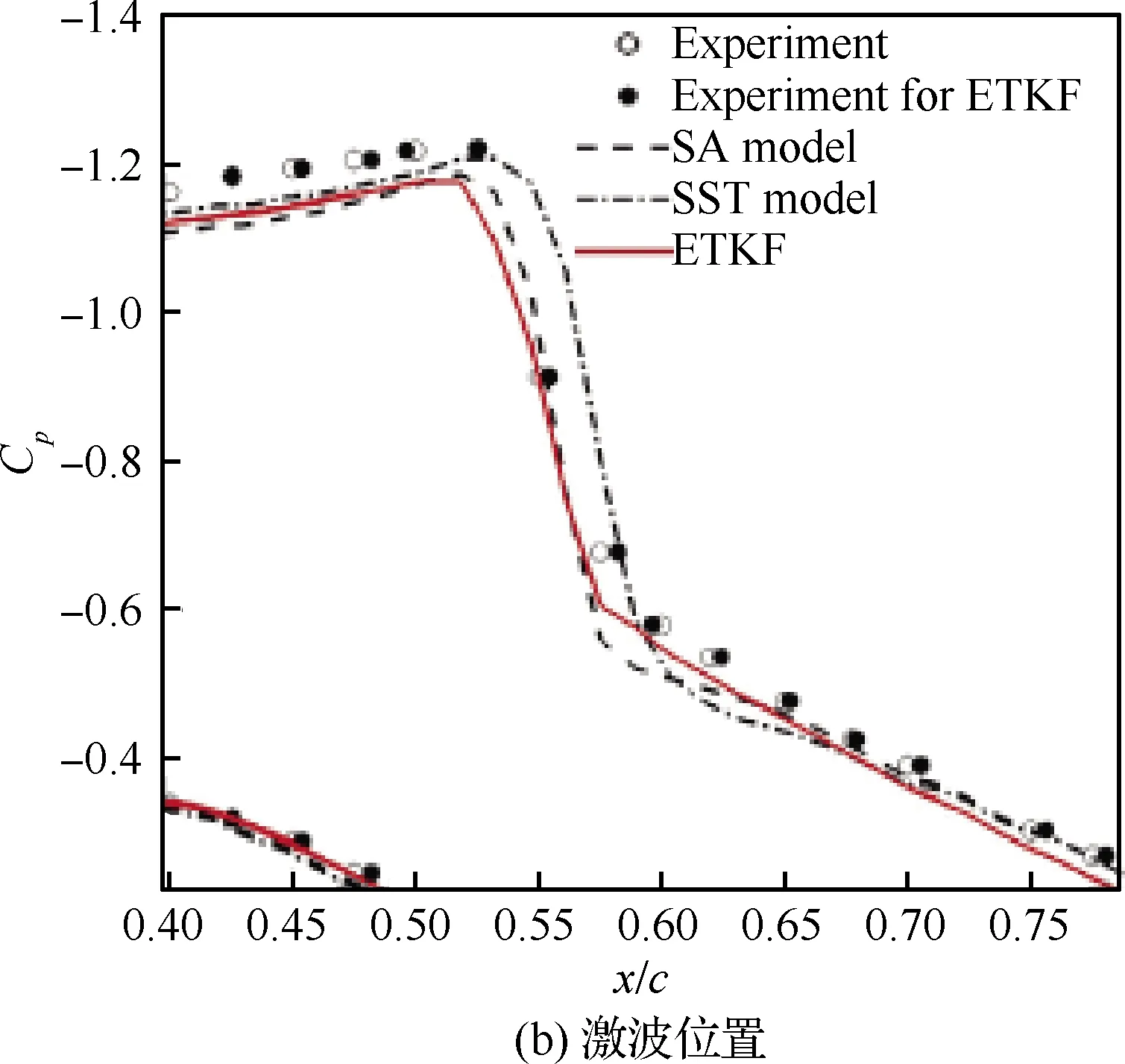
上述基于人工智能的流场求解方法对于高雷诺数、高维湍流问题均存在很大困难，因为这类方法需要基于大量精细的高可信度流场样本数据或面临极高维的网络训练优化问题，由于现有的实验测量手段无法获得精细的湍流流场信息，尤其是边界层内的湍流速度、压力以及摩擦阻力等关键物理参数，数据样本仅能通过高可信度的数值模拟方法(DNS/LES)获得，而对于高雷诺湍流场，高可信度样本数据获取代价巨大。基于上述问题，结合实验数据和数值模拟的数据同化方法被用于高可信度湍流样本的获取以及传统湍流模型的修正。其基本思想是，以实验测得的流场分布数据作为高可信度参考点，通过低精度数值模拟方法计算湍流场分布，采用数据同化方法对低精度模型进行修正，使得计算结果与实验观测数据相差最小。Foures等[88]采用DNS方法获得平均流场稀疏数据，将RANS方程中的雷诺应力项视作外力项，通过基于变分法则和Lagrange乘子法的数据同化技术确定外力项，使得RANS结果能够最好地符合DNS样本数据。Symon等[89-90]基于Foures的工作将数据同化方法拓展用于更高雷诺数的平均流场重构，以实验获得的实测速度场作为观测值，并通过Resolvent 分析方法选择了合理的实验观测点位置。Kato等[91]采用基于ETKT(Ensemble Transform Kalman Filter)技术的数据同化方法对风洞试验状态的来流攻角和马赫数进行了不确定性评估，并给出了修正后的实验初始条件和数值模拟的湍流涡黏场，采用修正后的参数重新求解流场，能够获得和试验数据更加吻合的结果。图15给出了数据同化方法计算RAE2822翼型跨声速流动压力分布的结果，可以看出，相对于传统湍流模型，数据同化方法计算得到的压力分布结果与试验值更为符合。

图15 数据同化方法得到的RAE2822翼型压力 系数分布结果[91]Fig.15 Pressure coefficient distribution of RAE2822 airfoil based on data assimilation[91]

另一方面，基于传统经典的偏微分方程形式的湍流封闭模式框架，根据高可信度实验数据，数据同化方法也被众多学者用于修正湍流模型方程中的经验参数，以提高湍流模拟的数值精度。Kato和OBayashi[92]应用集成Kalman Filter 基于平板湍流样本数据标定SA湍流模型中的参数。Li等[93]发展了数据驱动自适应RANSk-ω模型，通过自适应调整k-ω模型中的自由参数，将自适应法则与CFD求解器耦合，改善原始k-ω模型的精度。Deng等[94]采用集成卡尔曼滤波方法，通过实验测得的速度场数据，分别对SA模型、k-ε模型和k-ω模型中的经验参数进行标定，确定和实验测量速度吻合最好的模型参数。另外，数据同化方法也被用于非定常流场的重构[95]以及LES湍流模拟[96-97]。

此外，基于机器学习技术的智能化方法还被用于流场重构[98-99]、流动显示[100-101]、流场特征提取[102-103]、激波探测[104-105]和限制器构造[106-107]等方面。可以说，人工智能方法用于流动数值模拟方面的研究方兴未艾，值得流体力学研究者积极探索。

针对流动模拟数值方法智能化，还有以下几个问题需要进一步开展深入研究：

1) 智能化流场求解方法的收敛性和稳定性

智能化流场求解方法同样面临收敛性和稳定性问题，尤其是对于复杂高雷诺数湍流问题的求解，湍流高维、强非线性、非定常的特性会给机器学习带来极大的难度，样本数据的复杂性一方面必然要求网络架构更大、更深，才能够更好地模拟极高自由度问题；另一方面网络架构的复杂性会造成流场求解过程中收敛性和稳定性的恶化。如何平衡两者之间的矛盾，提高收敛性和稳定性是智能化流场求解方法的关键问题。

2) 数据同化的降维方法

数据同化方法应用于模型参数的修正，维度很低，容易实现，但当数据同化方法用于流场同化时，会面临极高维的优化问题，因为以所有的流场变量为自由度，优化每个网格的流场参数代价极大。因此对于场数据的同化问题，如何进行数据精简、特征提取等技术发展有效的降维方法，尤其是对于高雷诺数湍流场的同化问题，是这方面研究的一个难点。

3) 智能化流场求解方法的泛化性

流场数值解和初始条件、边界条件密切相关，机器学习方法所构建的模型是从数据到数据的映射，模型的泛化性很大程度上取决于样本数据的范围，而样本数据仅仅是某些特定流动状态和特定边界下的流场特解，并不适用于任意初边值条件下的流动。因此，机器学习模型如何考虑初始条件和边界条件的影响，是提升智能化流场求解方法泛化性的关键。

2 流动特征提取与数据融合方法的智能化

本节涉及流动大数据的人工智能处理。流体力学无论是通过数值仿真还是通过风洞试验，所产生的数据信息都是海量的。如何从海量的信息中提取关键特征；如何将不同的气动数据来源进行智能融合，提高数据的精准度等，很多都与智能化算法和模型紧密相关。下面就流动特征提取与数据挖掘、多源气动数据的智能融合单独展开。

2.1 流动特征提取与数据挖掘

流体力学无论是基于数值模拟还是数字化的实验手段，是一个产生海量数据的典型学科。海量流动信息传输和读取都成为一个耗时的工作，研究者如何从中提取重要信息特征成为了一个重要的课题。

为准确分析复杂流体的动力学特征，从海量的流动数据中提取主要信息更容易理解流动行为，进而建立数据驱动的流动演化模型。海量流场信息的数据挖掘模型可用于气动优化、流动控制、多场耦合以及加速收敛等问题。流动控制需要基于准确的模型，可通过数据驱动方法发展有效的流体动力学模型，基于该模型进行控制律设计[108]。多场耦合问题中，通过挖掘海量流动信息，可以大大加速流体模块的仿真，从而提高多物理场分析效率[109]。在流场求解过程中，引入数据挖掘方法，还可大幅加速流场的收敛[110-112]。

流场数据挖掘手段包括线性模态分析和非线性特征提取两大类。线性模态分析是流场数据挖掘的主要渠道。通过模态分析可以得到高维流动系统的特征子空间/特征结构，从而将高维流场分解成少量主要成分的线性叠加。这些子空间为原始高维流动提供了新的坐标变换，在新的坐标系内，流动特征具有更低维的表达方式，更便于理解流动的非线性动力学行为。针对特征提取方法本身存在的一些挑战，例如变参数、时变动力学建模，目前也开展了初步的探索。当前广泛采用的流体力学特征提取手段主要包含本征正交分解(POD)[113]和动力学模态分解(DMD)[114-116]两种模态分解方法。POD和DMD是基于两种典型的分析角度出发的，即能量和频率。POD从能量角度出发，保证数据在POD子空间中投影的残差在L2范数意义上最小。实际操作中这种分解是基于奇异值分解(SVD)方法，并根据奇异值大小对模态重要性进行排序。然而POD本身只是提供了一种数据分析的方法，还需要对获得的模态系数进行二次分析，建立动力学的模型。另外，POD方法本身仅仅从能量角度出发，可能会忽略一些能量上不占优但同样对动力学过程有较大影响的流动成分。

基于POD的建模可通过嵌入式和非嵌入式两种方式实现。嵌入式模型即在建立POD系数演化模型时需要将模态通过Galerkin投影映射到流动控制方程(线化或完全非线性的N-S方程)上[117-119]。由于这种方法往往需要修改源代码，并且需要提前知道控制方程，因此被称为嵌入式方法。将控制方程投影到模态坐标系后，可以获得低维的模态系数关于时间的常微分方程或者简单的代数方程，并通过时间推进或非线性迭代方法求解。由于N-S方程的非线性的对流过程，该POD-Galerkin系统为带二次项的非线性方程。方程本身能反映非定常流动的主要特征，结合能量分析可以进一步研究流动的能量传递和能量平衡特点。尽管嵌入式方法直接利用流动的控制方程，但是由于在降阶过程中引入了模态截断，被截断的成分无法体现在模型中，往往导致系统不稳定[120]。为解决这一问题，需要采取额外的模型封闭手段。对于非嵌入式方法，直接基于系统辨识，从模态系数演化和流动状态量中提取动力学特征[121-123]。这种方法的优势在于不需要知道控制方程，是一种完全数据驱动的建模过程。但是非嵌入式建模本质上是一种黑箱学习，其精度和泛化能力主要依赖模型训练样本，以及选择的辨识算法。各种常用的的非线性系统辨识算法均可用于模型辨识，且对于不同的问题各有所长。这其中一种特殊的方法是基于POD-Galerkin模型架构本身的回归方法，即在确定非线性模型为多项式形式后进行参数辨识[18]。如果对集中力进行预测，例如气动弹性中关心位移和力的映射关系，这种方法和基于输入输出的直接非线性系统辨识方法相比没有明显优势。

不同于POD，DMD则是从频率角度，从非定常流场数据中直接得到具有单一频率的流动模态和控制方程的数据驱动方法。DMD方法的本质是基于线性系统理论，将高维流动演化看做线性动力学过程，通过辨识流场演化的高维线性动力学算子，得到表征流场信息的低阶模态(特征向量)及其对应的Ritz特征值。DMD 方法的最大特点是这些流动模态具有单一频率和增长率，在分析动力学线性和周期性流动中有很大优势。另外，因为DMD可以通过各个模态特征值表征流动演化过程，因此不需要额外建立控制方程。这种同时得到模态特征和动力学信息的特点，使DMD方法相比于目前基于系统辨识(利用时间序列和输入输出样本)和特征提取(利用空间样本)的流场降阶而言，具有时空耦合建模的独特优势。由于DMD的方法的简洁直观，及其能够从频率角度加深对流动的理解，目前在流体力学问题中已得到广泛应用。针对标准DMD方法在实际中存在的诸多挑战，也发展了很多不同的改进算法，例如优化改进精度[124-126]、改进模态选择[127-128]、增加外输入项[129-131]等。介于POD的能量最优和DMD的频率最优之间也发展了RDMD[132]和SPOD[133]方法，从而在频率和能量条件之间进行平衡。特别需要指出，Kou和Zhang[128]提出了针对DMD模态选择的能量指标，能够优先提取出重要的模态，同时过滤掉快速衰减的伪模态；针对外输入系统，Kou和Zhang[131]发展了一种两步辨识的DMDX方法，对于近失稳流动具有很高的建模精度。DMD方法目前已被用于分析不同的复杂流动现象，如跨声速抖振[134-135]、大攻角飞行器流动[136]、压气机叶栅分离流动[137]、高超声速边界层转捩[138]等。DMD方法的详细介绍可参考文献[139]。

通过聚类分析和流形学习方法，可以挖掘流场快照数据之间的内在联系，从而进行特征提取。流形学习观点认为，实际中的高维数据往往是通过一个低维流形映射到高维空间上的，因此只要得到低维流形就可以对该高维数据进行表示。需要指出POD本身也是一种线性的流形学习方法。而非线性流形学习方法可以对流动数据进行非线性的信息挖掘。这种方法的本质是基于某种流场快照之间相似度的度量指标，把某个特定的流动通过与已知的样本状态相关联，从而用已知状态表示新的流动状态。根据度量指标的不同，可以有不同的分析方法。目前已得到应用的典型方法包括聚类分析[144]、核POD(Kernel POD)[145]、等距映射(Isomap)[146]、局部线性嵌入[147]。聚类分析是一种对样本进行分类的方法，而这种方法结合其他手段也可对动力学过程的相似性进行分析，并用于控制系统设计。这种方法本身存在一些固定参数，这些参数对结果有较大影响，因此需要一些经验进行选择。

数据驱动的非线性特征提取可以通过神经网络直接学习，即构建一个自编码器实现流动快照的自映射。这种方法的降维是通过神经网络隐含层中仅采用少量神经元而实现的。这种思路最早由Milano和Koumoutsakos用于近壁面湍流的建模中[148]。近年来随着深度学习的发展，基于深度神经网络的特征提取和降维方法再次得到关注并开始用于流体力学问题[149]。Huang等[150]利用深度神经网络构建了数据驱动的火焰演化过程预测模型，通过二维流场得到了三维结构。惠心雨等[151]通过深度神经网络，发展了周期性流动的预测方法。叶舒然等[152]研究了自编码器方法在流场降阶中的应用。蔡声泽等[153-154]通过神经网络研究了PIV数据中的粒子运动预测方法。

当前流动特征提取的研究主要存在3个主要的技术难点。首先是建立变参数的动力学模型。当前特征提取模型对于单一系统参数下，已经能够取得较好的精度。然而对于变参数状态和非样本状态，模型的泛化能力仍然值得进一步研究，例如对于不同马赫数、迎角下的非定常流动进行建模。对于变参数模型，需要确保在一定参数范围内均具有较好的性能，因此需要在一定参数范围内进行采样。除了常用的拉丁超立方采样外，基于贪婪算法的采样方法在此类模型中应用广泛。对于基于模态的模型，目前有3种手段实现变参数动力学建模：对模态进行内插、采用局部基函数和分离变量法。模态内插方法是对不同参数之间的基函数进行插值，得到目标参数下的基函数。这种插值典型方法是基于Grossman流形[155]或样条插值[156]。此外也可以对降维后的系统方程直接进行插值。局部基函数法是将不同参数下的快照根据一定准则进行分类，在各个类内建立局部基函数，并在预测过程中根据当前类别，引入对应类的局部基降维[157]。这两种方法精度的关键是插值方法，但是目前并没有具体理论给出如何对其进行选择。分离变量法是求解偏微分方程的常用方法，对于建立数据驱动的低维模型同样有所启发。针对参数化系统的典型降阶方法，例如减基法[158]和本征广义分解[159]，就是基于这种思路。这种方法将偏微分方程的解按照空间基、时间基和参数基进行分离，从而将系统参数变化隐含在与参数相关、但是时空解耦的独立系数中。这种方法因为建模过程中需要求解非线性问题，具体实现过程较为繁琐。

其次是模态自适应。模态自适应主要指根据具体研究的问题、目的以及动力学系统的变化，对基函数进行调整。由于特征提取本身是服务于优化、控制等问题，研究者对于某个特定的输出量更为关心。因此一个较为直接的方法是将建模问题转化为优化问题，基于特定的目标函数对于基函数进行优化，如集中力[160]和模态稀疏性[161]等。这种面向目标的模型优化问题对于确定研究目标的建模上具有较好效果。针对模型控制问题，也可以结合控制模型对于可控性和可观性的要求，得到满足控制目的的最优基函数，典型方法如平衡POD[162-163]。这种面向目标的模型调整由于涉及到优化过程，在训练过程中可能需要较大的计算量。模态自适应的另一方面指在系统仿真过程中，在线更新模态以适应系统变化。例如针对瞬态流动问题，时间相关的基函数更能捕捉流场从不稳定平衡点到完全饱和状态的发展过程[164]。对于系统仿真的在线过程，随着实时的快照增加和系统参数变化，模型的基函数可以根据一些高效的算法逐步更新。例如在线的DMD方法[165]或者在线的SVD[166]。针对这种时间相关的问题，需要平衡计算效率和模型精度。

最后是基于流场测量进行特征提取。基于流场测量的特征提取方法指根据流场中少量观测点，对整体流动进行重构或建模。通常这种方法是在流场全局特征基函数已知的情况下，从流场局部点的测量结果中得到整个流场的信息。用于补全流场中缺失信息的Gappy POD方法是其中一种典型方法[167-168]。这种方法本质上将模态系数的求取问题简化为在若干点上的最小二乘求解，不仅降低了计算量，也降低了POD方法本身对全局快照的依赖。在此基础上发展的错点估计[169]、经验插值[170]和离散经验插值[171]，进一步对POD-Galerkin模型通过低维点建模和非线性项估计提供了计算工具。近年来，研究者采用压缩感知方法取代最小二乘方法，从少量观测点的测量结果中选择重要的基函数，建立动力学模型[172]。此外，这种方法本身也为流场估计时的传感器选择提供指导，即通过优化流场测量点位置，以确定流动重构或状态估计最精确的测量位置，用于流动控制中传感器的配置[173]。这种方法的一个约束条件是必须提前已知全局的流动模态，这些模态通常是固定的，而且流场预测精度跟选择的观测点关系很大。

在流动信息数据挖掘方面，未来的研究依然是从建模方法和应用两个角度出发。对于建模方法本身，可以考虑在频率和能量之外找到另一个切入点以描述复杂流动问题；结合 N-S方程和湍流物理，可以发展出更有效的特征提取方法；线性模态分析方法处理强间断流场的问题仍有待克服；此外，对于模型实际应用中的各种需求，如前文提到的模型自适应、在线更新、状态估计等，可以发展出效率和精度更高的方法。从应用的角度，可以考虑更加复杂的变参数操作环境，提出新的建模方法；或者从数据特征提取模型本身的泛化能力，尤其是变参数、非样本点、变几何外形等情况出发，发展改进上述性能的特征提取方法；此外，不同于当前对标准模型如圆柱、方腔、射流等的特征提取，对于更复杂的流动现象进行特征提取也是未来要关注的重要问题。

2.2 多源气动力数据的智能融合

在当前的航空航天工程领域，针对目标飞行器气动数据的获取途径主要包括数值计算、风洞试验与飞行试验三大手段。然而在实际应用中，不同手段获得的气动数据不仅结果常常存在差异性，而且误差来源和数据特性也不尽相同。例如，数值仿真方法有着实施简单、方便灵活等特点，却因为物理模型(特别是湍流模型)的不明确，复杂流动的模拟往往与真实结果存在较大出入；风洞试验的数据精度高，但存在洞壁干扰、支架干扰、雷诺数、气动弹性、真实气体效应等影响，不能完全模拟真实飞行情况[174]；而飞行试验产生的数据是客观的，但数据量通常偏少，且由于发动机推力的不明确，来流条件存在扰动，传感器精度等问题也会导致辨识的数据存在偏差。虽然获取准确可靠的气动力数据可以通过建造更先进的风洞、采用更高性能的数值模拟系统以及进行更多更精细的飞行试验，但在短时间内采用单一方式提高气动力数据精准度的程度有限，不能完全满足新一代飞行器研制的需要，而且将付出高昂的成本[174]。研究者希望可以将这些复杂来源的气动力数据进行综合利用，一方面降低气动数据获取成本，最大限度的提升气动力数据库的整体精度。另一方面，设计所长期积累的大量历史气动数据在新型号的设计过程中并没有得到有效利用，使得设计过程中不得不开展重复性的气动计算或实验工作。数据融合技术恰好呼应了结合了这一工程背景的需求，作为代表的多源气动力高效高精度建模方法得到了广泛关注。现有的研究至少包括面向不同精度来源的数据融合、不同手段的数据融合、不同对象的数据融合以及缺失流动信息的弥补等相关工作。有关计算、风洞和飞行数据的融合，在流体力学领域有一个经典的研究方向——天地一致性研究，本质目标也是完成相关差异性分析和多源数据的融合。

数据融合技术是指将多种来源的数据和信息相结合，以便更好地改进、估计和利用数据[175]。其本质上是通过对多种测量手段的数据进行充分利用和合理支配，利用数据估计、建模、采集管理等手段，将这些测量结果在时间或空间上的冗余或互补信息依据某种准则来进行综合，产生与被测对象更准确的信息、更一致的解释或描述，获得具有最大可信度的最优结果[174]。数据融合的特点在于可以针对不同来源的数据进行信息互补，获取空间或时间的全面信息。基于不确定度分析、数据估计等手段，可以获得具有最大可信度的一致性结果。数据融合与1.4节中数据同化的差异，体现在数据同化通常是先已知部分测量结果，然后在数值求解过程中对模型或方程源项进行动态调整，使得最终数值解趋同于测量值，从而提高数值模拟的准度。而数据融合是对多种来源已经产生的数据进行事后归一，提高数据的一致性和利用效率。

对于气动力多源数据融合方法的研究，目前主要围绕以下两类问题展开：

第一，气动力数据源之间存在明显精度差异的数据融合问题(有相对真解的数据融合问题)。因为计算成本、变量多样、鲁棒性等条件限制，高精度的气动数据(比如飞行试验等)难以充分获得，而针对低精度气动数据的获取比较便利，考虑到低精度气动数据与高精度气动数据的匹配特性，低精度和高精度模型具有相近的或者有关联的内在特征，两种模型之间的差异可能是一个简单的函数关系，只需要少量高精度样本即可准确建立[176]。因此可以通过混合高精度与低精度数据(或模型)建立数据融合模型以逼近更高的数据精度[177-180]。

第二，气动数据精度区分不明确，状态不匹配的数据融合问题。采用数值计算气动数据、风洞试验数据与飞行试验数据对飞行器气动力或模型进行确定时，需要考虑不同状态、不同数据来源的影响。不同气动数据间的状态与参数很难达到统一，这时就需要针对不同状态、不同来源的数据进行融合，提升多源气动力数据库的一致性和精度[174, 179, 181]。

2.2.1 针对高、低精度数据的气动力融合方法

在实际工程中往往认为，相较于仿真结果试验数据的精度较为准确。在这种思路下，形成了不同精度的气动数据源，一般认为，飞行试验测量所得到气动数据是准确的，而很大程度上，风洞试验数据与数值计算结果都是这一气动数据的近似。由于飞行试验成本高、周期长，难以直接获得覆盖所有飞行状态的气动力数据，即高精度气动数据量不足以满足设计需求。与此同时低精度气动数据获取较为灵活，可以为高维的飞行状态数据建模提供参考，但是又面临精度的缺陷。为了调节上述矛盾，研究者提出了利用数据融合技术将低精度数据或模型和高精度数据融合在一起建模的思想，即变精度模型的概念，也有文献称为变可信度、变复杂度模型。

在这一基础上，研究发展了基于不确定度的加权平均方法[174, 178]、相关性分析方法、基于Kriging形式的变精度模型[182-184]等传统数据融合方法。这些方法形式简便，利用代数公式的形式将低精度数据与高精度模型联系起来，通过合理分配加权权值大小获得不同精度数据的融合结果。但是，基于代数形式的融合模型往往很难满足高维以及非线性的设计需求，在数据一致性较差的点还会导致误差被进一步放大，如图16[178，184]所示。

图16 基于Kriging模型的CFD-风洞试验 气动力数据融合方法Fig.16 Data fusion method based on Kriging model and CFD-wind tunnel test aerodynamic data

随着以神经网络为代表的人工智能方法的引入，高斯回归[179]、径向基函数神经网络[180]、卷积神经网络、残差神经网络等新的模型开始被应用于数据融合研究。利用神经网络的自学习自适应能力，可以很好地挖掘高、低精度数据间的非线性联系，避免传统修正方法导致的特定区间的误差放大。而且通过模型的训练验证过程，可以有效提高数据融合的全局精度，避免传统方法中的局部过拟合现象。借助这些方法，Belyaev等[179]实现了针对全局非均匀气动数据的高斯回归融合方法，将大量试验与计算气动数据进行融合，并对比了全局与局部精度下的融合结果，如图17所示。相比于传统加权方法，高斯回归有着更高的全局精度和泛化特性，更适用于覆盖全飞行包线的非线性数据融合问题。针对非定常数据融合问题的研究目前开展的较少，Kou和Zhang[185]首先采用多核神经网络模型，将变精度模型推广到非定常气动力模型中，实现了利用低精度欧拉结果对于N-S方程数值结果的逼近，如图18所示。随着机动飞行高精度模拟和控制律设计的需要，多源非定常气动数据的融合将是一个非常值得关注的研究方向。

图17 不同数据融合准则对全局融合精度的对比[179]Fig.17 Comparison of accuracy based on data fusion with different criteria[179]

2.2.2 针对不同状态数据的气动力融合方法

在数据融合的研究中，针对不同状态、不同传感器下的观测结果的数据融合始终是一个关注重点。随着深度学习等大数据研究方法的推广，与数据融合相结合的相关工作已经很好地应用于图像处理与障碍物检测方向[186-187]。Jin等[188]通过卷积神经网络，利用圆柱表面压力测量预测了全局速度场。Ye等[189]通过卷积神经网络建立了从速度场到压强分布的预测。在实验流体力学中，温新等[190]利用数据融合方法，基于高维空间最邻近法则，实现了基于全局与局部的流场PIV结果下的高分辨率的流场重构，如图19所示。

在风洞试验数据与飞行试验气动数据的融合过程中，为了提升数据关联性，提出了一种基于无量纲关联参数的关联方法，利用风洞试验相似律中的参数组合，降低风洞试验与飞行试验气动数据差异[191]，一定程度上可以实现不同状态的数据融合。通过关联参数可以保留气动数据的主要特征，提升气动数据在高维空间中的线性一致性。由于这种方法受到飞行器外形与参数区间的限制[191]，目前还处于比较初步的研究阶段。

利用随机森林[192]等机器学习方法进行关联特征提取[193-194]也是目前比较重要的一个研究方向。在这一基础上，可以考虑将气动准则中的物理无量纲关联参数作为待选的识别项引入，利用随机森林等数据挖掘方法，进而建立不同物理状态与时空数据下的多源气动数据的数据融合准则，提升多源气动数据一致性。

总而言之，多源气动力数据的融合具有重要工程价值与研究意义，利用不同数据源的特征进行相互关联，提升气动数据一致性，降低气动数据获取代价，可以有效提升飞行器设计与试验效率，大幅降低设计周期。智能化方法的引入，很好地契合了气动大数据特征，可以有效利用历史气动数据和智能化方法，对融合方法改进和完善，有效挖掘气动数据的内在联系，降低多源数据的内部偏差。多源气动数据智能融合将对以下的研究领域带来崭新的思路和意想不到的收获。

针对动态失速的气动性能预测方法，普遍基于经验、半经验模型，很多参数单纯从试验现象出发，难以从广泛的数据中获得普遍、一致的结论。随着机器学习方法的引入，越来越多的经验、半经验模型开始被更复杂、更精确的黑箱、半黑箱模型取代，在动态失速等复杂气动性能预测方面发挥出重要作用。在数据融合的背景下，基于机器学习算法，通过耦合低精度模型或者低精度控制方程，进行数据融合的复杂运动下气动力预测成为重要的研究方向。

飞行器数字孪生在智能制造和运行维护中发挥越来越重要的作用。在飞行器设计环节，能否提供高精度的空气动力参数是决定数字孪生模型可信度的核心。多源气动数据融合将在降低气动数据获取成本、提高精度及一致性方面发挥重要的作用，特别是在飞行器复杂动力学特性与飞行包线确认方面，将有效解决性能评估和控制律设计长期依赖试飞环节的困境，可极大降低设计风险、缩短型号研制周期。

针对多源气动数据融合的智能化方法研究方面，依然面临着广泛而又深入的挑战。

1) 在融合架构、准则和算法上需要进一步的深入，尤其是需要将智能融合方法和流体力学基本的误差理论进行有机结合，来实现不同手段、状态等条件下的多源复杂数据间的信息融合。

2) 流体力学产生的大数据与其对应的高维流动状态而言，本质上是一个小样本问题，在飞行试验中表现的尤为典型。飞行试验产生的小样本数据如何与风洞/计算数据进行有效融合，将是一个长期的挑战性研究工作。

3) 针对历史型号积累的气动数据如何和新型号设计过程进行融合的研究还不多，其难点在于融合模型不仅涉及流动状态的维度，而且需要包括主要几何特征的维度，极大地扩展了融合模型的空间，针对有限的数据，小样本问题将更加突出。

4) 融合模型不仅包括数据和数据的融合，还可以体现为经典的气动模型和数据的融合，这种融合模型将能有效提升模型的可解释性和可信任性。

3 数据驱动的多学科、多物理场耦合建模与控制

本节涉及流体力学智能化的应用方向，很多流体力学智能化的初期工作实质上是在这些应用领域的需求牵引下起步的。初步归纳起来，至少包括以下3个方面。

3.1 数据驱动的多场耦合建模

在航空航天、风工程、海洋和能源等领域，流体力学常常与其他学科耦合，构成多物理场耦合问题，比如以颤振、嗡鸣为代表的流固耦合问题和高超声速下的流-固-热耦合问题。多场耦合问题威胁着飞行安全，具有复杂性和普遍性，亟待深入研究。随着计算机性能的提升和计算力学的发展，出现了针对多物理场非线性系统的多场耦合仿真。然而直接耦合模拟不仅计算量巨大，并且有时建立在对某些复杂子学科很难准确计算的基础上(如气动热、气动噪声等问题)，可信度缺乏保障。另一方面，笼统、海量的多场耦合大数据很难直接为工程师提供清晰、准确的设计思路，尤其是在设计初期的方案选择阶段，无法为工程设计提供有力的技术支撑。

随着人工智能时代的到来，数据驱动的模型化工作取得了较大进展。这些工作为多场耦合仿真提供了“化整为零”的新思路，并且有针对性地提高了相关学科的计算效率或精度，这是传统计算方法(如工程方法和数值模拟)所不能兼顾的。在此基础上，再进行“化零为整”的耦合架构设计，这种思路不仅提升了分析效率，而且极大提升了多学科、多场耦合复杂问题的可分析性和可设计性。目前，已开展的与流体相关的多场耦合智能化工作可归纳为以下几个方面：

第一，非定常气动力建模，如表2所示。非定常气动力建模是气动弹性力学研究的重要内容和关键技术。经典模型诸如基于线化势流理论的Wagner模型、Theodorsen模型等，数据驱动的气动力模型通常基于模态坐标，获取强迫运动的模态位移-广义气动力数据，利用系统辨识方法训练一个能够描述从运动状态到广义非定常气动力的动态模型，如Volterra级数[195]和ARMA模型[196]。为了模拟大振幅运动下气动力的非线性非定常特性，发展了BP神经网络[197]、RBF回归神经网络[198]、分层模型[199]、混合模型[200]、支持向量机[201]等方法。为了提高非线性模型在不同流动或外形参数下的泛化能力，提出了变马赫数模型，如递归神经网络[202]、多核神经网络[203]、模糊神经网络[204]、长短时记忆网络(LSTM)[205-206]等。为了适应模态振型的变化，提出了适用于任意振型的气动力模型[207]。所发展的降阶模型，特别是动态线性模型十分便于复杂流固耦合动力学机理的研究，如跨声速抖振锁频机理与控制率的设计[208-209]。可见，非定常气动力建模不仅是流体力学的工作，同时也很大程度上推动了气动弹性力学的发展。

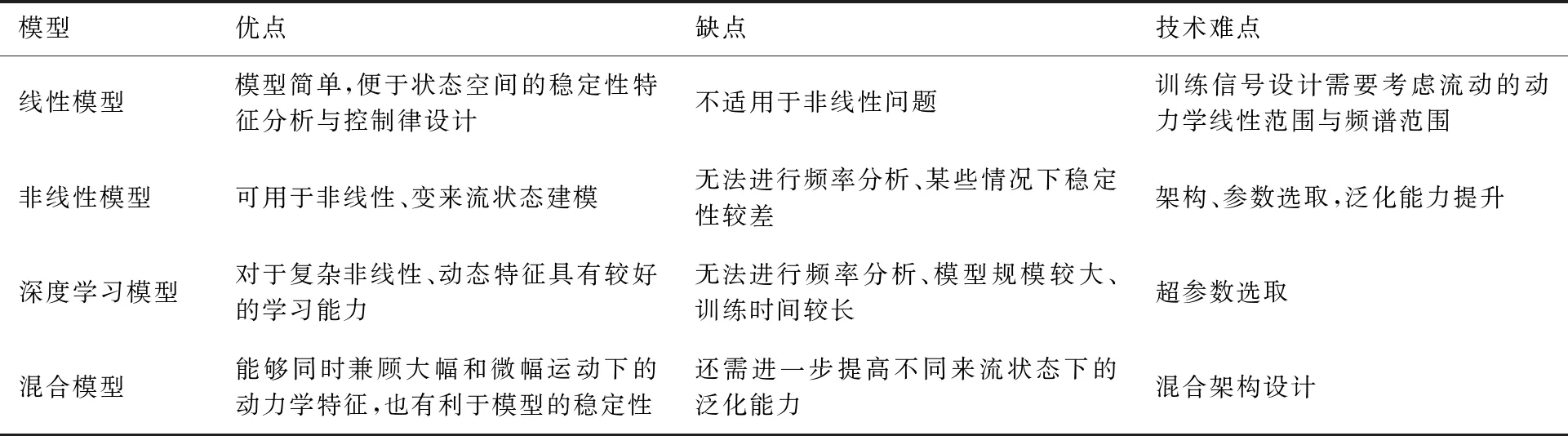
表2 非定常气动力建模方法总结Table 2 Summary of unsteady aerodynamic modeling methods

第二，表面气动热建模，如表3所示。气动热模型的输入为表面温度场及来流参数，输出为表面热流场。气动热建模有两种思路：全局建模方法和当地建模方法。全局建模方法试图建立从“场”到“场”的映射关系，如在文献[210]中，表面温度场采用一组多项式基线性表示，热流场采用POD基表示。为了获取热流场的POD基，需要事先设定代表性工况并在其中进行抽样，对每个样本进行定常CFD的气动热分析，获取所有样本的热流场作为POD分析的输入。最后，用Kriging模型建立输入和输出之间的映射关系。在热气动弹性双向耦合中，气动热还受物面变形场影响，这时气动热模型的输入还需要包含降阶后的表面变形，这增加了气动热建模的输入维度和建模成本。全局性建模方法的不足在于需要大量的基向量，且基向量的选取准则需要进行特殊设计，普适性不足。由于高超声速热流场分布具有较强的“当地性”[211]，即某个位置的气动热只与当地的壁面条件和边界层外缘条件相关，因此可采用当地建模方法，建立从“点”到“点”的气动热模型。比如，Lenoard计算X-43舵面热流时，先假定一系列均布的壁面温度，通过SHABP软件得到不同壁面温度下的一系列热流分布，再建立从当地温度、来流参数到当地热流的插值模型[212]，但文献[213]指出表面温度梯度也会影响到热流场分布。

表3 气动热建模方法总结Table 3 Summary of aerothermal modeling methods

第三，对非线性结构的建模。传统的模态坐标下的结构运动方程仅适用于线性结构。为了高效分析几何非线性结构，研究者发展了一种基于结构模态的带有非线性刚度项的结构动力学降阶模型[214]。首先，需要选择一组基，使得结构的位移响应可以用这组基线性表示。之后，将全阶动力学方程通过Galerkin投影映射到基空间，从而实现降阶。降阶后的具有非线性刚度的结构动力学方程(仅第i阶模态)为

(4)

基于上述子学科模型，可开展耦合架构研究。以热气动弹性问题为例，提出的耦合架构包括单向耦合和双向耦合，如图20所示。单向耦合仅考虑气动热对结构带来的影响，而不考虑结构变形对气动热带来的反作用。然而有研究表明：如果不考虑变形对气动热的反作用，将会过高估计结构在高超声速流中的耐久度，从而造成潜在的危险[218]，因此在大变形壁板颤振时域分析等情况中，有必要使用双向耦合架构。

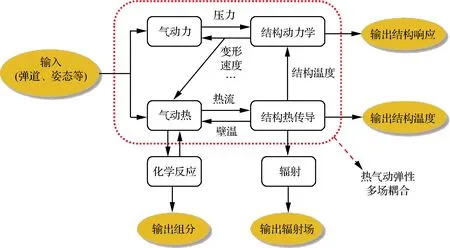
图20 热气动弹性双向耦合架构Fig.20 Two-way coupling framework for aerothermoelastic analysis

在子学科建模工作中，较为成熟的是非定常气动力的建模，已基本完成了集中力(包括刚体的集中力/力矩和弹性体的广义力)的静、动态建模。

但在多场耦合分析模型化中，仍有不少工作需要进一步深入，具体如下：

1) 分布载荷和物理场的降阶方法

气动弹性力学的降阶分析中，通过结构模态可将分布气动载荷的建模转化为模态气动力的建模，实际上不必涉及分布信息的建模。而在气动热建模过程中，分布的热载荷建模就显得必不可少。目前，大部分分布信息建模都通过设计一系列“基函数”来实现线性降维。在未来的多场耦合建模中，“基”的设计依然是重点研究的方向。在人工智能领域还诞生了以“自编码器”为代表的非线性降阶方法，该方法有望应用于那些不易寻找基函数的系统或线性降阶方法无效的情况(如间断场)。然而，自编码器在应用中也会面临网络规模较大、超参数选取困难等技术性问题。另外，分布信息的降维，除了面临时间维度和流动状态的变化维度，若考虑外形的调整，还将面临几何维度引入这一挑战。变外形、变状态下的非定常流场降阶是具有挑战性的研究领域。

2) 动态、非线性、时变/变参系统的模型化

在物理场降阶的基础上，可进一步建立从“场”到“场”的数据驱动模型，除了气动力建模，待开展的建模工作还有：气动热-结构热传导系统的建模、从结构温度场到模态频率、振型的映射模型等。以上这些建模面临的动态特性或者非线性关系可沿用非线性气动力建模的思路解决。此外，在多场耦合中，由于其他物理场会随时间演化，所建立的模型必须考虑整个系统的时变性。比如在高超声速流-固-热耦合中，结构受热使得结构模态实时变化，因此在建立气动力模型时，必须考虑结构模态的时变性。对此，可沿用适用于任意振型的气动力建模方法对高超声速非定常气动力进行模型化研究。

3) 复杂多场/多学科问题耦合特征的定量评估与简化策略可行性研究

在多场耦合问题中，有些因素是必须要耦合考虑的，而有些因素可以解耦考虑，不仅可以减少成本，而且降低了分析的难度。但目前，耦合系统的简化还主要依赖研究者的感觉和经验，比如流-固-热耦合中的单向和双向耦合策略。如何对耦合程度进行定量评估和分析是下一步值得研究的方向。

4) 在模型化的基础上，开展多场耦合问题的机理研究

基于气动力建模开展的复杂流固耦合机理研究已经取得了丰富的成果。在更多物理场耦合建模的基础上，可以进一步开展多场耦合的机理研究，如流固热耦合、流固声耦合等，实现拨开云雾见天日，透过数据看本质。

3.2 气动外形智能优化设计

气动外形设计是流体力学领域最先迈入智能化的方向。传统的气动外形设计在一定的理论基础上结合经验，再通过风洞试验验证，但革命性的突破更多依赖于流体力学理论和思想的进步，如普朗特厚翼型的提出，不仅没有增加阻力，还提升了最大升力系数改善了失速特性；薄翼型/后掠思想的提出支撑了音障的突破；后来还有层流翼型、超临界翼型等新概念和思想。经过几十年的发展，气动外形设计从理论指导下依赖于风洞试验与设计人员经验的试凑法逐步发展成为CFD与数值优化方法相融合的气动外形优化方法。包含气动特性数值评估、飞行器外形参数化技术、空间网格重构技术等，为气动设计带来了突破性的进展。气动外形优化技术能够减小对设计者经验的依赖，显著提高飞行器设计性能，并大幅提升气动设计的自动化水平。人工智能与气动设计的融合主要体现在优化方法上，因为篇幅所限，不再具体展开，另一方面体现在数据驱动的模型辅助优化设计。

模型辅助的气动优化设计研究主要从模型援助的优化方法(Surrogate Aided Optimization, SAO)与基于代理模型的优化算法(Surrogate-Based Optimization, SBO) 两个方向展开。SAO方法的主要思路是根据进化算法的每一代种群信息建立近似的局部代理模型，进而对种群中的个体进行评估及排序。这样便有助于快速剔除不需要的种群个体，从而能够大幅提高遗传算法(Genetic)、粒子群算法(PSO)、进化差分算法(DE)等全局算法的寻优效率。通过模型不精确预估的形式帮助进化算法寻找最优解[219-224]。SBO方法通过抽样方法建立在设计空间内与CFD等效的近似代理模型，然后通过全局优化算法调用该近似的代理模型进行气动外形优化设计。SBO 方法包含3个主要要素：① 近似代理模型；② 抽样方法；③ 优化算法。目前，各种各样的代理模型应用于气动形状优化，例如，Kriging模型[225-229]、神经网络[230-231]、多项式响应面[232]、支持向量机[233]、本征正交分解[234-235]等。抽样方法可以分为离线学习抽样和在线学习抽样。对于离线学习所构建的代理模型，模型的精度对优化的结果至关重要。优化设计效果很大程度上依赖于所构建的代理模型精度。为了改善这种离线模型精度问题，研究者提出了一些新的改进方法，以达到提升优化效果的目的。例如，基于代理模型的多步优化方法[236]、迭代响应面方法[237]、多代理模型方法[238-239]、迁移学习方法[240]等。在线构建代理模型的思路是在构建初始的代理模型基础上，根据优化过程中的优化数据，在线、自适应地更新代理模型。相比于离线建模，自适应地构建代理模型建模好处是：无需建立全局的近似代理模型，在优化过程中，自适应代理模型只需在重要的区域特别是最优解附近具有高的近似精度，这样在保证模型精度的同时也可以减少构建模型的样本点数[241]。在自适应SBO优化框架中，优化加点准则对自适应代理模型算法的优化效果至关重要。加点准则需兼顾最优特性及不确定度最大原则。目前，各种各样的加点准则得到了充分的发展，例如，最小化准则、EI准则、PI准则、MSE准则、LCB准则，以及不同种加点准则的并行融合[242-244]，可显著影响气动优化设计效率及效果。另外，多精度代理模型方法也是当前提升气动优化效率的研究热点[245-252]。

随着飞行器精细化设计需求的不断提高，气动设计所面临的复杂度提升，单独气动设计并不能满足实际工程需求，需要考虑多学科、多物理场之间的耦合作用，如飞行器气动-结构耦合设计、气动-噪声耦合设计、飞行器-发动机耦合一体化设计、气动-隐身的耦合设计等。这些工程需求势必会大幅增加气动优化设计难度，主要面临以下几个方面的技术难题：

1) 高维、精细化工程设计面临的海量计算。精细化设计势必要求高精度CFD评估，而高精度的CFD势必会大幅增加气动性能评估的计算时间。所以，如何继续提升优化设计效率的问题仍旧是值得关注的问题。另外，高维设计变量造成建模难、优化难、设计效果不佳，导致设计品质及优化效率大打折扣的问题[253]。

2) 基于不确定性的气动优化设计问题。近年来，虽然基于不确定性的气动优化方法得到了发展，但仍面临着高维不确定性参数，不确定性传播分析需要工程评估次数随着维数指数增长。

3) 对于复杂的工程气动设计，仍非常依赖专家或设计师经验，仍需要大量“人在回路”干预[254]。如何进一步减弱”人在回路”干预，在气动设计自动化的基础上，提升气动设计优化的智能化水平是一个值得研究的问题。

人工智能技术的发展，为解决上述所面临的实际工程问题提供了很好的技术支撑。人工智能技术与气动外形优化技术的深度融合，具体的促进作用表现为两方面：一是利用人工智能中相关机器学习方法所具备的强大算力，增强气动优化方法的设计能力，提升复杂工程优化设计品质并提升优化效率，如高维设计问题、不确定性设计等问题。二是利用人工智能技术能够模拟气动设计过程中专家的知识及经验，提升气动优化设计的智能化水平，实现气动设计自动化到智能化的跨越。未来的智能化研究可以关注如下两个方面：

1) 利用人工智能相关的机器学习技术，发展基于机器学习的气动外形设计方法、增强气动优化能力，提升优化设计品质和效率。可开展基于集成学习、主动学习、迁移学习等手段的气动外形优化设计方法，提升设计效果及效率。对于高维设计，可从稀疏学习、流形学习、特征分析的角度实现设计空间分解或分层设计策略以提升优化效果及效率。对于高维不确定性问题，可研究稀疏学习的高效不确定性传输及优化设计。

2) 利用人工智能技术替代专家经验，减弱“人在回路”作用，提升智能化气动设计水平。可开展流动网格自适应智能变形甚至是拓扑变形的研究，大幅增加变形空间；可开展多目标、多约束的自主智能化分配技术，实现优化进程根据实际需求自主变更目标及约束；可开展优化进程关键流场信息知识的学习及辨别方法的研究，从流场信息中挖掘关键信息，实现数据驱动的优化进程自我干预、自主调节智能化气动设计。

3.3 智能化、自适应流动控制

主动流动控制(Active Flow Control，AFC)，特别是闭环控制，是一个极具挑战性和实际意义的问题，应用在许多领域。近些年来，流动的主动闭环控制研究取得了很大进展，研究者们采用了各种各样的控制策略。由于对N-S方程离散将会导致系统维数达到105以上，而实用的控制器阶数远小于此，目前获得可用的控制器主要有两种思路[209]：第1种是“reduce-then-design”，首先建立一个能再现原系统输入输出特性的低阶模型，常用的方法有基于流场特征提取类方法，如本征正交分解法[113](Proper Orthogonal Decomposition, POD)和动模态分解法[116](Dynamic Mode Decomposition, DMD)，基于系统辨识类方法,如Volterra级数模型、ARX模型和ERA模型[255]，然后在此低阶模型基础上，开展低阶控制器设计[209, 256-257]；第2种是“design-then-reduce”，首先基于原全阶系统设计一个高阶的控制器，然后对此高阶控制器进行简化，得到一个实用的低阶控制器[258-259]。

在流动控制中，“reduce-then-design”因其计算上的优势而成为最常用的方法，而设计高维控制器大大限制了第2种方法的使用。但即使采用第1种方法，也面临以下问题：① 复杂流动具有不稳定、非线性、非定常的特点，其低阶线性模型难以获得，即使获得了复杂流动系统的开环低阶线性模型，针对其设计的控制律也不能保证能够用于原高维流动的闭环系统[260-261]；② 控制律的鲁棒性与自适应能力，由于真实流动环境中的不确定性以及其他因素的扰动，流动状态会发生变化，针对实际流动系统设计的控制律需要考虑到这些扰动，自动适应流动状态的变化，而传统主动控制方法不能兼顾控制的效果与鲁棒性。

近年来，数据驱动方法和机器学习的应用取得了很大的进展，由于数据驱动和机器学习的方法适合用于非线性、高维、复杂的问题，因此，它们也有希望解决流动控制中的难题。研究者们针对流动系统的智能化控制已经开展了不少工作，主要包含以下几个方面：

1) 基于模糊控制和神经网络控制的智能化流动控制方案

首先是早期基于模糊控制和神经网络控制的一些工作。模糊控制是以模糊集合论和模糊逻辑推理等为理论基础，不依赖被控制对象的精确数学模型，但有来源于专家经验的控制规则或者模糊表述的被控对象，研究者们结合模糊控制与神经网络、滑模变结构控制等其他方法开展了一系列研究，包括抑制圆柱尾迹的不稳定漩涡脱落[262]，抑制两自由度圆柱的涡激振动[263]，消除阵风对风能转换系统输出功率的影响[264]等。

在神经网络控制方面，Lee等[265]开创了神经网络在湍流闭环控制的探索。在低雷诺数湍流管道的直接数值模拟中，通过对神经网络结构和参数的优化，仅根据壁面的测量量对壁面进行吹吸，可以减少多达20%的表面摩擦力。Kawthar-Ali和Acharya[266]开发了一种神经网络控制器，用于抑制俯仰翼型前缘周期性发展的动态失速涡，根据非定常压力场来确定前缘吸力控制量，有效地抑制了涡流。近期，Ren等[267]基于径向基函数神经网络，提出一种数据驱动的跨声速翼型抖振自适应控制方法，结果表明这种控制方法可以在很大的流动范围内，完全抑制跨声速抖振载荷。

2) 基于遗传编程的智能化流动控制方案

近年来基于遗传编程(Genetic Programming，GP)的控制律设计方法逐渐被人们用于流动控制中。遗传编程是一种优化输入输出映射结构和参数的进化算法，将GP用于迭代学习和优化控制律，如图21所示[8]。其思路是将控制问题定义为一个最小化惩罚函数的问题，基于惩罚函数的值来判断给定控制律的性能，采用遗传编程作为搜索算法来最小化惩罚函数，优化控制律。控制律表示为递归表达式树，树的根是控制信号b，叶子是传感器矢量s或常数，表达式树通常由多个基本函数组成。这些函数可以接受任意数量的参数，但只返回单个值，例如，函数节点是+-×/, sin, tanh等，函数的参数可以是叶或子树，如图22所示，这些控制律作为遗传编程中某一代的一个个体。

图21 基于遗传编程的无模型智能化控制设计思路[8]Fig.21 Design of model-free intelligent control strategy based on genetic programming[8]

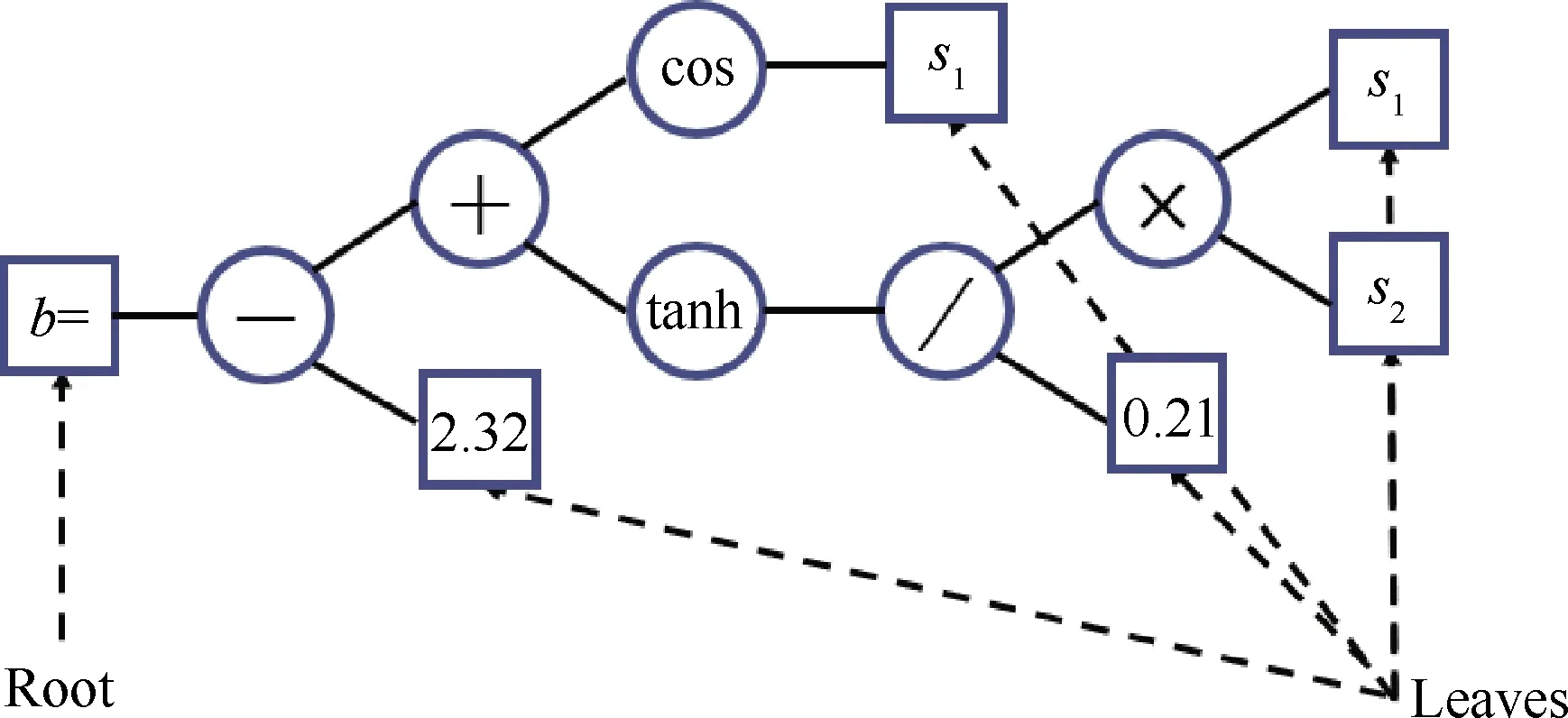
图22 递归表达式树对应的控制律表达式(b=K(s)=cos(s1)+tanh((s1×s2)/0.21)-2.32) [8]Fig.22 Control law representation based on recursive expression tree (b=K(s)=cos(s1)+tanh((s1×s2)/0.21)-2.32)[8]

基于遗传编程方法的主动控制策略广泛应用于工程中[268-269]，这种方法具有如下特点[270]：① 在 控制律优化过程中，GP方法不仅能够获得已知的典型控制规律，甚至可以发现新的控制方案；② 作为一种全局优化方法，GP方法不依赖初代控制律；③ 对优化参数变化不敏感；④ 适用于控制律搜索空间非常大的情况。

在流动控制领域，Duriez[271]和Gautier[272]等最先将该方法用于实验中后台阶流动的控制，使再循环区域缩小了80%，并且在一定范围内增加或减少雷诺数，基于遗传编程方法得到的控制律鲁棒性明显优于开环控制。此后，Debien等[273]将该方法用于减缓斜坡下游湍流边界层的分离；在湍流混合层研究中，Parezanovi等[274]证明该控制方案可以找到与基于降阶模型的反馈控制相同的最优控制信号，并且在改变来流速度时的鲁棒性显著优于开环控制；在增强湍流射流掺混方面，Zhou[270]和Wu[275]等采用6个独立的径向微射流装置，通过1 100次的优化学习，使得掺混率相较单一开环控制模式提高了一倍左右，并且发现在控制律的优化过程中，GP方法先获得了传统单一模式的开环控制律，最后掺混率进一步提高，控制律收敛到不同单一模式组合得到的新模式；Li等[276]通过对遗传编程进行改进，对一款车型进行闭环控制测试，实现减阻22%。Ren等[277]最先在仿真环境中实现基于遗传编程的主动控制，针对低雷诺数圆柱扰流，应用该控制策略能够抑制94.2%的涡致振动幅值，Noack[278]指出大多数控制律是在1 000个左右的测试评估中获得的，每个评估仅需在风洞中进行几秒钟。对这种方法的详细描述可以参考Duriez等[8]的著作。

3) 基于强化学习的智能化流动控制方案

随着强化学习(Reinforcement Learning, RL)的不断发展，强化学习已成为越来越多领域解决问题的基本模式。如图23所示，在强化学习的视角下，流动控制系统是通过3个简单的通道相互作用组合而成：① 观察，在每个时间步内，控制系统通过观察流动环境获得状态st∈S(例如一系列点的速度测量值)，S为可能的状态集；② 动 作，选择一个动作at∈A(st)(这里是主动控制量)，A(st)为状态st下可能的动作集；③ 报酬，执行控制动作at后，在下一时刻，控制系统收到一个报酬值rt+1∈R，R为实数集。控制的目标就是训练一个人工神经网络找到闭环控制策略，使得系统报酬总和最大(或最小)。Rabault 等[279]指出在学习任务的复杂度和学习速度方面，强化学习已经超越了遗传编程等方法，并将深度神经网络和强化学习引入主动流动控制领域，针对Re=100的圆柱绕流，采用零质量射流作为作动器，通过强化学习得到的控制策略与非定常尾迹相互作用，成功地稳定了涡街，并使阻力减小约8%。同样将强化学习用于圆柱绕流减阻的还有Guéniat等[280]，除了用于流动减阻，基于强化学习的控制方法还可用于研究流动环境中最优游动行为[281]。

图23 基于强化学习的流动控制系统原理图Fig.23 Schematic for flow control based on reinforcement learning

4) 其他智能化流动控制方案

除了上述智能控制方法外，Nair等[282]还提出了一种基于聚类的无模型自学习非线性反馈流动控制策略，针对NACA0012翼型的二维和三维分离流控制，在攻角为9°、雷诺数Re=23 000和来流马赫数Ma∞=0.3时进行了大涡模拟。在翼型前缘采用执行机构进行吹吸气，使用优化后的控制律针对二维翼型实现减阻41%，有效地降低了飞行功率消耗。

如表4所示，从目前的研究来看，早期基于模糊控制的流动控制策略不依赖于流动系统的精确数学模型，适用于非线性、时变、滞后、模型不完全系统的控制，就控制效果来看，相比于PID控制，模糊控制能够适应流动参数的变化，但由于模糊控制系统的非线性和多参数特性，参数整定过程在实际应用中很难实现，而且存在控制精度低、控制规则库庞大等缺点。基于遗传编程的控制律设计方案简单通用、鲁棒性强，并且对非线性复杂流动控制问题显示出很强的求解能力，因而被成功地应用于数值仿真和实验中，并且在近几年中得到了更深入的研究。但控制律的获取需要经过O～(103) 量级的控制律评估，限制了这种方法在数值仿真环境中的应用。相比于基于遗传编程的控制律设计方法，基于强化学习的控制律设计方法在流动控制任务的复杂度和控制律学习速度方面有所提高，在控制结果方面，其鲁棒性与控制效果均好于最优的开环控制，因此也得到越来越多研究人员的青睐，但强化学习的计算成本仍然是限制其广泛采用的主要原因，Brunton等[2]指出，这或许可以通过强化学习固有的并行性来解决。

表4 智能化流动控制方案对比Table 4 Comparison of intelligent flow control methodologies

流动控制的智能化和自适应化是未来发展的重要方向，目前智能化控制工作有待深入，主要集中在以下几个方面：

1) 复杂流动的高效鲁棒闭环控制律设计是流动控制方向的一个难点，首先是降低智能化控制律设计的计算成本，除了借助于人工智能的并行性以外，将流场特性与神经网络结构的优化相结合，如采用循环神经网络，长短时记忆神经网络等，也有可能为流动系统的智能化控制提供新思路；其次，真实的流动控制中，不可避免地存在噪声、时滞等问题，在控制律设计时需要将这些因素考虑到。

2) 智能化的流动控制还需要新型驱动机构、作动理念创新设计的支持，新型的作动器一直驱动着流动控制研究的发展，例如涡流发生器、各种射流技术、等离子体、记忆合金、壁面微结构与新材料等。但总的来看，除了涡流发生器这种被动方法在航空航天工程中有一定应用外，其他的技术应用较少，更多地集中于新概念的探索上。

3) 探索具体流场对驱动形式、作动器位置的敏感性评估方法，伴随方法、自动微分技术与流动的稳定性分析结合可以开展一些方法上的研究，为主动控制的先验设计提供物理指导。

4 总结与展望

人工智能为流体力学的发展提供了新的研究范式，流体力学为人工智能的发展提供了足够复杂的研究对象，传统学科和新型学科交叉融合、相得益彰。本文从智能赋能流体力学新的视角系统地总结了近年相关研究进展，并对智能流体力学研究的难点和发展趋势进行了简要展望。其学科内涵是以数据驱动形式为主要研究手段，采用机器学习等智能化方法去探索研究流体力学的新理论、新模型和新方法，发展针对流动信息的特征提取和数据融合方法，并推广数据驱动的方法在多场耦合、多学科设计和流动控制等方面的应用。智能流体力学未来的发展不仅要紧密借鉴人工智能新方法和新理论，还要紧密结合工程问题的实际需求，去攻克流体力学领域悬而未决的科学问题和工程设计面临的卡脖子难题。未来的研究需要关注以下几个方面：

1) 在充分利用经典流体力学研究方法和成果的基础上结合人工智能技术，不能脱离流体力学学科特点和背景。流体力学研究者在本领域还应发挥主导作用，特别是在问题的提出和架构设计上，而人工智能专家可以在方法和技术途径上起到支撑和指导作用。

2) 流体力学大数据小样本这一研究客观环境的机器学习和建模问题。与互联网大数据不同的是，虽然流体力学试验和计算中产生了海量数据，但这些数据是在特定边界条件下的数据，与流动状态、几何边界条件的高维度以及流体力学固有的高维、跨尺度、随机、非线性特征相比，很多情况下本质上是一个小样本问题。如何在小样本下开展机器学习本身就是人工智能领域面临的难题，就流体力学而言，有限的样本如何和已有的知识(包括守恒方程、量纲、标度、经验模型等)进行结合，在特征构造、模型架构设计以及参数寻优等方面发挥作用，才能有效解决流体力学大数据小样本下的机器学习难题。

3) 提升智能赋能流体力学的可解释性，探索流体力学新的物理内涵和科学认知。以神经网络为代表的黑箱模型和统计机器学习方法暴露出缺乏解释性、稳定性差等不足之处，特别是近年在流体力学机器学习研究中表现得特别突出，已经成为智能化方法和模型应用的瓶颈。如何有机结合现有流体力学知识和大数据，有机结合符号学习和统计学习这两类不同的机器学习方法，来提高智能模型的可解释性，进一步探索流体力学更加基本的物理内涵和科学认知，是未来需要着重加强的方向。

致 谢

本文源于2018年中国空气动力学会在清华大学举办的第十次钱学森学术讲座的特邀报告，因此首先感谢中国空气动力学会的邀请。其次感谢航空学报编辑部推荐本人作为《航空学报》“人工智能与航空航天专刊”的执行主编，促使本人对国内外有关智能赋能流体力学的研究进行进一步梳理，并整理成文。高传强、邬晓敬、王旭、朱林阳、王梓伊、曹文博、任凯，豆子皓、骆府庆、孙旭翔等多位青年教师和研究生参与了文献的收集和梳理，在此一并表示感谢！