基于综合应力工作态试验和神经网络的CMG失效边界域预测
黄首清,刘守文,翟百臣,周原,*,黄小凯,秦泰春
1. 航天机电产品环境可靠性试验技术北京市重点实验室,北京 100094 2.北京卫星环境工程研究所,北京 100094 3.北京控制工程研究所,北京 100190
控制力矩陀螺(Control Moment Gyroscope, CMG)是一种航天器姿态控制的惯性执行机构,相对于飞轮执行机构具有力矩放大效应,从框架输入很小的力矩就可以通过转子角动量方向的改变输出较大的姿态控制力矩[1],且控制精度高。CMG在需要快速机动和高指向精度的航天任务中获得广泛应用[2]。CMG结构复杂,内部有高速旋转轴系,真空、冷热交变等工作环境会影响轴系转动的工作寿命和可靠性,严重时甚至可能造成CMG在轨失效。例如1973年美国“天空实验室”(Skylab)的两台CMG在轨飞行6个月后相继出现问题,1号CMG率先发生异常并最终失效,不久2号CMG也出现异常,均与在轨复杂动力学工况下的运动部件热变形和磨损有关[3]。国际空间站的1号CMG也曾发生异常温升和振动,最终完全失效,3号CMG也曾发生间歇性故障,最终不得不在轨更换2个CMG组件[4]。对于CMG这种运动特性突出且结构复杂的组件,地面试验是了解其工作特性的重要途径。常见的地面试验包括热真空试验和寿命试验,但是试验开销很高,且难以真实模拟在轨状态,尤其是CMG的运动工况。综上所述,设计地面试验真实模拟CMG的在轨工作状态,并尽可能提高试验效费比,对快速摸清CMG的失效边界域,确保使用可靠性并指导产品设计改进具有重要意义,也是践行实战化“试验鉴定”理念[5-7]和响应国家“质量强国”战略需求的有益尝试。其中失效边界域[8-9]是航天型号研制中的一个重要概念,指航天器产品在多种工作应力组合下工作极限的包络,只有产品工作应力组合在这个包络以内才会处于有效和安全的工作状态。目前CMG的失效边界域常常基于大量的试验取得,时间和经费开销较大,只通过少量试验的方式预测失效边界域将是未来技术发展的重要趋势之一。
在提高地面试验的真实性和效费比方面,前人做了很多工作。美军DOD-HDBK-343手册[10]以及近年的作战试验与试验鉴定年报[11-13]中对空间试验项目的核心要求之一便是“Test it like you fly it”(像飞行一样进行试验),或尽可能在飞行任务配置下进行模拟实际[14]的地面试验。虎刚等[15]设计了某CMG的热平衡试验,通过对161个温度测点的数据分析研究了工作温度范围内不同环境温度下的热特性。魏大忠等[16]设计实施了天宫一号CMG的力、热环境试验和超过52个月的寿命试验,监测了转速、电流、温度、振动等参数,没有发现明显性能退化。虚拟仿真试验是提高效费比的重要研究手段,刘守文等[17]通过热-结构耦合仿真定位了某CMG框架启动困难和运行卡滞现象的发生机理。王雅梦[18]利用有限元法和热流网络平衡法建立了CMG轴承组件的温度场模型,研究了不同工况、温度和电机功率对温度分布的影响。此外,正交试验和人工智能方法也被用于提高试验和仿真研究的效费比。张俊红等[19]利用正交试验方法优化了影响轴承润滑特性的13个参数,显著降低工作量并可满足精度要求。单钧麟等[20]利用粒子群算法优化控制器的权重系数矩阵,使系统具备一定的抗干扰能力。MacKunis等[21]将神经网络方法用于CMG控制模型,试验证明可以更好地适应外部扰动力矩。但是,目前神经网络等人工智能方法主要用于优化CMG的控制算法[22],在试验方法和优化方面尚无应用。
针对目前的研究现状和趋势,本文设计了一种可同时模拟真空热环境和CMG与航天器角动量交换工况的试验设备并提出了CMG的综合应力工作态试验方法,并基于少量试验结果和神经网络方法对CMG的工作极限转速矩阵、失效边界、失效边界域进行预测,可以在更真实模拟CMG在轨工作状态的同时显著节省试验经费和时间,并具有较高的预测准确性。此外,神经网络模型的特点也决定了所提出方法适用于复杂多应力、多因素耦合的场景,并将随着有效试验数据的积累将体现出更好的适用性和准确性。
1 CMG综合应力工作态试验
1.1 试验设备
参考图1,所研究的CMG主要由转子组件和框架组件组成,转子组件提供恒定的角动量,框架组件驱动转子组件转动以改变角动量方向,输出陀螺力矩,同时与航天器实现角动量交换。为了较真实地模拟CMG的在轨实际工况,设计了转台模拟航天器与CMG的角动量交换,利用KM2E空间环境模拟器模拟在轨真空热环境。这样,试验中同时模拟温度、CMG框架转速、航天器转速3种应力,且在真空环境下开展试验,即CMG综合应力工作态试验。

图1 CMG综合应力工作态试验设备示意图Fig.1 Test equipment for combined stress working-state test of CMG
试验中的温度应力可超出CMG的工作温度范围(0~45 ℃),框架转速和转台转速也可超出工作转速,以获得极限应力下的潜在故障和CMG的失效边界。整个试验系统主要由KM2E环境模拟器、对接小车、转台、产品工装、红外笼等组成。其中,KM2E环境模拟器主要用于提供试验所需的真空冷背景环境;对接小车用于转台、红外笼和试验线缆等试验设备的承载和固定;红外笼用于试验产品的加热和升温;转台用于对CMG试验产品提供旋转载荷以及角动量交换;产品工装用于CMG试验产品与转台间的连接和固定,保证CMG在试验过程中的安装姿态,并对试验线缆起辅助固定作用。
1.2 试验设计
试验方案如下:真空度:优于1.3×10-3Pa;温度台阶(由于试验耗时过长,只完成一部分温度台阶):-35 ℃、-30 ℃、-25 ℃、-20 ℃、-15 ℃、-10 ℃、-5 ℃、5 ℃、20 ℃、35 ℃、45 ℃、50 ℃、55 ℃、60 ℃;控温点:框架组件侧筋表面和CMG顶部;温度允差:±2 ℃;热沉温度低于100 K,热沉黑度大于0.9;转台转动条件:每个温度下,转子转速6 000 r/min,CMG框架转速包括5 (°)/s、10 (°)/s、 20 (°)/s、24 (°)/s、30 (°)/s、40 (°)/s、50 (°)/s 和57.3 (°)/s共8种,转台转速包括0 (°)/min、 1 (°)/min、2 (°)/min、3 (°)/min、4 (°)/min 和5 (°)/min共6种,对各种CMG框架转速和转台转速做排列组合,每种组合下连续运行1 h以上直到控温点温度稳定。
1.3 试验结果
试验中发现的主要潜在故障主要包括CMG框架启动困难和运转卡滞,例如图2是典型的框架启动困难现象,在陆续发出-5 (°)/s、5 (°)/s、10 (°)/s、20 (°)/s转速指令后,CMG框架才正常启动。图3是典型的框架运转卡滞现象,框架运转偶尔发生持续十几秒的停顿,然后自我恢复。
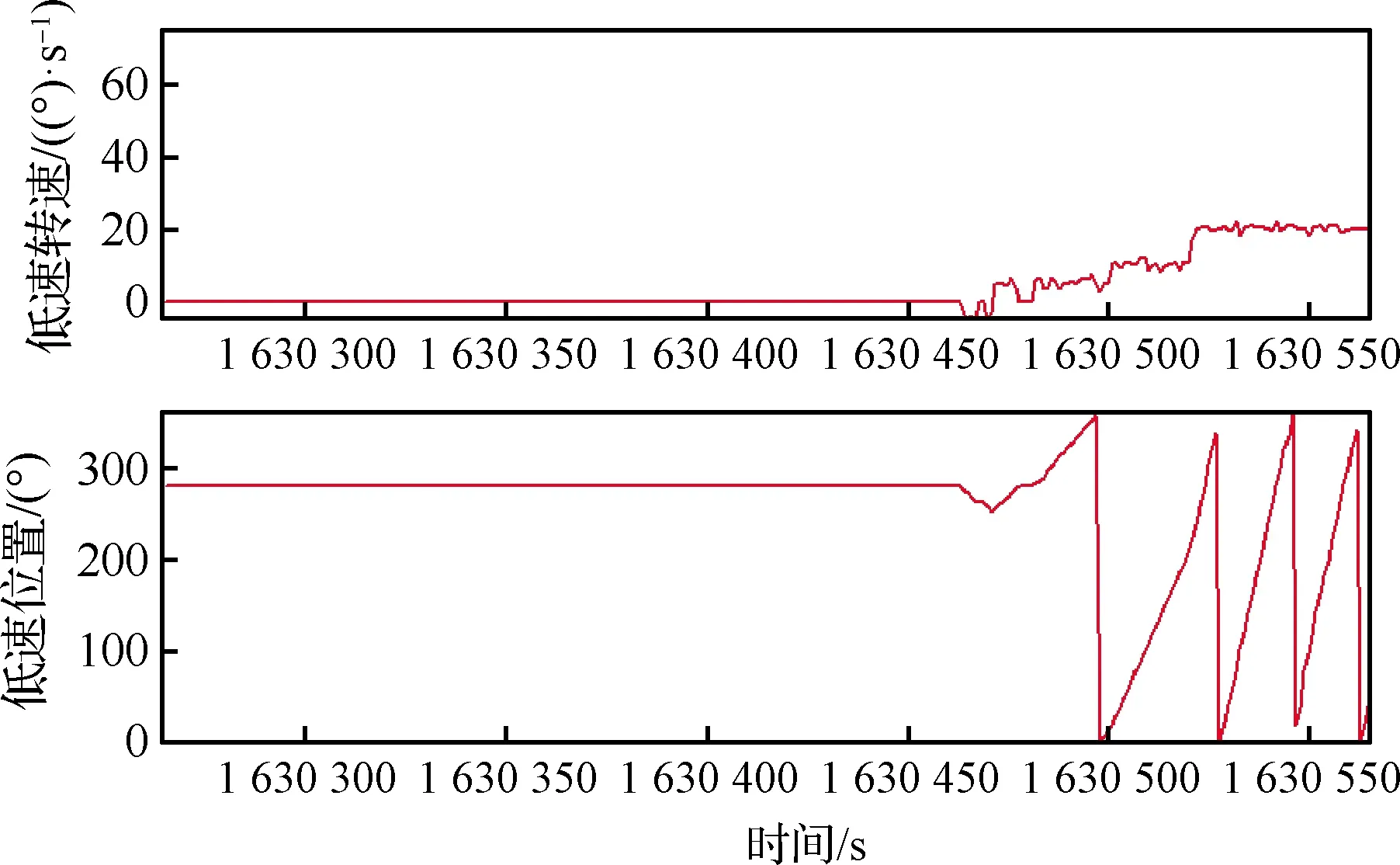
图2 典型的CMG框架启动困难现象Fig.2 Typical CMG frame start-up hesitation phenomenon

图3 典型的CMG框架运转卡滞现象Fig.3 Typical CMG frame rotation break phenomenon
需要指出的是,这些潜在故障发生在CMG的工作温度范围或工作框架转速以外,虽然并非实际工作情况,但却蕴含着产品的失效边界信息。通过对上述试验过程及现象进行总结分析,可得到CMG在多应力综合环境作用下的极限转速应力矩阵,部分试验结果如表1~表4所示(表中ωg和ωs分别代表CMG框架转速和转台转速),并做如下说明:
1) “×”代表经试验验证在该转速组合下CMG无法长时间稳定运行,“√”代表经试验验证在该转速组合下CMG可以长时间稳定运行,“√/”代表经试验验证在该转速组合下CMG只能短时间正常运行;深灰色区域代表推断在该转速组合下CMG无法长时间稳定运行,浅灰色区域代表推断在该转速组合下CMG可以长时间稳定运行,白色区域代表无法给出推断结果。
2) 随着CMG低速框架转速提高,CMG低速框架发热量增加,温度梯度和热变形加剧;随着转台转速提高,CMG低速电机上受到的耦合力矩增加。据此可以推断,在外界温度环境保持不变的情况下,若CMG在某一个转速组合下无法长时间稳定工作,则其右下方矩形区域内的转速组合均无法稳定工作;反之,若CMG在某一个转速组合下可以长时间稳定工作,则其左上方矩形区域内的转速组合均可以稳定工作。表1~表4中深灰色和白色区域正是根据本条规律推断,“D√”和“D×”分别代表推断该转速组合下可以长时间稳定运行和无法长时间稳定运行,这些数据代表了工程经验,并非直接的试验结果。

表1 55 ℃下CMG长时工作极限转速矩阵
3) 由于一个温度下的CMG长时工作极限转速矩阵的获得极其耗费时间,因此仅完成20 ℃、35 ℃、45 ℃工况下的CMG长时工作极限转速矩阵,且可以据此绘出3种温度工况下的转速失效边界(表中粗线);而55 ℃工况下的试验数据过少,无法准确判断失效边界。

表2 45 ℃下CMG长时工作极限转速矩阵

表3 35 ℃下CMG长时工作极限转速矩阵

表4 20 ℃下CMG长时工作极限转速矩阵
2 神经网络模型
2.1 结构和算法
基于误差反向传播 (error Back Propagation, BP)神经网络进行建模。本文基于MATLAB2019a神经网络工具箱建立的BP神经网络(简称神经网络)包括输入层、输出层和隐层。其中,输入层共3个神经元,分别输入控点温度、CMG框架转速和转台转速,输出层共1个神经元,输出CMG运行状态,根据经验公式[23]确定隐层神经元个数:
kh=2ki+1
(1)
式中:kh为隐层神经元个数;ki为输入层神经元个数,因此隐层神经元个数取7。这样,所建立的神经网络结构如图4所示。其中,神经元传递函数为双曲正切的S型Tansig函数;训练函数为Trainlm,即Levenberg-Marquardt算法;神经网络预测性能用MSE和R评价,分别是样本输出值与预测值的均方误差以及回归相关系数。
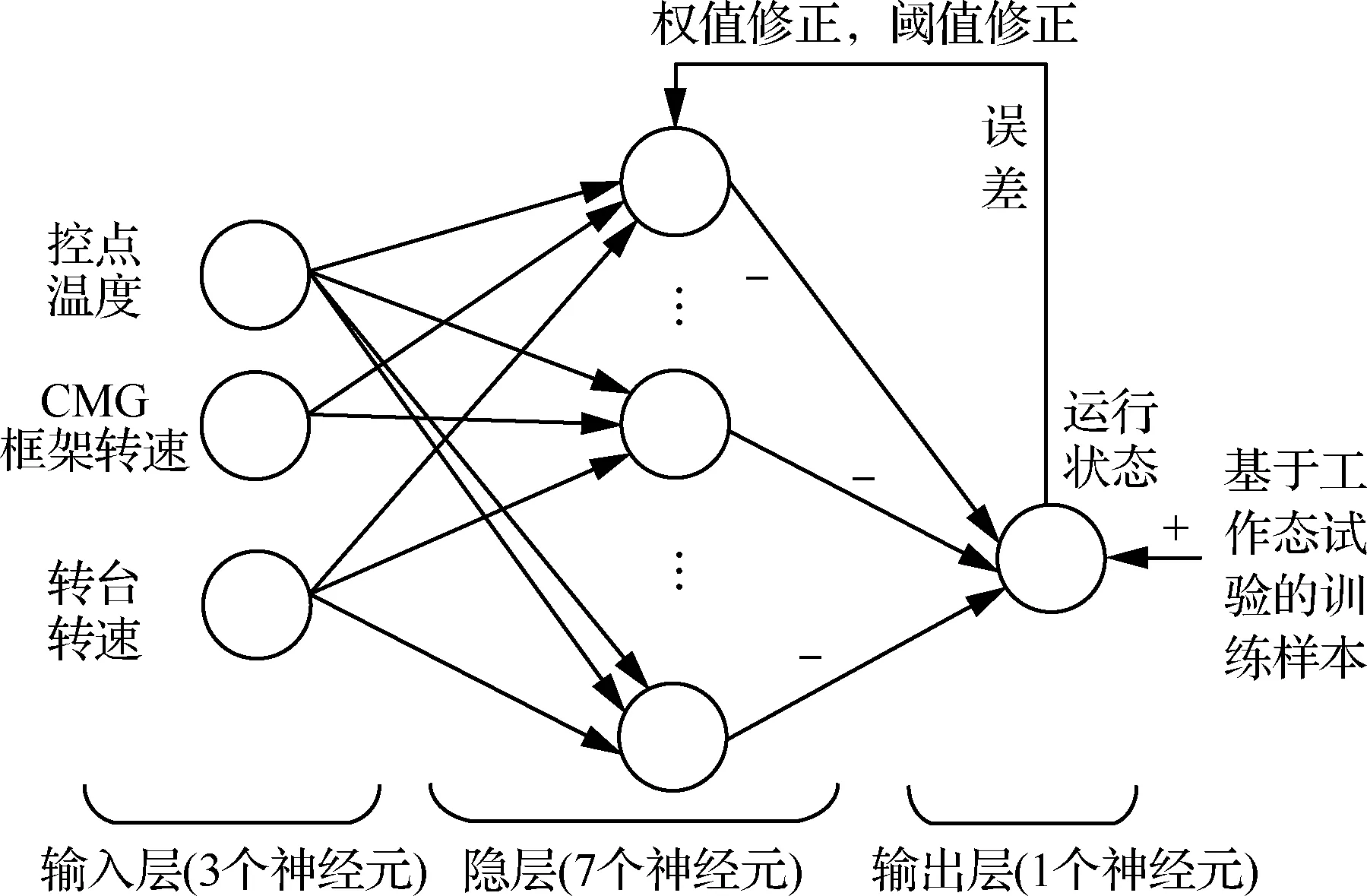
图4 用于预测CMG运行状态的神经网络结构Fig.4 Neural network structure for CMG running status prediction
(2)
(3)
式中:n为样本数量;xi和yi分别为样本输出值和预测值;μx和σx分别是样本输出值的均值和标准差;μy和σy分别是预测值的均值和标准差。
2.2 运行状态的定量表达
CMG运行状态的是个典型的离散型结果,即只有“无法长时间稳定运行”、“可以长时间稳定运行”和“只能短时间正常运行”3种运行状态,而神经网络的输出结果常常是连续变量。如何让神经网络识别这3种运行状态并作为训练数据读入神经网络,如何将神经网络的输出结果再映射回这3种运行状态是神经网络训练和泛化预测需要解决的问题。考虑到神经网络预测初值P0表示对应输入应力组合下CMG可以长时间稳定运行的倾向性,因此将训练数据中的“无法长时间稳定运行”、“可以长时间稳定运行”和“只能短时间正常运行” 3种运行状态分别对应输出值0、1和0.5, 而将神经网络泛化预测初值P0做如下处理映射回上述3种运行状态:
(4)
2.3 模型训练
为了便于对比研究,这里取具有不同数据量的2类典型训练数据集I和II见表5,区别在于是否包含经验样本。

表5 两类训练数据集Table 5 Two data sets for training
2类训练数据集I和II中,又分别包括用于训练权值与阈值的训练样本、用于训练各隐层神经元数量的验证样本和用于评价对其未见过数据泛化预测能力的测试样本。训练样本、验证样本和测试样本均为随机选择,分别占80%、10%和10%。基于2类训练数据集的训练结果见表6,可见基于训练数据集I的训练效果最好(均方误差最小、回归相关系数最接近1),而训练数据集Ⅱ的训练效果稍差,但也达到了较低的均方误差和接近1的回归相关系数,可以认为基于两类训练数据集均可对神经网络进行较好的训练并用于泛化预测。

表6 训练数据集的训练结果Table 6 Training results based on data sets
以数据量较大的训练数据集Ⅱ为例,训练次数与均方误差的关系见图5,可见超过14次后,验证样本的均方误差基于稳定,可认为已经完成训练。而预测值与训练数据输出值的误差直方图和回归相关系数分别见图6和图7,图7中,Y为样本输出值,T为预测值,可见绝大部分样本的误差集中于零误差线附近,其中预测值与预测样本输出值的回归相关系数高达0.99,可以初步证明经过训练的神经网络具有较好的预测能力。
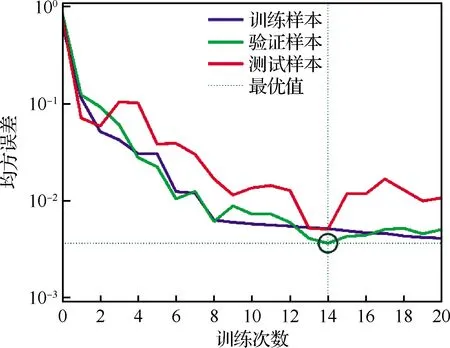
图5 训练次数与均方误差的关系Fig.5 Relationship between training iterations and MSE

图6 预测值与训练数据值的误差直方图Fig.6 Error histogram of prediction results versus data sets
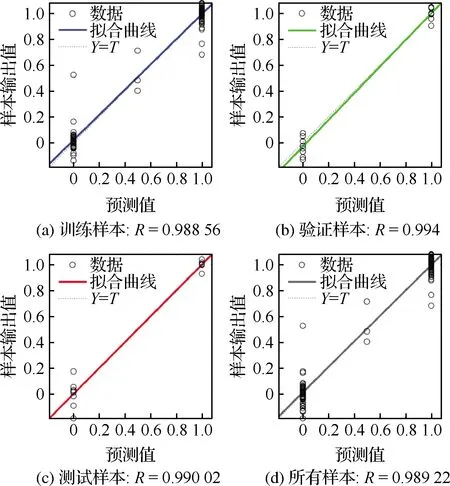
图7 预测值与训练数据值的回归相关系数Fig.7 Regression correlation coefficient of prediction results versus data sets
3 结果与讨论
3.1 工作极限转速矩阵的典型预测结果
表7展示了基于Ⅰ和Ⅱ两类训练数据集完成训练的神经网络对训练数据集数据进行预测的结果,分别可以获得100%和98.8%的正确率。以训练数据集Ⅱ为例,将据此训练的神经网络预测的工作极限转速列于表8,并可绘制失效边界(表中粗线)。对比表8和表1,可见基于神经网络的预测数据可以给出仅凭试验数据无法得到的55 ℃下的转速失效边界。需要指出的是,本文中神经网络的训练仅耗时3 s左右,基于训练后的神经网络获得预测数据几乎是瞬时完成的,而且理论上可以获得任意控点温度下的失效边界,这相对于传统的纯试验方式在时效性方面有极大优势,并且具有较高的正确率。

表7 典型训练数据的运行状态预测正确率

表8 基于训练数据集Ⅱ预测的55 ℃下CMG工作极限转速矩阵和失效边界
3.2 经验样本对预测结果的影响
训练数据集Ⅰ与Ⅱ的区别在于不包含经验样本,将基于训练数据集I完成训练的神经网络用于预测55 ℃下的极限转速矩阵,如表9所示。对比表8和表9可以发现,虽然训练数据集不同,但是训练出的神经网络预测出来的工作状态和长时工作极限转速边界是相似的,仅当CMG框架转速和转台转速组合在(24 (°)/s,2 (°)/s)、 (57.3 (°)/s,1 (°)/s)时不同。需要指出的是,训练数据集I在55 ℃下仅包含了4个样本点,而训练数据集Ⅱ则多出了24个经验样本却获得了相似的预测结果,这说明此类经验样本在预测CMG工作状态和长时工作极限转速边界时起的作用不大,即神经网络可以内化试验数据背后的工程经验。
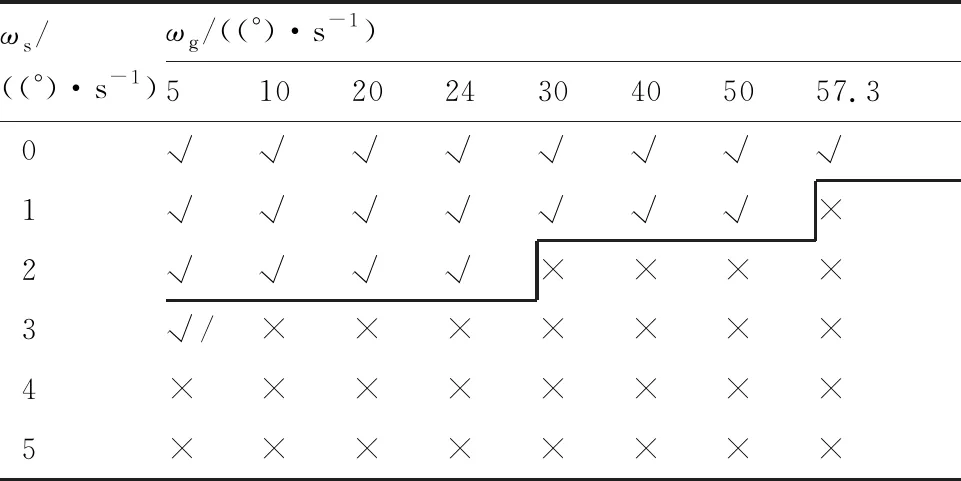
表9 基于训练数据集I预测的55 ℃下CMG工作极限转速矩阵和失效边界
3.3 失效边界域预测结果
整理神经网络的预测数据,综合20 ℃、35 ℃、45 ℃和55 ℃下的失效边界即可得到CMG在控点温度、CMG框架转速和转台转速3种应力下可以正常工作的应力极限包络,即失效边界域。图8是基于训练数据集I获得的失效边界域,形象展示了3种应力对应力极限的耦合影响。失效边域这一曲面内部可视为CMG可以正常工作的区域,而曲面外部则为不可以正常工作的区域。此外,可以看出在环境温度为35 ℃时,CMG框架转速和转台转速的工作域最宽;而随着CMG框架转速增大,环境温度和转台转速的工作域明显收窄;而随着转台转速增大,环境温度和CMG框架转速的工作域也明显收窄。
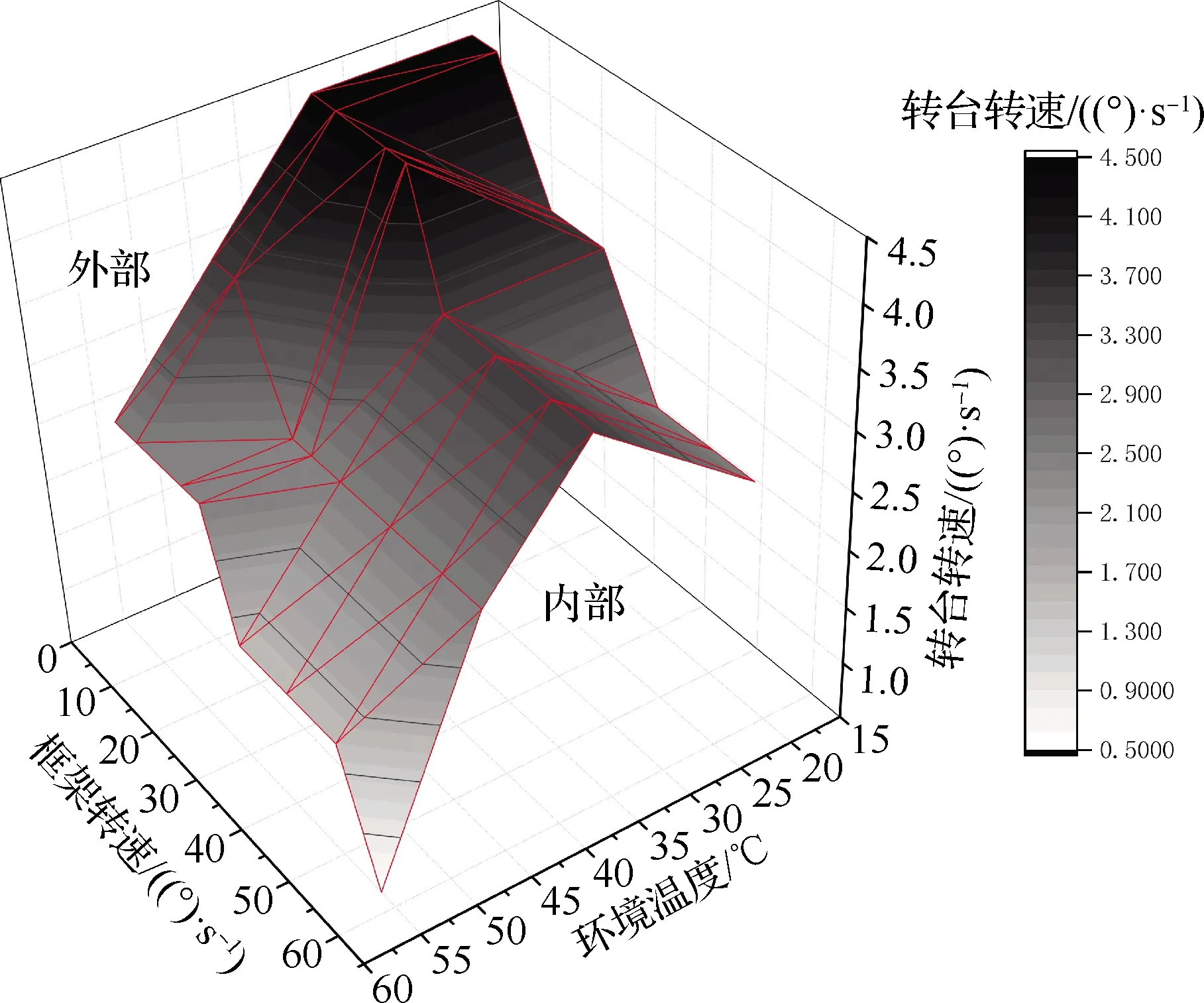
图8 基于训练数据集I的神经网络预测的 CMG失效边界域Fig.8 Failure boundary domain of CMG predicted by neural network based on data set I
界
3.4 预测结果的可信度分析
由于神经网络的预测结果是通过按照式(4)映射回“无法长时间稳定运行”、“可以长时间稳定运行”和“只能短时间正常运行”3种情况得到,那么对于同样的运行情况,神经网络的预测初值P0一般是不同的,一定程度上能反映预测结果的可信度。表10给出了基于训练数据集I预测的55 ℃下运行状态和初值(科学计数法表示),考虑到“只能短时间正常运行”为能否正常工作的过渡情况,本身就代表了一种不确定的状态,且对应输出值0.5。因此,可以认为越远离0.5的预测初值对应运行状态的可信度越高,以表10为例,框架转速和转台转速组合在(0 (°)/s,5 (°)/s)的预测初值5.47比(24 (°)/s,1 (°)/s)的预测初值1更远离0.5,因此(0 (°)/s,5 (°)/s)的预测结果更可信;而类似的,(5 (°)/s,5 (°)/s)的预测结果也比(40 (°)/s,2 (°)/s)的预测结果更可信。

表10 基于训练数据集I预测的55 ℃下运行状态和初值Table 10 Predicted running status and output initial values at 55 ℃ based on data set I
4 结 论
本文提出了CMG工作态试验设备和试验方法,给出了一种基于不完全试验数据和神经网络的失效边界域快速预测方法,分析结果表明该方法可以显著节省试验经费和时间,并具有较高的预测准确性,主要研究结论包括:
1) CMG综合应力工作态试验发现极限应力组合下某CMG潜在故障主要包括框架启动困难和运转卡滞,给出了20 ℃、35 ℃、45 ℃工况下的CMG长时工作极限转速矩阵。
2) 本文中建立的BP神经网络将泛化预测初值映射回“无法长时间稳定运行”“可以长时间稳定运行”“只能短时间正常运行”3种运行状态,并分别对应输出值0、1和0.5,解决了神经网络识别和预测3种离散运行状态的问题。
3) 完成训练的神经网络对Ⅰ和Ⅱ两类训练数据集分别可以获得100%和98.8%的预测正确率,可以给出仅凭试验数据无法得到的55 ℃下的转速失效边界,并且在时效性方面有极大优势。
4) 针对本文的神经网络模型,包含经验样本的训练数据集Ⅱ在预测CMG工作状态和长时工作极限转速边界方面相较不包含经验样本的训练数据集I并没有优势,体现了神经网络可以内化试验数据背后的工程经验,可以规避经验可能存在的主观性。
5) 通过神经网络模型预测的20 ℃、35 ℃、45 ℃和55 ℃下的失效边界可得到CMG在控点温度、CMG框架转速和转台转速3种应力下可以正常工作的应力极限包络,即失效边界域。在环境温度为35 ℃时,CMG框架转速和转台转速的工作域最宽;而随着CMG框架转速增大,环境温度和转台转速的工作域明显收窄;而随着转台转速增大,环境温度和CMG框架转速的工作域也明显收窄。
6) 提出了用神经网络的初值P0反映预测结果的可信度,越远离0.5的预测初值对应运行状态预测结果的可信度越高。
本研究尚有一些不足,例如单台CMG的数据代表性问题;以及神经网络模型存在过学习或欠学习现象,可能对预测结果有影响。作者将针对以上不足开展进一步的研究。

