基于径向基神经网络的气动热预测代理模型

张智超，高太元，张磊，拓双芬

北京机电工程总体设计部，北京 100039

高超声速飞行器气动热环境的准确预测对于飞行器热防护系统的设计至关重要。一方面，若飞行器表面的热流预测偏低，会严重危及飞行器的安全，甚至会导致飞行器的烧毁；另一方面，表面热流预测偏高，会造成热防护系统存在较大的冗余度，降低飞行器的有效载荷。然而，高超声速飞行器气动热环境的准确预测仍面临诸多难题[1]。在飞行器的气动热设计过程中，工程估算方法虽然速度快、效率高，但其针对非轴对称复杂外形的飞行器适应性较差、精度不足。风洞试验方法虽然能够较准确地预测飞行器模型在地面风洞的热环境，但目前风洞试验数据的天地一致性问题尚未完全解决[2]，并且受制于经费、试验周期等因素的限制，无法针对飞行走廊内全部状态开展大规模气动热环境的试验研究。目前，随着计算流体力学(Computational Fluid Dynamic，CFD)方法的迅猛发展，已经可以实现对高超声速复杂外形飞行器全尺寸流场的数值模拟，但沿全飞行走廊开展大规模数值计算的代价仍相当昂贵，也无法满足工程设计阶段对气动热环境快速分析的需求。因此，发展一种可达到与CFD方法相当精度的高超声速飞行器气动热环境快速预测方法，有效缩短飞行器气动热设计的周期，是目前高超声速飞行器气动热设计需要亟待解决的问题之一。

针对上述问题传统的解决方法是以试验或数值模拟数据为基础，通过拟合或回归预测方法以一定的精度逼近真实模型，得到飞行器气动参数的解析表达式[3]。然而，飞行器在不同状态下表面不同位置的气动参数难以用统一的数学关系式来描述，并且不同状态下对应的气动参数存在较强的非线性关系，采用传统的线性插值、回归方法难以保证精度。为此，Dowell[4]和Silva[5]提出了基于CFD数值模拟构造飞行器流场降阶代理模型(Reduced-Order Model，ROM)的思想。ROM是一类低阶的、具有一定计算精度并节约时间的数学模型[6-7]，该方法最初用于建立气动弹性问题中非定常流场的气动力辨识模型，此后在优化设计、实时仿真等领域也得到了重要的发展。传统的ROM代理模型常用方法有响应面、Kriging[8]、本征正交分解(Proper Orthogonal Decomposition，POD)[9]等，但这些方法大多要求训练样本数据库对输入的自变量尽可能采取正交设计方法，这导致获取训练样本所需计算量与自变量维度成几何量级式增长。

近些年，随着人工智能技术的快速发展，机器学习在算法、理论和实际应用方面都取得了巨大的成功，尤其是人工神经网络方法在气动建模与先进飞行器设计中也蕴含着巨大的应用价值[10-11]。相比于传统回归预测方法，神经网络方法无需事先确定输入和输出之间映射关系的数学方程，仅通过自身的训练，学习某种规则，在给定输入值时得到最接近期望输出的结构。利用多层神经网络方法进行回归预测，对样本点正交性要求降低，并且能够通过设计不同的神经网络结构和选用不同的激活函数来模拟逼近多种非线性关系，进而建立适用于飞行器气动参数辨识的代理模型。在国内，多位学者利用神经网络方法开展了气动力辨识代理模型的研究[12-17]。王孝学[12]利用自动增加隐藏节点的径向基神经网络对再入飞行器的气动力进行了辨识。张锋涛等[13]利用人工神经网络响应面方法，开展了乘波体飞行器优化设计研究。寇家庆和张伟伟[14]开展了基函数宽度对递归径向基(Radial Basis Function，RBF)神经网络气动力模型精度的影响研究。白俊强等[15]采用改进的RBF神经网络对翼梢小翼进行了优化设计。尹明朗等[16]发展了一种高泛化能力的神经网络气动力ROM模型。张栋[17]利用误差逆传播(error Back Propagation，BP)神经网络方法为故障飞行器建模获取了大量故障气动力系数的数据。需要注意的是，现有研究所建立的大多是气动积分力的代理模型，而飞行器表面的分布热流、压强等物理量由于数据量大且内部存在相关性，目前的建模研究尚较缺乏。

不同于传统气动积分力的预测，表面热流为分布量，每个飞行状态对应飞行器表面不同位置的热流不同。若采用单一神经网络，其输入变量给定为相应的飞行参数，输出变量给定为热流，则神经网络输出的热流也应随位置的不同而不同。因此，采用单一神经网络进行飞行器表面热流预测存在较大的困难。

本文将基于径向基神经网络发展一种适用于高超声速飞行器表面热流分布预测的代理模型方法，以实现对飞行器气动热环境的快速预测。第1节介绍了所采用的神经网络及在此基础上发展的气动热代理模型方法。第2节使用所建立的代理模型方法针对美国火星实验室的椭圆钝化外形飞行器开展训练建模，分析了基函数宽度对代理模型预测精度的影响以及代理模型泛化能力。最后，第3节给出了结论。

1 气动热代理模型的建立

为了建立气动热快速预测的代理模型，本文提出了一种采用多个离散位置的神经网络协同预测飞行器表面热流的方法：① 以数值模拟中飞行器表面网格节点为基础，在每个网格节点上均单独构造一个神经网络；② 每个神经网络的输入为飞行状态参数，输出为该飞行状态下当前网格节点的表面热流；③ 通过训练集对所有神经网络同时进行训练，获得各自网络的连接权值；④ 所有网格节点的神经网络协同预测飞行器表面的热流，获得气动热预测代理模型。

对于每个节点神经网络的设计，选择同一种网格结构形式以保持预测精度的一致性。在常用的前馈神经网络中，BP神经网络易限于局部极小值，学习过程收敛速度慢，并且隐藏层数量及各层神经元数难以确定。相比之下，RBF神经网络可以根据具体问题确定相应的网络拓扑结构，具有自学习、自组织、自适应能力，它对非线性连续函数具有一致逼近性，学习速度快。因此，本文对于每个节点的神经网络均采用了RBF神经网络方法进行设计。

1.1 RBF神经网络输入与输出的关系

人工神经网络方法从信息处理角度对人脑神经元网络进行抽象，按不同的连接方式组成不同的网络。神经网络由大量的神经元之间相互连接构成，每个神经元代表一种特定的输出函数，每2个神经元间的连接都代表一个通过该连接信号的加权值。网络的输出根据网络的连接方式、连接权值和激活函数的不同而不同。

RBF神经网络是由Broomhead和Lowe[18]首先提出的一种采用径向基函数作为激活函数的前馈神经网络，通过适当的训练，可以实现数据分类和函数逼近。典型RBF神经网络的基本结构如图1所示，其中d为输入矢量维数，q为隐藏层神经元数，l为输出矢量维数。RBF神经网络是一种单隐藏层的前馈神经网络，它使用径向基函数作为隐藏层神经元激活函数，而输出层则是对隐藏层神经元输出的线性组合。RBF神经网络共3层，分别为输入层、隐藏层和输出层。RBF神经网络不仅收敛速度高于传统的BP神经网络[19]，而且只要给定其隐藏层足够数量的神经元，则可实现以任意精度逼近某个函数[14]。

图1 典型RBF神经网络结构Fig.1 Structure of typical RBF neural network

输入变量首先通过RBF神经网络的输入层进入网络，经过隐藏层的激活函数完成非线性映射。随后，隐藏层的输出以不同线性加权的方式由输出层的各神经元实现线性映射。其中，隐藏层的激活函数一般采用高斯函数[14]。设输入矢量为x=[x1,x2,…,xd]，进入隐藏层后，在高斯函数的作用下发生如下变换：

(1)

输入变量经过由输入层至隐藏层的非线性变换后，得到隐藏层的输出向量B=[b1,b2,…,bq]T。然后，通过不同线性加权的方式由隐藏层，得到RBF神经网络输出层神经元的输出：

(2)

式中：yj为输出层第j个神经元的输出，输出层所有神经元的输出构成输出向量y=[y1,y2,…,yl]T；ωjh为隐藏层第h个神经元和输出层第j个神经元的连接权值，RBF神经网络训练的关键问题之一就是如何获取连接权的权值ωjh。若当前RBF神经网络隐藏层的输出为矩阵B，隐藏层至输出层的连接权值矩阵为ω，则对所有训练集样本，网络的输出为

(3)

则神经网络的实际输出与训练集的误差为

(4)

通过最小二乘法使ε最小化，可求出隐藏层至输出层的连接权值矩阵：

ω=B+y

(5)

式中：B+为B的伪逆，表达式为

B+=(BTB)-1BT

(6)

1.2 RBF神经网络的学习算法

在RBF神经网络中，输入通过隐藏层被映射到一个新的向量空间，输出层在新的向量空间中重新进行线性组合并进行输出。当隐藏层神经元的个数及高斯基函数中心和宽度等参数确定后，对连接权值的训练就可以采用线性优化方法，因而RBF神经网络可实现快速训练学习。构造和训练一个RBF神经网络就是要确定每个高斯基函数的中心ch和宽度σh，并通过适当的训练获得连接权值ωjh，实现输入到输出的映射。

一般地，RBF神经网络隐藏层节点的中心向量取自输入向量，通过逐个增加隐藏层节点，使均方偏差满足要求后完成网络设计，这种方法训练而成的神经网络被称为广义RBF神经网络。然而，现有研究[14]表明，正则化RBF神经网络在气动分析领域具有较高的优势，因此本文选择正则化RBF神经网络进行气动热预测代理模型训练。正则化RBF神经网络是创建一个精确的径向基网络，其隐藏层节点数目与输入样本相同，各个隐藏层中心即为各样本向量。正则化RBF神经网络隐藏层中心向量可直接确定为输入各样本向量，各隐藏层基函数采用均匀宽度，作为模型的超参数通过交叉试验法给出。在隐藏层基函数的中心和宽度确定后，隐藏层神经元的输出也随之确定。因此，隐藏层和输出层之间的权值ωjh可以通过有监督的学习规则计算确定，如线性最小二乘法或伪逆法。

至此，正则化RBF神经网络隐藏层神经元数量、隐藏层基函数中心和宽度、隐藏层至输出层权值均可以确定，进而可以建立气动热预测代理模型，模型建立过程如图2所示。

图2 气动热预测代理模型建立过程Fig.2 Establishment process of ROM model for aerodynamic heat prediction

2 代理模型方法应用验证

为了检验气动热快速预测代理模型的实际应用效果，本节选取了美国NASA火星实验室所设计的椭圆钝化高超声速飞行器[20]开展应用验证研究。

2.1 确定RBF神经网络的结构

NASA火星实验室所设计的椭圆钝化高超声速飞行器[20]几何尺寸如图3所示，其中L=0.304 8 m，anose=0.101 6 m，r=blower=0.050 8 m，alower= 0.025 4 m。

图3 飞行器几何外形示意图[20]Fig.3 Schematic diagram of geometric shape of hypersonic vehicle[20]

本研究利用自有的ACANS有限差分数值模拟平台开展气动热数值计算，收集用于神经网络训练的气动热数据，该程序气动热计算结果的可靠性已得到相关研究的验证[21-22]。通过数值模拟获得了飞行器在50个飞行状态下的表面热流分布数据作为建立气动热快速预测代理模型的样本数据库。其中，单个飞行状态数值模拟耗时约107 min。飞行状态由飞行高度H、马赫数Ma、攻角α和侧滑角β确定，具体参数见附录A中的表A1。根据交叉验证方法，取其中的前3/4(序号1～38)作为训练集用于神经网络的训练，剩余的1/4(序号39～50)作为测试集用于神经网络的精度评估及超参数调整。

为了建立气动热快速预测代理模型，以数值模拟中表面网格数量为基础，在每个网格节点均建立如图1所示的RBF神经网络。对于图3所示的飞行器数值模拟表面网格节点数量为20 559，则建立相同数量的RBF神经网络，每一个神经网络的输入变量为飞行高度、马赫数、攻角、侧滑角，输出变量为热流、压强。根据1.1和1.2节正则化RBF神经网络的构建方法，网络共分为3层：输入层神经元数d=4，输出层神经元数l=2，隐藏层神经元数量与训练样本数量相同，即q=38。

由于采用了正则化的RBF神经网络，隐藏层神经元基函数的中心向量ch与训练样本的输入向量相同。对于该神经网络唯一的超参数为隐藏层基函数宽度σh，通常采用均匀宽度，一般固定为

(7)

式中：dm为隐藏层所有神经元所选基函数中心之间的最大距离。在以附录A表A1中前38个状态作为模型训练集的条件下，采用式(7)计算所得隐藏层基函数宽度σh为3.2。

2.2 基函数宽度对代理模型预测结果的影响

输入层至隐藏层非线性变换中所采用的基函数为高斯函数，其一般形式为

(8)

对高斯基函数而言，宽度的大小决定了每个基函数对输入的影响范围，宽度越小，表明输入信号的影响范围越小，得到的输出结果越不光滑。另外，当(x-μ)→∞时，有g(x) →0。

图4给出了μ=0、x∈[-400,400]时，高斯基函数随宽度σ的变化情况。从图中可以看出，随着基函数宽度的增加，高斯基函数的作用范围不断变大。对于宽度大的情况，可以通过较少数目的神经元完成所有输出样本空间的映射，因此所需神经元较少；而随着宽度的减小，每一个神经元的作用范围在逐渐变小，因此需要更多的神经元来描述样本空间中的任意输入。因此，宽度选择对预测结果有很大影响。隐藏层径向基函数的宽度由人为给定，现有研究[14]表明基函数宽度将对代理模型精度产生影响。为了分析超参数基函数宽度对代理模型预测结果的影响并确定合适的基函数宽度选取范围，本文除采用式(7)的方法外，还在给定基函数宽度为2、10、20、50、70条件下分别开展模型训练并对基函数宽度对代理模型预测结果的影响开展分析。

图4 不同宽度σ的高斯函数形状Fig.4 Shapes of Gauss function with different σ

从附录A的表A1中选取前38个作为训练集，给定不同的基函数宽度进行模型训练，获得对应的气动热快速预测代理模型。由于采用了正则化径向基神经网络结构，训练耗费时间最多的为通过最小二乘或伪逆法求解隐藏层和输出层之间的权值矩阵，因此训练时间与权值矩阵维度密切相关。本次训练权值矩阵为38×38，训练耗时约41 s。将附录A中表A1的最后12个状态作为测试集(表1)，采用不同基函数宽度的气动热快速预测代理模型对测试集状态进行飞行器表面热流预测，单机串行每个状态耗时约1 s。相比之下，同等网格数量下采用数值模拟方法并且采用并行计算仍需要约107 min，可见所提出的代理模型方法在计算效率上具有巨大的优势，可以快速给出整个飞行走廊内飞行器气动热数据，有效缩短飞行器气动热设计的周期。

表A1 训练集状态参数Table A1 State parmeters of train set

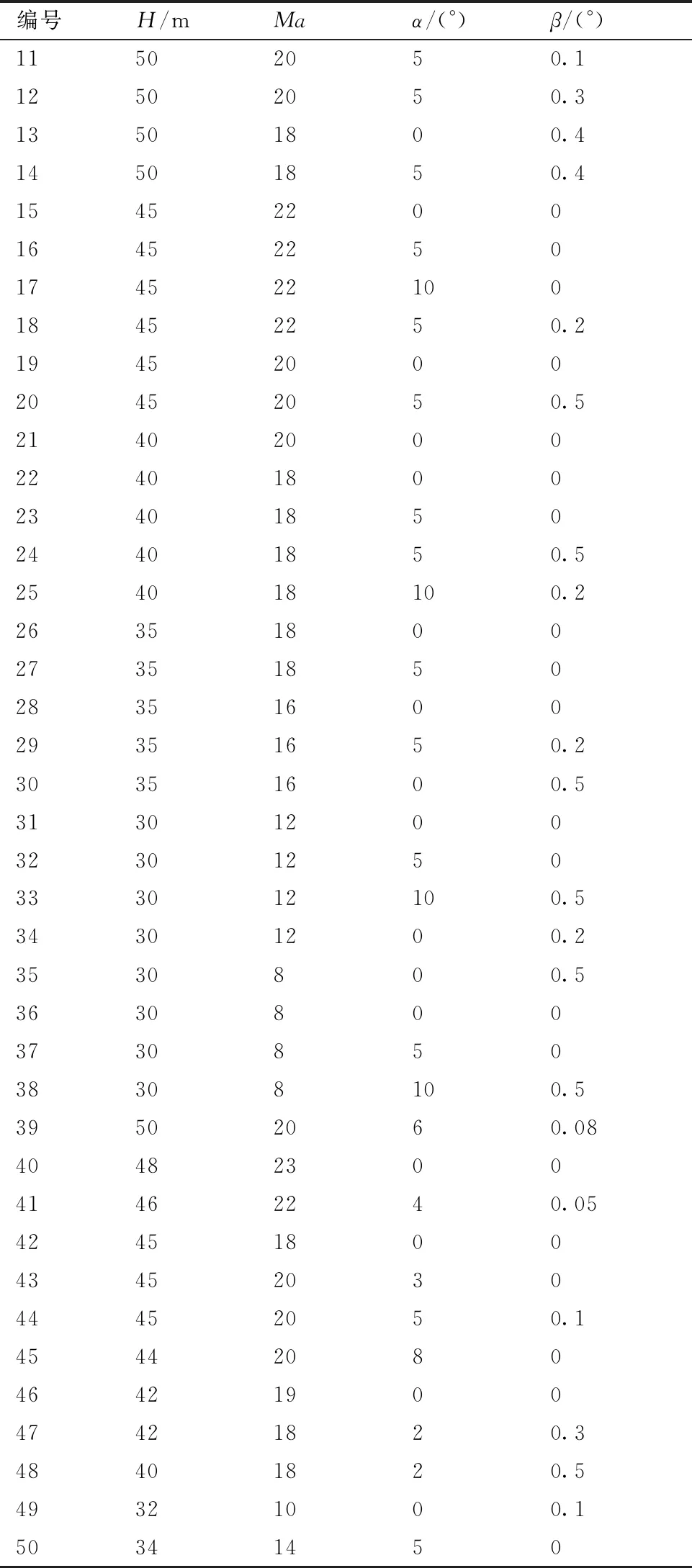
续表

表1 测试集状态参数Table 1 State parmeters of test set

为了分析不同代理模型计算结果的精度，采用飞行器头部驻点热流的整体均方根误差RMSE对代理气动热预测结果进行评估，RMSE计算公式为

(9)

式中：N为测试集检验点个数；yi为数值模拟弹头热流预测结果；y′i为本文所建立的代理模型所预测飞行器表面热流结果。

图5给出了飞行器头部驻点热流的整体均方根误差RMSE随所采用基函数宽度σ的变化曲线。从图中可知，头部热流最大值的整体均方根误差随着基函数宽度σ的增大而减小，并在基函数宽度大于20后呈收敛趋势。一方面，整体均方根RMSE的减小代表着代理模型泛化能力的增强；另一方面，随着基函数宽度的增加，隐藏层至输出层的权值矩阵中非零元素逐渐减少，即实际产生响应的神经元数目变少，这将使得隐藏层至输出层连接权的权值矩阵最大值与最小值之间差异变小，数据之间的相似度不断提高，甚至产生较多的冗余数据，造成矩阵的秩不断减小，产生秩亏的现象，不利于权值矩阵的求解。因此，经综合评估确定适用于高超声速飞行器表面气动热预测代理模型的基函数宽度范围为20～50。

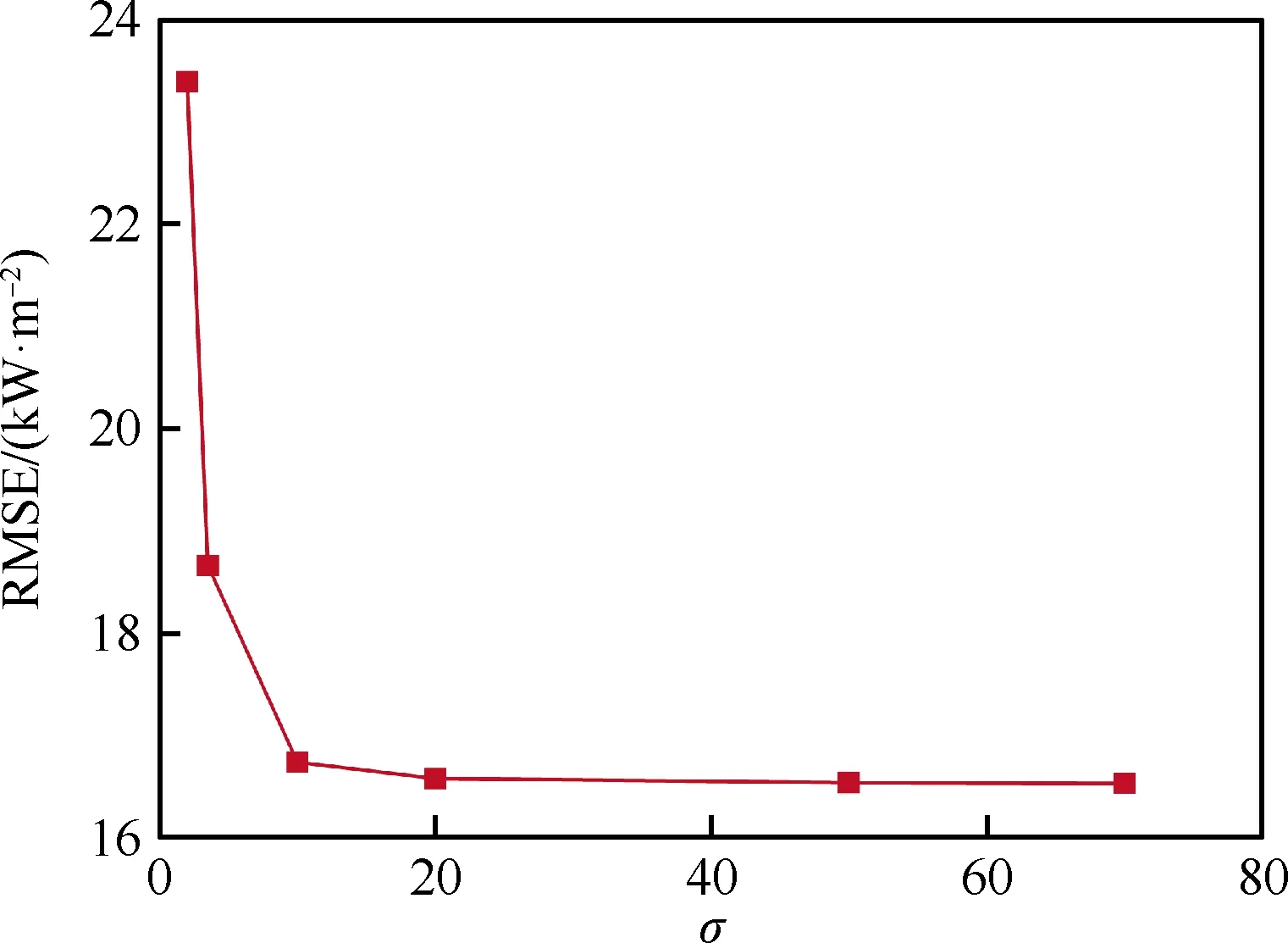
图5 头部驻点热流的RMSE随基函数宽度变化曲线Fig.5 RMSE of stagnation point heat flux on vehicle head with different σ of Gauss function

2.3 代理模型预测结果精度分析

通过2.2的分析，本节选择基函数宽度为50的代理模型预测结果开展进一步的模型精度分析。图6和图7分别给出了表1中序号40和50状态下由代理模型和数值模拟所预测的表面热流(qw)分布云图。从图中可以看出，代理模型所预测热流准确辨识了飞行器头部的高热流区，并且热流分布与数值模拟结果基本一致。

图6 序号40状态代理模型和数值模拟 表面热流云图对比Fig.6 Comparison of surface heat flux contours between ROM and CFD (No.40)

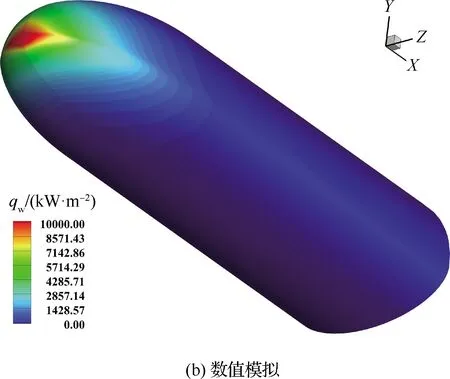
图7 序号50状态代理模型和数值模拟 表面热流云图对比Fig.7 Comparison of surface heat flux contours between ROM and CFD (No.50)

表2给出了代理模型所预测的飞行器头部驻点热流值与数值模拟结果对比。可以看到代理模型在测试集内对于头部驻点热流的预测结果与数值模拟偏差均在10%以内，表明本文所建立的代理模型对头部驻点热流预测具有较高的精度。

对于迎风大面积区域，图8给出了序号40和50状态下迎风面中心线代理模型所预测热流分布与数值模拟结果的对比。从图中可知在迎风大面积区域整体偏差均在10%以内，代理模型也获得了较高精度的预测结果，表明本文所建立的代理模型具有良好的泛化能力。

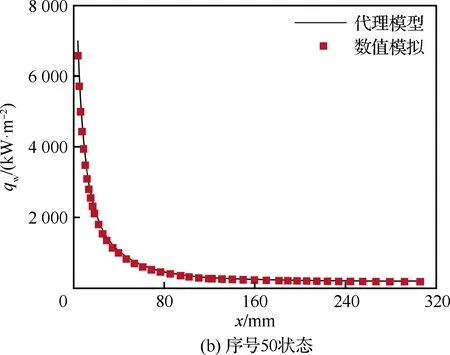
图8 代理模型和数值模拟迎风中心线 热流对比Fig.8 Comparison of heat flux along center line on windward wall between ROM and CFD

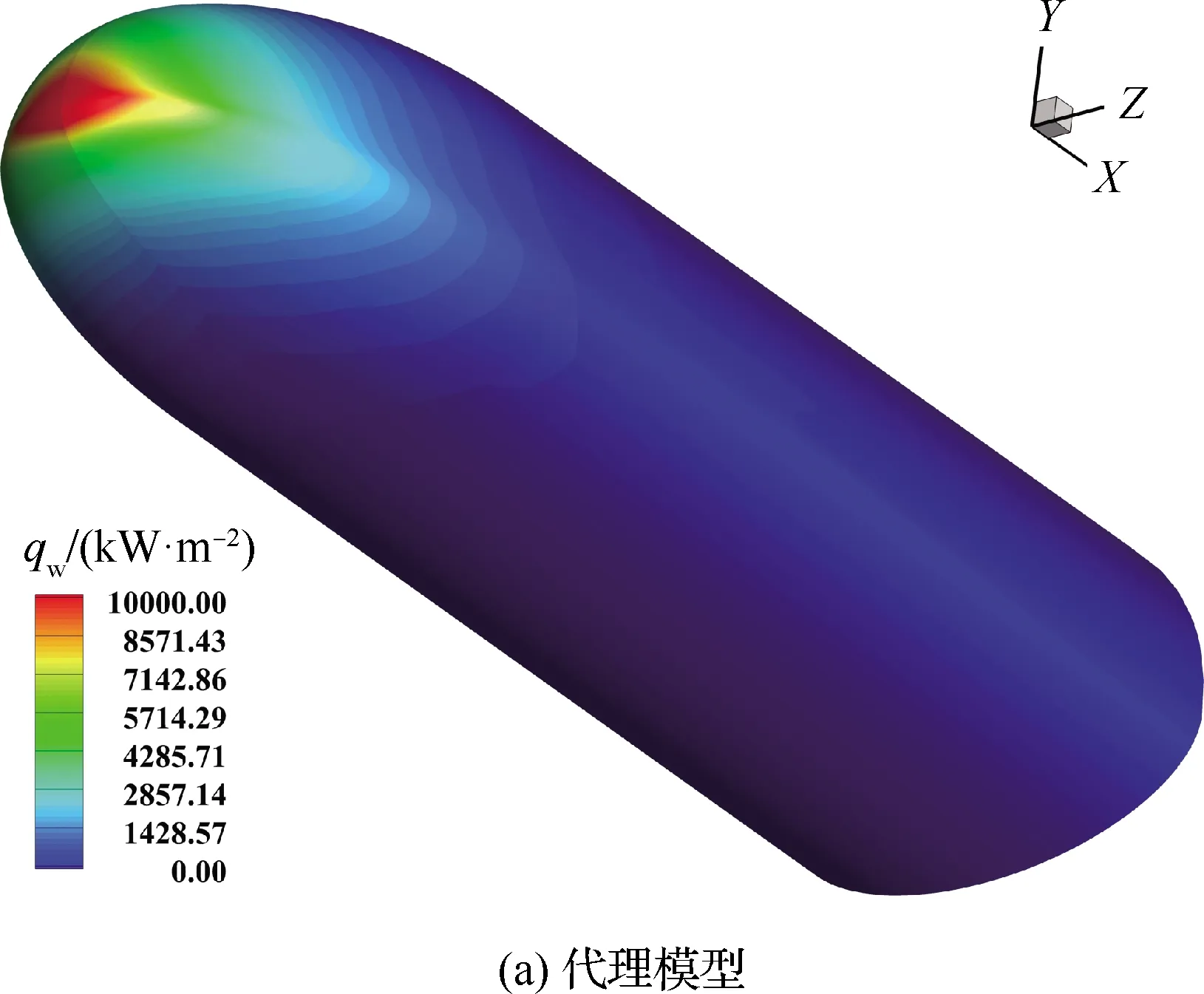
表2 代理模型和数值模拟计算的驻点热流对比

Table 2 Comparison of stagnation point heat

flux between ROM and CFD

序号代理模型/(kW·m-2)数值模拟/(kW·m-2)相对偏差/%391465.931491.661.76402422.922334.573.65412411.932370.71.71421335.641453.848.85431934.671932.610.11441896.231929.331.75452085.572151.773.17461828.901910.814.48471666.711675.900.55481857.621812.822.4149465.18507.629.12501235.731303.535.49

3 结 论

本文基于径向基神经网络发展了一种适用于高超声速飞行器气动热快速预测的代理模型方法，通过美国火星实验室所设计的椭圆钝化高超声速飞行器对该方法进行验证，得到结论如下：

1) 本文所提出的代理模型方法在模型训练完成后能够快速进行飞行器表面热流预测，测试算例中在不考虑建立训练集和神经网络训练时间的前提下，单个飞行状态下使用代理模型计算时间降低至约1 s，而相同条件下利用ACANS程序数值模拟则需要约107 min。代理模型方法在计算效率上具有巨大的优势，可以快速给出整个飞行走廊内飞行器气动热数据，能够有效缩短飞行器气动热设计的周期。

2) 代理模型中基函数宽度将影响飞行器表面热流预测结果的精度。测试集飞行器头部驻点热流整体均方根误差随基函数宽度变化曲线表明，整体均方根误差随着基函数宽度的增大而减小，并在基函数宽度大于20后呈收敛趋势。经综合评估，确定适用于高超声速飞行器表面气动热快速预测代理模型的基函数宽度范围为20～50。

3) 头部驻点热流和迎风中心线上热流分布曲线的代理模型和数值模拟结果对比表明，代理模型在测试集内对于头部驻点和迎风大面积区域热流的预测结果与数值模拟偏差在10%以内，表明本文所建立的代理模型能够获得较高精度的气动热预测结果，并具有良好的泛化能力。