狄拉克δ-函数及有关应用

郑神州， 康秀英

(1. 北京交通大学 理学院，北京 100044; 2. 北京师范大学 物理系， 北京 100875)

狄拉克δ-函数是一类“奇怪”的函数，有广泛应用. 它按照通常古典的函数定义方式是无法做到，实际上它是非通常意义下的“函数”，更准确地称为“广义函数、Schwarz分布函数或泛函”，它是以英国理论物理学家狄拉克名字命名的，在数学和物理中有着独特的地位[1,2]. 狄拉克 δ-函数可以用来描写物理学中一切点量，如：点质量、点电荷、瞬时源等；数学上可以进行微分和积分变换，为处理数学物理问题带来极大的方便. 尤其它在偏微分方程、数学物理方程、傅立叶分析和概率论等领域都离不开这个函数的应用[3-7]，有了狄拉克 δ-函数，傅立叶变换就不受绝对可积条件限制，通常称为广义傅立叶变换.

狄拉克δ-函数具有悠久的历史, 这得从Kronecker δ-函数讲起, Kronecker δ-函数非常简单：

(1)

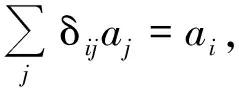
(2)

(简记:(f*δ)(x)=f(x),f(x)δ(x)=f(0)δ(x))

(3)

δ(x-x0)=δ(x0-x)

(4)

从离散过渡到连续，自然地从求和过渡到积分；这看起来两种δ-函数很雷同了. 所以狄拉克δ-函数就达到类似于Kronecker δ-函数的选择器效果，对于δ-函数的选择器作用是泊松先提出的，后来Cauchy利用它的选择器性质研究了许多应用问题，进一步地傅里叶给出了其无穷级数表示，在此基础上狄拉克对研究量子力学时发现了连续型的δ-函数重要作用. 物理上看，狄拉克δ-函数可以看成一些通常意义下函数列的逼近，但严格的数学理论表明：这不是通常意义下的极限(这是泛函意义下的极限，或称“弱收敛”). 事实上，其真正严格意义下的定义方式是在Schwarz分布函数[2](广义函数或泛函)基础上才有的，这表明从此物理上广泛实用的狄拉克 δ-函数可做数学严谨的推理了.

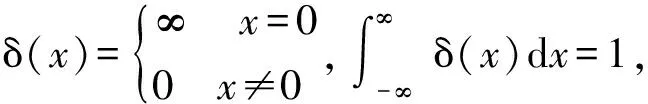
1 狄拉克δ-函数作为广义函数定义

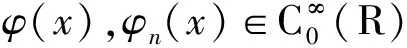
(5)

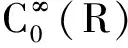
2) 狄拉克δ-函数定义[1,5]

〈δ,φ〉=φ(0), ∀φ∈D(R)

(6)

它是广义函数.事实上:

①δ(x)是线性的：对于任意的α、β∈R以及φ1(x)、φ2(x)∈D(R)，有

〈δ,αφ1+βφ2〉=αφ1(0)+βφ2(0)=α〈δ,φ1〉+β〈δ,φ2〉

(7)

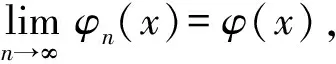
(8)

这里要强调的广义函数收敛性一定要在试验函数作用下收敛的，泛函分析中称为弱收敛.

(9)

简单的验证：这是一个线性连续泛函.任一个局部可积函数按以上做法都有唯一的广义函数与之对应，且可证明：不同的局部可积函数对应于不同的广义函数，并保持线性运算不变；这样可以将局部可积函数f等同于与其对应的广义函数F.反之，狄拉克δ-函数不是通常函数，没有局部可积函数与之对应[1,5].事实上，反证法：若存在这样的局部可积函数f(x), 有

(10)

特别地取特殊的试验函数为

(11)

则φ(nx)∈D(R),且

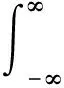
(12)

但另一方面

(13)

这是一个矛盾，所以狄拉克δ-函数没有局部可积函数与之对应.

2 狄拉克δ-函数的逼近方式

上面定义的广义函数有点抽象，下面我们从物理直观上，用各种函数列逼近的方式来理解狄拉克δ-函数，这种逼近也不是通常意义下的极限，而是泛函意义下的逼近，是一种弱形式的极限[1,2,5].

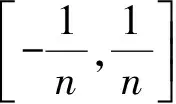
(14)

显然Hn(t)∈Lloc(R)(积分值不超过1).

对任意φ(x)∈D(R)，有

(15)

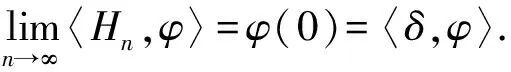
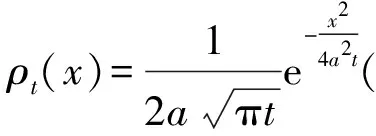
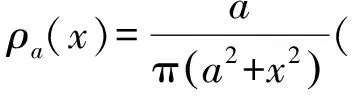
3 广义导数(弱导数)和狄拉克δ-函数

先给出广义导数定义:对一个广义函数f∈D′(R),若存在f′ 使得

〈f′,φ〉=-〈f,φ′〉,∀φ∈D(R)

(16)

则称为广义函数f有一阶广义导数，其广义导数为f′(见文献[1,2,5]).一般地，定义k-阶广义导数为；若有f(k)使得

〈f(k),φ〉=(-1)k〈f,φ(k)〉,∀φ∈D(R)

(17)

称f(k)为广义函数f的k-阶广义导数，k=1,2,….注：通常意义下的导数一定是广义导数，其本质就是分部积分公式；反之不对，从定义得知：广义导数不是逐点定义的.例如：Heaviside函数

(18)

对于任意φ(x)∈D(R)，则有

(19)

所以狄拉克δ-函数可看作是Heaviside函数的广义导数. 考虑函数|x|的第m阶广义导数(m为不小于1自然数)，有

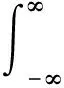
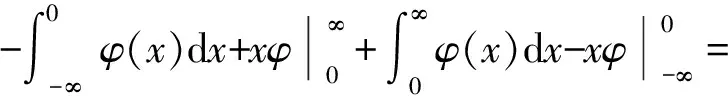
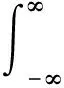
(20)

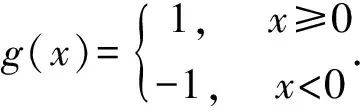
所以|x|′=2H(x)-1.一般地

|x|(m)=2δ(m-1),m≥2

(21)

4 狄拉克δ-函数性质和广义傅里叶变换[1,3,5]

两个已知函数f1(t)、f2(t)卷积定义：

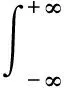
(22)

狄拉克δ(x)函数一些重要性质：

1) 卷积性质

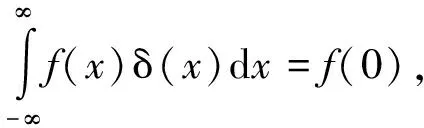
(23)

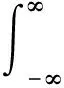
事实上，对于试验函数φ(x)∈D(R)和f(x)的单零点an，由于f(an)=0,f′(an)≠0，在每个an存在邻域都是一一对应，作局部的变量代换y=f(x)

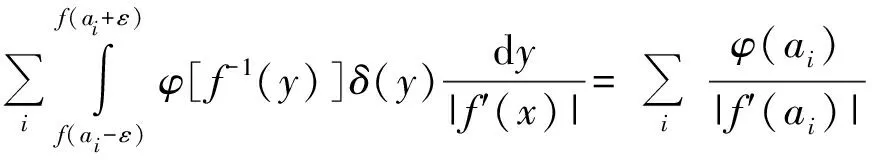
(24)

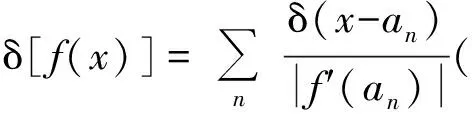
f(x)=(x2-a2)⟹δ(x2-a2)=

(25)

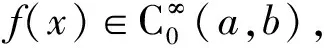
(26)

考虑{φn(x)}是正交基

(27)

得证.

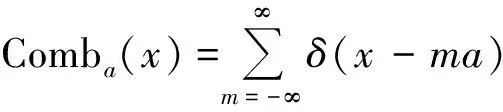
(28)

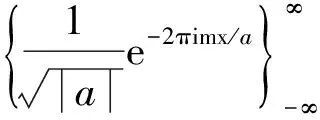
(29)

得证.

5) 三维狄拉克函数：δ(x,y,z)=δ(x)δ(y)δ(z)，即：

类似于一维的性质：

f(x0,y0,z0)， ∀f(x,y,z)∈C(R3)

1)δ(x)函数的傅里叶变换为1,即:F[δ(x)]=1.

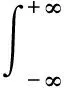
3) 又如求正弦函数f(t)=sinω0t的不是绝对可积的，但它的广义傅里叶变换

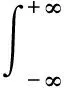
iπδ(ω+ω0)-δ(ω-ω0)

(30)

一般地，不满足可积性条件函数的广义傅里叶变换，其像函数通常与狄拉克δ-函数有关[8].

5 δ-函数在边值问题中的应用

基本解和格林函数是由δ-函数来定义的.这里以拉普拉斯算子为例谈论其在线性偏微分方程中边值问题求解中的应用.

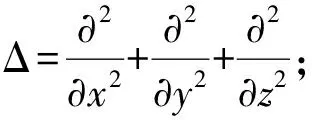
对于任意r∈Ω，有

(31)

其中n为∂Ω上的外单位法向向量.