李导数一种新的讲授方式

何孝凯,曹周键

(1. 湖南第一师范学院 数学与计算科学学院，湖南 长沙 410205; 2. 北京师范大学 天文系，北京 100875)

李导数(Lie derivative)是微分流形上的一类重要导数算子，它是一种对流形M上的张量场沿着某个给定方向求导的运算.李导数在数学和物理中都有广泛的应用[1-8].在我们读到过的教材中，学者们都是先介绍流形上光滑矢量场ξa给出的单参微分同胚群，再介绍流形上的推前映射和拉回映射，然后在此基础上定义流形上的张量场Ta1…akb1…bl沿矢量场ξa的李导数ξTa1…akb1…bl[5-9].唯一不同的是有的教材使用主动语言，有的使用被动语言.主修物理和天文的学生大都没有系统学过微分流形，对推前和拉回映射倍感抽象，对由此诱导的变换也会深感复杂、难懂.所以很多初学者觉得李导数的概念比较抽象，不易掌握.本文将给出一种关于李导数新的讲授方式，该方式摆脱推前和拉回映射，便于初学者理解.

1 矢量场的适配坐标系

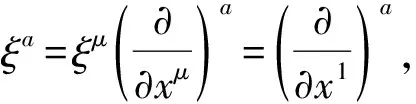
(1)

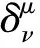
(2)

2 李导数的定义

本节我们将用一种新的方式定义流形上张量场沿某给定矢量场的李导数.这里我们只讨论矢量场的李导数,往其他任意张量场的推广是直接的.设ξa是n维流形M上的一个给定光滑矢量场.对M上的任意光滑矢量场ua，我们定义ua沿ξa的李导数如下

(3)

其中{xμ}(μ=1，2,…,n)是矢量场ξa的适配坐标系，uμ是矢量场ua在适配坐标系{xμ}(μ=1，2,…,n) 坐标基底下的分量.

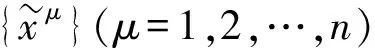
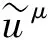
从而

其中第二个等号我们用到了式(2).另一方面，还有性质：

所以有

这就证明了流形上矢量场ua沿给定矢量场ξa的李导数(3)与所使用的适配坐标系无关,所以这个定义是良好的.

3 李导数在任意坐标系下的表达式

上一节我们给出了n维流形上的矢量场ua沿给定矢量场ξa的李导数.根据定义我们可以直接写出在ξa的适配坐标系下李导数的表达式.本节我们将进一步讨论该李导数在任意坐标系下的表达式,进而我们会看到定义式(3)与通常教材中给出的矢量场李导数定义是一致的.

设ξa和ua是n流形M上的两个光滑矢量场， {xμ}(μ=1，2,…,n)是矢量场ξa的适配坐标系，{x′μ}(μ=1，2,…,n)是流形M上的任意一个坐标系(不一定是ξa的适配坐标系).在这两组 坐标系下，ξa和ua可被表示成：

接下来将证明Lξua在坐标系{x′μ}下的表达式为

(4)

为了证明式(4)，首先注意到

(5)

其中第二个等号用到了式(1).于是从式(3)出发，有

(6)

直接计算给出

其中第二个等号用到了式(5).此外

其中倒数第二个等号用到了式(5).从而式(6)可化为

这样就得到了n维流形上的矢量场ua沿给定 矢量场ξa的李导数在任意坐标系下的表达式.当{x′μ}也是矢量场ξa的适配坐标系时，有

从而式(4)化简为

与上一节的定义式一致.

作为本节的结束，讨论定义式(3)与通常教材中定义的李导数的一致性.在通常的教材中，矢量场ua沿给定矢量场ξa的李导数等于矢量场ua和ξa的对易子[5-9]，即

Lξua=[ξ,u]a

(6)

注意到在n维流形M上某坐标{x′μ}系下对易子的表达式为

此等式的右端与式(4)右端一致，可见我们 按定义式(3)引入的矢量场ua沿给定矢量场ξa的李导数满足式(7)，与通常教材中的结果一致.

4 结语

本文中引入了一种新的方式来定义流形上的张量场沿给定矢量场的李导数.首先引入矢量场ξa的适配坐标系概念.实际上适配坐标系的概念并不多余，因为在广义相对论课程中讲授Killing矢量场的时候也会引入适配坐标系的概念,相当于只是把这个概念的讲解提前一点.基于适配坐标系，就可以给出流形上光滑矢量场ua沿ξa的李导数直观定义.同时也很容易可以讲清楚我们的定义与具体适配坐标系的选择无关.在此基础上，进一步给出了矢量场的李导数在任意坐标系下的表达式，与通常教科书讲解的李导数轻松衔接.不同于通常教材从推前映射和拉回映射出发，用映射这一主动观点或者用由映射诱导的无穷小变换这一被动观点来定义李导数[5-10]，我们采用的定义方式更便于初学者理解和掌握.本文中重点讨论了矢量场ua沿ξa的李导数定义，这一做法可自然推广至流形上的任意张量场沿ξa的李导数，在此不再赘述.