气液两相流泵断气过渡过程数值模拟研究
仲高超, 邵春雷
(南京工业大学 机械与动力工程学院, 江苏 南京 211816)
离心泵广泛应用于石油、化工、矿业和农业以及船舶制造业等领域[1-2]。离心泵断气过程是一个复杂的瞬态过程,伴随着气体在短时间内的迅速减少的过程中,其扬程、流量、轴功率等外特性参数也随之发生变化,这个变化过程对泵系统的安全和稳定性的影响也很大。因此,研究断气下时泵内的流体流动情况,对提高泵的安全和稳定至关重要。
近年来,国内外学者对离心泵内的瞬态过程进行了大量的研究[3-5]。吴大转等[6-7]对在不同启动加速度和进口发生空化状态下的快速启动进行了大量的试验研究,发现快速启动过程中的空化会使得泵的性能急剧下降和扬程剧烈波动。Dazin等[8]对4种不同加速启动过程中的瞬态扬程进行了试验研究,发现在瞬态过程中瞬态效应除了与旋转加速度和流动加速度有关,还与泵内部的流场演化结构有关。张玉良等[9]对一台离心泵的不同工况点快速切换过程的瞬态特性进行了数值模拟研究。刘竹青等[10]采用CFX中SST-SAS模型对泵的启动进行了数值模拟,分析了不同启动历时对泵启动瞬态特性的影响,发现随着泵启动历时的减小,会在蜗壳隔舌处产生较大的低频压力脉动。王勇等[11]对一台超低比速离心泵的关阀启动瞬态特性进行了数值模拟,分析了3种不同启动加速度下瞬态和稳定的扬程,发现瞬态比稳态的扬程要高。Hu等[12]对离心泵启动过程的瞬态特性展开了研究,结果表明在叶轮出口压力侧最先出现漩涡,随着时间的推移,旋涡向叶轮中部流道移动,旋涡强度不断增加,当转速、流量等外特性参数到达稳定值时,漩涡强度又开始逐渐减弱。张玉良等[13]建立了一个包含离心泵在内的封闭循环管路系统对停机过程进行了数值模拟,分析了停机过程中的瞬态特性变化和流场中的不稳定流动。周大庆等[14]基于FLUENT数值模拟软件对其进行了用户自定义程序的二次开发,揭示了轴流泵在事故断电中机组转速、流量、转矩与测试点压力等参数随时间的变化规律,以及截面流速场、叶轮叶片压力场的瞬态过程。苟东明等[15]通过采用VOF两相流模型和单相流模型的三维耦合湍流计算方法对水泵水轮机的断电飞逸过渡过程进行了数值模拟,分析了外特性参数随时间的变化规律和不同时刻下流场的演变规律。前人对于泵内瞬态过程的研究大部分集中于泵的启动和停机过程,且其启动时的转速变化规律是可以通过试验测得或者预先给定确定的变化曲线,但是泵在实际的运用中,由于各种原因经常会发生很多不可控的瞬态过渡过程,工作状态的突然变化会导致转速、流量等外特性参数发生剧烈改变,而前人对于泵的突然断气这一方面的数值模拟研究较少。
课题组通过数值模拟方法研究断气后泵内的流动规律,确立了断气过渡过程的判定依据,探讨了气相体积分数和压力随时间的变化规律,通过对比分析了泵的外特性。研究结果对进一步改进泵的结构设计以及提高泵运行的稳定性具有重要意义。
1 流体域的三维模型
课题组所研究的离心泵的额定流量为50 m3/h,额定扬程为80 m,额定转速为2 900 r/min。根据离心泵的结构参数[16],采用Pro/E 5.0三维建模软件对模型泵进行了三维建模,为了减少边界条件对内部流动的影响,对泵的入口和出口处进行了适当的延长。图1所示为流体域的几何模型。
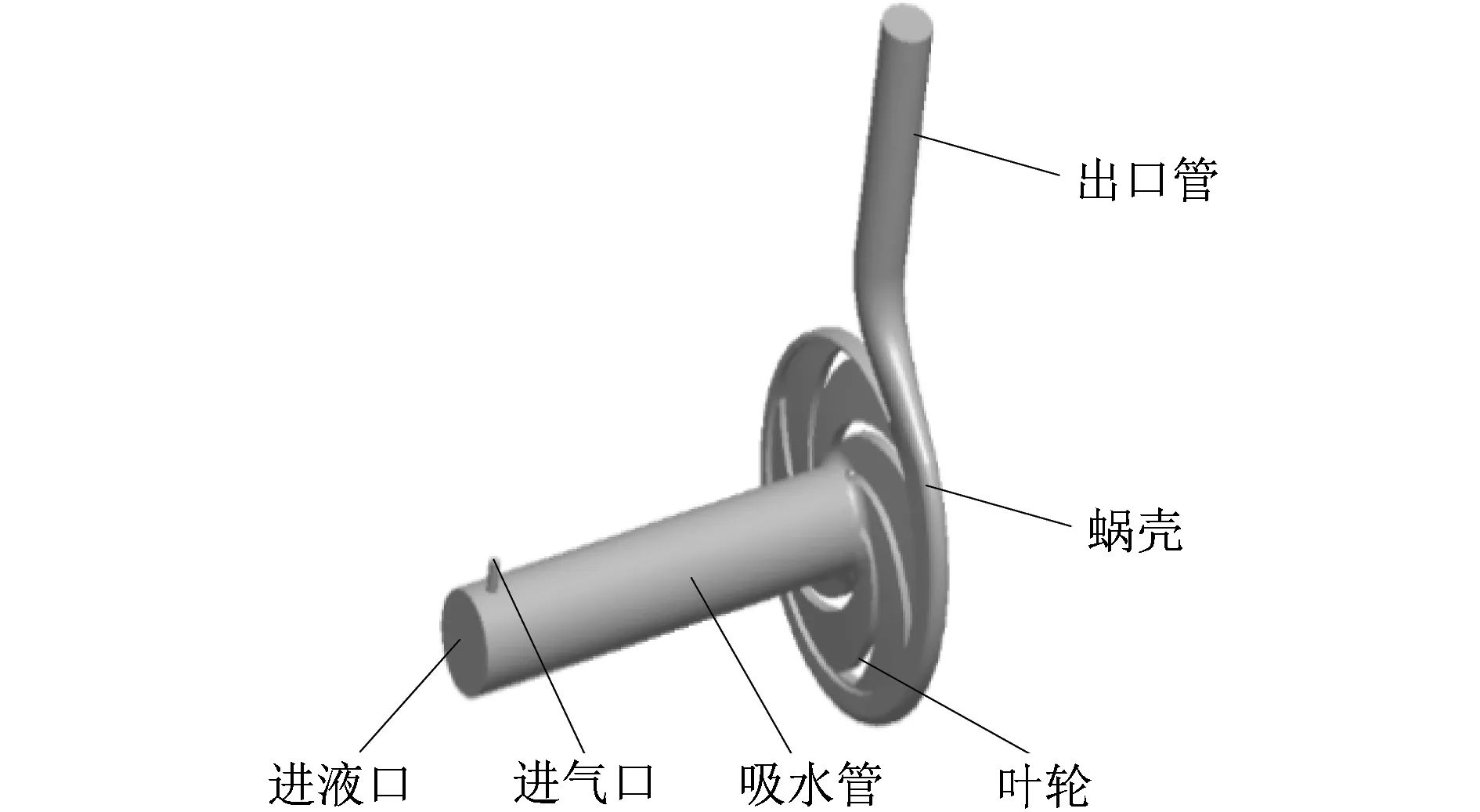
图1 流体域的几何模型Figure 1 Geometric model of pump
2 流体域的网格划分
使用ICEM软件对进口管、吸水管、出口管、叶轮和蜗壳的流动区域进行网格划分,模型计算区域网格如图2所示。叶轮和蜗壳以及进口管区域的网格为四面体,吸水管和出口管部分区域的网格为六面体,对蜗舌和叶片区域的网格进行局部加密处理,加密后网格尺寸为0.8 mm。当网格数从666 514增加到1 448 920,模拟的扬程和效率随网格数的增加略有增加,网格数从1 448 920增加到2 012 537时,泵扬程和效率的波动范围均小于0.4%。因此最终确定几何模型的网格总数为1 448 920,其中进口管和吸水管网格单元数为214 108,叶轮网格单元数为476 161,蜗壳网格单元数为739 651,出口管网格单元数为19 000。
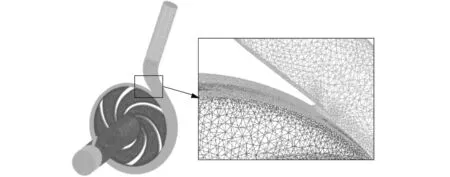
图2 模型计算区域网格Figure 2 Grids of model calculation domain
3 CFD数值模拟
3.1 计算方法
数值模拟中非定常计算采用Eluerian-Eulerian非均相流模型,湍流模型选用SSTκ-ω2方程模型,压力速度耦合采用Phase Coupled SIMPLE算法,气液两相之间的曳力模型仍选用Gidaspow模型,且计算过程中的相关控制方程[17]。
3.2 边界条件
在非定常中液相进口采用速度进口边界条件,进液口的液相流量Ql为50 m3/h,水力直径为80 mm,进气口气相进口也采用速度进口边界条件,进气口的气相流量Qg为40 L/min,水力直径为10 mm,出口采用自由流(outflow)边界条件,壁面采用固壁边界条件。设置转速为2 900 r/min。
3.3 初始条件
非定常计算中的时间步长设置为5.747 1×10-5s,即叶轮旋转1°所需的时间,以进口气相体积分数为4.5%的非定常计算收敛的结果作为初始解,突然改变进口气相体积分数为0,以此进行断气过渡过程的模拟。
4 监测点
为了研究断气过渡过程中的泵内流体流动情况,在泵内关键位置设置了监测点,用于监测这些位置的压力、气相体积分数等参数,从而揭示流动的演化规律。所设置的监测点如图3(a)所示,蜗壳8个截面如图3(b)所示,各监测点的具体坐标见表1。

表1 泵内各监测点位置坐标
表中,Ji表示泵进口表面;Ci表示泵出口表面;J1~J4表示吸水管上的监测点;C1~C4表示出口管中心线上的监测点;m1~m7表示蜗壳第Ⅰ~Ⅷ截面的中心位置监测点;m8-1~m8-9表示蜗壳第VIII截面上的监测点。

图3 泵内各监测点和蜗壳8个截面Figure 3 Location of monitoring points and 8 sections of volute
5 结果讨论
5.1 泵外特性比较
在转速为600 r/min,流量分别为5.0,7.5,10.0,12.5,15.0和18.0 m3/h的工况下对离心泵内部流动进行数值模拟,并预测其外特性。将模拟得到的扬程H-流量Q曲线、效率η-流量Q曲线和功率P-流量Q曲线分别与试验得到的性能曲线进行对比,如图4所示。由图4可知,扬程和效率的模拟值略高于试验值,轴功率的模拟值略低于试验值。这是由于数值模拟中只考虑了泵的水力损失,没有考虑轴承的摩擦损失、叶轮轮盘的摩擦损失和容积损失,而试验中这些损失是无法避免的。

图4 试验与模拟所得泵的性能曲线Figure 4 Performance curves of pump between experiment and simulation
从图4中的数据可得,试验与模拟所得扬程、效率和轴功率的最大相对误差分别为4.1%,3.1%和5.7%,误差在可接受的范围内。上述结果表明,数值模拟可以代替试验准确地预测离心泵的外特性。因此,后续所有研究均采用数值模拟的方法。
5.2 过渡过程判定依据
为了判断气液两相断气过渡过程,对出口C1上的气相体积分数进行了监测,图5所示为泵的出口气相体积分数随时间的变化规律。为便于分析,以切断气源的时刻作为初始时刻(t=0 s)。由图5可知,当t<0.17 s时,泵出口的气相体积分数无明显变化;当0.17 s≤t≤0.60 s时,随着气体量的不断减少,泵的出口气相体积分数不断减少;当t>0.60 s时,泵的出口达到稳定。由图5可以看出,以出口气相体积分数不再发生变化作为断气过渡过程结束的判定依据更为准确。
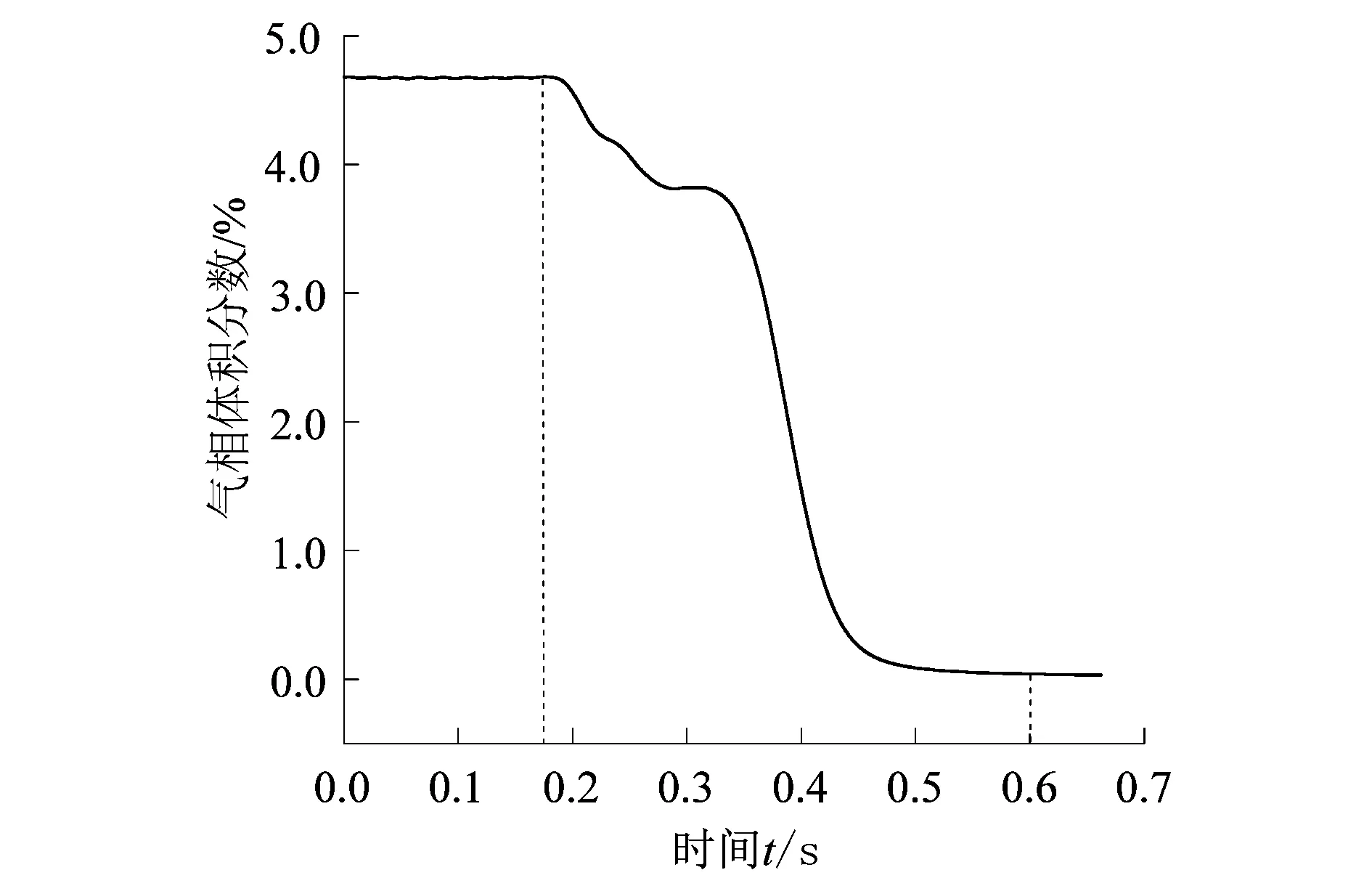
图5 泵出口气相体积分数随时间的变化Figure 5 Variation of gas volume fraction at pump outlet with time
5.3 吸水管内气相体积分数随时间的变化规律
由于气体聚集在吸水管上部,所以在吸水管上部壁面附近设置监测点,各监测点上的气相体积分数随时间的变化规律如图6所示。由图6可知,在靠近吸水管壁面处各监测点上的气相体积分数变化规律大致相同,最初无明显变化,然后逐渐减小,最后趋于稳定。尚未切断气源的情况下,受浮力的作用,沿流动方向,气体逐渐往吸水管上部聚集,使得大部分气体聚集在监测点的上方。因此,靠近叶轮监测点上的气相体积分数比其远离叶轮监测点上的气相体积分数要大。
从图中可以看出,切断气源后,随着时间延长,吸水管内的气体不断减少,各监测点上气相体积分数达到0(即该处无气体存在)的时间也各不相同。当t=0.17 s时,监测点J4上先没有气体,而监测点J3,J2,J1上依次没有气体的时间分别为:0.21,0.23,0.26 s。监测点J4上最先没有气体,而监测点J1上最后没有气体,这是由于沿着流动方向,气体被水逐渐带入叶轮,而后续没有气体流入吸水管内。当吸水管内各个监测点上的气相体积分数都达到0时,吸水管内断气过渡过程结束,所需时间约为0.26 s。

图6 吸水管内气相体积分数随时间的变化Figure 6 Variation of gas volume fraction in suction pipe with time
5.4 蜗壳Ⅰ~Ⅷ截面上气相体积分数随时间的变化规律
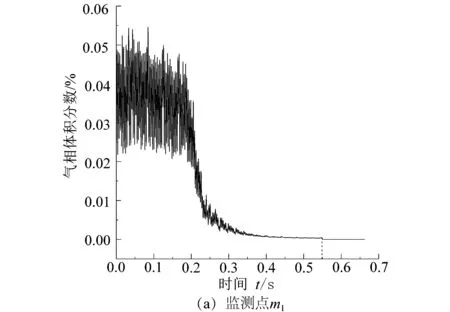
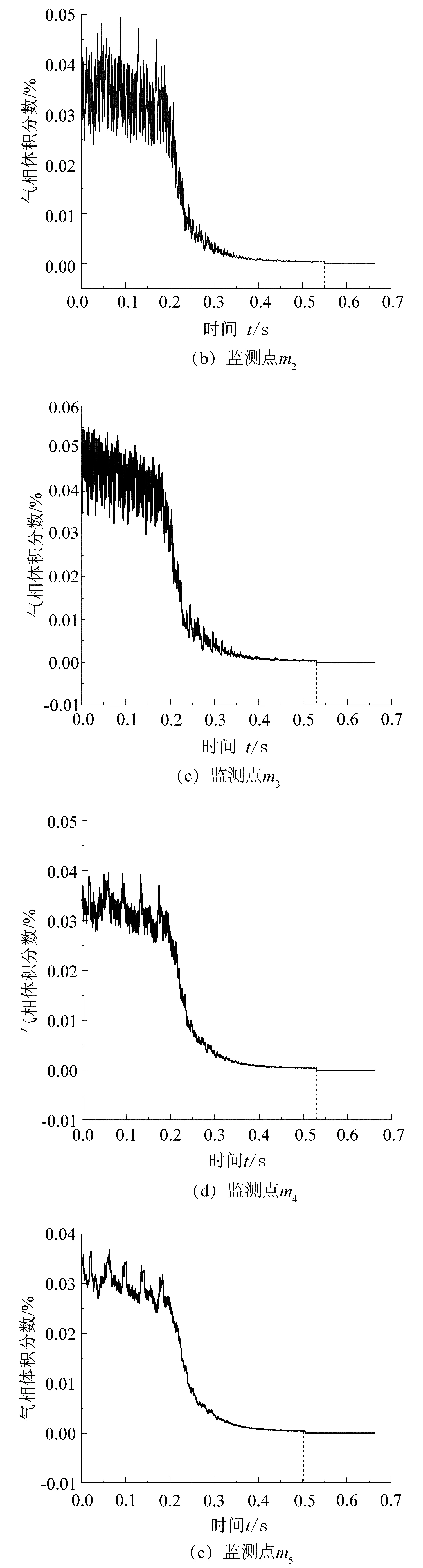
蜗壳Ⅰ~Ⅷ截面上各监测点的气相体积分数随时间的变化规律如图7所示。各监测点上气相体积分数随时间的变化基本一致,先周期波动,再快速减小,最后达到0。由图7可知,虽然监测点m1到监测点m8-5上的变化趋势基本一致,但在尚未切断气源时它们的波动幅值有所不同。监测点m1离蜗舌最近,该处附近的流动较复杂,监测点m1相对于其他监测点上的气相体积分数的波动幅度比较剧烈。由于监测点离蜗舌逐渐增大,受到蜗舌的影响逐渐减小,各监测点的波动幅度逐渐减小,波动逐渐变得平缓。
刚切断气源时,由于蜗壳内还存在气体,各监测点上的气相体积分数呈周期性波动,还未出现下降趋势。在0.55 s之前监测点m1和m2还存在气体,监测点m3和m4在0.53 s之前还存在气体,监测点m5和m6在0.50 s之前还存在气体,而监测点m7和m8-5在0.45 s之前还存在气体。各监测点上气体不存在逐渐消失的时间之所以不同,这是由于沿着流动方向,气体被水逐渐带入泵的出口,而后续没有气体流入蜗壳内,当蜗壳内各个监测点上的气相体积分数都达到0时,蜗壳内断气过渡过程结束,所需时间约为0.55 s。
5.5 蜗壳Ⅰ~Ⅷ截面压力随时间的变化规律
蜗壳Ⅰ~Ⅶ截面内各监测点压力的变化情况如图8所示。由图8(a)可知,刚切断气源泵内还处于气液两相状态,压力先波动一段时间,随着气体含量不断减小,各监测点上的压力逐渐增大,断气过渡过程结束后各监测点上的压力波动呈周期性变化。
图8(b)~(h)是8(a)局部放大图,监测点m1,m2,m3,m4,m5,m6和m7的波动幅度分别为0.190,0.120,0.050,0.045,0.040,0.035和0.025 MPa,不同监测点上压力波动幅度有所不同,监测点m1到m7上的压力波动幅度逐渐减小,这是由于靠近蜗舌附近的流动较复杂,以及越远离叶轮受到叶轮的干扰作用也越小,所以监测点m1上的压力波动相比其他监测点比较剧烈,在蜗壳流道内,随着半径的增大压力逐渐增大。各监测点的压力大小并不相同,从监测点m1到m7压力平均值逐渐增大,也就是说,在蜗壳内沿着流动方向,压力逐渐增大,这与一般离心泵内的压力分布规律是一致的。

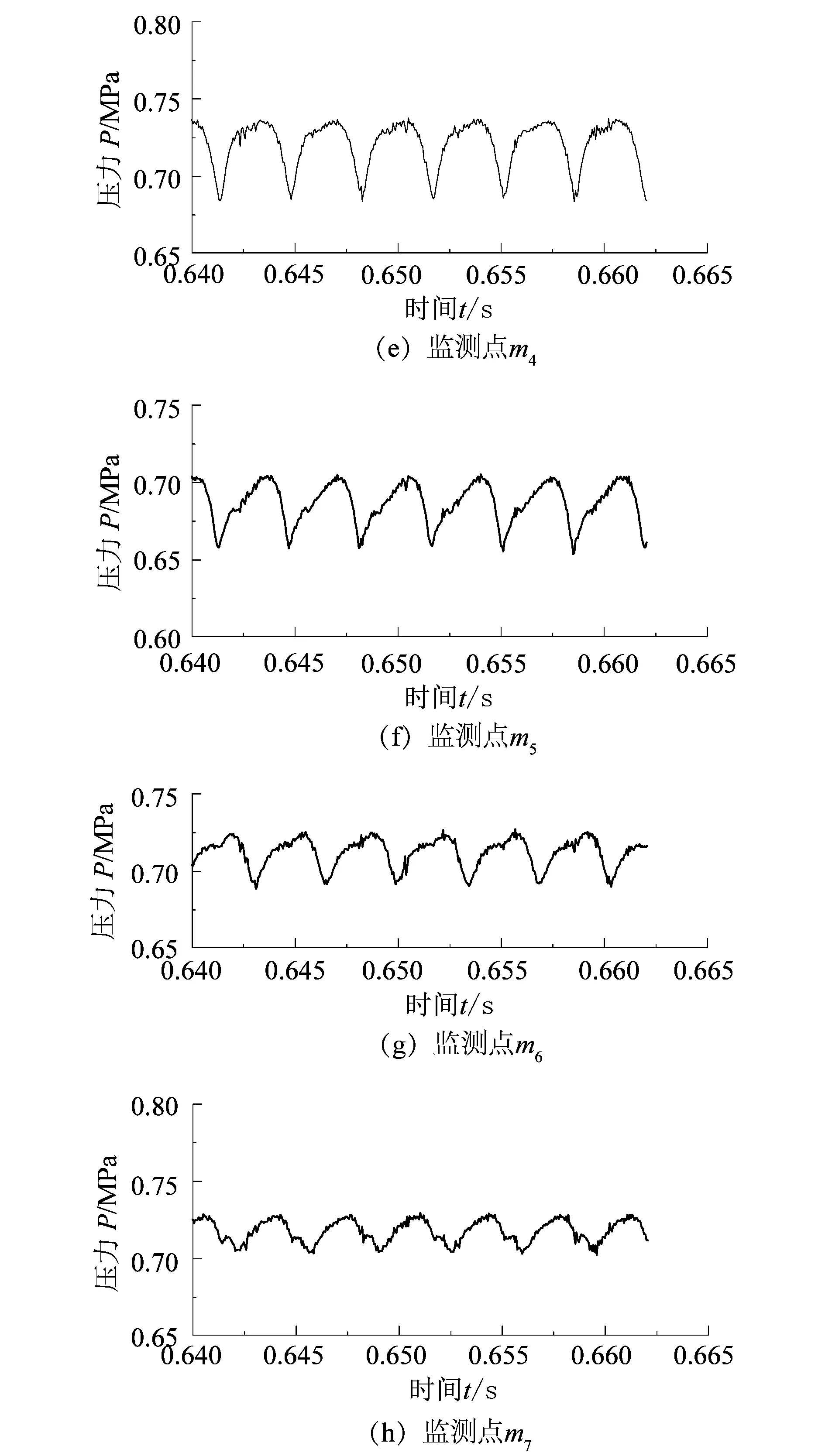
图8 第Ⅰ~Ⅶ截面上压力随时间的变化Figure 8 Variation of pressure on section Ⅰ to Ⅶ with time
蜗壳第Ⅷ截面上各监测点的压力随时间的变化规律如图9所示。由图9可知,沿着蜗壳的径向,监测点m8-1~m8-9上的时均压力逐渐增大,这符合蜗壳内压力的分布规律。沿着蜗壳的径向,监测点m8-1~m8-9上的压力波动幅度和相位均基本相同,表明压力变化具有及时性,这一规律与截面上气相体积分数随时间的变化不同。
6 结论
课题组采用Eulerian-Eulerian非均相流模型和SSTκ-ω湍流模型对泵内气液两相流动断气过渡过程进行了数值模拟,确定了泵内断气过渡过程结束的判定依据,并分析了泵内过渡过程流动规律,所得结论如下:
1) 研究了断气时泵出口气相体积分数随时间的变化规律,结果表明,出口气相体积分数在t>0.60 s后才达到稳定状态,因此,以出口气相体积分数作为断气过渡过程结束的判定依据更为合理。
2) 吸水管监测点的气相体积分数随时间的变化规律基本一致:最初无明显变化,然后逐渐减小,最后达到0;越靠近进气口处,断气过渡过程的时间越短。
3) 在蜗壳Ⅰ~Ⅶ截面上各监测点的气相体积分数时均值随时间的变化规律基本相同:刚切断气源时,无明显变化,然后迅速减小,最后达到0。
4) 在蜗壳第Ⅷ截面监测点上的压力波动幅度和相位均基本相同,表明压力变化具有及时性,这一规律与截面上气相体积分数随时间的变化不同。

