波轮式洗衣机悬挂结构力学特性研究
孙 震, 陈海卫*, 牟秋启, 熊 明, 史亚成
(1.江南大学 机械工程学院, 江苏 无锡 214122; 2.无锡小天鹅电器有限公司, 江苏 无锡 214028)
悬挂结构是波轮式洗衣机的重要组成部件,而吊杆作为悬挂结构中的核心部件,其设计参数影响着洗衣机诸多特性。国内外学者对于悬挂系统的研究,主要集中在理论建模[1-3]和动态特性[4-5]等方面。陈海卫等[6-7]建立了波轮式洗衣机振动模型,分析了悬挂系统广义力,并建立了悬挂系统的空气动力学模型。刘志鹏[8]建立了悬挂系统在变质量大位移情况下的动力学方程。赵平等[9]研究了洗衣机悬挂系统在不同激振频率与激振幅值下的动态响应特性,为悬挂系统设计提供了一些理论依据。张华等[10]建立了波轮洗衣机多体动力学平台,阐述了吊杆的设计方法。但迄今为止,关于洗衣机吊杆悬挂点高度的选择,尚无系统性的讨论分析。课题组通过在MATLAB中建立波轮式洗衣机振动模型,研究了吊杆悬挂点高度对波轮式洗衣机静力学与动力学特性的影响,明确了吊杆悬挂点高度与洗衣机部分关键特性的关系,为深入研究吊杆设计参数准则提供了参考。
1 波轮式洗衣机振动模型
1.1 坐标系的建立
课题组以小天鹅某款波轮式洗衣机为研究对象,该款洗衣机电机采用直驱方式。洗衣机中的液体平衡环会减小洗衣机稳态振幅,但也会增大洗衣机瞬态振幅,本研究主要分析洗衣机本身悬挂结构方面的静力学与动力学特性,暂不考虑液体平衡环的影响。如图1所示,波轮式洗衣机主要由外壳、悬挂模块和工作模块3部分组成。悬挂系统主要由4根吊杆组成,每根吊杆底部都装有弹簧阻尼器。为建立波轮式洗衣机的振动模型,创建如图1所示的2个坐标系:参考系Or-XrYrZr与动系Om-XmYmZm。参考系原点Or固结于大地,Zr轴为洗衣机静止时盛水桶中心轴线;设吊杆下部与盛水桶的悬挂平面为平面A,则动系原点Om位于Zr轴与平面A的交点。动系相对于参考系的姿态用卡尔丹角[αβγ]T描述。
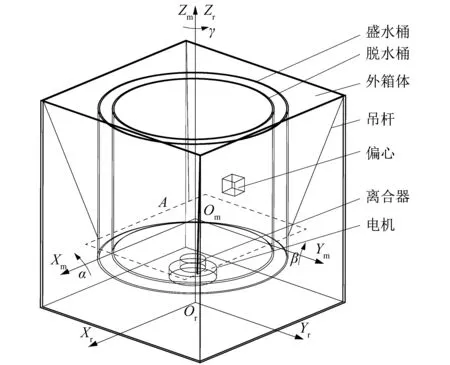
图1 洗衣机结构及坐标系Figure 1 Structure and coordinate system of washing machine
1.2 盛水桶、电机定子与电机支座的动力学描述
盛水桶、电机定子、电机支座与动系Om-XmYmZm固结,以此类刚体质心建立局部坐标系Od-XdYdZd,为方便计算,以及增减刚体数量,可将所有此类刚体叠加为等效刚体1,则其总动能T1可描述为:
(1)
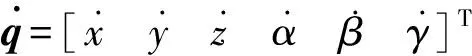
1.3 脱水桶、电机转子与波轮的动力学描述
脱水桶、电机转子与波轮通过旋转轴与动态坐标系连接,可将该类部件叠加为等效刚体2,则其质心在动系下的位置矢量为:
r2=[0 0h2]T。
(2)
式中h2为等效刚体2质心高度。
则等效刚体2的总动能T2可描述为:
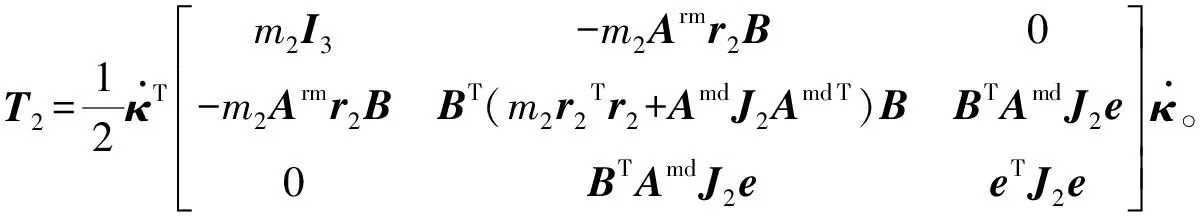
(3)

1.4 衣物偏心的动力学描述
忽略惯量,衣物偏心通过旋转轴与动系连接,其质心在动态坐标系下的矢量位置为:
r3=[R3cosθR3sinθh3]T。
(4)
式中:R3为衣物偏心旋转半径;h3为偏心高度;θ为电机旋转角。
则衣物偏心动能
(5)
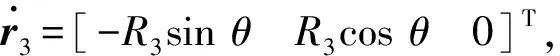
1.5 系统重力势能的描述
将系统内所有部件的重力势能相加,可得系统总的重力势能:
(6)

1.6 广义悬挂力的描述
波轮式洗衣机悬挂系统由4根吊杆组成。吊杆上下端通过球铰分别与外箱体、盛水桶连接。根据文献[11]4根吊杆产生的广义悬挂力
(7)
式中:Qi,rdi,FDi,MDi分别为第i根吊杆的悬挂力、下悬挂点位置矢量、所受力与力偶。
如图2所示,盛水桶近似于圆柱体,悬挂结构垂直于盛水桶外壁;L0为弹簧原长;L1为悬挂点下的套筒与底座长度之和;L2为吊杆下悬挂点距盛水桶外壁距离;H为吊杆下悬挂点距地面高度;φ为吊杆倾斜角;R0为吊杆底座半径;则弹簧压缩极限
(8)
式中μ为弹簧可压缩量与弹簧原长的比值。

图2 吊杆底端悬挂结构Figure 2 Suspension structure at bottom of suspender
1.7 系统整体振动模型
设洗衣机符合直线加速规律,则在洗衣机加速与稳态工作情况下,电机旋转角θ随时间的变化关系分别为:
(9)
式中:a为电机角加速度;τ为加速总时间,τ=Ω/a;Ω为洗衣机稳态转速。
将式(1),(3),(5),(6)和(7)代入第二类Lagrange方程,并去除θ自由度上的描述,得系统总振动方程:
(10)

2 洗涤状态下悬挂点高度对系统静力学特性的影响
2.1 系统静力学模型参数
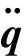
(11)
式中:q*为系统静平衡位置广义坐标,其求解可采用Newton-Raphson迭代法:
(12)
式中:
(13)
式中:fg为系统重力势能Vg对广义坐标q偏导数。
基于上述理论,在MATLAB中建立仿真模型,模型各类基本参数设置如表1所示。

表1 模型基本参数设置
2.2 H对系统静力学特性的影响
在波轮式洗衣机盛水桶下方,通常装有电机、离合器、排水阀等部件,且这些部件需与地面保持一定的安全距离,以避免在工作过程中这些部件与地面相撞。本研究中洗衣机吊杆下悬挂点高度H起始最小值设为0.20 m。
洗衣机负载包括衣物与洗涤用水,为对比不同质量负载对洗衣机静力学特性的影响,设负载总质量分别为0,10和20 kg,且忽略负载产生的偏心。如图3(a)所示,吊杆倾斜角随H的增大而快速增大,不同质量的负载会使吊杆倾斜角略微增大。如图3(b)所示,吊杆弹簧伸缩量随H的增大而增大,且不同质量的衣物负载对弹簧伸缩量的影响是非线性的。弹簧压缩量的增大,对弹簧寿命也会造成不利影响,进而影响洗衣机悬挂系统的使用寿命。如图3(c)所示,吊杆弹簧压缩极限(公式(8))随H的增大而快速下降,其与20 kg负载质量下的弹簧压缩量在0.35 m处相交,如继续增大H,弹簧压缩量将超出弹簧压缩极限。由此可得,在洗涤状态下,吊杆下悬挂点距盛水桶外壁距离不变,且洗衣机最大负载质量为20 kg时,该款机型吊杆下悬挂点高度H最大值应小于0.35 m。
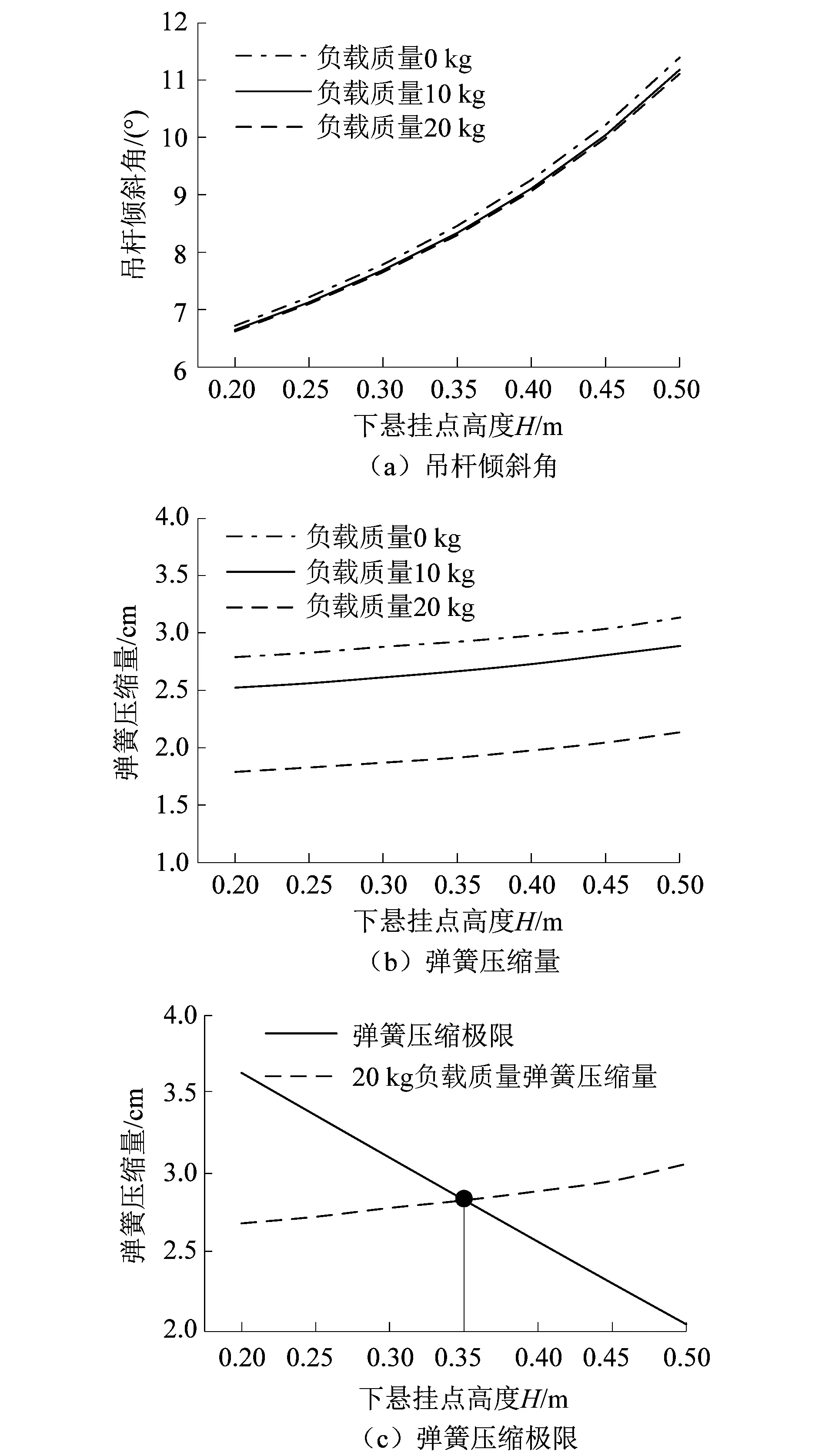
图3 H对静力学特性的影响Figure 3 Influence of H on static characteristics
3 脱水状态下悬挂点高度对系统动力学特性的影响
3.1 系统动力学模型参数
洗衣机处于脱水状态时,转速高且负载质量轻,其动力学特性应是分析重点。设洗衣机稳态转速Ω为600 r/min,角加速度a为5 rad/s2,衣物偏心质量m3为1 kg,偏心高度h3为0.12 m,旋转半径R3为0.21 m,其余模型基本参数参照表1设置。模型仿真过程中,稳态振幅是指洗衣机转速达到稳态转速后测得的振幅。
3.2 H对系统稳态振幅的影响
为直观反映洗衣机盛水桶在脱水过程中的振动情况,故在洗衣机盛水桶外壁上选取了2个测量点:上方测点M与下方测点N。上、下方测量点均位于参考坐标系X轴与盛水桶外测交点,2点高低分布。如图4(a)所示,为避免悬挂结构先与洗衣机机壳碰撞,结构尺寸应满足:
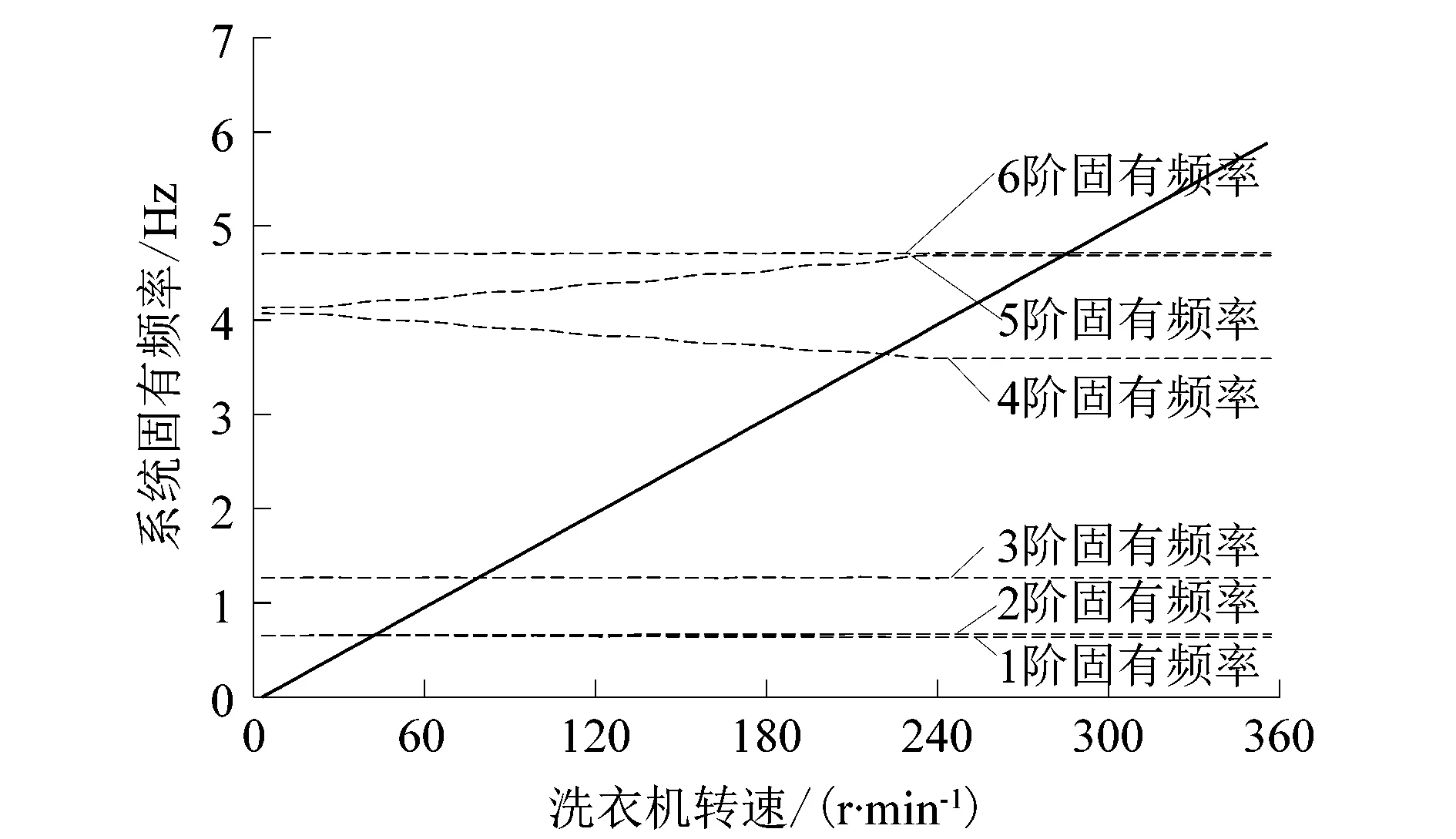
L3 (14) 式中:L3为悬挂结构距洗衣机中轴线的径向尺寸;R1为盛水桶外壁半径。 为保证洗衣机在稳态转速下工作不撞桶,其结构尺寸应满足: Am (15) 式中:Am为盛水桶在稳态转速下的最大振幅;L4为盛水桶外侧与机壳间距,即为盛水桶稳态振幅极限值。 如图4(b)所示,盛水桶上方测点M与下方测点N的稳态振幅,随下悬挂点高度H的升高缓慢下降。当高度H>0.28 m后,点M与N的稳态振幅均处于振幅极限值范围内。由此可得,在脱水状态下,最大偏心质量m3为1 kg,偏心高度h3为0.12 m,旋转半径R3为0.21 m,稳态转速为600 r/min时,该款机型吊杆下悬挂点高度H最小值应大于0.28 m。 图4 悬挂结构与H对系统稳态振幅的影响Figure 4 Suspension structure and influence of H on steady state amplitude of system 为了研究波轮式洗衣机吊杆下悬挂点高度H与洗衣机系统临界频率之间的关系,将式(10)整理化简为: (16) 式中:C为系统总阻尼矩阵;G为陀螺矩阵;K为系统刚度矩阵;f为系统广义力;n为洗衣机实时转速。 在吊杆下悬挂点高度H为0.35 m时,洗衣机系统自身的坎贝尔图如图5所示。图5中虚线自下而上分别为系统在各转速下的前6阶固有频率,过原点的实线为洗衣机转速对应的固有频率,实线与虚线的6个交点即为系统前6阶临界频率。 图5 H=0.35 m洗衣机系统坎贝尔图Figure 5 Campbell diagram of washing machine system at H=0.35 m 表2所示为不同吊杆下悬挂点高度情况下,洗衣机系统的前6阶临界频率。分析可以发现,洗衣机前3阶临界频率随高度H增大而逐渐增大,后3阶临界频率随高度H的增大而逐渐减小。洗衣机前6阶临界频率总趋势是随高度H的增加而趋于集中。系统临界频率过于集中,更易造成共振现象,所以在仅考虑系统临界频率时,吊杆的下悬挂点高度H应取较小值。 表2 不同H下的系统临界频率 课题组通过建立的波轮式洗衣机振动模型,分析了洗衣机吊杆下悬挂点高度H,对不同工作状态下洗衣机力学特性的影响,得出以下结论: 1) 在洗涤状态下,下悬挂点高度H增大将引起吊杆倾斜角、弹簧压缩量的增大,同时降低弹簧压缩极限。针对此状态下的静力学分析,可确定下悬挂点高度H的最大值。 2) 在脱水状态下,下悬挂点高度H增大使得临界频率趋于集中,而洗衣机稳态振幅呈减小趋势。针对此状态下的动力学分析,可确定下悬挂点高度H的最小值。 3) 综合考虑,下悬挂点高度H的选取是一项系统性工程:既要保证洗涤状态下,吊杆弹簧压缩量不超过弹簧压缩极限,从而满足静力学要求;又要保证脱水状态下,洗衣机稳态转速下的最大振幅不超过振幅极限值,从而满足动力学要求,并最终确定满足设计要求的下悬挂点高度H。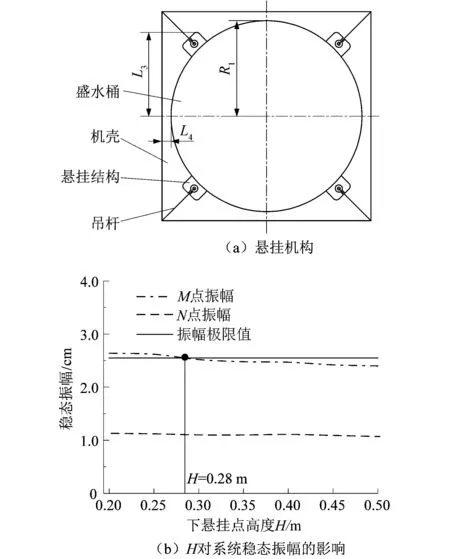
3.3 H对系统临界频率的影响

4 结论

