基于STIRPAT模型的临沂市工业碳排放分析及预测

吴彤，张兴宇，程星星，孙荣峰，王志强，耿文广，王鲁元*，冯太

（1.齐鲁工业大学（山东省科学院）能源研究所，济南250014；2.山东大学能源与动力工程学院，济南250001；3.山东科技大学机械电子工程学院，山东青岛266590）

0 引言

作为全球最大的发展中国家和碳排放大国，我国在第75届联合国大会上提出了“二氧化碳排放力争于2030 年前达到峰值，努力争取2060 年前实现碳中和”的目标。当前，我国碳排放仍然处在“总量高、增量高”的历史阶段，超过85%的碳排放来自能源活动。2020 年年末，我国非化石能源占比约为15%，化石能源占比依然很高。为实现碳达峰、碳中和，“十四五”期间需要加快推动能源革命，建设清洁低碳、安全高效的能源体系，提高能源供给保障能力。这是一场广泛而深刻的经济社会系统性变革，是一场挑战，更是一场硬仗。

山东省作为我国的工业大省之一，碳排放量一直处于全国前列，据《山东省统计年鉴》数据，2020年原煤产量高达10 922.0 万t，焦炭产量为3 162.6万t，2020 年生产总值为73 129 亿元，比上年增长了3.6%，第二产业结构从39.9%下调到39.1%。因此，在保证稳定国内生产总值（GDP）增长的前提下，加大节能减排力度是山东省近几年来的首要任务。目前，针对国内碳排放预测的研究相对较少，且多数集中在全国或大规模区域范围，鲜有地方性的碳排放预测模型。而对省、市级区域进行碳排放数据的预测是实现全国碳达峰工作的重要前提。为使省、市级区域更好地实施碳减排，本文以山东省临沂市为例，根据2009 —2019 年临沂市工业碳排放数据建立相关模型，分析影响碳排放量的相关因素，预测2020—2030 年的碳排放发展趋势，并根据预测结果为节能减排工作提出相应的建议。

1 文献综述

目前常用的碳排放预测模型有可拓展的随机性环境影响评估（STIRPAT）模型、中国能源政策综合评价（IPAC）模型、环境库兹涅茨曲线（EKC）预测模型、灰色预测模型（GM）（1，1）、反向传播（BP）神经网络、对数平均迪氏指数（LMDI）模型等。国内外许多学者采用各种方法进行了深入的研究。姜克隽等［1］运用IPAC 模型对我国长期温室气体的排放进行了预测研究，通过假设基准、低碳、强化低碳场景及其主要参数，预测我国化石燃料排放的碳在低碳环境下将于2030 年实现碳达峰。佟昕等［2］运用STIRPAT 模型较全面地对我国2000 —2011 年碳排放的影响因素进行了分析，并运用GM（1，1）对我国2012—2020年的碳排放量进行了预测，但没有考虑我国政策的实时调整，即没有对影响碳排放的各个因素进行定量预测，只是单纯针对因变量进行了预测，无法预知出现碳达峰的时间。渠慎宁等［3］通过STIRPAT 模型对未来我国碳排放峰值进行了预测，其结合全国30 个省份的数据，建立了比较系统的STIRPAT 模型，通过对未来碳排放影响因素的定量预测，得到我国将在2020 —2045 年实现碳达峰的结论。许化等［4］运动EKC模型建立了陕西省碳排放量与人均GDP 的研究模型，在此基础上加入其他3个影响因素对模型进行再检验，最后预测出陕西省经济增长与碳排放量呈现倒“N”型，碳排放量预计在2024 年出现拐点。颜伟等［5］采用SIIRPAT 模型，并通过岭回归的方法预测了山东半岛蓝色经济区碳排放量，结合山东半岛的发展态势确定中增长-低减排模式是最佳发展模式。

不少学者专门在工业碳排放方面进行了研究。韩媛媛等［6］运用STIRPAT 模型对长沙市规模以上的工业碳排放进行了预测，张巍［7］通过STIRPAT 模型对陕西省工业碳排放量进行了预测，这2 项研究均是以工业规模、用工人数、能源强度和能源结构为自变量进行研究。吉林大学解品磊［8］对工业各部门进行细分，应用长期能源替代规划系统（LEAP）模型分别对各部门进行了详细预测，提出了具体可行的措施；郭晓芳［9］利用STIRPAT 模型对遵义市规模以上工业企业碳排放进行了分析，根据影响因子定量分析了各自变量的影响；王海静等［10］通过LMDI 模型分析出影响贵州省电力碳排放的因素，并通过情景假设对未来10年的电力碳排放进行了预测；王莉叶等［11］基于LMDI 模型分析出兰州市主要能源碳排放量的影响因素并进行了情景分析；刘晓燕等［12］对江苏省工业能源消费带来的二氧化碳排放量进行了预测；田泽等［13］就扬子江城市群工业碳排放与经济增长水平之间的关系进行了分析研究；马艳梅等［14］运用探索性空间数据分析（ESDA）方法和STIRPAT 框架下的空间计量模型的分析结果，对山东省工业碳减排提出了相应建议；邓光耀等［15］根据能源消耗的相关数据，对碳排放进行了分解研究，系统核算了各行业能源消费碳排放量。

本文在以上学者的研究基础上，运用STIRPAT模型建立临沂市工业碳排放量与各自变量的关系模型，通过岭回归消除共线性问题，并定量分析各因素的影响程度，通过各自变量的参数估计进行情景假设，分6 种情景模式对临沂市未来10 年工业碳排放进行预测。

2 临沂市工业碳排放影响因素

2.1 STIRPAT模型的建立

STIRPAT 模型是由IPAT 模型拓展而来的［16］，它比后者更灵活，可以引入多个独立变量

式中：I为环境压力；a为模型系数；b，c，d分别为人口、财产、技术水平的弹性系数；e为模型误差；P为人口数量；A为人均财富量；T为技术水平。

STIRPAT 模型在碳排放预测方面的应用往往是将P，A，T这3个变量进行分解或改进。本文的研究对象为临沂市工业碳排放，因此人口规模相应改为工业规模，即工业固定资产Q；财产用人均工业产值U表示；结合临沂市钢铁产业情况，将技术水平分解为能源强度O和能源结构S，其中能源强度O用单位工业产值的综合能耗表示，能源结构S又分为原煤占总燃料的消耗比M和净购入电力N。6 个变量的情况说明见表1。

表1 STIRPAT模型中各变量说明Tab.1 Description of variables in STIRPAT model

模型关系为

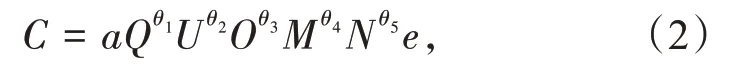
等式两边同时取对数，得到

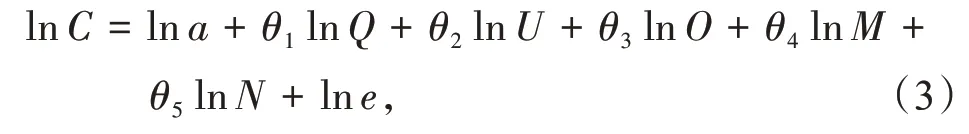
式中：θ1，θ2，θ3，θ4，θ5为各自变量的弹性系数，表示各自变量每变化1%会引起C的θ1%，θ2%，θ3%，θ4%，θ5%变化。

2.2 数据来源及碳排放计算方法

根据《临沂市年度统计年鉴》《临沂市统计公报》数据，查得2009 —2019 年的碳排放量、工业企业的固有资产、年工业生产增加值、人均工业产值、综合能耗、原煤占能源消耗比、工业生产净购入电力等数据。为方便数据采集：年工业生产增加值按2019 年的价格指标取；在岗职工人数按年度平均用工人数；工业净购入电力取工业企业净消耗电力，按实际统计单位万kW·h 计算，其中1 万kW·h=10 MW·h；年度工业生产增加值按工业年度生产总值占年度生产总值的份额计算，其中2017 —2019 年没有给出具体碳排放量，按碳排放量等于2.6 倍的综合能耗推算。

本文研究对象为临沂市工业企业，根据《2019年碳排放补充数据核算报告》，其工业碳排放主要由化石燃料燃烧排放、工业生产过程排放、净购入电力热力排放、固碳产品隐含排放4部分组成［17］

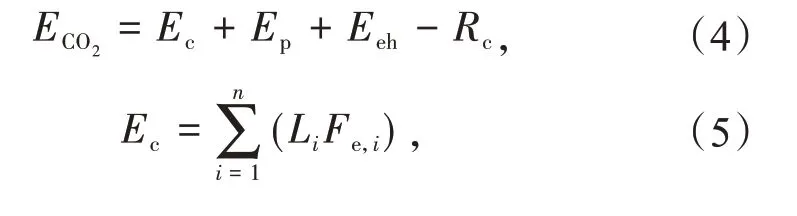
式中：ECO2为工业生产活动产生的所有碳排放量；Ec为企业所有净消耗的化石燃料燃烧产生的碳排放量；Ep为工业生产过程中产生的碳排放量；Eeh为净购入电力热力附加的碳排放量；Rc为固碳产品隐含的碳排放量；Li为内第i种化石燃料的活动水平，GJ；Fe，i为第i种化石燃料的碳排放因子（以CO2计），t/GJ；i为净消耗化石燃料类型。

化石燃料的活动水平按下式计算

式中：Qdw，i为第i种化石燃料的平均低位发热值，固体或液体燃料单位为GJ/t，气体燃料单位为GJ/m3；Ci为第i种化石燃料的净消耗量，固体或液体燃料单位为t，气体燃料单位为m3。

化石燃料的碳排放因子为

式中：Cc，i为第i种化石燃料的单位热值含碳量（以C计），t/GJ；Of，i为第i种化石燃料的碳氧化率，%。

化石燃料以原煤（以烟煤为主）、天然气、液化石油气、柴油、汽油为主。

2.3 数据处理及结果分析

将整理好的11组数据先进行对数化处理，然后以lnC为因变量，以lnQ，lnU，lnO，lnM，lnN为自变量，通过SPSS软件进行多元线性回归并进行共线性检验，检验结果见表2—4，表中：R为拟合优度。

表2 模型汇总Tab.2 Summary of models

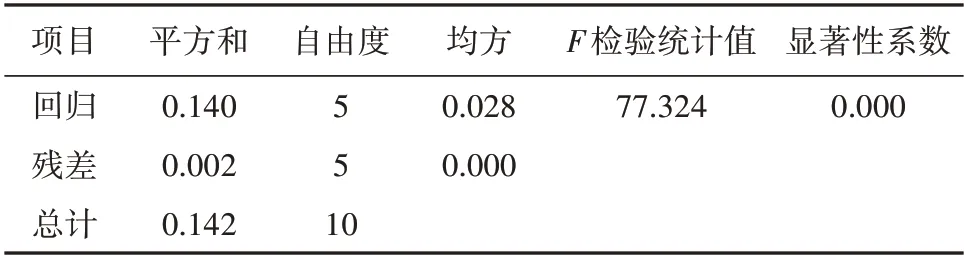
表3 方差分析Tab.3 ANOVA

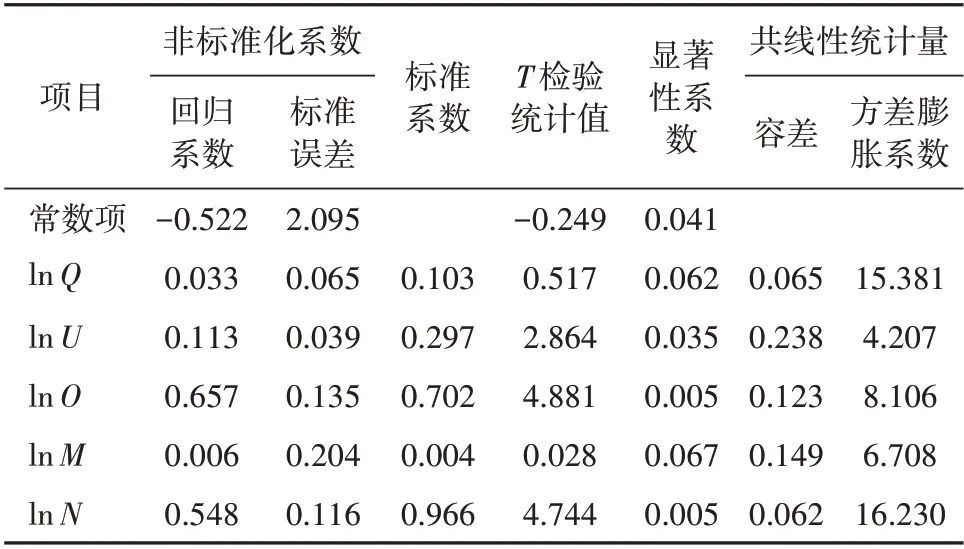
表4 模型系数Tab.4 Model coefficients

分析表中数据可知：R2为0.987，F值为77.324，显著性系数为0，所以方程回归效果显著；自变量和常数项通过了10%的显著性水平检验，回归效果基本满意；但变量lnQ，lnN的方差膨胀系数（VIF）均大于10，其余3 个变量的VIF 值在4～10 之间，因此可以判断5 个自变量之间存在多重共线性问题，需要进行消重。

本文通过SPSS 软件，运用岭回归方法进行消重，岭回归拟合结果如图1 所示，图中：K为惩罚系数。

图1 岭回归系数与K值的关系Fig.1 Relationship between the ridge regression coefficient and K value

从图2 可看出，K值与R²成负相关，即K值越小R²越大，但K值的选取还应通过图1 来确定，只有选取图1 中岭回归系统趋于稳定时的K值，模型的拟合效果才最佳。选取K=0.3 进行岭回归，得到的具体结果见表5—6。

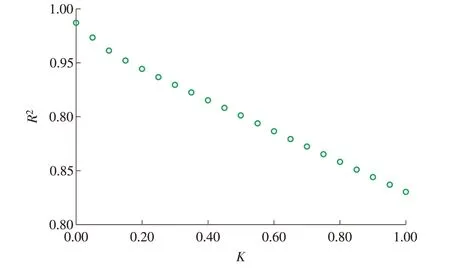
图2 岭回归R²与K值的关系Fig.2 Relationship between the ridge regression R2 and K value

表5 岭回归模型汇总Tab.5 Summary of the ridge regression model

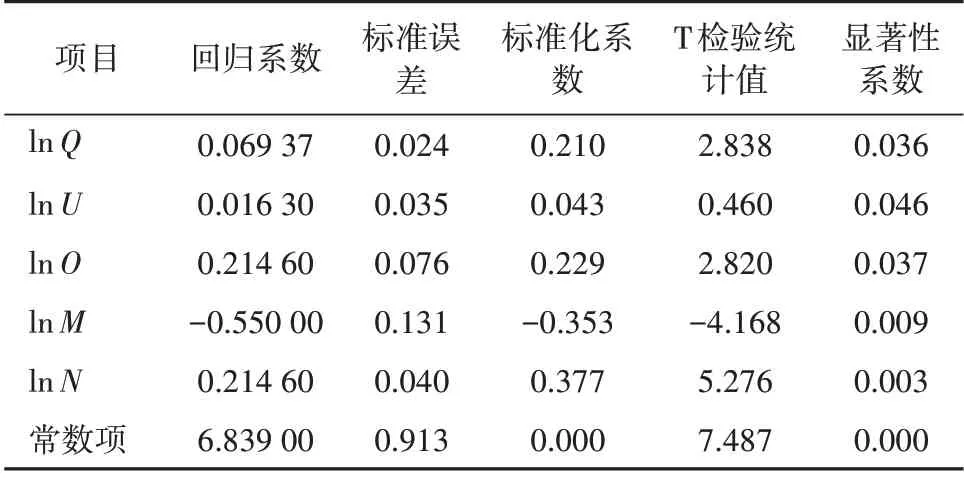
表6 岭回归模型系数Tab.6 Coefficients of the ridge regression model

从拟合结果看，R²为0.930，F值为13.200，显著性系数为0.006，5 个自变量均通过了5%的显著性水平检验，因此模型回归效果良好。

从而可以得到岭回归方程

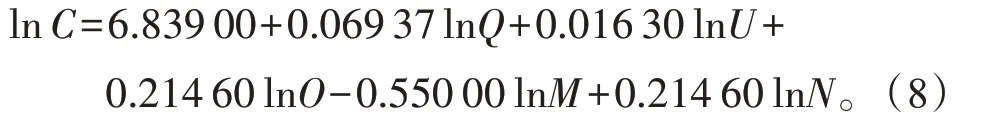
从方程系数看，企业规模（用企业固定资产表示）、人均工业生产增加值、能源强度和工业净购入电力都对工业碳排放量起促进作用，其中工业净购入电力和能源强度每增加1%，工业碳排放量将增加0.214 60%，表明电力的过度使用和能源强度加大将直接导致碳排放量增加。企业固定资产每增加1%，工业碳排放量将增加0.069 37%，人均工业产值增加1%，工业碳排放量将增加0.016 30%，因此以目前来看，工业产值的增加是以增加碳排放为代价的。而增加原煤占能源的消耗比可以抑制工业碳排放量，原煤占能源的消耗比每增加1%，工业碳排放量将减少0.550 00%。通过STIRPAT 模型可以总结出，减少碳排放量可以通过平衡好经济增长与减排的关系和调整能源消费结构。

3 情景预测及结果分析

3.1 预测模型

通过上文的STIRPAT 模型，将公式（7）改写为

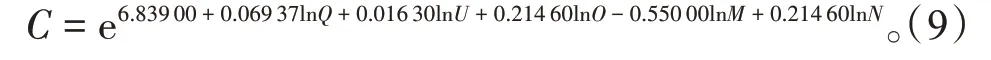
将2009 —2019 年的碳排放数据代入上式，即可得预测值，与实际值进行对比，结果见表7。

由表7 数据可知，2009—2014 年碳排放量一直在增长，而山东省发布了《山东省2014—2015 年节能减排低碳发展行动实施方案》后，临沂市的碳排放量有所下降。模型预测结果关联度良好，最大误差仅为5.5%，预测值与实际值基本吻合，因此模型具有实际预测意义。

3.2 各自变量分析

通过对影响碳排放量的各自变量进行分析假设，可以定量地预测未来的碳排放量，因此需要根据临沂市近几年的政策，对5 个自变量进行情景假设或通过灰色预测模型进行预测。

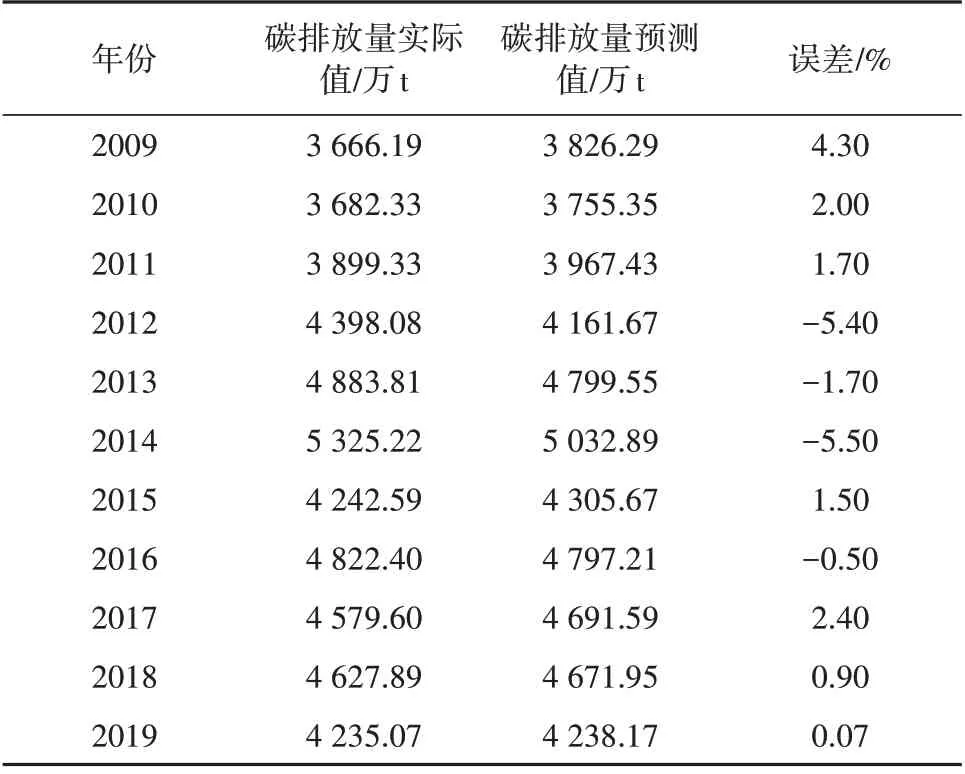
表7 2009—2019年临沂市碳排放量预测值与实际值对比Tab.7 Predicted and actual values of carbon emission in Linyi City from 2009 to 2019

3.2.1 人均工业生产增加值

人均工业生产增加值由年度生产总值乘以工业产值占总产值的比重所得，又由于2009 —2019年生产总值一直稳定上升，工业所占比重不断下降，因此可以用GM（1，1）模型进行预测，2 个值相乘即可得人均工业生产增加值的预测结果。GM（1，1）模型本文不作过多介绍，通过Excel 即可得出预测，见表8。

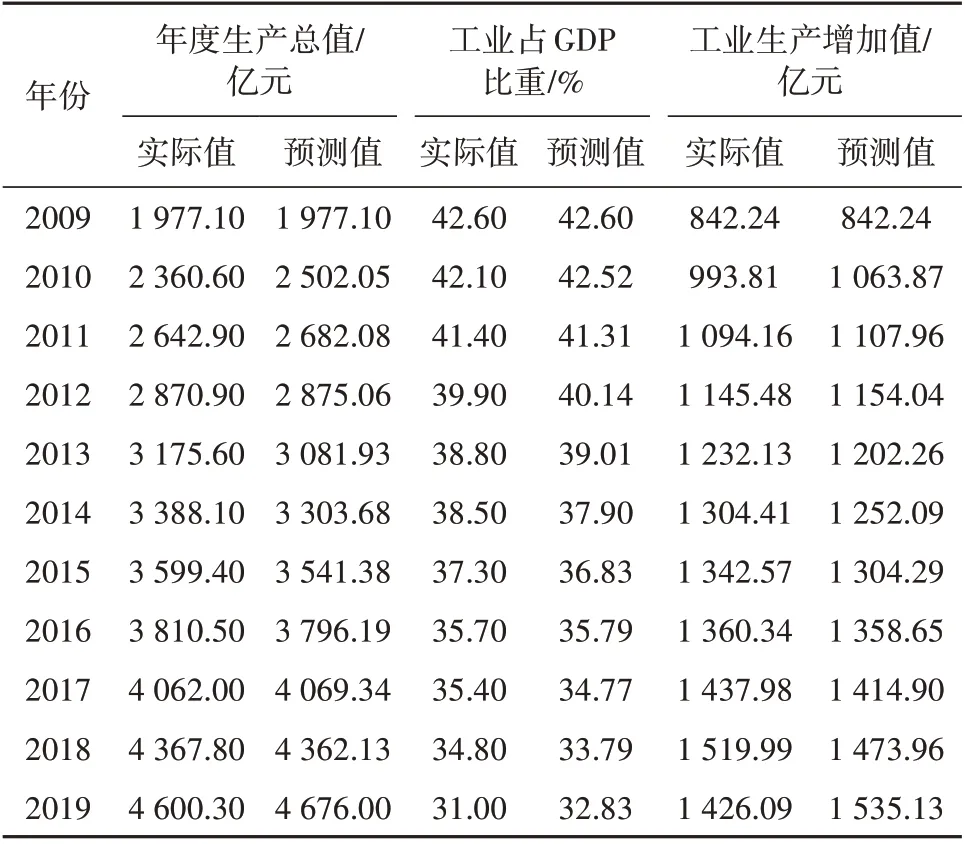
表8 临沂市2009—2019年工业生产增加值预测结果Tab.8 Forecast results of the added value of industrial production in Linyi City from 2009 to 2019

由图3 可以看出：2018 年之前总体预测效果良好，预测结果具有实际意义；而2019 年的预测值明显高于实际值，误差为7.1%。2019 年是本次统计中工业生产总值唯一下降的年份，分析原因为，临沂市在2019年大力推动工业产业结构改革，全市规模以上工业企业营业收入严重下降。而2020 年临沂市工业产业结构得到了及时调整，据2020 年《临沂市统计公报》，其工业生产增加值同比增长7.8%，工业生产增加值为1 537.32 亿元，工业生产水平恢复正常。因此可以认为2019 年的数据并不影响工业生产增加值的整体走势。

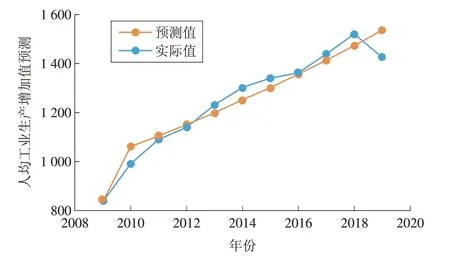
图3 灰色预测模拟值与实际值对比Fig.3 Comparison of grey model simulated value and actual value

按同样的方法可得出2020—2030 年工业生产增加值的预测结果。“十四五”期间面临着新旧动能转换、工业产业结构占比下降等问题，因此2020—2030 年平均用工人数不会超过2020 年的统计用工人数。据2020年《临沂市统计公报》，2020年平均用工人数为393 000 人，考虑到2020 年疫情带来的复工复产问题，2020 —2022 年的平均用工人数取393 000 人。2022—2030 年的平均用工人数按灰色预测模型预测得出，这样便可预测出2020 —2030年的人均工业生产增加值，见表9。

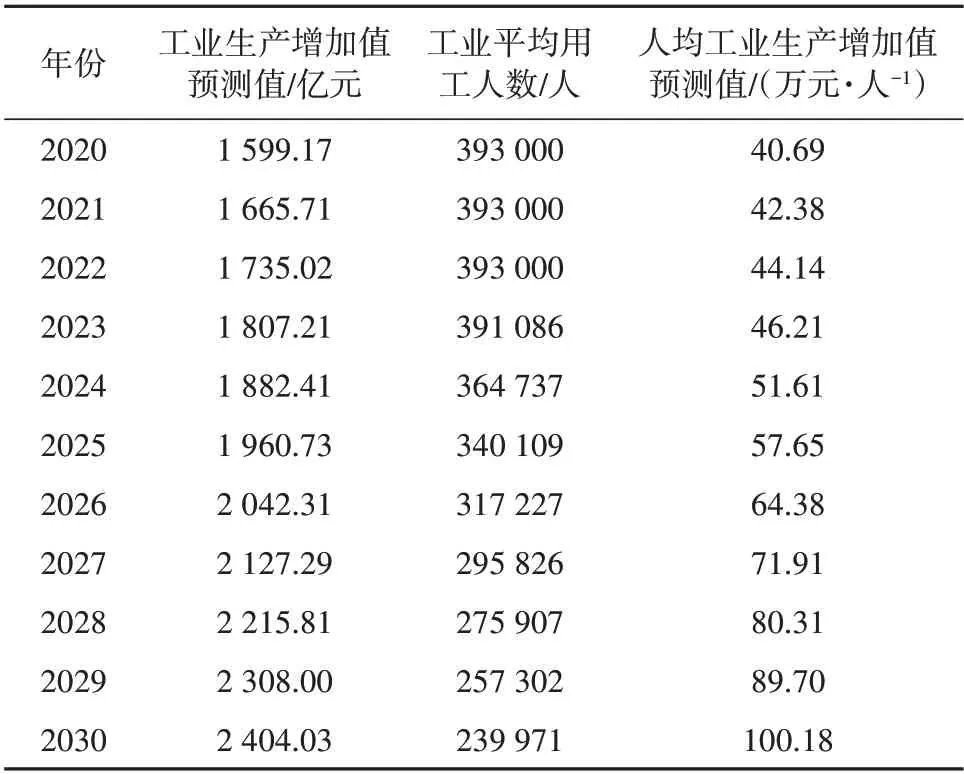
表9 临沂市2020—2030年人均工业生产增加值预测结果Tab.9 Forecast results of per capita industrial production added value in Linyi City from 2020 to 2030

3.2.2 其他自变量

（1）企业固定资产。2020 年以来，疫情导致部分工业企业出现亏损，据统计，2020 年全市规上工业亏损企业为472 家，亏损面为16%，同时考虑到2009—2019年的平均增长率，将企业固定资产分为高速、中速、低速发展模式，增长率≥5%为高速发展，≤-5%为低速发展，在2 个阈值之间视为中速发展。

（2）能源强度和能源结构。“十三五”提出5年单位GDP 能耗下降20.3%，煤炭消费比重下降8.4%，如今“双碳”目标更加强调“低能耗”的发展模式，因此，将能源强度下降作为约束性目标，下降率≥1%为“低耗能”模式，增长率≥1%为“高耗能”模式。从上文中的STIRPAT 模型可以看出，目前减少原煤在总消耗中的占比已经对减排不起主要作用，因此将原煤在总能源消耗量中的占比下调≥1%为“低耗能”模式，上调≥1%为“高耗能”模式。未来工业企业减少净购入电力是降低减排的一个重要措施，按照2009 —2019 年的数据，净购入电力减少率最大为19.4%，增加率最大为6.7%，因此将净购入电力下降率≥5%为“低耗能”模式，增长率≥5%为“高耗能”模式模式。

3.3 发展情景设置及预测

根据STIRPAT 模型，将5 个自变量进行分组设置，其中将能源强度和能源结构（煤炭消耗占比和净购入电力）归为一组，以“高耗能”“低耗能”表示参数的变化，以“高速”“中速”“低速”表示企业固定资产的变化，而人均工业生产增加值按上述灰色预测模型预测的值设定。按参数变化值的不同，将临沂市2020 —2030 年的工业碳排放分为6 种发展情景，见表10。将所有情景下设定的参数值代入式（9）的预测模型，则可得出2020—2030 年的碳排放预测值，见表11。

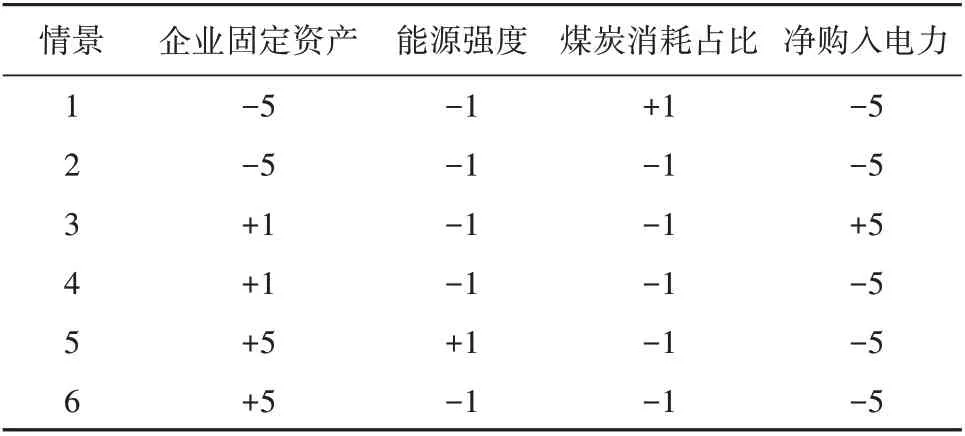
表10 情景假设及参数设置Tab.10 Scenario assumption and parameter setting%

3.4 发展情景分析

表11 显示了山东省临沂市2020—2030 年的工业碳排放预测值。在情景1 中可以看出，当企业固定资产低速增长，能源强度和能源结构在低耗能模式下，碳排放量逐年降低，平均每年碳排放量降低1.82%，是减少碳排放的理想模式。

情景2 在情景1 的基础上，将煤炭消耗占比调成高耗能模式，则在2028年出现了碳排放量的峰值4 337.83 万t。模式2 的碳排放量基本维持在一个水平，平均为4 281.68 万t，较模式1增长了12.8%。

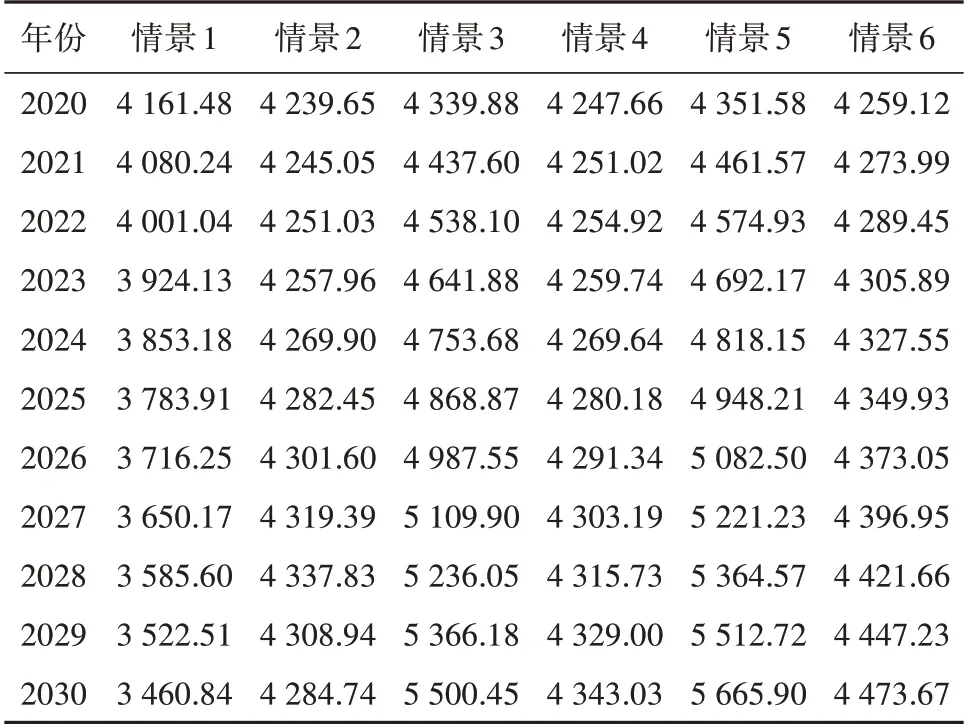
表11 2020—2030年6种情景下的工业碳排放量预测结果Tab.11 Prediction of industrial carbon emission under six scenarios from 2020 to 2030万t

对比情景1 和情景2 可见，煤炭消耗占比对工业碳排放量的影响极大，平均每年增加1%，未来10年平均碳排放量减少6.4%。因此可以推断出，现在工业碳排放量大主要是使用了焦炭等低位发热量较大的燃料，但原煤燃烧带来的污染仍然不能忽视。

其他4种情景下碳排放量均逐年增加且维持在较高水平，其平均碳排放量分别为4 889.10 万t，4 285.95 万t，4 972.14 万t，4 356.22 万t，碳排放量平均年增长率为2.4%，0.2%，2.7%，0.5%。其中在情景5中，即工业经济高速发展、能源强度在高耗能模式、能源结构在低耗能模式下，碳排放量在2030 年达到峰值5 665.90 万t，很显然这种情景是不可取的。

对比情景3 和情景4 可见，净购入电力的变化对工业碳排放量的影响也很大，情景3 在情景4 的基础上，未来10 年平均碳排放量减少14.1%，因此减少工业企业净购入电力是节能减排的重要途径。

对比情景5 和情景6 可见，能源强度直接影响工业碳排放量，情景6 在情景5 的基础上能源强度变化下调2%，未来10 年平均碳排放量可减少14%，因此降低能源强度是国家“十四五”时期必须坚持的目标。要想在保证人均GDP 正常发展的前提下减少碳排放，工业能耗必须稳定下降。

通过纵向对比情景2、情景4 和情景6，在能源强度和能源结构均为低耗能时，3 种企业固定投资模式下的平均碳排放量分别为4 281.68 万t，4 315.53 万t，4 356.22 万t。若企业固定投资每年增加5%，未来10 年的平均碳排放量增加1.7%。因此，保持企业固定资产的低速发展模式可有效地节能减排。

综合分析看，在临沂市工业经济稳定增长的前提下，降低能源强度、优化能源结构对减少碳排放量起着尤为关键的作用；与此同时，适当降低企业固定资产，转变经济发展方式，由要素驱动转为技术驱动，才能从根本上实现节能减排。

4 结论

本文基于STIRPAT 模型建立了临沂市工业碳排放量与企业固定资产、人均工业生产增加值、能源强度、原煤占能源消耗比及净购入电力5 个自变量的关系模型，并通过设置6 种不同的情景模式进行了预测。为响应国家“双碳”目标，结合本次研究结果，对临沂市节能减排提出以下意见。

（1）着力推进传统能源消耗替代，加快能源结构转变。临沂市工业生产中煤炭和石油的消耗量占较大的比重，因此可以通过改变现有的能源消费结构，例如降低传统能源的消耗量，增加天然气的消耗比重，加强对清洁能源、可再生能源的发开和利用。

（2）减少工业能耗下降，降低能源强度。降低能源强度的根本还是提升能源利用效率，需要加大燃料利用技术的引进与创新，投入相应的科研经费，加大对碳排放人才的培养与引进，完善低碳研究体系，向其他低碳企业学习较为先进的理念，促进临沂市的工业碳排放体系完善。

（3）保持工业产值健康稳定增长。不能过分追求工业产值的增加，在企业正常盈利的情况下，实现健康绿色的良性循环发展模式，企业要兼顾好经济增长与低碳的关系。