菲涅尔公式讨论光波反射和折射时振幅的变化*
刘家兴 刘高福 陈德良
(贵州师范学院物理与电子科学学院 贵州 贵阳 550018)
光波是一种电磁波,当光进入两种介质分界面时,传播方向满足反射和折射定律,根据麦克斯韦方程组和电磁场的边值关系可以研究平面光波在两介质分界面上的反射和折射问题,并可用菲涅尔公式来描述其振幅间的关系,菲涅尔公式是大学物理中的一组重要公式,对其相关问题的讨论是大学物理教学研究中的热点[1,2],对后续内容的学习具有重要的作用,但教材中未对反射和折射波的振幅变化作出详细说明,学生也不容易发现其变化关系.笔者根据多年的教学经验,利用菲涅尔公式、电磁波的能量和能流密度等理论,讨论光在界面上的反射系数和透射系数、反射率和折射率等问题,帮助学生深入理解菲涅尔公式和光波振幅的概念.
1 菲涅尔公式
当光波射到两种不同介质的分界面上时,将分成两个波,一个反射波和一个折射波,根据麦克斯韦的电磁理论,以及光的反射定律、折射定律和边值关系,可以得到菲涅尔公式如下[3,4]
(1)
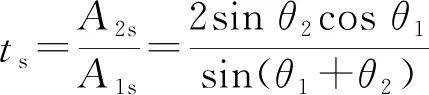
(2)
(3)
(4)
其中A1s和A1p表示入射波垂直分量和平行分量的振幅,A′1s和A′1p表示反射波垂直分量和平行分量的振幅,A2s和A2p表示折射波垂直分量和平行分量的振幅,rs和ts表示s波(即垂直分量)的振幅反射系数和透射系数,rp和tp表示p波(即平行分量)的振幅反射系数和透射系数.
2 反射系数和透射系数
2.1 光从光疏介质入射到光密介质
利用折射定律n2sinθ2=n1sinθ1和三角函数公式,可将式(1)~(4)用折射率n1,n2和入射角θ1表示,当光波由光疏介质进入光密介质,即n1 图1 n1=1,n2=1.3,rs,rp,ts,tp随入射角θ1变化关系曲线 图2 n1=1.3,n2=1.5,rs,rp,ts,tp随入射角θ1变化关系曲线 利用折射定律n2sinθ2=n1sinθ1和三角函数公式,将式(1)~(4)用折射率n1,n2和入射角θ1表示,在光波由光密介质进入光疏介质,即n1>n2时,振幅反射系数rs,rp和透射系数ts,tp随着入射角θ1变化而变化.例如当n1=1.3,n2=1,rs,rp,ts,tp,随入射角θ1的变化关系如图3所示,当n1=1.5,n2=1.3,rs,rp,ts,tp随入射角θ1的变化关系如图4所示.从图可以看出,随着入射角的增大,rs,ts,tp一直在增大,|rp|先减小后增大.在入射角从0~90°整个变化过程中,|rs|≤1,rp≤1,在0≤θ1≤θC的变化过程中,ts>1,tp>1,即折射光s分量和p分量的振幅大于入射光相应分量的振幅,从折射光是入射光的一部分的角度看,好像不满足“能量守恒”定律. 图3 n1=1.3,n2=1,rs,rp,ts,tp随入射角θ1变化关系曲线 图4 n1=1.5,n2=1.3,rs,rp,ts,tp随入射角θ1变化关系曲线 光波是一种电磁波,要考察光波在界面上反射和折射时有没有违背“能量守恒”定律,必须考虑电磁波能量的表示量——坡印廷矢量,它表示单位时间内通过垂直于传播方向的单位面积的能量.其表示为 (5) (6) 又由于折射率 (7) 其中ε0和μ0为真空介电常数和真空磁导率常数,所以当光从光疏介质进入光密介质时,折射率n变大了,在能量相同的情况下,振幅会变小;当光从光密介质进入光疏介质时,折射率n变小了,较小的振动能量也有可能引起较大的振幅,这样就不难理解当光从光密介质进入光疏介质时振幅增大,即违背“能量守恒”定律这一现象. 下面以平面光波为例来证明光波在界面上反射和折射时满足能量守恒定律.已知平面光波单位时间内通过垂直于传播方向单位面积的能量,即光强度为[4] (8) 记入射光波强度为I1,反射光波强度为I′1,折射光波强度为I2,则每秒入射到单位面积上的能量W1、反射波和折射波每秒从分界面出射的能量W′1和W2分别表示为 (9) (10) (11) μ1=μ2=μ0 于是,在分界面上反射波、折射波单位面积上的能量流与入射波单位面积上的能量流之比为 (12) (13) 式中,R和T分别表示能量反射率和能量透射率. 将菲涅尔公式代入上式,可得s波和p波反射率和透射率分别为 (14) (15) (16) (17) Rs+Ts= (18) Rp+Tp= (19) 即在不考虑界面的吸收和散射的情况下,s波和p波的反射率加透射率分别等于1,满足能量守恒定律. 利用菲涅尔公式讨论光波在分界面上的反射和折射时振幅的变化关系,当光从光疏介质进入光密介质时,反射光和折射光的振幅均小于入射光振幅,当光从光密介质进入光疏介质时,反射光的振幅小于入射光的振幅,而折射光的振幅大于入射光的振幅,好像是不满足“能量守恒”定律的一种有趣现象,利用能流密度的概念对这一特殊现象作了讨论,并用平面光波证明了光波在界面反射和折射时,光能量满足能量守恒定律.

2.2 当光从光密介质入射到光疏介质


2.3 关于能量是否守恒的证明

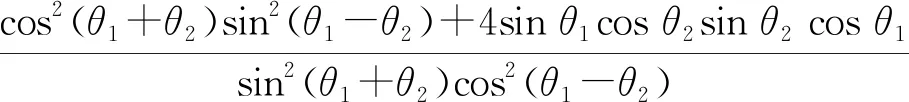
3 结论

