简谐振动在非惯性系中的动力学分析*
米仪琳
(北方工业大学理学院 北京 100144)
1 引言
简谐振动是最简单、最基本的振动,任何复杂的振动都可以分为若干个简谐振动,因此在大学物理教材中重点地探讨了惯性系中简谐振动的基本规律[1~3].那么在非惯性系中,原来做简谐振动的系统是否还在做简谐振动;非惯性系需要满足什么条件;振动的周期和角频率是否还是唯一地取决于振动系统,等等.学生在理解上容易出现错误,文献中也极少涉及[4~6].本文以弹簧振子、单摆复摆为例,系统研究了在各种平动、转动非惯性参照系中,系统做简谐振动的条件和运动规律.
众所周知,当系统位于非惯性参照系中时,系统不仅受到物体间的相互作用力,还受到惯性力的作用[7,8].若选地面为S系,S′系相对S系以加速度a0做加速直线运动.一运动质点相对S系的速度为ν,相对S′系的速度为ν′,则根据牛顿的绝对时空观和伽利略的速度变换方程,运动质点的绝对加速度a、相对加速度a′和牵连加速度a0的关系
a=a0+a′
(1)
若质点所受合外力为F,其运动速度远远小于光速,则质点质量m的相对论效应可以忽略,方程两边同时乘以标量m
ma′=F+(-ma0)
(2)
设f*=-ma0是S′系相对S系加速运动产生的,它是一种非相互作用力,我们把它称为惯性力[8].
当S′系绕静止于惯性系S中某一点O,以角速度ω转动时,质点的绝对加速度a、相对加速度a′的关系,则可以表示为[7]
(3)
其中r是从O点指向质点所在位置的有向线段,ν′是质点相对S′系的运动速度.若质点受到的合外力为F,S′系相对S系做匀角速转动,则在S′系中
ma′=F+mω2r-2mω×ν′
(4)
设离心力
科里奥利力
2 加速平动参照系中谐振动系统的运动
2.1 加速运动小车中的弹簧振子
一劲度系数为κ的轻弹簧连接一质量为m的小球(小球可以看做质点),竖直悬挂于小车内,小车在光滑水平面上以加速度a运动,如图1所示.下面我们分析弹簧振子的运动情况.

图1 加速运动小车里的弹簧振子
选地面为S系,相对地面加速运动的小车为S′系.在S系建立xOy直角坐标系,小车沿x轴正向加速运动.以弹簧振子受力为零的位置即平衡位置为坐标原点,平行弹簧振子方向为O′x′轴,在S′系建立x′O′y′坐标系,如图2所示.

图2 弹簧振子位于平衡位置的受力分析
弹簧振子位于平衡位置O′点时,假设弹簧伸长δ,则在O′点
-κδ+masinθ+mgcosθ=0
(5)
mgsinθ-macosθ=0
(6)

(7)
如果小车运动的加速度a发生变化,弹簧振子的平衡位置会随着加速度a的改变而改变,弹簧振子不再是围绕平衡位置做往复运动.因此,只有小车匀加速运动时,弹簧振子的平衡位置才不随时间发生变化,弹簧振子和竖直方向的夹角θ是固定的,这时系统才有可能做简谐振动.
沿x′轴方向,将弹簧振子拉离平衡位置.假设某一时刻,弹簧振子位于坐标x′处,分析小球的受力情况.该时刻弹簧振子相对竖直位置偏离θ′,则根据式(2),有

(8)
mgsinθ′-macosθ′=0
(9)
由式(7)、式(9),得出
θ=θ′
(10)
式(10)说明弹簧振子在沿x′轴方向运动时,弹簧振子和竖直方向的夹角θ和它的运动状态无关.
由式(5)~(10)可以得出
(11)

x=Acos(ωt+φ)
(12)
振动周期
(13)
由式(5)~(13)得出,在相对地面匀加速平动的小车上,竖直悬挂的弹簧振子仍会围绕平衡位置做简谐振动,其平衡位置与竖直方向有一夹角θ,θ角取决于小车的加速度和弹簧振子所在位置的重力加速度;而振动角频率和周期只取决于振动系统,与小车运动的加速度无关.
采用与上述类似的方法,可以推导出,弹簧振子处于竖直加速平动参照系中(如,弹簧振子悬挂于竖直加速下降的电梯里)时,弹簧振子仍做简谐振动,并且振动角频率、周期只与振动系统有关.
2.2 斜面上的单摆
一倾角为θ(θ很小) 的斜面,静止在水平面上.车沿着斜面以加速度a自顶端滑下,单摆位于一小车内,单摆摆长l,摆球质量为m.下面我们讨论单摆的运动情况.
选地面为S系,沿斜面加速运动的小车为S′系.在S′系建立xOy直角坐标系,x轴沿斜面方向,y轴沿垂直斜面方向,如图3所示.

图3 小车沿斜面加速运动时,单摆位于平衡位置的受力分析
在S′系观察,某时刻单摆所受合力为零,单摆处于平衡位置,此时,单摆和y轴正向夹角α.将单摆受力向x轴、y轴方向分解
ma-mgsinθ-Tsinα=0
(14)
Tcosα-mgcosθ=0
(15)
则在小车相对斜面加速运动时,若悬挂于小车上的单摆处于平衡位置,单摆和y轴正向之间的夹角α满足
(16)
斜面倾角θ很小,则
(17)
若小车沿斜面加速运动时,加速度a随时间发生变化,则单摆的平衡位置也会随着加速度a发生变化,单摆将不再做简谐振动.
假设小车沿斜面做匀加速运动,将单摆拉离平衡位置,单摆开始运动,某一时刻单摆偏离平衡位置Θ,如图4所示,单摆和y轴方向之间的夹角为α+Θ,在S′系建立自然坐标系,取逆时针方向为转动正方向.

图4 小车沿斜面匀加速运动时,单摆的受力分析
分析单摆的受力情况,列出其动力学方程
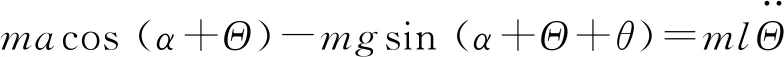
(18)
(19)
由式(18)得出

(20)
若单摆偏离平衡位置的角度Θ很小,α也很小,斜面倾角θ也很小,则由式(14)~(20)得到
(21)

Θ=Θmcos(ωt+φ)
(22)
单摆运动的周期
(23)
式(14)~(23)说明,在单摆摆角Θ、斜面倾角θ很小,并且α也很小的情况下,单摆做简谐振动,并且其振动的角频率ω、周期T只取决于振动系统.在这里α是单摆处于平衡位置时和y轴方向的夹角,由式(17)可以看出α与小车运动的加速度密切相关.α很小,则要求小车运动的加速度满足
a-gθ≪g
(24)
即当a≪g时,单摆的运动才是简谐振动.
如果斜面倾角θ=0,则对应着单摆悬挂在小车上,小车在地面上沿水平方向以恒定加速度运动的情况,如图5所示.

图5 小车在水平面上匀加速运动时,单摆的受力分析
单摆处于平衡位置时,和竖直方向的夹角α,由式(17) 可以看出,此时
(25)
将单摆拉离平衡位置Θ,由式(18)、(19)可以给出在自然坐标系中,单摆的动力学方程
(26)

Θ=Θmcos(ωt+φ)
(27)
单摆运动的周期
(28)
单摆此时做简谐振动.由式(24)可以得出,α很小,则要求
a≪g
(29)
由以上的讨论可以看出,无论小车是在地面上,还是在静止的斜面上做匀加速运动,当小车运动的加速度a远远小于重力加速度g,并且单摆摆角Θ、斜面倾角θ都很小的情况下,单摆在加速平动的小车内仍围绕其平衡位置做简谐振动,振动周期只与振动系统和单摆所在位置的重力加速度有关,与单摆是否处于惯性系中无关.
2.3 加速运动电梯中的复摆
以加速度a向上运动的电梯内有一钟摆,如图6所示,分析钟摆的运动.
钟摆对悬挂点O的转动惯量为J,质心为C,悬挂点O到质心的距离OC=r.某一时刻,钟摆偏离平衡位置,与竖直方向夹角为θ(θ很小),如图6所示.

图6 电梯加速上升时,钟摆的受力分析
以逆时针方向为转动正方向,根据刚体的角动量定理,可以得出

(30)
令
则钟摆定轴转动的动力学方程
(31)
钟摆转动的运动学方程
θ=θmcos(ωt+φ)
(32)
处于加速上升电梯中的钟摆,在摆角θ很小的情况下,仍做简谐振动.其周期
(33)
与在惯性系中不同的是,钟摆简谐振动的角频率和周期不仅与振动系统、钟摆所在位置的重力加速度g有关,还与电梯的加速度密切相关,钟摆简谐振动的角频率会随着电梯加速度的增大而增大.
3 转动参照系中的弹簧振子
一圆盘以角速度ω′绕通过盘心C点的竖直光滑轴转动,如图7所示.一劲度系数为κ、质量为m的弹簧振子固定于盘心,置于沿圆盘半径方向的光滑槽内.分析弹簧振子的运动情况.

图7 匀速转动圆盘上的弹簧振子及其受力分析
选地面为S系,匀速转动的圆盘为S′系.在S′系,以弹簧振子的平衡位置为坐标原点,沿径向凹槽建立Ox直角坐标系,分析弹簧振子的受力情况.


假设弹簧原长l0,弹簧振子处于平衡位置时,弹簧振子受力为零,弹簧伸长δ.则有
-κδ+mω′2(δ+l0)=0
(34)
拉伸弹簧振子离开平衡位置,某一时刻,弹簧振子处于坐标x处,于是
(35)
弹簧振子的动力学方程
(36)
令
则弹簧振子此时的运动学方程
x=Acos(ωt+φ)
(37)
所以,处于相对地面匀速转动的圆盘上,弹簧振子仍做简谐振动.其周期
(38)
因此只有当圆盘匀速转动时,弹簧振子的运动才是简谐振动,并且弹簧振子振动的角频率ω和周期T不仅与弹簧的劲度系数κ、弹簧振子的质量m有关,还取决于圆盘转动的角速度ω′,并且会随着角速度ω′的改变而改变.这与弹簧振子处于惯性参照系、加速平动参照系中完全不同.弹簧振子处于上述参照系中时,弹簧振子做简谐振动,并且振动的角频率ω和周期T只和振动系统有关,和其他因素无关.而在转动参照系中,弹簧振子仍做简谐振动,但振动的周期T和角频率ω与转动参照系的角速度ω′密切相关,不再唯一取决于振动系统弹簧振子.
4 结论
我们借助于惯性力,研究了处于不同非惯性系中的弹簧振子、单摆、复摆的运动,得出了非惯性系中简谐振动的条件和运动规律.研究发现,当谐振动系统处于非惯性系时,系统是否仍做简谐振动,与我们所选用的非惯性参照系和振动系统密切相关.系统只有处于匀加速平动参照系或匀速转动的参照系时,平衡位置才不随时间发生变化,系统才有可能围绕平衡位置运动.弹簧振子无论处于匀加速平动参照系还是匀速转动的参照系中,都依旧做简谐振动.只是在转动参照系中,弹簧振子振动的周期T和角频率ω与转动参照系的角速度ω′密切相关,不再唯一取决于振动系统;而处于水平加速平动参照系中的单摆,则在摆角Θ很小、斜面倾角θ很小(或θ=0),同时平动参照系加速度a远远小于重力加速度g(a≪g)时,系统才做简谐振动,其振动周期T与系统是否处于惯性系无关,仍然仅与振动系统和重力加速度g有关;而处于竖直加速的平动参照系中的复摆,只要是做小角度摆动,其运动就仍然是简谐振动,但是与水平加速平动参照系中的单摆不同的是,位于竖直加速的平动参照系中的复摆,其振动角频率ω和周期T不仅与振动系统、重力加速度g有关,还与平动参照系的加速度a密切相关.本文为非惯性系中的简谐振动建立了清晰的物理图像,这将有利于加深学生对简谐振动的理解,提高学生分析问题、解决问题的能力.

