中间支撑轴向运动微梁的横向振动研究
刘慧贤,随岁寒
(1.商丘工学院 基础教学部, 河南 商丘 476000; 2.商丘工学院 机械工程学院,河南 商丘 476000)
微机电系统因其能耗低、体积小和智能化程度高等优点,已被广泛应用于汽车、通信、自动控制和军事等领域[1]。梁是微纳米材料的常用结构形式,当梁的厚度达到微米量级时,便会出现所谓的尺寸效应。Mindlin等[2-3]提出的偶应力理论克服了经典理论不能准确表达微纳米结构力学性能的不足,采用了2个材料内秉特征尺寸参数。由于材料内秉特征尺寸的确定存在困难,故减少内秉特征尺寸参数的个数对实验研究和理论分析具有实际意义。Yang等[4]提出的修正偶应力理论只包含1个材料内秉特征尺寸参数。
考虑到一些工程应用如传动带、带锯等模型化为轴向运动系统并可应用于微机电系统,而这些结构的横向振动往往对其正常工作产生不利影响,所以研究轴向运动微梁的横向振动对工程设计有重要意义。目前,轴向微结构研究主要集中在利用非局部理论方面[5-7],如Marynowski[8]利用修正偶应力理论研究了轴向运动微尺度面板的横向振动。在工程应用中,梁类连续体系统往往受到集中质量或弹簧等的作用[9-12],故研究轴向运动微梁在弹簧支撑作用下的动力学特性对工程设计具有指导意义。
本研究利用修正偶应力理论,通过虚功原理导出中间支撑轴向运动微梁横向自由振动控制方程,采用有限差分法作为求解工具,分析了轴向速度、梁厚度、弹簧刚度和预应力对前两阶固有频率的影响,并将部分结果与经典理论所得结果进行了对比。本研究也探讨了临界速度与预应力和弹簧刚度的关系,在轴向运动系统中,轴向运动速度超过临界值便会发生失稳,对结构造成破坏。
1 物理模型
采用虚功原理推导轴向运动微梁的控制方程,应用有限差分法求解系统固有频率。
1.1 控制方程
建立轴向运动微梁坐标系,速度v沿x轴正向,梁宽为b,厚为h,两支撑间的长度为L,如图1所示。

图1 轴向运动微梁示意图Fig.1 Schematic of an axially moving microbeam
根据Yang等[4]提出的修正偶应力理论,采用Euler梁模型,则梁的应变能变分为
(1)
弹簧势能变分为
(2)
式中:δ(x)是狄拉克函数。
(3)
惯性力做功的变分为
(4)
结合式(1)、(2)、(4),代入如下虚功原理表达式:
δU+δU1=δV。
(5)
分步积分后得到
(6)
对于式(6),由于δw的任意性,并忽略边界条件项,可得到轴向运动微梁系统控制方程:
(7)
若式(7)中的材料内秉特征尺寸l为0,则修正偶应力模型退化为经典的Euler梁理论模型。
微梁两端简支的边界条件为
(8)
(9)
设控制方程(7)的解为
w(x,t)=W(x)eωt,
(10)
式中:W(x)是模态函数;ω是固有频率,rad/s。将式(10)代入式(7),得
(11)
1.2 有限差分法[14]的应用
沿梁长度等间距划分节点并编号为1~n,其中编号1和n位于边界上。 为便于运算,将弹簧支撑点设置在一个节点上,i0为弹簧支撑点对应的节点编号。 式(11)中各阶偏微分用相应节点值表达如下:
(12)
(13)
(14)
将式(12)至(14)代入式(11),得到
(15)
式中:i=1,2,3,…,n-1。
类似地,对边界条件式(8)和式(9)的处理如下:
W0=Wn=0,
(16)
W-1=-W1;Wn+1=-Wn-1。
(17)
将式(15)结合式(16)、(17)整理成矩阵形式:
Mω2+Cω+K=0。
(18)
式(18)是一个广义复特征方程,其中M、C和K分别称为质量矩阵、陀螺矩阵和刚度矩阵,这3个矩阵均为(n-2)×(n-2)方阵。 求解式(18)即可得到固有频率ω,为便于工程参考,将其转化为以Hz为单位的固有频率,即
(19)
2 数值算例
采用环氧树脂材料,弹性模量E=1.44 GPa,泊松比υ=0.38,l=17.6 μm,弹簧支撑点坐标x0=L/2,梁厚度h=20 μm,b=2h,L/h=20,σ0=1 MPa,k= 3×106N/m。
图2和图3为前两阶固有频率与轴向运动速度的关系,并给出了经典理论下相应的固有频率。两种理论下,轴向运动微梁的振动特性规律类似,即速度越大、固有频率越小。第1阶和第2阶频率在修正偶应力理论下的解约为经典理论解的2倍,尺寸效应明显。

图2 第1阶固有频率与轴向运动速度的关系Fig.2 First mode frequencies vs axial velocity
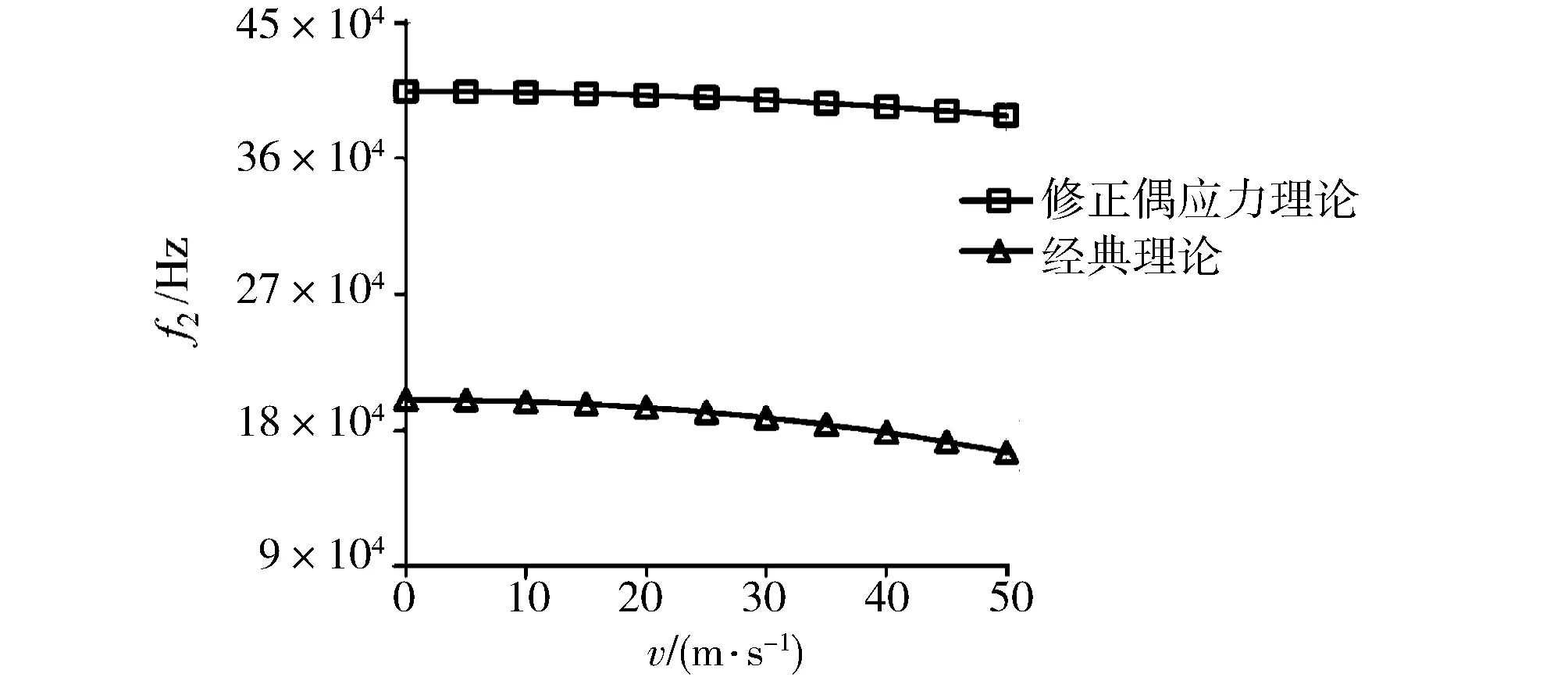
图3 第2阶固有频率与轴向运动速度的关系Fig.3 Second mode frequencies vs axial velocity
表1和表2分别为前两阶固有频率解随梁厚度变化的规律,梁厚度在20 μm时最接近材料内秉特征尺寸l,所以梁厚度在20 μm时前两阶频率在两种理论下结果的差值百分比最大。随着厚度的增大,这一差值逐渐变小,即厚度大于内秉特征尺寸参数的条件下,厚度越大则尺寸效应越不明显。

表1 第1阶固有频率与梁厚度的关系(v=40 m/s)Tab.1 First mode frequencies vs beam thickness(v=40 m/s)

表2 第2阶固有频率与梁厚度的关系(v=40 m/s)Tab.2 Second mode frequencies vs beam thickness(v=40 m/s)
图4和图5给出了预应力对前两阶固有频率的影响,在应力从1 MPa增至20 MPa的过程中,前两阶固有频率分别增加了约50%和17%。图6给出了前两阶模态函数,可见第1阶模态在x=L/2时幅值最大,而第2阶模态在x=L/2时幅值为0。由于弹簧支撑点坐标x0=L/2,所以弹簧支撑对第2阶固有频率的影响可忽略,但对第1阶固有频率有一定影响,弹簧刚度变化时第1阶固有频率增幅约为10%,而第2阶固有频率不变,如表3所示。

图4 预应力对第1阶固有频率的影响Fig.4 First mode frequencies vs pre-stress

图5 预应力对第2阶固有频率的影响Fig.5 Second mode frequencies vs pre-stress
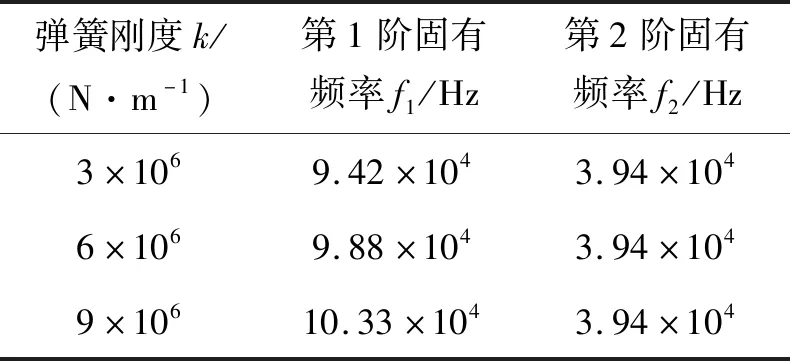
表3 弹簧刚度对前两阶固有频率的影响(v=40 m/s)Tab.3 First 2 mode frequencies vs spring stiffness(v=40 m/s)

图6 前两阶模态函数(v=40 m/s)Fig.6 First 2 mode functions(v=40 m/s)
为求得临界速度,可略去式(15)中与频率相关的量,得
(20)
式中:i=1,2,3,…,n-1;vc代表临界速度。结合边界条件式(16)和式(17),整理式(20)可得
(21)
式(21)是一个标准特征值问题,求解可得各阶临界速度。图7给出了前两阶临界速度与预应力的关系,可见预应力越大则临界速度越大。在应力从1 MPa增至20 MPa的过程中,前3阶固有频率分别增加了约50%和17%,与图4和图5反映的预应力对固有频率的影响规律类似。表4给出了临界速度与弹簧刚度的关系,弹簧刚度从3×106N/m增至9×106N/m时第1阶临界速度增加7.7%,而第2阶临界速度不变,这里同样可以理解为弹簧支撑在梁中点位置对第2阶模态振动的影响可忽略。

图7 临界速度与预应力的关系Fig.7 Critical velocity vs prestress
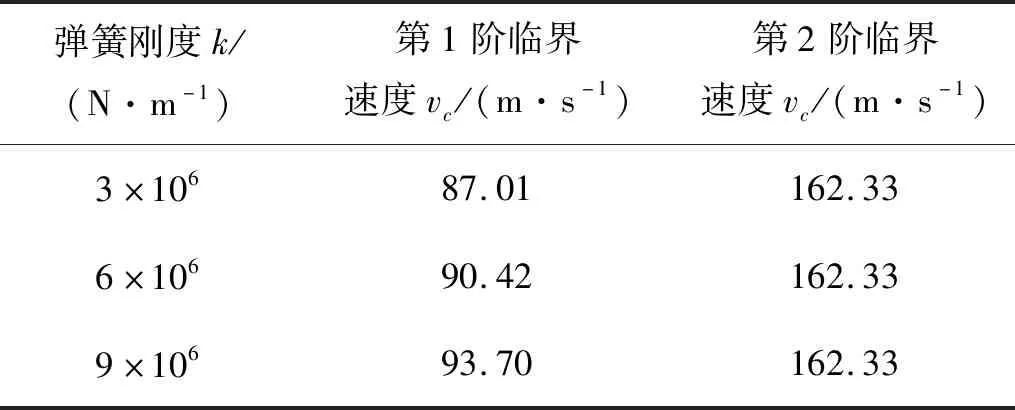
表4 弹簧刚度对临界速度的影响Tab.4 Critical velocity vs spring stiffness
3 结论
基于Euler梁模型和修正偶应力理论,结合虚功原理导出中间支撑轴向运动微梁横向自由振动控制方程,利用有限差分法离散控制方程,分析了轴向速度、梁厚度、弹簧刚度等参数对前两阶固有频率的影响,并将部分结果与经典理论所得结果进行了对比,探讨了临界速度与预应力和弹簧刚度的关系。结论如下:轴向速度增大则固有频率降低;材料内秉特征尺寸参数对梁的振动特性影响显著;各阶固有频率随着轴向预应力的增大而增大;预应力增大导致临界速度增大;弹簧对固有频率和临界速度的影响不仅与弹簧刚度有关,而且与布置位置有关。

