罗拉牵伸中须条变细曲线的随机模拟

严广松，汤 聪

(1.郑州升达经贸管理学院 应用数学研究所，河南 郑州451191；2.郑州升达经贸管理学院 建筑工程学院，河南 郑州451191)

最早使用计算机对牵伸过程进行模拟的是Johnson[1],他利用简单牵伸的理想状态，给出了牵伸须条弹性的特征，认为须条弹性对牵伸不匀的影响可以忽略。苏玉恒等[2]分析了纤维在牵伸区的性态，将纤维在牵伸区的变速点看作具有一类抛物线型密度函数的分布点，给出了须条在牵伸区变细曲线的随机模拟。Yan等[3]在假设须条中的纤维具有一定长度分布的情况下，提出了纤维头端在牵伸区变速点具有抛物线形概率密度函数的特征，并且计算了这个抛物线概率密度函数族的条件期望和条件方差。还有一批学者使用其他物理方法对牵伸区纤维的变速现象进行建模，从纤维变速行为的分析方面给出了有意义的结论[4-8]。这些研究不但有助于进一步认识牵伸过程，而且有利于改善牵伸的设计，为牵伸技术的突破打下了基础。

尽管前人在罗拉牵伸的研究中做了大量工作，但人们对牵伸的认识仍然需要进一步深化。本研究在假设纤维变速点集中在前罗拉钳口的条件下，给定一种纤维长度分布，并假设输入的须条截面是绝对均匀的，利用瞬间纤维的位置关系，给出了动态过程中牵伸须条变细曲线的随机模拟。

1 模拟的数学模型

在对罗拉牵伸系统进行数学模拟之前，首先要用数学方式来表达罗拉牵伸过程的几个部分——须条、纤维长度和牵伸机制(包括纤维在牵伸区的变速点等)，同时要给出模拟过程中的算法。本研究采用牵伸区瞬间纤维的位置关系，描述了动态纤维的运行规律。

1.1 须条形态的数学表示

要对罗拉牵伸过程进行数学模拟，一个重要的步骤就是要解决须条的数学表示问题。只有将须条的结构和性态表示到一个数学框架中，才能在模拟中有效地进行计算，从而得到各种参数对牵伸的影响。

假设进入牵伸装置前的须条由棉纤维组成，纤维在须条中伸直、平行；须条沿着长度方向是均匀的，其截面纤维根数在沿须条长度方向的各个点几乎是不变的。在这样的假设下，得到了以下两种棉纤维须条数学表达形式。

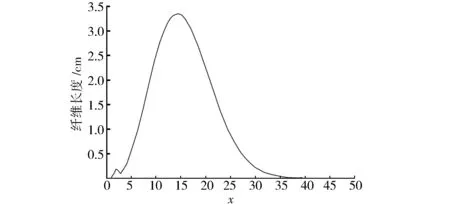
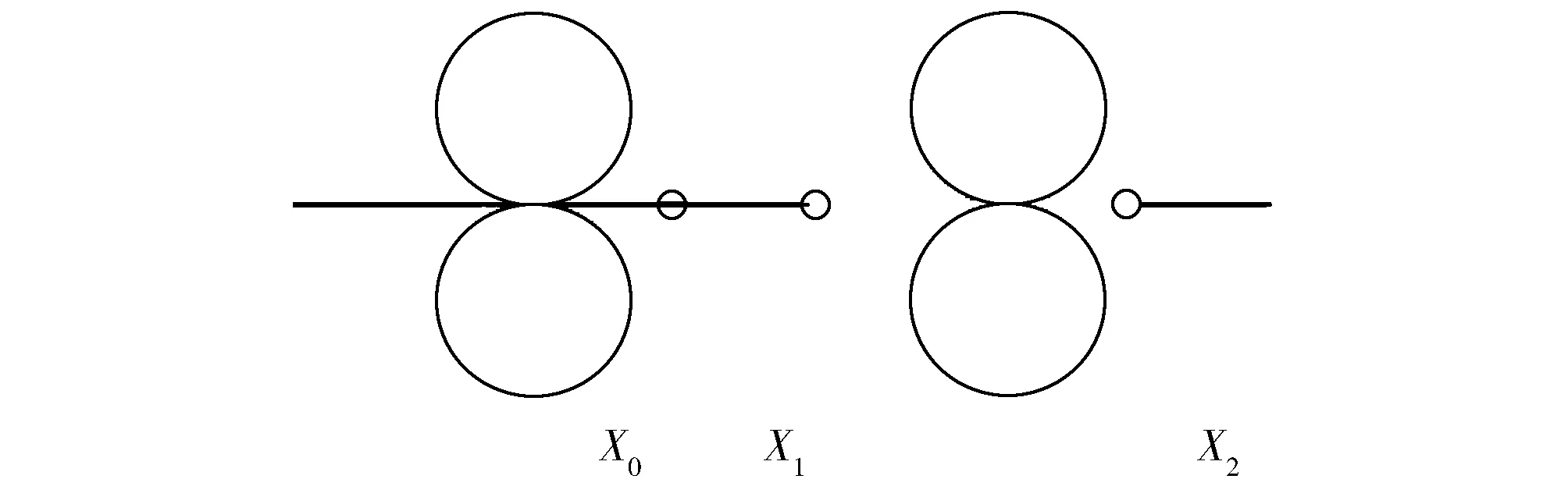
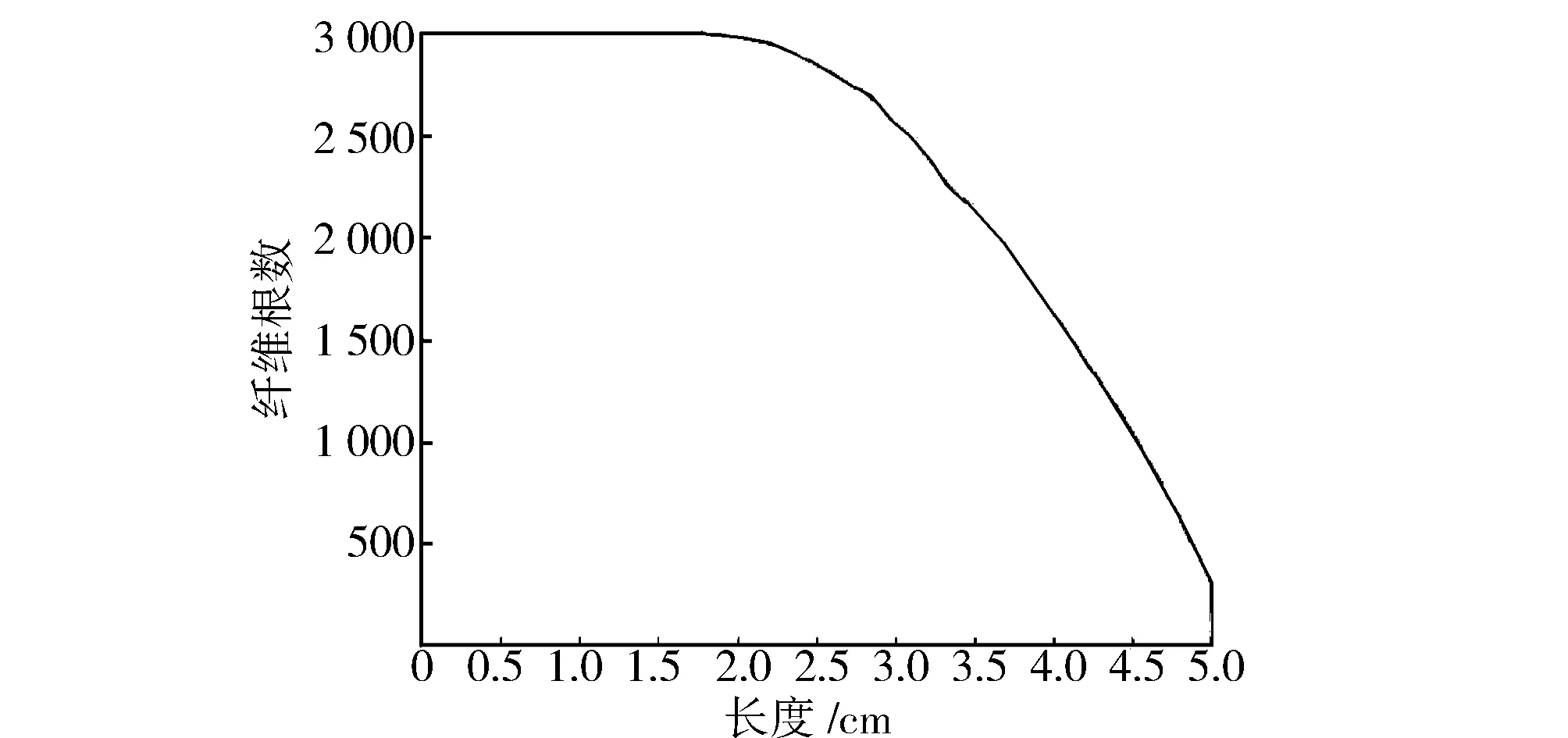
方法A：棉纤维的长度具有概率密度函数f(x)，0

(4)茶树喜阴、需漫射光，茶园周边的植被类型以针阔叶、乔木林混杂为宜，野生兰草对茶叶香气提升具有重要作用；

图1 通道构成须条示意图Fig.1 Sliver containing channels

图2 带有间隙的纤维通道Fig.2 Fiber channel with distance between fiber ends

1.2 纤维长度的表示

在对罗拉牵伸系统进行模拟时，要考虑须条中纤维的长度分布。棉纤维的长度分布或整齐度不仅影响纱线质量，而且对牵伸效果有着很大影响。

本研究采用的棉纤维长度分布是根据Cui等[9]在2009年给出的表示法得到的。按照文献[9]的方法，任一个棉纤维的长度分布概率密度函数都可以表示为两个双参数Weibull分布的凸组合，也就是采用5个参数即可比较准确地表示一个棉纤维长度分布的概率密度函数。棉纤维长度分布的概率密度函数如下：

f(x;α,λ1,θ1,λ2,θ2)=αfi(x;λ1,θ1)+(1-α)f2(x;λ2,θ2)，

式中：fi(x;λi,θi)=λθxλ1-1e-θx2,x>0,λi<0,θi>0,i=1,2。这里取α=0.229、λ1=2.114、λ2=3.481、θ1=1.336、θ2=0.007,得到一个棉纤维的概率密度函数，见图3。

图3 棉纤维长度的概率密度函数Fig.3 Density function of fiber length

1.3 牵伸区纤维运动的模型

图4是罗拉牵伸系统。要对牵伸区纤维的运动进行模拟，首先假设牵伸须条中纤维的长度具有概率密度函数f(x)，其中0

图4 罗拉牵伸系统Fig.4 Roll drafting mechanics

设X0表示某一时刻被后罗拉夹持的纤维在右边露出的长度，X1是X0右边相邻的纤维长度，X2是与X1右边相邻且还在牵伸区内的纤维长度，X3则是被前罗拉夹持的纤维。X1、X2、X3等都是随机变量，它们相互独立且同分布，具有共同的概率密度函数f(x)。对于X0，有

X0=ξ·Y，

(1)

式中：Y是一个与X1、X2、X3等都独立的随机变量，密度函数是f(x)；ξ～U(0，1)是一个与Y独立的随机变量。这样，就表示了纤维一根根首尾相接进入牵伸区但在牵伸区的纤维根数不定的情况。

实际上，不会出现纤维在牵伸区始终首尾相接的情况。因为X3从前罗拉钳口伸出便被夹持，并以v2的速度被拉开，于是就出现了下面两种情况，如图5和图6所示。

图5 通道里的纤维被断开Fig.5 Separated fibers in the drafting zone

图6 纤维在牵伸区内出现断开Fig.6 Separated fibers in the drafting zone

根据以上分析，就有了罗拉牵伸模拟的步骤：

(1)给定参数L(牵伸罗拉隔距)、v1(后罗拉表面线速度)、v2(前罗拉表面线速度)、f(x)(纤维长度的概率密度函数)。

(2)生成一个Y～f(x)，再生成一个ξ～U(0，1)，按照公式(1)计算出观察值x0，其中随机变量ξ与随机变量Y独立。

(3)利用X1～f(x)生成一个观察值x1，判断x0+x1是否大于L。若x0+x1

在以上步骤中，任何一个纤维首尾相接的通道在经过牵伸系统时总能产生一个函数g(x)或者h(x)，假设须条截面中有N个通道，就可以产生N个函数g(x)或者h(x)。将它们叠加起来，就得到了牵伸区须条的变细曲线，其中函数h(x)的叠加就是须条在牵伸区截面中快速纤维的根数。

2 模拟的主要结果

按照上述模型，使用MATLAB软件编程就可以得到相应的牵伸模拟结果。这里主要分析罗拉牵伸的参数对牵伸中须条变细曲线的影响与前罗拉钳口处纤维量的变化(这个变化实际反映的是须条的均匀度)。

2.1 一种纤维长度分布下的模拟

给定纤维长度的一个概率密度函数，给定牵伸隔距和牵伸倍数，后罗拉表面的线速度为20 m/min。经过上述步骤的模拟，得到图7。从图7中可以看出，在输入须条截面纤维根数为3 000时，可以看到变细曲线的趋势是平滑的。在图7中还可以看到被加速的纤维根数的曲线，越接近前罗拉，这个曲线就越高。这些结论与以往的文献一致，说明本模型能够反映罗拉牵伸的真实性。

图7 变细曲线和快速纤维曲线Fig.7 The attenuation curve and the curve for accelerated fibers

从图7中可以看到，由于牵伸倍数选定的是5，所以左边须条截面纤维根数是3 000，而右边须条截面纤维根数在600左右，快速纤维的根数平滑地增长到了前罗拉钳口。

2.2 不同牵伸倍数的模拟

罗拉牵伸研究的一个重要目标就是希望能增大牵伸倍数，也就是前后罗拉线速度之比。这里分别采用牵伸倍数为10和15进行模拟，并记录牵伸中前罗拉钳口处纤维根数的变化。图8与图9分别是牵伸倍数为10和15时的须条变细曲线。

图8 牵伸倍数为10时的变细曲线Fig.8 Attenuation curve with R=10

图9 牵伸倍数为15时的变细曲线Fig.9 Attenuation curve with R=15

通过同一设定条件的多次模拟，记录前罗拉钳口处纤维根数的变化，计算数据的变异系数，可以看出随着牵伸倍数的增大，变异系数呈现非线性增大的趋势。这种趋势说明，牵伸机构本身存在一个固有的降低须条均匀度的规律。

3 结论

通过一种静态的随机建模方法，分析了罗拉牵伸的动态变化规律，给出了符合罗拉牵伸实际的模拟结果，对于进一步认识牵伸系统具有指导意义。本模型在模拟过程中将一些条件简单化，比如须条的均匀度设定和变速点的假设，但不影响最终的模拟结果。 从随机模拟的结果来看，可以得出以下结论：

(1)当纤维在牵伸区的变速点在前罗拉钳口时，须条的变细曲线基本是上凸的。

(2)当牵伸倍数增大时，前罗拉钳口处纤维量的波动增大。

(3)当增大牵伸区罗拉隔距时，牵伸后的须条均匀度变差。

(4)模拟结果与实际牵伸的原理较好地吻合了，说明模型是有效的。

按照本模型的算法，后续将进一步对简单牵伸的各种情况进行模拟，比如对等长纤维须条的牵伸，对各种具有不同纤维长度分布的须条的牵伸，对纤维运动不同变速点分布的牵伸等，从而得到影响牵伸须条均匀度的因素和更加符合实际的模拟结果。