电极曲率对同轴介质阻挡放电非线性行为的影响
周志向郭雪刘富成王晓菲
(河北大学 物理科学与技术学院,河北 保定 071002)
介质阻挡放电是产生大气压均匀放电常用的方式之一,目前已被广泛应用于材料改性、臭氧合成、消毒灭菌等众多领域[1-3].放电稳定性是低温等离子体源的一个重要指标,如何在大气压下获得稳定的均匀放电一直是人们研究的热点[4-5].
介质阻挡放电是一个具有高度非线性的空间延展性系统,它可以呈现出各式各样的非线性动力学行为,例如时空斑图结构、孤立子结构、倍周期分岔现象以及时空混沌[6-8].因此研究这些非线性行为对于控制放电的稳定性以及优化放电参数具有重要的物理意义.在过去十几年内,国内外相关研究者对大气压介质阻挡放电的非线性现象进行了一些探索研究[7-14].例如大连理工大学的Wang等[9-11]通过数值模拟的方法首先在大气压氦气辉光放电中获得了各种非线性行为,例如多倍周期放电、准周期放电和混沌,并系统研究了各种放电参数(例如驱动频率、电压波形、放电间隙、气体成分等)对非线性行为的影响.华南理工大学的戴栋小组从实验上证实了介质阻挡辉光放电中各种非线性行为的存在性[12],并分析了正柱区消散特性对非线性行为的影响[13].
纵观大气压介质阻挡放电非线性行为研究的现状不难发现,这些研究主要集中在了平板型电极结构,对于其他电极结构下的放电行为研究的却很少[15].研究表明电极几何结构是影响放电性质的一个重要因素[16].与常见的平行平板介质阻挡放电结构相比,同轴介质阻挡放电结构可以更好地提高放电的电离特性,易于产生活性较高并且均匀的等离子体[17],实际应用较为广泛,单从工业应用的角度来看,同轴介质阻挡放电的反应器不仅适用于分解气体污染物的非热等离子体,还适用于降解水溶液中的药物污染物[2].最近,Zhang等[18]使用一维流体模型研究了同轴型介质阻挡辉光放电中的非线性现象,通过增加驱动频率或间隙发现了倍周期分岔和混沌等一系列非线性现象,且研究发现电极曲率对单脉冲放电时电流的不对称度有较大影响,但是文中没有研究电极曲率对非线性行为的影响.
本文采用自洽的一维等离子体流体力学模型,详细研究了电极曲率对同轴型大气压介质阻挡辉光放电非线性行为的影响.
1 模型
图1给出了一个典型的同轴型介质阻挡放电结构装置示意.放电发生在2个同轴圆柱形金属电极之间.图1中R为内电极的半径,驱动电压为正弦交流电压,与内电极相连,其幅值为2 k V,驱动频率为20 k Hz.外电极与地相连,半径长度为R2.外电极内侧覆盖一层厚度1 mm,介电常数εr=9的电介质,放电间隙恒定为5 mm.工作气体为氦气,气压p=105Pa,气体温度为300 K.

图1 同轴介质阻挡放电结构示意Fig.1 Schematic diagram of setup for co-axial dielectric barrier discharges
为了简便起见,本文忽略所有其他非线性来源,例如复杂的化学动力学、非局域性行为、边界条件等,使用基本流体模型进行数值模拟[9-11].在数值模拟的过程中,本文仅考虑了2种带电粒子,即电子(e)和氦离子(He+).在迁移扩散近似的基础上,使用连续性方程和动量方程来表示粒子的输运过程

粒子数密度用n表示,粒子流密度用j表示;扩散系数和迁移率分别由D和μ表征;电子e和离子i作为下标,源项用S表示.本文只研究了2种反应过程,即直接碰撞电离和复合,用方程表示为

这里α与β分别为汤森第一电离系数和第二电离系数[9].一般利用泊松方程对空间电场E进行求解.为使运算速度得到提升,本文不使用泊松方程,而选择电流的连续性方程将之取代,即
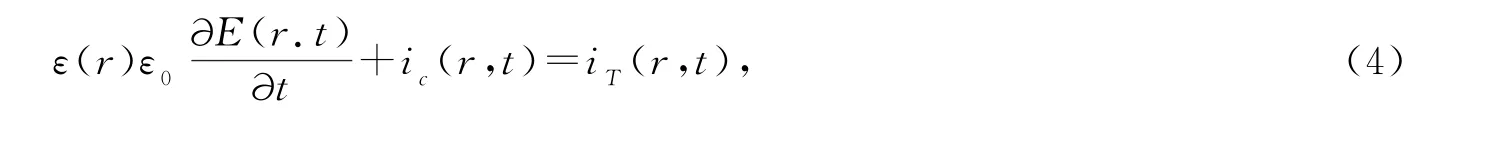

因此外电极处的电流密度为

本文主要目的是探究电极曲率对非线性放电的影响,对于边界条件的选取,为了削弱二次电子发射等边界条件引起的非线性效应,采用第一类边界条件,即边界处的电子和离子密度均为常数.由于存在电介质,所以在其表面会积累电荷,介质表面积累的电荷密度通过对带电粒子通量的时间积分获得,即

为了验证模型的正确性,通过设置与模拟研究[18]和实验研究[19]相同的参数,模拟结果与文献中的结果定量吻合,与实验结果仅仅在定性上吻合,即在相同的参数范围内都获得了倍周期分岔放电和混沌放电现象.实验和模拟上差距一方面来源于仿真模型使用了大量的简化过程,另一方面也是由于影响介质阻挡放电非线性动力学行为的因素太多,因此两者很难从定量上吻合.
2 模拟结果与讨论
电子和离子的初始密度都设定为107cm-3.一般情况下,经过一定的放电周期后,放电就可以达到稳定.本文至少运行了100个周期,确保放电已达到稳定状态.
图2给出了R=0.5 mm 时的电压电流密度波形以及相应的气体电压Ug和表面电荷密度σ随时间的变化曲线.放电电流呈现脉冲形式,在每一个驱动周期内均放电2次,一次位于前半个周期,称之为正脉冲放电,另一次位于后半个周期,称之为负脉冲放电.每经过一个驱动周期,正负脉冲均重复放电,即放电处于单倍周期放电模式,简称P1放电.图2a表明正脉冲放电峰值大于负脉冲放电,但是脉冲宽度要小于负脉冲放电,该结果与实验测量结果吻合[20].正负脉冲不对称的原因可以归咎为2个电极结构的不对称.对于负脉冲放电,瞬时阴极位于曲率较大的内电极,尽管没有考虑二次电子发射过程,但是边界处给定的恒定电子密度提供了一定的种子电子,从而维持强局域电场引发的电晕放电,使得击穿电压减小,如图2b所示,进而放电削弱,放电电流减小.此外,击穿电压的降低还导致电子迁移速度的降低,因而电流脉冲宽度增大.
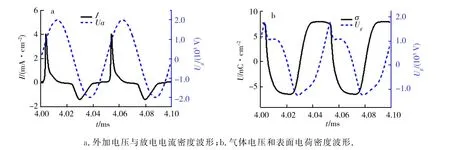
图2 单倍周期放电下的伏安特性曲线以及气隙电压和表面电荷密度的时间曲线Fig.2 Voltage-current waveforms and gas gap voltage and surface charge density waveforms in the single-period discharge
为获得这2次放电的放电模式,图3a和图3b分别给出了正脉冲和负脉冲峰值时刻电子离子密度以及电场的空间分布情况.在这2次放电中均出现了阴极区和准中性等离子体区(正柱区),这表明这2次放电均处于辉光放电模式.与平板型放电不同,同轴介质阻挡辉光放电具有独特的性质.在正电流脉冲峰值时刻,电子密度和离子密度在正柱区内向着阳极方向增长,最大电子离子密度出现在阳极附近,如图3a.尽管负电流脉冲低于正电流脉冲,但是其阴极鞘层厚度要低,并且其最大电场强度要高于正脉冲,如图3b所示.
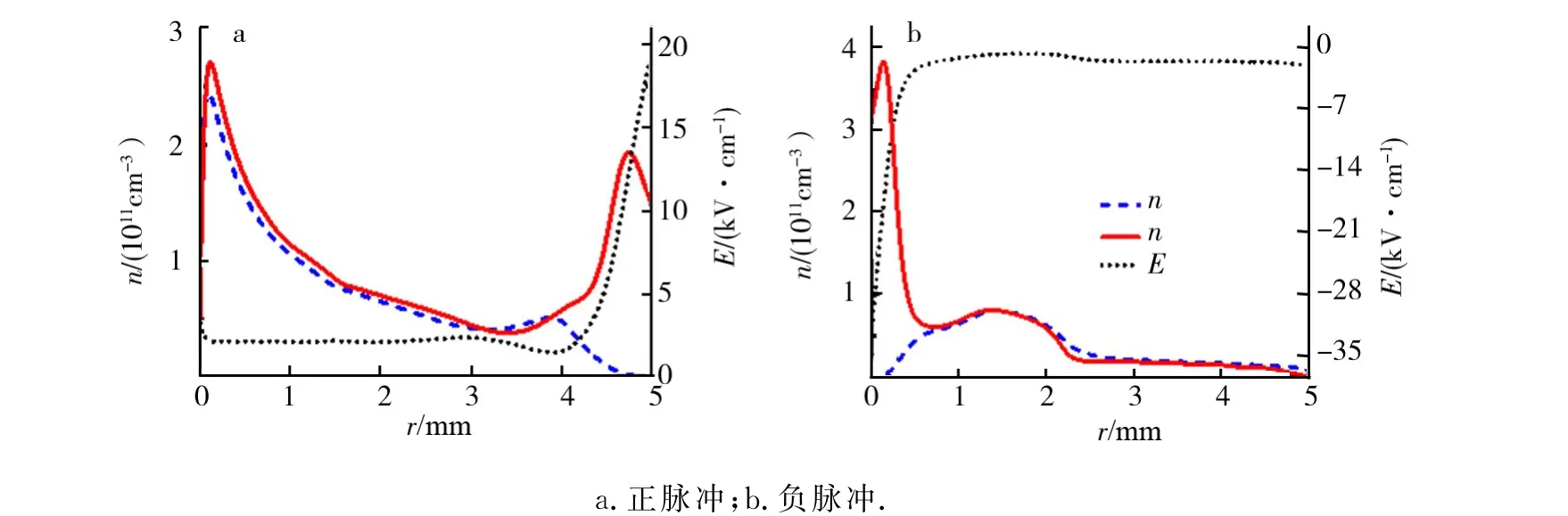
图3 单倍周期放电中电流峰值时刻电子离子密度以及电场的空间分布Fig.3 Spatial distribution of electron density,ion density and electric field at current peaks in the single-period discharge
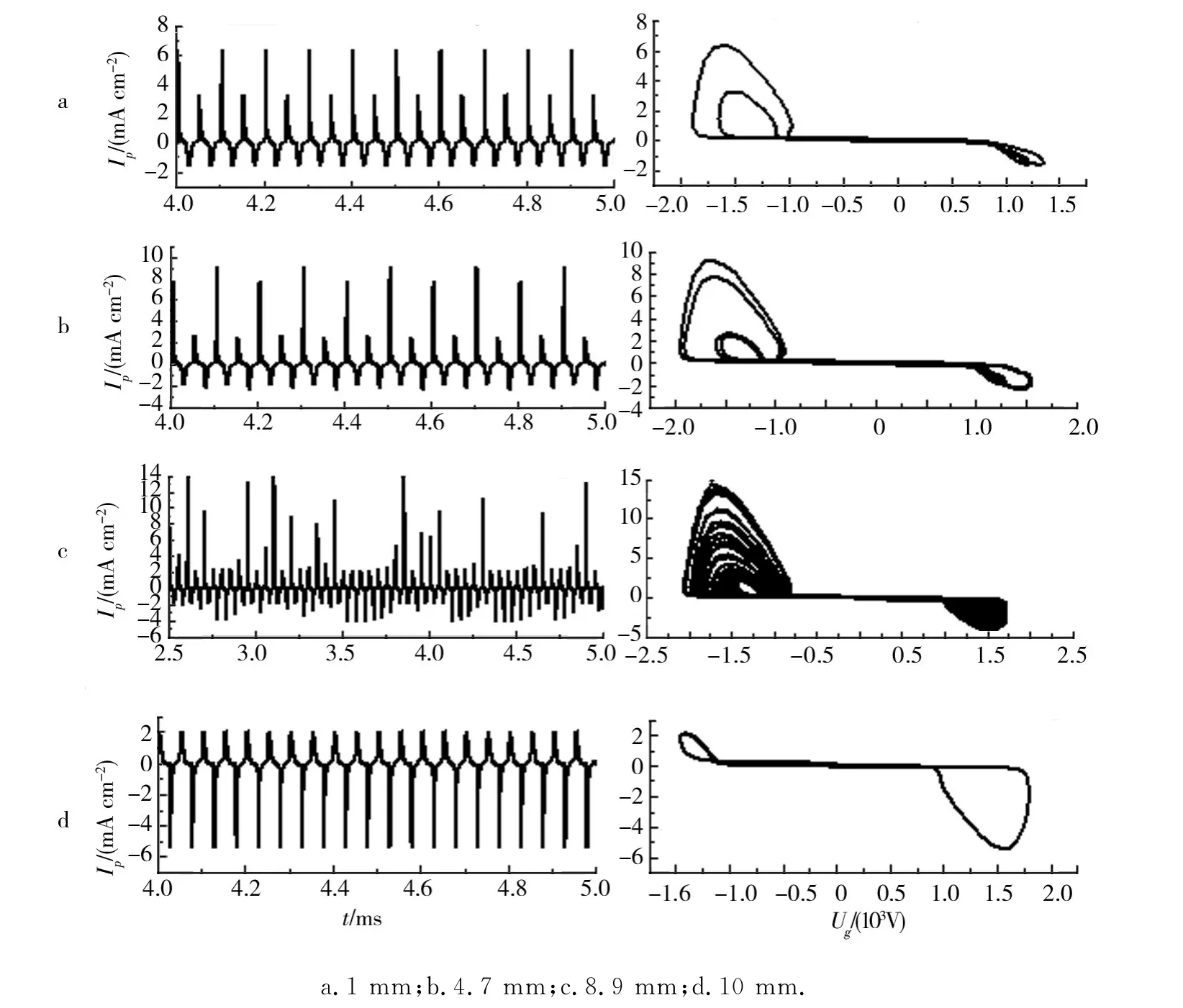
图4 不同电极半径R 下的放电电流密度波形图及其相应的相轨迹Fig.4 Time evolutions of current densities and their corresponding phase plots at different electrode radius R
保持其他放电参数不变,以内电极半径R作为控制参量.通过改变R的大小来研究电极曲率对放电的影响.诚然,随着内电极半径R的变化,R1与R2也会随之发生改变,三者曲率共同对放电产生影响,而内电极曲率较大,因此内电极曲率对放电产生的非线性行为起着主导作用.图4给出了内电极半径R分别为1、4.7、8.9、10 mm 时的放电电流图,以及与之对应的相轨迹图.其中,一个放电脉冲与一个极限环相对应.随着内电极半径R的不同,正负电流脉冲的大小均随之改变,由于负脉冲电流的变化相对较小,图5仅给出了正电流脉冲的峰值随内电极半径R的变化曲线图.从图5中可以看到,单倍周期放电(P1)只存在一个很窄的范围,增加半径R或者减小半径R放电都转变为双倍周期的放电(记为P2放电),如图4a所示.这意味着放电经历了一次倍周期分叉过程.在双倍周期放电中,放电电流在相邻的2个外加周期内的大小是不一致的,而且是交替出现的,即每经过2个外加周期才重复一次.在相空间内,其轨迹图对应着2个极限环.对于正放电脉冲,一个大的极限环内包含着一个小的极限环,但是对于负放电脉冲,这2个极限环并不是一个包含另一个,而是相互并排在一起.增大R值,P2放电中的2个电流脉冲之间的差值也随着增大.当R值达到4.7 mm 时,放电再次经历一次倍周期分叉过程而进入一种4倍周期(记为P4放电)的放电状态,如图2b所示.在P4放电中,正负脉冲都具有4个电流峰值.在相空间中,对应着4个极限环,其规律跟前文一致.进一步增大R,放电可以经历一系列的倍周期分叉,而最终进入一个混沌状态,如图4c所示.在该放电状态下,正负脉冲的电流大小是随机分布的,其相空间轨迹呈现了一吸引子的结构,即时空混沌态.再次增大R,放电从原来的混沌态突然又转变为了一个单倍周期的放电,与前面的P1放电的对称性相反,该放电负脉冲电流要大于正脉冲电流,如图4d所示.此时电极半径比较大,电极曲率较小,放电趋向于传统的平板型放电.其中图2a与图4d中放电对称性相反的主要原因在于放电的非线性现象是放电系统内在影响与曲率半径的影响共同作用的结果,当半径较小时曲率较大,曲率对非线性放电的作用效果更明显;而半径较大时曲率较小,曲率对非线性放电的影响较小,此时的非线性放电行为是由放电系统的内在因素的影响引起的.
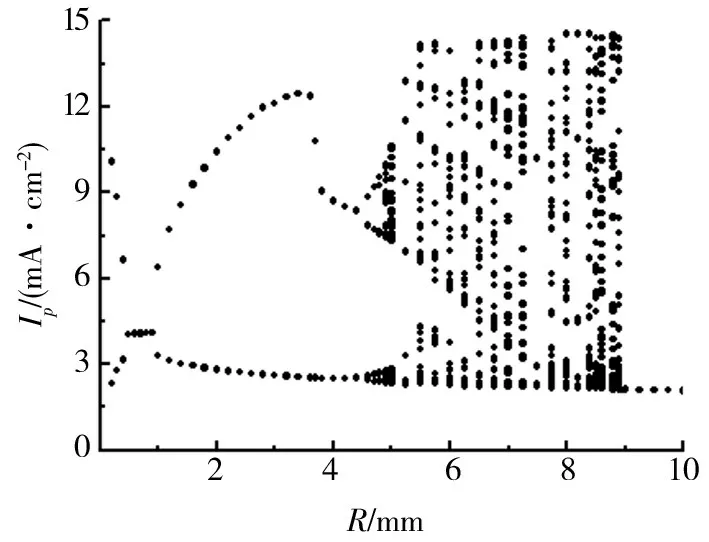
图5 正电流脉冲峰值随电极曲率半径R 的变化曲线Fig.5 Current peak of positive pulses as a function of the electrode radius R
为了弄清P1放电向P2放电转变的机理,将P2放电中2个连续正脉冲放电的击穿时刻的相关参数进行了对比研究,其中包括电子、离子的密度分布和空间电场的分布,如图6所示.图6a和图6b分别对应着大电流脉冲和小电流脉冲,显然这2次放电在击穿时刻电子和离子依然具有很高的密度值,达到1010cm-3数量级,且在空间中非均匀分布.由此可知,上一周期较强的正脉冲放电结束后遗留在空间的带电粒子较多,削弱了后续的负脉冲放电,而在下一次正放电之前带电粒子还没有完全消散,所以对于下一次正放电来说,种子电荷量仍然较大,预电离水平较高,随着外加电压的升高气体更易击穿,击穿电压降低,从而空间电场减小,并且更多的电荷积累在介质层表面,产生的反向电场逐渐增强,进一步使空间电场的发展受到限制,使得电流发展不成熟,最终产生中等强度的正脉冲,这种效应称为空间电荷的记忆效应.因此,较强的正脉冲和中等强度的正脉冲在时域放电中交替出现,促进了P2的形成.并且通过对比图6a和图6b可以发现,残余电荷越多,对下次放电影响越大,空间电场越低,放电越弱,电流越小.
值得说明的是,放电从开始击穿到稳定的P2放电状态所需要的时间跟内电极半径R偏离临界点(也叫分岔点)的程度有关.这里R2=0.89 mm 是指P1放电转变为P2放电的临界点.偏离程度越高,需要的时间越少,偏离越小,需要的时间越长.图7给出了R分别为0.5、0.9、1 mm 时正脉冲电流峰值在不同周期下的时间变化图.从图7中可以看到,当R=0.5 mm 时,放电从最初的扰动状态,大约经过20多个周期后转变为稳定的P1放电模式,即放电对扰动是稳定的.而当R为0.9 mm,即刚超越临界点时,系统经历了大约80个周期后,进入P2放电模式,且2个放电电流脉冲的峰值大小相差很小.当R=1 mm 时,此时系统已经远离了初次倍周期分叉,所以仅在几个放电周期后便进入了稳定的P2放电模式.

图6 双倍周期放电中2次正脉冲击穿时刻电子离子密度以及电场的空间分布Fig.6 Spatial distribution of electron density,ion density and electric field at breakdown in the double-period discharge

图7 不同电极半径R 下正电流脉冲峰值随着驱动周期的变化关系Fig.7 Current peak of positive pulses as a function of the driving period at different electrode radius R
3 结论
通过一维等离子体流体模型,以电极曲率半径为控制参量,数值研究了电极曲率对同轴型介质阻挡放电非线性行为的影响.模拟结果表明电极曲率是影响同轴介质阻挡非线性行为的一个重要因素.单倍周期放电只能出现在一定的曲率范围内,且无论是正脉冲放电还是负脉冲放电均处于辉光放电模式.随着电极半径的增大,放电经历一系列的倍周期分岔过程进入混沌态,然后突变为另一种形式的单倍周期放电.研究表明上一次放电产生的空间电荷引起的记忆效应是造成倍周期分岔的主要原因.此外,放电从击穿到稳定放电所需要的时间与系统偏离临界点的距离成反比.

