基于UWB的三维定位和优化滤波方法

李楠梁冰

(1.华北科技学院 机电工程学院,河北 廊坊 065201；2.华北科技学院 电子信息工程学院,河北 廊坊 065201)

GPS定位系统在汽车、船舶、飞机等室外运动物体的定位和导航具有广泛应用.但GPS定位系统的不足之处在于定位信号到达地面较弱以及不能穿透建筑物等.因此出现了一种新型的无线通信技术,即超宽带(ultra wide band,UWB)技术.该技术具有发射信号功率谱密度低、抗多径、安全系数高、系统复杂度低、传输速率高和穿透能力强等特点.从而使得超宽带技术引起极大的关注,近年来该技术被广泛应用于静止或者移动物体以及人的定位和跟踪[1-2].

基于UWB的三维定位算法设计与实现可用于无人机和室内机器人等领域.故近几年来国内外对UWB应用研究都十分热门,主要用于通信、雷达以及精确定位[4-6].文献[7]针对室内三维定位结果准确性的要求,提出了一种基于图优化的室内超宽带定位算法.文献[8]为解决基于MEMS的微惯性导航系统误差随时间发散、航向角发散快的问题,提出了一种利用UWB辅助修正惯性导航系统,实现室内较高精度定位的方法.文献[9]针对自主跟随机器人定位精度低的问题,采用飞行时间测距法,设计一种基于UWB的自主跟随机器人定位系统,实现机器人与跟随目标之间的高精度测距.

因为UWB可以获得三维空间2点间精确距离以及三边测量法(Trilateration)易于实现[10-15],故本文采用基于Python语言实现室内三维定位和优化滤波,为室内四旋翼飞行器室内定位选择适合的定位方案.本文使用的UWB 技术提供三维空间坐标定位信息的设备由4个锚点和无线UWB移动漫游器组成.在三维空间中(即x、y、z轴)设定4个固定锚点,移动的物体携带无线UWB 移动漫游器,通过其到4个固定锚点的距离即可确定出此刻自身所在三维空间的精确坐标.

1 三维定位的三边测量法

在三维空间中建立x、y、z3个坐标轴,此时空间中所有的点都可以用三维坐标(x,y,z)来表示,在空间中的某一平面内任取3个点,而后在该平面外再取1个点,以这4个点为圆心画球,可以得出1个公共交点,这4个随意取的点就是锚点.

三边测量法是一种常用的定位算法,在平面中先找到3个锚点,以它们为圆心作圆,可以得到唯一的1个交点,需满足以下2个条件:

1)已知3点位置 (x1,y1),(x2,y2),(x3,y3)；

2)已知未知点 (x0,y0) 到3点距离分别为d1,d2,d3.

以d1,d2,d3为半径作3个圆,根据毕达哥拉斯定理,得出交点即未知点的位置,计算公式为

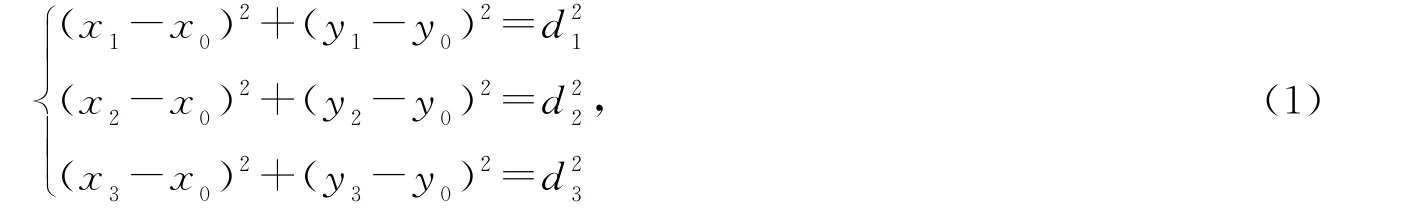
式(1)可通过图1进行表示.

在上面所列举的平面中的定位算法的基础上,可推广出三维空间定位法.在空间中的某一平面内任取3个点,以这3个点为圆心画球,可以得出2个公共交点,然后在该平面外任取1点,以其为圆心画球,可以确定出唯一的交点,故其条件可改为

1)已知4 点位置 (x1,y1,z1),(x2,y2,z2),(x3,y3,z3),(x4,y4,z4)；

2)已知未知点 (x0,y0,z0) 到4点距离分别为d1,d2,d3,d4.

以d1,d2,d3,d4为半径作4个圆,根据二维向三维的扩展,得出未知点的位置计算公式为

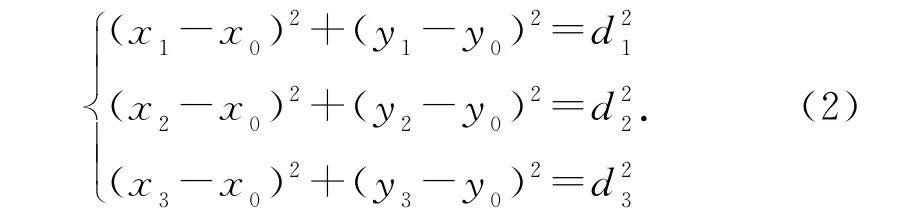
图1 三边测量法的二维平面原理Fig.1 Two dimensional plane schematic diagram of Trilateration method

通过式(2),可求出三维空间中的未知点.

2 三维定位的优化滤波法

通过三维定位的三边测量法测得坐标数值存在一定的误差,需对这些坐标数值进行优化滤波,获得更精确的坐标数据.常用的优化滤波方法主要有卡尔曼滤波法、平滑滤波、中值滤波和曲线拟合法等.

2.1 卡尔曼滤波

假设系统的离散状态方程为

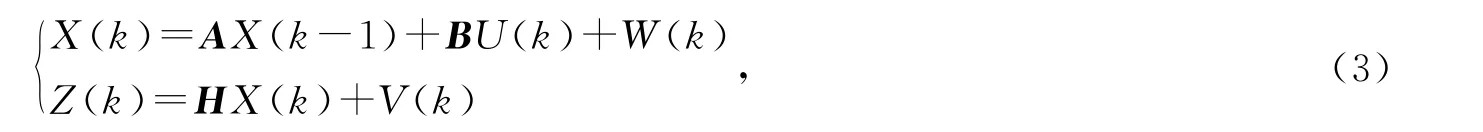
式(3)中,A和B是系统参数矩阵,H是系统测量矩阵,X(k)是k时刻的系统状态,U(k)是k时刻对系统的控制量,Z(k)是k时刻的测量值,W(k)和V(k)分别表示过程噪声和测量噪声.

根据系统的模型,可以根据系统的上一状态而预测出现在状态:

式(4)中,X(k|k-1)是利用上一状态预测的结果,X(k-1|k-1)是上一状态最优的结果,U(k)为现在状态的控制量,可以为0.

此时,系统结果已经更新,但对应于X(k|k-1)的协方差还没更新,协方差P为

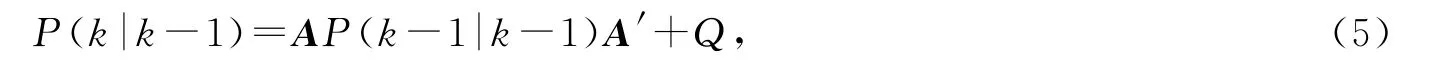
式(5)中,P(k|k-1)是X(k|k-1)对应的协方差,P(k-1|k-1)是X(k-1|k-1)对应协方差,Q是系统过程的协方差,A′表示A的转置矩阵.式(4)和(5)就是对系统状态的预测.

可得现在状态(k)的最优估算值X(k|k):

式(6)中,Kg为卡尔曼增益,其公式如下:

要使卡尔曼滤波不断运行下去直到系统过程结束,还需要更新k状态下X(k/k)的协方差,

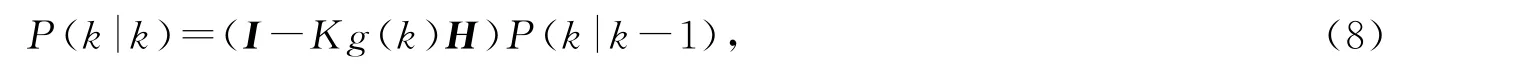
式(8)中,I是值为1的矩阵.当系统进入k+1状态时,P(k|k)就是式(5)中的P(k-1|k-1).算法就可以自回归的运算下去.

上文中的式(4)～(8)是卡尔曼滤波的5个基本公式,可用图2来表示.

图2 卡尔曼滤波器的工作原理Fig.2 Working principle of Kalman filter

2.2 平滑滤波

空间域中的平滑滤波一般是采用简单平均法进行,也可以说是均值滤波,例如,一序列{0,3,4,0,7},此列若用平滑滤波,窗口取5,那么平滑滤波输出为(0+3+4+0+7)/5=2.8.其公式可表示为

其中,S为模板,M为该模板中包含当前坐标在内的坐标总数.

2.3 中值滤波

中值滤波就是用一个移动窗口,将窗口的中心点的值用窗口内的各点中值代替.假设窗口内有5点,其值为80、90、200、110和120,那么此窗口内各点的中值为110.

设一维序列为x1,x2,x3,…,xn,取点数为n,对其进行中值滤波,就是从输入序列中相继抽出n个数.

把1个点的特定长度或形状的邻域称作窗口.在一维情况下,中值滤波器是一个含有奇数个点的滑动窗口.中值滤波很容易推广到二维,此时可以利用二维形式的窗口.

2.4 曲线拟合

由于室内多移动机器人系统运行环境处于室内,故利用设计的UWB模块实测了已知真实距离的50组数据,然后通过曲线拟合,得到其近似变化规律.本文曲线拟合以最小二乘法为基础,选用冥函数{1,x,x2,…,xn}作为函数类,则

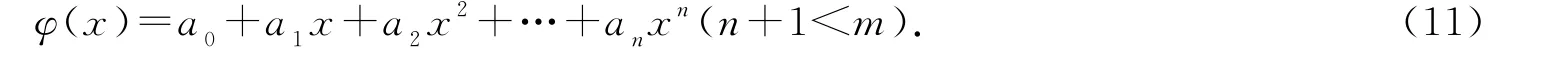
这就是拟合函数.为了确定该拟合函数的系数,需要求解正规方程组

解得a0,a1,…,an即可,将其代入

可得到拟合后的函数.

3 基于UWB的三维定位与优化滤波的实验分析

表1给出了6种定位各项技术性能,无论是定位精度和可靠性,还是使用成本和安全性,UWB 技术相比与其他的室内定位技术都占有很大的优势.综合考虑本实验将选用UWB技术在室内完成.

表1 室内定位技术对比Tab.1 Comparison of indoor positioning technology

3.1 硬件环境

超宽带在本次实验中采用的硬件由4个锚点和UWB漫游器等诸多元器件组成,表2是实验硬件列表,图3是UWB锚点.

表2 Trek 1 000的硬件组成Tab.2 Hardware composition of trek 1 000

3.2 基于UWB的三维空间定位实验

在实验中,4个锚点分置于1个正方体8个顶点的其中4个上,所需定位的物体(如四旋翼无人机等)携带tag(即UWB漫游器),如此实现定位,如图4所示.

图3 实验中的UWB锚点Fig.3 UWB anchor point in the experiment

图4 测量的系统空间样式Fig.4 Measured system space style

运行如下循环赋值语句,赋予变量一些随机的初值

在赋值完成后,可以通过运行Python软件中的IDLE来进行检测,看是否能获得大量随机数据.程序编写主要完成Python串口程序、三维空间定位程序、多种优化滤波程序等的编写工作.通过UWB技术进行数据采集,主要是采集4个锚点到需测点的距离d1、d2、d3、d4,并将其过串口连接程序输入到三维定位算法的程序中,经过计算,得到未知点的坐标,由于实验误差,未知点的坐标会在一片范围内波动,此时采用优化滤波的程序,减小波动的范围,完成实验.

在该程序中,选取了

这4个锚点在长宽高都为1的正方体的顶点上,设未知点 (x0,y0,z0) 处于正方体的中心,则到4点距离分别为

最终经过程序的计算定位得到未知点的坐标为(0.5,0.5,0.5),该点刚好位于正方体的中心,由此证明此程序的正确性.

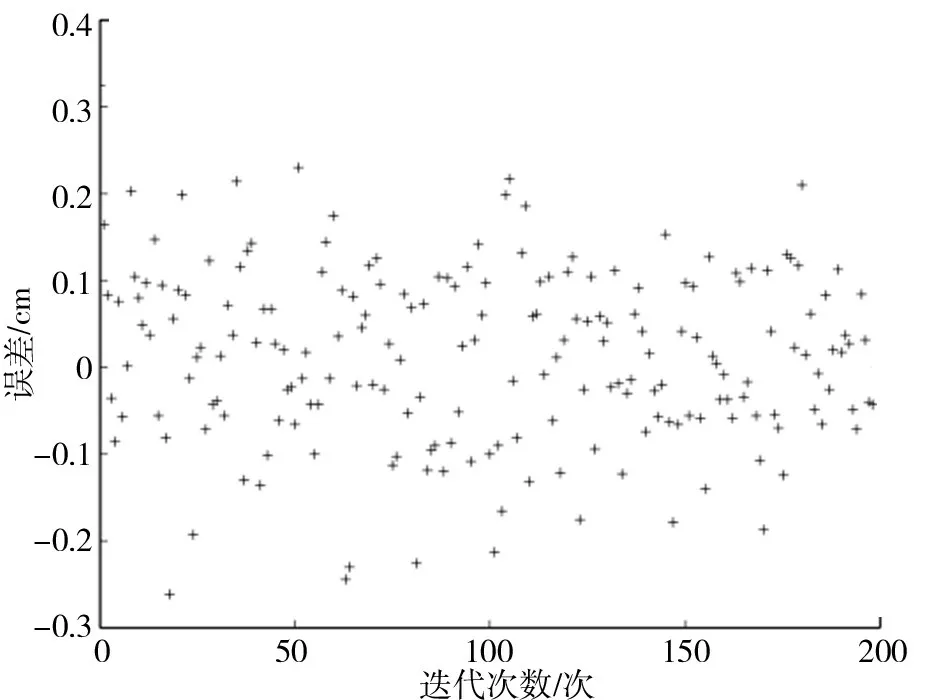
图5 测量所得数据Fig.5 Measured data

实验通过测量四旋翼无人飞行器的三维空间坐标证明所编写的算法是可以实现的,利用四旋翼无人飞行器进行的实验过程.电脑程序输出的一部分坐标值见图5.实验得到众多三维空间坐标,大范围是一致的,但也存在一些误差波动,图5是实验测量得到三维坐标换算成的数学数值,利用了相减而后求均值的方法,下面的优化滤波都是对这些数值进行的.

滤波是指利用一定的手段抑制无用信号,增强有用信号的数字信号处理过程.优化滤波是本设计的主要内容之一,如果没有优化滤波,测得的三维空间坐标就会存在很大的误差,经过滤波的数据可以使得定位更加精确.扩展卡尔曼滤波算法原理图如图6所示.

在本设计中,三维定位算法计算得到的大范围坐标数据输入卡尔曼滤波程序中,经过筛选,留下小范围内的坐标.上述三维空间定位算法采用了矩阵的形式,此处卡尔曼滤波也使用相同的方法.将得到的坐标换算成数值进行4种优化滤波:卡尔曼滤波、平滑滤波、中值滤波、曲线拟合.运行优化滤波程序,可得如图7～11的5幅优化滤波后的曲线或折线图.

图6 扩展卡尔曼滤波算法原理图Fig.6 Schematic diagram of extended Kalman filter algorithm

图7 卡尔曼滤波Fig.7 Kalman filtering

图8 卡尔曼滤波方差Fig.8 Kalman filter variance

图9 平滑滤波Fig.9 Smooth filtering

图10 中值滤波Fig.10 Median Filtering

图11 曲线拟合Fig.11 Curve Fitting

对测得的空间坐标进行优化滤波,表3给出了4种滤波方法的性能比较.通过表格的对比,可以看出,卡尔曼滤波程序运行速度是第二高,而且其对环境的需求不是特别高,其性价比和精度很高,相比较于其他3种滤波,卡尔曼滤波是本次实验所得到的最优选择.

表3 4种滤波对比表格Tab.3 Four filter comparison tables

3.3 实验结论

本实验主要完成基于超宽带的三维空间定位,同时对坐标进行优化.实验环境为有书桌、椅子和柜子的实验室,2 m×2 m×2 m 的无障碍区域.利用超宽带技术测距,而后经过三维空间定位算法的程序得出概略坐标,最后由优化滤波完成实验,最终确定优化滤波方案是卡尔曼滤波.

4 结论

超宽带技术目前是一种主流的定位技术,其具有发射信号功率谱密度低、抗多径、安全系数高、系统复杂度低、传输速率高和穿透能力强等特点.本文给出了一种基于超宽带的三维定位算法,并对获得三维空间的坐标数据进行优化滤波比较,确定了室内4旋翼飞行器定位的卡尔曼滤波方案.实验结果表明,本文所提出的基于超宽带的三维定位和优化滤波方法是有效的.