基于连续动态时间规整算法的工业机器人轨迹准确度分析

李 睿，王炳荣，崔晓玲

（北京工业大学北京市精密测控技术与仪器工程技术研究中心，北京100124）

1 引 言

工业机器人是智能制造的关键装备之一，随着工业机器人在精密制造、航空航天、精密测量等高精度领域应用的不断增加，对机器人的运动性能要求也越来越高［1］。机器人轨迹准确度和重复性指标是衡量机器人性能最关键的指标之一，国际标准ISO 9283（Manipulating industrial robots-Performance criteria and related test methods）［2］，国标GB/T 12642-2003：工业机器人性能规范及其试验方法［3］，欧洲工业机器人标准改进项目［4］（IRIS）以及美国国家标准ANSI/RIA R15.05-2-1992：Path-Related and Dynamic Performance Characteristics Evaluation［5］，均对机器人轨迹准确度和重复性测试方法进行了定义。

目前，以上3 个标准广泛被应用于工业机器人轨迹性能测试中。根据国际标准ISO 9283 中对位姿精度的试验规范和要求，韩国机器人工业发展研究所采用激光跟踪测量系统［5］对工业机器人进行基于D-H 模型的运动学参数标定；天津大学采用双目视觉系统［6］对工业机器人进行了位置误差标定。北京工业大学在国标GB/T 12642-2013 的基础上，分析工业机器人每一项运动性能的定义和物理意义并开发了一套性能测试与评价软件［7］。伊朗科技大学基于美国ANSI/RIA R15.05-2-1992 标准开发了一套基于视觉的工业机器人控制系统，完成了对工业机器人的轨迹性能测试［8］。

ISO 9283 和GB/T 12642 标准中，规定需构造垂直于指令轨迹的法平面，与实际轨迹相交计算轨迹准确度，并制定了试验方法，但标准中没有具体规定法平面构造的位置，仅说明选择时应与测量形状和速度相关。ANSI/RIA 中规定在指令轨迹上等距构造法平面，然而对于非直线轨迹，受机器人的运动速度和运动偏差、测量系统的采样频率和测量误差的影响，轨迹上各点法线不断变化，构造的法平面可能相交，导致指令轨迹与实际轨迹点之间产生错误的映射，造成较大的测量误差。

针对非直线轨迹法平面构造时，受机器人运动速度和运动偏差、测量系统的采样频率和测量误差的影响，导致指令轨迹与实际轨迹点之间出现映射错误，造成较大的轨迹测量误差的问题，本文提出了采用连续动态时间规整算法（Continuous Dynamic Time Warping，CDTW）解决机器人轨迹映射的问题，通过对工业机器人轨迹准确度进行测量分析，与国际标准ISO 9283 中的评价方法进行对比，并着重分析了机器人运动速度以及测量系统采样频率对轨迹映射方法的影响，验证了动态时间规整方法（Dynamic Time Warping，DTW）应用于轨迹准确度分析的有效性和正确性。

2 机器人运动特性的测试评价方法及问题分析

国际标准ISO 9283 中规定，工业机器人轨迹准确度由指令轨迹的位置与各实到轨迹位置集群中心线之间的偏差决定，如图1 所示。

沿指令轨迹选择m个点并计算其法平面，n条实测轨迹与法平面交点坐标的平均值与指令轨迹的距离的最大值ATP为位置轨迹准确度：

图1 ISO 标准的轨迹准确度Fig.1 Path accuracy of ISO standard

美国标准ANSI/RIA R15.05-2-1992 与ISO 9283 的轨迹准确度试验标准相类似，规定了法平面的放置位置，如图2 所示。标准规定指令轨迹必须是二维的，位于标准测试平面XOY上，此标准测试平面为参考平面，取决于机器人的工作空间，L为标准测试平面的宽度。法平面与标准测试平面法线对齐，并在参考轨迹上等距放置。通过法平面与指令轨迹和实测轨迹的交点来计算轨迹误差。然而在非直线轨迹的情况下，法平面仍然会交叉并使时间序列颠倒，造成轨迹点之间的错误映射，并且此法平面的构造放置方式无法对尖锐拐角点进行映射。

图2 美国标准的轨迹准确度Fig.2 Path accuracy of ANSI

欧洲机器人工业标准改进项目（IRIS）规定在实测轨迹的每个采样点处构造与轨迹切线垂直的法平面。但该方法在轨迹较为复杂的情况下仍然存在局限性，受机器人运动偏差和测量误差影响，实测轨迹的切线具有不确定性，法平面可能相交，导致时间顺序颠倒，造成错误的映射，如图3 所示。图3（a）为直线轨迹，由于运动偏差或测量误差的影响，采样点处的法平面可能相交，导致映射的错误，造成微小的轨迹测量误差。图3（b）为拐角轨迹，为保证运动的连续平稳，机器人在拐角处的运动轨迹为近似轨迹，实测轨迹的形状与指令轨迹在拐角处存在一定的偏差，导致明显的映射错误，造成较大的轨迹测量误差。图3（c）为一个实际的例子，可以看到，拐角处实测轨迹为接近过渡方式，在拐角处实测轨迹采样点的法平面与指令轨迹相交于明显错误的位置甚至不相交，造成极大的轨迹测量误差，在拐角轨迹与直线轨迹的相交处容易发生图3（a）所示的映射错误。

图3 切线法平面存在的映射问题Fig.3 Problem of tangent normal plane

工业机器人在空间中的运动轨迹可以看作时间的函数，其轨迹数据可以看作一条时间序列。DTW 算法是一种衡量两个时间序列相似度的方法，用满足一定条件的时间规整函数描述两者之间的时间对应关系，实现两序列间的最优匹配。因此，针对指令轨迹与实际轨迹采样点之间的映射关系问题，采用DTW 算法进行研究分析。

3 动态时间规整

DTW 算法是一种具有非线性时间归一化效果的模式匹配算法［10］，在工业机器人的运动轨迹分析中，本文利用这种算法进行工业机器人实际轨迹与指令轨迹之间的映射，避免出现映射后时间顺序颠倒的问题。

3.1 DTW 算法

DTW 算法是一种把时间规整和距离测度计算结合起来的非线性规整技术［11］，通过不断地计算两矢量间的距离来搜索两者之间最优匹配路径，保证它们之间存在最大的相似度。该算法原理如下：

定义两个离散序列：则，两个离散序列中各点xi和yj之间的距离：

定义两者的相似性度量函数D(i，j)，即两条序列之间的累积距离：

定义规整路径ω，将序列Y上的数据点非线性地映射到序列X上，使得两者的累积距离最小：

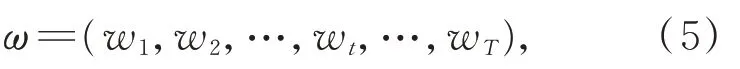
其中：wT=D(i，j)，ωT是规整路径ω上的第T个元素，表示xi与yj建立的对应关系。

回溯法［12］是一种选优搜索方法，按选优策略向前搜索，以达到目标，本文选用回溯法得到规整路径ω。规定规整路径ω的回溯优选策略为：

（1）边界性：规整路径ω要从点(xm，yn)开始，到点(x1，y1)结束；

（2）单调连续性：规整路径ω从点(xm，yn)开始，只能去往(xm，yn-1)或(xm-1，yn)或(xm-1，yn-1)。

通过上述约束条件可以找到一条累积距离最小的规整路径，此时序列X和Y之间即可实现最优匹配。采用动态时间规整算法对两条二维轨迹进行映射分析，结果如图4 所示。图4（a）的坐标轴分别表示两条轨迹的采样点，网格表示两条轨迹全部采样点之间的所有可能映射，每个网格点的数值代表两点间的相似度量值，通过回溯法的优选策略得到最优规整路径，根据序列间的规整路径得到图4（b）中两条轨迹的映射关系。

图4 动态时间规整算法的轨迹映射示例Fig.4 Path mapping example of DTW

3.2 CDTW 算法

将DTW 算法应用于机器人运动分析的一个主要缺点是映射的离散化［13］。机器人在运动时的轨迹是连续的，但轨迹测量数据是离散的，离散的数据导致在应用DTW 算法进行轨迹映射时只能映射到已有的数据点，这种匹配导致两条轨迹间的相似性度量值增大，点与点之间的匹配度降低，可能出现数据点之间多对一的情况。当采样频率较小时，这种现象更加明显。

CDTW 算法的目标是找到最佳的连续规整路径，即规整路径不再被约束为通过图中的节点，可以映射到两个连续数据点之间的插值点［14］。不同映射方法获得的规整路径对比如图5所示。

图5 DTW 与CDTW 映射对比Fig.5 Mapping comparison between DTW and CDTW

与DTW 算法的回溯优选策略不同，CDTW算法的连续性不再局限于网格上的节点，路径匹配规则如图6 所示。图6（a）为采用DTW 算法，规定规整路径ω只能去往3 个边界点，图6（b）为采用CDTW 算法，规整路径ω可以到达网格的左方和下方中行列之间的插值点。

图6 DTW 与CDTW 路径匹配规则对比Fig.6 Comparison of Path matching rule between DTW and CDTW

因此，两序列之间的相似性度量函数表示如式（6）所示：

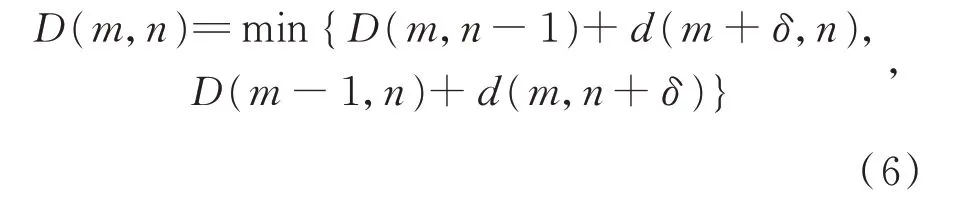
其中，δ为介于0～1 之间的一个参数。δ非零时，一条轨迹的对应点必定位于另一条轨迹上的插值点，可以通过线性插值模型计算具体位置［15］。对于两条待映射的轨迹曲线C1和C2，通过弧长参数化来描述线性插值模型，曲线上的插值点分别对应r1和r2，如图7 所示。

图7 曲线参数化Fig.7 Curve parameterization

曲线C1和C2的点坐标方程式Ck为：

其中：

通过确定r1，r2即可获得插值点的具体位置。当CDTW 算法进行回溯时，相似性度量矩阵D(i，j)中如果出现多点映射一点的情况，通过线性插值模型在多对一映射的数据点之间进行插值，直到数据点间实现一一映射。通过CDTW算法得到的规整路径更平滑，能够更好的反映测量轨迹与指令轨迹点之间的映射关系。机器人在执行拐角轨迹过程中速度会发生变化，因此在数据点相较稀疏的区域进行选择性的插值处理来提高算法的精度。

4 机器人运动轨迹测量

本文采用Leica 激光跟踪仪对KUKA KR6 R700 工业机器人进行轨迹测量实验，参照ISO 9283 标准中提供的可选用的试验轨迹规划机器人运动轨迹，试验装置如图8 所示。

图8 试验装置图Fig.8 Test device

机器人的实际轨迹为时间的函数，因此与其对应的理论轨迹也应该是与时间相关的一条轨迹数据点，而非等间隔采样的数据。根据在示教器上输入的指令轨迹，机器人系统生成一条理论轨迹点，该理论轨迹是时间的函数，可以通过上位机与机器人通信实时获得理论轨迹数据。机器人的运动控制是由机器人的内部控制环境KRL（KUKA Robot Language）与RSI（Robot Sensor Interface）来实现的，KRL 是机器人控制编程接口，主要对实现机器人的非实时控制，在KRL 环境中编写运动轨迹程序。RSI 是机器人通信接口，实现与外部系统进行数据交互，通过上位机编程对RSI 对象进行配置和调用便可实现机器人运动数据的获取。本文通过RSI 读取机器人理论轨迹，通过外部测量设备激光跟踪仪测量机器人的实际轨迹。

4.1 机器人通信

RSI 可通过Ethernet 通信或机器人总线IO与外部系统实现数据交互，具备周期性的信号处理和评估能力。RSI 每隔12 ms 进行一次数据交互，实时性较好。上位机与机器人控制器进行的数据交换是以XML 格式进行的，通信前的参数配置如图9 所示。

图9 XML 文件配置Fig.9 XML file configuration

RSI 上下文是在KRL 程序中被加载的，其对信号的处理与KRL 程序并行执行，并可按需要激活或取消激活。RSI 在KRL 程序中调用的流程为：声明KRL 变量，创建RSI 上下文，将配置的参数加载到RSI 容器中。激活RSI，上位机建立与机器人系统的通信，机器人执行运动轨迹，上位机周期性的获取机器人的实时数据，轨迹执行结束后关闭RSI。

4.2 机器人与激光跟踪仪坐标系变换矩阵标定

机器人基坐标系和测量坐标系的转换可以通过测量机器人安装平面及轴1，2 轴线拟合计算，但机器人运动学参数误差会影响坐标系转换的准确性，因此本文采用D-H 模型对机器人运动学参数进行标定［16］，利用标定后的参数精标定坐标系转换矩阵，提高测量精度。

利用激光跟踪仪获得机器人末端靶标位置，采用位置误差最小模型解算机器人的运动学参数，以测量的位置与实际位置之间的差值最小为约束条件来求解参数，坐标系转换关系如图10所示。

图10 坐标系转换关系Fig.10 Coordinate system conversion

激光跟踪仪与机器人坐标系转换存在3 个旋转误差δx，δy，δz以及3 个平移误差dx，dy，dz。两坐标系的转换矩阵误差可由如式（8）表示：

将靶球刚性连接在机器人末端，相对于末端只发生了平移变换，误差关系式为：

建立测量得到的靶球坐标系Otm与计算得到的靶球坐标系Otc的关系式：

至少选取测量11 个位置坐标用于标定，并利用最小二乘法进行求解。标定后机器人的坐标系转换矩阵误差及靶球安装误差如表1所示。

表1 坐标系转换矩阵误差及靶球安装误差Tab.1 Coordinate system transformation matrix error and target ball installation error（mm）

5 机器人轨迹准确度试验

根据ISO 9283 标准附录中的可选测试轨迹数据集编辑一条轨迹，该轨迹位于标准测试平面内，包括直线、圆弧和拐角运动的组合。机器人首先执行一段直线轨迹，起点P1坐标为（400，-50，750），P2为（450，-50，750）。其次执行一段圆弧类型的圆滑拐角，设置拐角为5 mm。最后执行一段直线轨迹，终点P3为（450，0，750）。上位机实时读取机器人系统的理论轨迹，激光跟踪仪读取机器人的实际运行轨迹，通过坐标系变换转换到同一坐标系下。

5.1 直线轨迹映射方法对比

为了比较ISO 标准规定方法、DTW 算法以及CDTW 算法的映射结果，设置激光跟踪仪采样频率为50 Hz，首先选取了直线轨迹处的30对数据点。采用ISO 标准方法和DTW 算法进行映射，轨迹映射对比分析如图11 所示，计算直线轨迹映射后的轨迹准确度结果如图12所示。

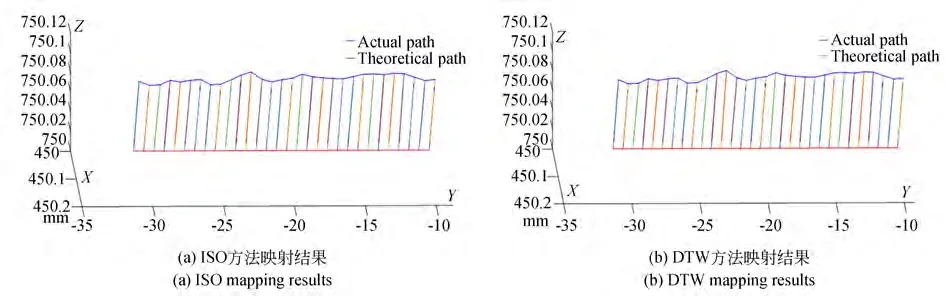
图11 直线轨迹映射结果Fig.11 Comparison of linear path mapping result

图12 直线轨迹准确度计算结果Fig.12 Calculation results of linear path accuracy

图11 中的直线轨迹，机器人的运行速度相对稳定，采样点比较均匀，ISO 方法获得的轨迹准确度为0.312 mm，DTW 算法获得的轨迹准确度为0.306 mm。轨迹准确定测量精度为0.01 mm，两种算法计算结果相差0.006 mm，相对误差1.9%，计算结果相一致，说明采用映射算法对轨迹准确度的计算结果是正确的。

5.2 拐角轨迹映射方法对比

选取拐角处的50 对数据点，采用3 种方法分别对两种轨迹的数据点进行映射。对于ISO 标准中的法平面放置问题，采用文献8 的方法优化。轨迹映射对比如图13 所示。

图13 拐角轨迹映射结果比较Fig.13 Comparison of corner path mapping result

图13 中可以看到，在机器人执行拐角轨迹时，受机器人运动速度以及机器人运动偏差的影响，导致实际轨迹的形状与指令轨迹存在一定的差别，图13（a）中的ISO 轨迹映射方法在点21 至点30 处的10 个点存在时间序列的失真，占轨迹总点数的20%，导致映射的错误，严重影响轨迹准确度评价的正确性。图13（b）中的DTW 算法则不会产生这种问题，能够正确地进行轨迹点之间的映射。但由于采样频率的限制，在理论轨迹点14，17，21，31，35，37 处存在非一一映射的现象，占总点数的12%，导致轨迹准确度的不准确。图13（c）中采用CDTW 算法不仅不会产生映射错误问题，由于内插点的存在，实际轨迹点能够映射到理论轨迹的非参考点上，不会出现一点映射多点的情况。计算拐角轨迹映射后的轨迹准确度结果如图14 所示。

图14 拐角轨迹准确度计算结果Fig.14 Calculation results of corner path accuracy

ISO 的方法测量得到的轨迹误差值大，与图13（a）对比分析可知，点21 至点30 的测量误差是由于ISO 方法的映射错误导致的。DTW 算法明显减小了映射后的轨迹准确度，与图13（b）对比分析可知，曲线的4 个峰值点是由于采样频率的限制导致数据点之间发生多对一的映射导致的。CDTW 算法通过内插点解决了此问题，误差曲线更光滑，提高了轨迹准确度。采用ISO 方法计算得到的轨迹准确度为1.343 mm，标准差为0.389 mm；采用DTW 算法计算得到的轨迹准确度为0.585 mm，标准差为0.194 mm；采用CDTW 算法计算得到的轨迹准确度为0.357 mm，标准差为0.054 mm。CDTW 算法映射后的轨迹准确度提高73%，标准差减小86%，误差整体波动幅度明显变小。

5.3 机器人运动速度对映射的影响

ISO 9283 中规定，机器人轨迹准确度的测试应与轨迹速度相关，因此选择机器人运行速度50%和100%，分析不同速度下DTW 和CDTW算法对测量精度的影响。选择激光跟踪仪采样频率保持50 Hz，获得两组轨迹数据，取得拐角处的57 对数据点和30 对数据点，代入DTW 算法和CDTW 算法，分析机器人运动速度对映射方法的影响。不同速度下DTW 算法和CDTW 算法的映射结果如图15 所示。

图15 不同速度下的DTW 算法和CDTW 算法的映射结果Fig.15 Mapping results of DTW and CDTW algorithm at different speeds

由图15 可知，由于机器人运动偏差的影响，机器人执行拐角运动时存在过冲和超调，速度越快机器人运动偏差越大，同时，相同采样频率下，运动速度越快采样点个数越少。对比50% 和100%速度下DTW 算法映射的结果，可以看到数据点映射时都会出现多对一的情况，但随着速度的降低，数据点的增加，数据点多对一的映射情况减少。对于50%和100%速度下的CDTW算法，由于CDTW 能够进行数据点之间的插值，因此不会受到数据点密度的影响。映射后的轨迹准确度对比分析如表2 所示。

表2 不同速度下的两种算法的轨迹误差对比Tab.2 Comparison of path error between DTW and CDTW algorithm at different speeds（mm）

由表2 可知，当速度相同时，CDTW 算法相比于DTW 算法轨迹准确度提高了40%。当速度降低时，CDTW 算法标准差减小54%，DTW算法标准差减小34%，CDTW 算法能够更好地降低误差整体波动幅度。

5.4 测量系统采样频率对映射的影响

为了分析测量系统的采样频率对映射的影响，设置激光跟踪仪采样频率分别为25 Hz，50 Hz 和80 Hz，获得两组轨迹数据，分别取得拐角处的20 对数据点、40 对数据点和68 对数据点，代入ISO 算法、DTW 算法和CDTW 算法，分析采样频率对3 种映射方法的影响。实验结果如表3所示。

采用ISO 算法进行轨迹间的映射，随着采样频率的增大，采样点之间的距离间隔变小，轨迹切线变得陡峭，出现映射错误的轨迹点增多。由表3 可知，当采样频率从25 Hz 增加到80 Hz 时，轨迹准确度从1.160 mm 降低到1.532 mm，标准差从0.304 mm 增大到0.535 mm。采样频率的提高导致ISO 算法映射后的轨迹准确度降低，误差整体波动幅度增大。

表3 不同频率下3 种算法的轨迹误差对比Tab.3 Comparison of path error of three algorithms at different frequencies（mm）

DTW 算法是点对点之间的映射，随着采样频率的提高，轨迹点密度增大，轨迹点之间能够更好地实现一对一的匹配。通过表3 则可以看出采用DTW 映射方法与ISO 映射方法正好相反，当采样频率从25 Hz 增加到80 Hz 时，轨迹准确度从0.678 mm 提高至0.508 mm，标准差从0.242 mm 减小至0.159 mm。采样频率的提高导致DTW 算法映射后的轨迹准确度提高，误差整体波动幅度减小。

对于表3 中的CDTW 算法映射轨迹误差，当采样频率从25 Hz 增加到80 Hz 时，轨迹准确度的极值为0.015 mm，标准差的极值为0.003 mm。由于CDTW 算法采用插值计算，采样频率不会对其轨迹准确度造成明显的影响。

6 结 论

本文提出了一种基于连续动态时间规整方法的工业机器人轨迹准确度分析方法，通过对两轨迹序列的相似度最优匹配进行映射，对采样数据点建立插值模型来提高轨迹点之间的映射准确度，解决了不同速度和复杂轨迹测量中由于映射错误导致的轨迹准确度评价不准确的问题。

采用激光跟踪仪测量机器人的运动轨迹，针对直线轨迹与拐角轨迹将该方法与ISO 标准方法进行对比分析，并分析了机器人运动速度和测量系统的采样频率对算法的影响。实验结果表明：ISO 标准方法和DTW 算法能够很好地应用在直线轨迹准确度评价中，对于拐角轨迹ISO 方法出现明显的映射错误，DTW 算法解决了映射错误，但受机器人运动速度和测量系统采样频率的影响存在多点映射的问题，CDTW 算法有效解决了此问题，提高了轨迹准确度。