数控机床稳健性温度敏感点的选择

刘昀晟，苗恩铭，张明德，冯 定，李建刚

（1. 合肥工业大学仪器科学与光电工程学院，安徽合肥230009；2. 重庆理工大学机械工程学院，重庆400054；3. 长江大学机械工程学院，湖北荆州434023；4. 哈尔滨工业大学（深圳），广东深圳518055）

1 引 言

热误差对数控机床尤其是高精度数控机床的精度影响严重，占总误差的40%～70%［2-3］。降低机床热误差对加工精度的负面影响成为研究热点。目前，减小热误差影响的方法主要有：结构的改进，新材料的使用，温度的控制、建模并以软件方式补偿热误差等。

以有限元法为代表的数值模拟方法被广泛应用于机床结构的热变形建模。邓小雷等人［4］对数控机床主轴-立柱系统进行了有限元分析，建立了主轴-立柱系统耦合分析模型来获取其热态特性。Li 等人［5］研究了热误差和力诱导误差对滚齿机加工精度的耦合影响，并在此基础上进行了数值模拟，揭示了组件和工作台的温度分布以及相应的位移误差。该方法可以在设计阶段完成机床整体或关键部件的尺寸优化，但是更适用于新的机床产品，因计算速率等问题，较难对现有机床进行在线实时热误差补偿。

Ge 等人［6］通过使用具有负线性膨胀系数的碳纤维增强塑料（Carbon Fiber Reinforced Plastic，CFRP）来补偿金属的热膨胀，采用结构拓扑设计方法设计了热变形补偿系统中的传热通道，使热量均匀分布。Grama 等人［7］从温度控制的角度提出了冷却器触发模型，通过动态控制冷却器压缩机的开关频率和开关“开启”时间，使散热与机床产生的热量相一致，大大降低了机床的热误差。然而，新材料的使用和温度控制这两种方法的补偿成本很高，而且属于在机床设计阶段的优化方法，不适合对现有机床进行热变形补偿。

通过建模以软件方式补偿热误差是提升数控机床精度的重要方法［8-9］。该方法在分析机床热行为的机理上，研究热误差这一输出量和以温度测点温升为主的输入量之间的数学关系，以软件的方式补偿机床热误差，无需改变现有机床的硬件，兼顾了减小热误差影响的功能性和低成本使用的经济性，而且很容易应用在现有机床上。建立预测精度高、稳健性强的机床热误差补偿模型是以软件方式补偿热误差的最终目的。稳健性是指在复杂工况下维持准确结果的特性［1］。以软件方式建立稳健性热误差补偿模型需要解决两个重点问题：（1）选择合适的温度敏感点；（2）选择合适的建模算法。

合适的温度敏感点选择是建立稳健性热误差补偿模型的关键［9-10］。要建立预测精高、稳健性强的机床热误差补偿模型，参与建模的温度敏感点必须能最大限度地反映温度场的分布特性，同时还要降低彼此之间共线性的干扰［11-12］。在选出合适的温度敏感点的基础之上，再对建模算法进行选择。最小化残差是选择建模算法的核心思想，目标是模型带入建模数据的拟合误差最小。根据此思想，多元回归、岭回归、神经网络和支持向量机等均为常用的热误差建模算法［12-18］。

针对温度敏感点选择，目前高斯积分、灰色系统理论、模糊聚类方法和有限元仿真技术等被广泛运用于温度敏感点的选择［12-21］。这些方法多以分类选优思想为指导进行温度敏感点的选择，目的是减小温度敏感点之间的共线性，提升建模算法的稳健性。其中，模糊聚类和灰色关联在敏感点分类和优化中具有优势，该方法被广泛研究［14，18，22-23］。以模糊聚类结合灰色关联度选取温度敏感点策略［14］为例，该策略选出的温度敏感点能有效降低温度敏感点之间的共线性［9］，大幅提升机床热误差补偿模型的稳健性，但也存在温度敏感点变动的问题，而温度敏感点的变动会造成补偿模型精度的损失［10，12］。本文针对这一问题，从造成温度敏感点变动性的机理出发，解释了温度敏感点变动的产生原因，并在此基础上提出了一种稳健的温度敏感点选择方法，最后通过全年12 批次的实验数据验证了这一方法的有效性。分别使用稳健性温度敏感点选择方法和非稳健性选择方法建立了两个热误差补偿模型，分析发现，因未考虑温度敏感点变动而建立的模型，其拟合精度、预测精度及长期预测稳健性会大幅降低。基于机床稳健性温度敏感点选择方法的热误差补偿模型不仅可以避免模型精度的稳健性难以满足工况需求，而且可以实现用5 个温度传感器就将模型全年的预测精度均值控制为5.18 μm，全年的预测精度的波动性可以控制为2.57 μm。基于机床稳健性温度敏感点选择方法建立的模型具有优秀的预测精度和长期预测稳健性；机床稳健性温度敏感点选择方法提升了传统的“模糊聚类结合灰色关联度”方法的适用范围，具有重大的理论价值和工程应用价值。

2 实 验

机床是一个复杂的整体区域，热对机床的整体影响在加工过程中耦合表现为机床主轴相对于被加工工件的空间偏移。对于三轴C 型立式数控机床（以下简称机床）来说，由于机床整体结构设计关于YZ平面对称，主轴X向受热较均匀，热误差最小，Y向次之，Z向热误差最大。如图1所示，主轴Z向热误差可达X向热误差的8 倍左右、可达Y向热误差的2 倍左右，在不同批次实验中所表现的热变形量不同，但是热变形趋势类似。因此，本文针对变化最大机床主轴Z向热误差，通过全年的跟踪实验，提出的方法同样适用于对主轴Y向和X向热误差的补偿。

在不同转速、室内无空调的条件下共做了12 批次实验，热误差的测量采用国际标准《机床检验通则第3 部分：热效应的确定》（ISO 230-3：2001 IDT）［24］提出的五点测量法。依据本团队十余年的连续性研究和国际上其他学者的相关研究［13-14，25-26］，在机床关键部位布置了10 个温度传感器，热误差和温度数据采用同步采集的方式。

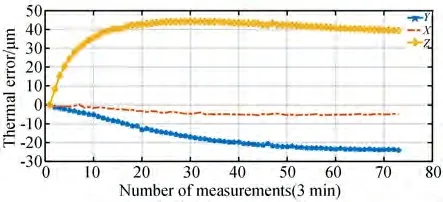
图1 三轴C 型立式数控机床的热误差Fig.1 Thermal errors of three-axis C-type vertical CNC machine tool

2.1 热误差测量装置

热误差测量装置参照国际标准《机床检验通则第3 部分：热效应的确定》（ISO 230-3：2001 IDT）［24］提出的五点测量法原理进行设计。由于文章针对机床主轴Z向热误差进行研究，故未使用测量X和Y向的位移传感器。测量装置如图2所示。

图2 中，检验棒材质为金属，固定于机床的主轴上；夹具材质与检验棒相同，固定在工作台上；电涡流微位移传感器的探头型号为CWY-DOTR-810803-00-04-50-01，前置器型号为CWYDO-TR-810800-50-01-02-04，测量分辨力可达亚微米，精度为±1 μm，它固定在夹具工具上。位移传感器用于测量检验棒在Z方向的位移，以测量热误差。

图2 热误差测量装置图Fig. 2 Diagram of thermal error measuring devices

2.2 温度传感器安放位置

在影响机床主轴Z向热误差的关键部位一共布置了10 个温度传感器，记为T1～T10，目的是对影响机床主轴Z向热变形的机床主要热源附近的温度进行测量。 温度传感器型号为DS18B20 型数字温度传感器，测温范围在-55～125 ℃，对温度的分辨率为0.062 5 ℃，测温精度可达±0.5 ℃（-10～85 ℃），采用磁吸附方式安放在机床上。温度传感器在机床上的安放位置示意图和实物图如图3～图4 所示，具体安装位置如表1 所示。表1 中，T1～T5温度传感器的具体安放位置在图4 中用箭头标出。

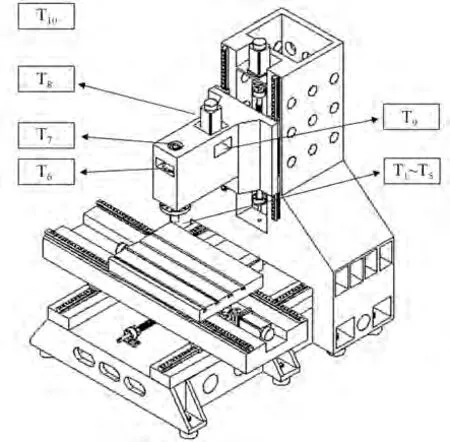
图3 温度传感器安放位置示意图Fig.3 Schematic diagram of temperature sensor installation positions

图4 温度传感器安放位置实物图Fig.4 Photo of temperature sensor installation positions

表1 温度传感器安放位置Tab.1 Installation positions of temperature sensors

2.3 热误差的测量过程

热误差的测量步骤如下：

步骤1：将位移传感器安装在夹具上，夹具装夹于主轴正下方，主轴下压至设定位置触发测量信号，同时测量并记录机床主轴Z向热误差初值和温度值。后续测量得到的热误差值为减去热误差初值的变动值。

步骤2：主轴上移，工作台不动，主轴以指定参数空转3 min。

步骤3：主轴停转，下压至设定位置触发测量信号，同时测量并记录主轴Z向热误差值和温度值。

步骤4：重复步骤2 和步骤3 直至机床达到热稳态，结束测定。

2.4 实验数据

以Leaderway-V450 数控加工中心的主轴Z向热误差为研究对象。实验采用工作台不动，主轴空转的方式，每3 min 测量一次实验数据，每次实验基本持续4 h 以上，得到了全年实验数据共12 批次。12 批次数据的实验条件按环境温度升序排列，具体参数如表2 所示。将12 批次数据中机床主轴Z向热变形绘制如图5 所示。

表2 12 批次实验数据的实验条件Tab.2 Experimental conditions of 12 batches of experimental data

3 温度敏感点变动性机理分析

采用较为成熟的“模糊聚类结合灰色关联度”进行温度敏感点的选择，并针对其变动机理进行分析。

3.1 模糊聚类

模糊聚类就是用模糊数学的理论去研究聚类问题，在机床热误差建模技术中，模糊聚类算法用于将相似的温度测点聚为一类，为进一步利用灰色关联度筛选参与建模的温度敏感点做准备。其具体步骤为：

（1）建立模糊相似矩阵：将温度测点之间的相似程度转换为0～1 之间的模糊关系。

设xi(i=1，2，…，m)为数控机床m个温度变量数据，xi(k)(k=1，2，…，n)为第i个温度变量的第k个测量值。通过计算相关系数rij(1≤i，j≤m)来确定模糊相似矩阵R=(rij)m×m。

（2）建立模糊等价矩阵：使得温度测点之间的模糊关系具有传递性，否则无法进行聚类。

重新定义乘法和加法运算，认为：A×B=min(A，B)；A+B=max(A，B)。

在此基础上采用平方法经过有限次运算求出R的传递闭包（包含R的最小传递模糊关系的矩阵称为R的传递闭包），R^ 就是一个模糊等价矩阵。

（3）判定系数分类：将模糊关系大于某一阈值的温度测点归为一类，阈值称为判定系数。

3.2 灰色关联度分析

灰色关联度分析是量化被分析数据序列之间的联系紧密程度的一种方法。灰色关联度计算值越大，则相应序列之间的关联度就越大，反之越小。

图5 12 批次数据中机床主轴Z 向热变形Fig.5 Thermal deformation data of 12 batches of machine tool spindle in Z-direction

本文采用邓氏灰色关联度分析方法，计算公式为［9］：

其中：y代表热误差；xi代表为第i个温度测点观测值，i=1…m，m为温度测点个数；y(k)，xi(k)分别代表热误差的第k个观测值和第i个温度测点的第k个观测值；γ(y，xi)为热误差和第i个温度测点之间的灰色关联度；ρ为分辨系数，在[0，1] 之间取值，一般取ρ=0.5；Δy(k)，xi(k)=|y(k)-xi(k)|，为热误差序列与温度传感器测得数据序列的绝对差值，形成的绝对差值矩阵为(Δy(k)，x1(k)…Δy(k)，xi(k)…Δy(k)，xm(k))；Δmin和Δmax为这个矩阵中的最小数和最大数。

3.3 温度敏感点选择

采用模糊聚类结合灰色关联度方法从12 批次数据中选取出的温度敏感点如表3 所示。

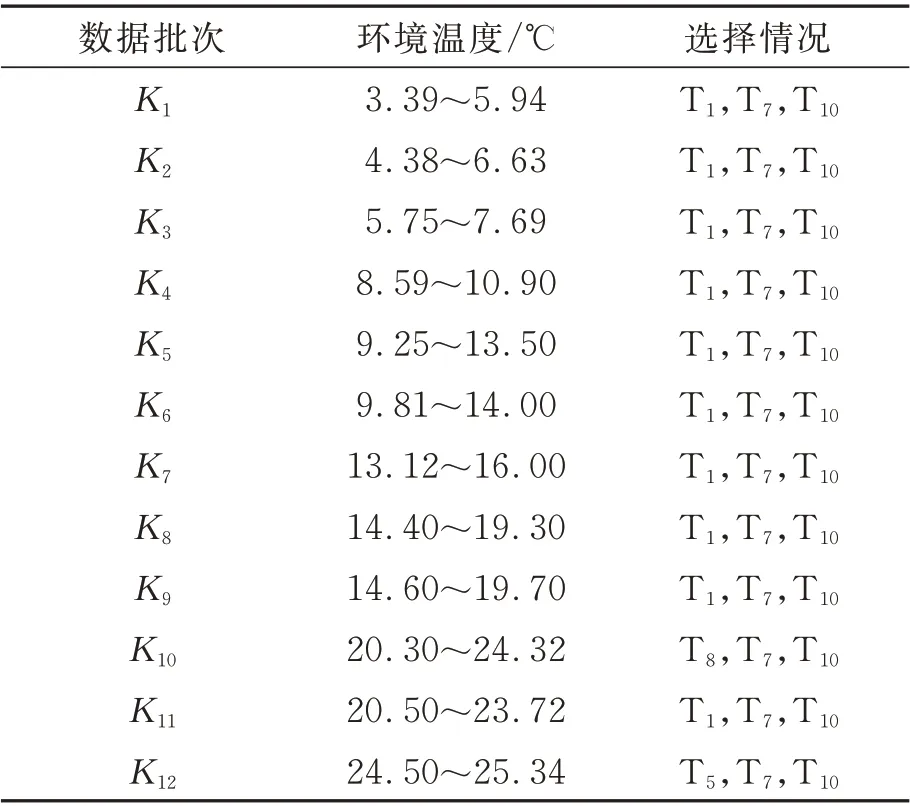
表3 温度敏感点选择情况Tab.3 Selection results of temperature-sensitive points for 12 batches of data

由表3 可知，12 批次数据选出的温度敏感点大部分为T1，T7，T10，这3 个测点位置发热量较大且在各类中与机床热变形关联权重最大，但也出现了选择T8，T5的情况。显然，采用模糊聚类结合灰色关联度方法选择出的温度敏感点具有变动性。当某个温度测点受到干扰时，可能会造成误选温度敏感点的现象。为解决选择的温度敏感点变动性缺陷，需要对其机理进行研究分析。

3.4 温度敏感点变动性机理

模糊聚类结合灰色关联度选择温度敏感点的指导思想是分类选优。分类后温度测点与热误差的灰色关联度的变动是造成温度敏感点变动的主要原因。灰色关联度公式为：

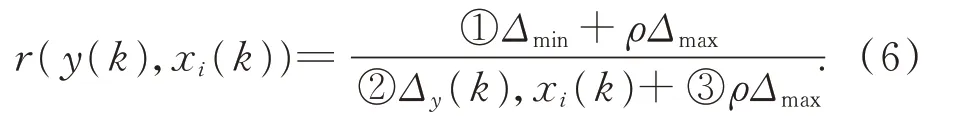
将公式分为3 个部分当温度敏感点选定后，第①部分和第③部分皆为定值。第②部分的实质为热误差和第i个温度测点在第k个观测值的差的绝对值，第2 部分的值越小，r(y(k)，xi(k))的值越大，表明温度测点和热误差变化曲线越接近，即灰色关联通过变量变化曲线的几何相似程度来判断温度测点和热误差之间的相关性。这会造成某个温度测点或者热误差的测量意外受到扰动，如：温度传感器、位移传感器电平短时失稳等。干扰造成的温升曲线波动或热误差测量曲线波动会使得该测点与热误差之间的灰色关联度的值下降。

如图6 所示，（a）图中1 号温度传感器测得的温升曲线与热误差测量曲线的相关性比（c）图中2 号温度传感器测得的温升曲线与热误差测量曲线的相关性更高，但由于意外的测量扰动使得（a）图中1 号温度传感器的温升曲线产生波动，变成了（b）图中所示的1 号温度传感器温升曲线，由此导致1 号温度传感器温升曲线与热误差变化曲线的几何相似程度降低，就会造成使用灰色关联度选取温度敏感点时，会错误地选出（c）图中的2号温度测点作为温度敏感点。

由温度敏感点变动性的机理分析可知，在模糊聚类过后的类中选优过程中，使用灰色关联度算法选取温度敏感点不具备足够的稳健性。当温度传感器或热误差测量传感器受到偶然的扰动致使温升曲线或热误差测量曲线产生波动时，由于是通过变量变化曲线的几何相似程度来判断温度测点和热误差之间的相关性，灰色关联度有时不能选取出每类中与热误差相关性最大的温度测点。

图6 灰色关联度原理造成温度敏感点选择波动示意图Fig.6 Schematic diagram of temperature sensitive point selection fluctuation caused by grey correlation degree principle

本文针对造成变动性缺陷的机理，对温度敏感点选择情况进行了进一步的分析，提出了稳健性温度敏感点选择方法。该方法解决了灰色关联度误判温度测点的缺陷，提升了温度敏感点选择的科学性和稳健性。

4 稳健性温度敏感点选择及热误差模型建立

4.1 稳健性温度敏感点选择方法

12 批次温度传感器数据通过模糊聚类得到的聚类结果如表4 所示。由于聚类结果中第二类皆为T7，第三类皆为T10，限于篇幅，将之省略，仅展示第一类的分类情况。第一类中的测点位置顺序按由式（6）计算出来的灰色关联度降序排列。

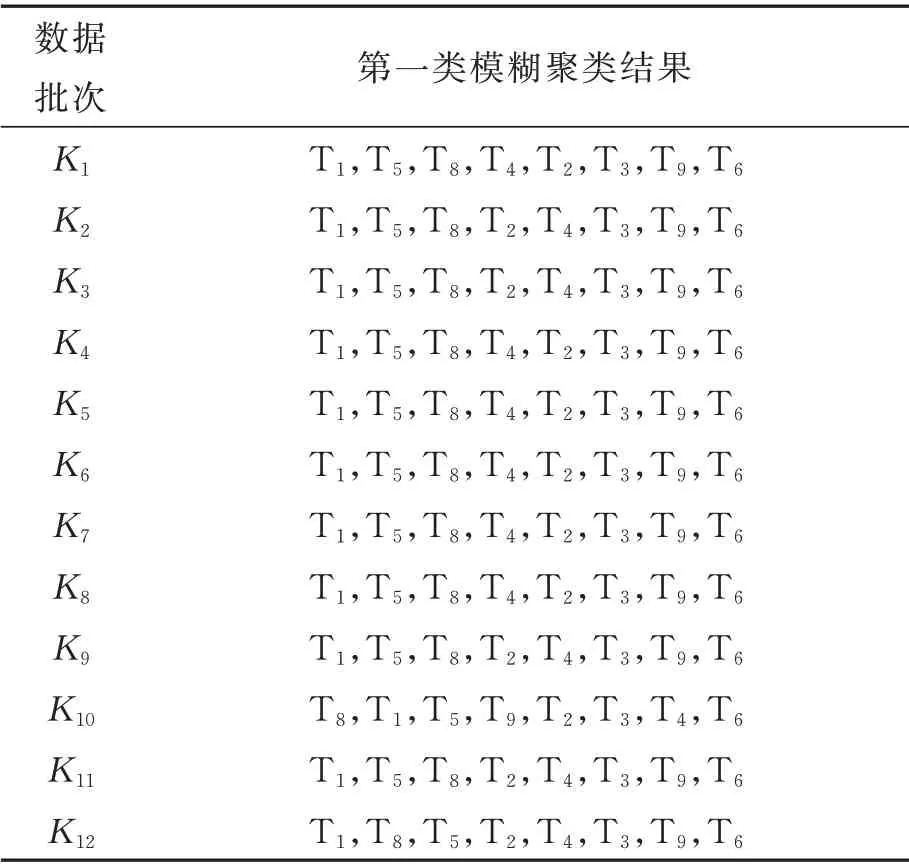
表4 12 批次温度传感器数据模糊聚类结果（第一类）Tab.4 Fuzzy clustering results of 12 batches of temperature sensor data（First class）

从表4 中可以看出，虽然第一类中各温度测点的灰色关联度排序出现了变动性，但是排名前3 的测点始终是T1，T5和T8。针对造成变动性缺陷的机理，基于增强温度测点选择稳健性和减小温度测点之间共线性影响的思想，提出扩大温度敏感点选择范围的稳健性温度敏感点选择方法，以提高代入模型的温度敏感点选择稳健性，即选择第一类中灰色关联度排名前三的测点和第二类、第三类中排名第一的测点作为温度敏感点。

虽然消除误差的手段有很多，但重要的是了解误差产生的原因，并有针对性地进行解决。稳健性温度敏感点选择方法很明显已经消除了“模糊聚类结合灰色关联度”方法中由于灰色关联度原理缺陷造成的温度敏感点选择变动性。为验证稳健性温度敏感点选择方法选择出的温度敏感点的正确性，这里采用多元线性回归算法分别以T1，T5，T8，T7，T10和T8，T7，T10的数据为自变量建立机床热误差补偿预测模型。

4.2 热误差模型及精度分析

4.2.1 两种模型的建立

将稳健性温度敏感点选择方法选择的温度敏感点T1，T5，T8，T7，T10带入多元线性回归算法进行建模，结合全年12 批次数据建立了模型RM1～R-M12。由于篇幅关系，仅列举部分模型如下：

R-M1～R-M12 相互预测的预残差标准差如图7 所示，其中拟合看成模型对自身的预测。

预测残差标准差用于表示预测精度，其计算公式为：

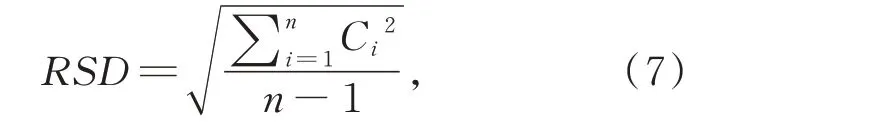
式中：Ci为预测模型对第i个热变形测量数据的预测残差，n为一批次数据量大小。

图7 R-M1～R-M12 相互预测的预测残差标准差Fig.7 Prediction residual standard deviation of R-M1-R-M12 mutual prediction

从图7 可以看出，基于T1，T5，T8，T7，T10代入多元线性回归算法建立的模型的预测精度良好；在对第10 批次和第12 批次数据进行预测时，由于第10 批次和第12 批次数据遭受了干扰，预测精度出现了一定幅度的波动。总体上看，模型的预测精度基本保持在10 μm 以内。

将未采用稳健性温度敏感点选择方法而误选出的温度敏感点T8，T7，T10带入多元线性回归算法进行建模，结合全年12 批次数据建立了模型E-M1～E-M12。由于篇幅关系，仅列举部分模型如下：

E-M1：y=2.20+5.25x1-0.09x2+0.47x3，

E-M12：y=2.30+5.78x1+0.17x2-0.21x3.

E-M1～E-M12 相互预测的预测残差标准差如图8 所示，其中拟合看成模型对自身的预测。

从图8 中可以看出，由于T8不是稳健的与热误差相关性最大的温度敏感点，扰动较大。T8，T7，T10代入多元线性回归算法建立的模型与稳健性温度敏感点选择方法选择的T1，T5，T8，T7，T10代入多元线性回归算法建立的模型相比，预测精度和预测精度的稳健性均大幅下降。

4.2.2 两种模型的精度分析

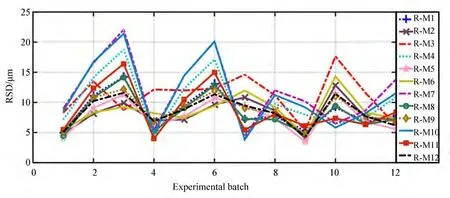
图8 E-M1～E-M12 相互预测的预测残差标准差Fig.8 Prediction residual standard deviation of E-M1～E-M12 mutual prediction

对全年12 批次实验数据采用稳健性温度敏感点选择方法选择的温度敏感点T1，T5，T8，T7，T10带入多元线性回归算法所建立模型和未采用稳健性温度敏感点选择方法选出的温度敏感点T8，T7，T10带入多元线性回归算法所建立模型进行精度分析，结果如图9～图10 所示。其中，S为模型的拟合标准差，用来表征模型的拟合精度，其值越小，说明模型的拟合精度越高；Sm为模型对其他批次数据的预测残差标准差均值，用来表征模型的预测精度，其值越小，说明模型的预测精度越高；Sd为模型对其他批次数据预测残差标准差的标准差，用来表征模型预测精度的离散程度，其值越小，说明模型的稳健性越高。

Sm和Sd的计算公式为如下：

式中：Sri为模型对其他批次数据的预测残差标准差；n=11，为预测数据批次数。

图9 R-M1～R-M12 精度分析Fig.9 Accuracy analysis of R-M1-R-M12 models

从图9 和图10 中可以看出，使用稳健性温度敏感点选择方法建立的模型对于全年12 批次数据的拟合精度均值（2.85 μm）、预测精度均值（5.18 μm）和长期预测稳健性均值（2.57 μm），对比未使用稳健性温度敏感点选择方法建立的模型的拟合精度均值（6.48 μm）、预测精度均值（9.55 μm）和长期预测稳健性均值（3.55 μm），稳健性分别提升了56.0%，45.8% 和27.6%。温度敏感点选择的波动性对于数控机床热误差模型的精度影响很大。由于温度敏感点波动而代入错误的温度敏感点建立模型，会造成模型拟合精度、预测精度和长期预测稳健性的大幅损失。基于机床稳健性温度敏感点选择方法的热误差补偿模型不仅可以避免模型稳健性难以满足工况需求，而且可以避免带入错误温度敏感点建模，用5 个温度传感器就将模型全年的预测精度均值控制在5.18 μm，预测精度波动控制在2.57 μm，模型具有优秀的预测精度和长期预测稳健性。

图10 E-M1～E-M12 精度分析Fig.10 Accuracy analysis of E-M1～E-M12 models

5 结 论

建立预测精度高、稳健性强的机床热误差补偿模型是研究机床热误差模型的最终目的，本文通过对较为成熟的模糊聚类结合灰色关联度方法进行深入研究，在充分分析温度敏感点变动性机理的基础上提出稳健性温度敏感点选择方法，提升了传统方法的适用范围，运用该方法在全年时间内实现了良好的补偿效果，为研究如何选择稳健的温度敏感点来建立机床热误差补偿模型开拓了新的思路。

温度敏感点选择的波动性对于数控机床热误差模型的精度影响很大。本文根据造成变动性缺陷的机理，提出扩大温度敏感点的选择范围以提高代入模型的温度敏感点选择稳健性的温度敏感点选择方法。并通过全年12 批次实验数据验证了这一方法消除温度敏感点选择变动的有效性和所选出温度敏感点的正确性。基于机床稳健性温度敏感点选择方法建立的热误差补偿模型，在数控机床上根据全年实验验证应用，结果显示：使用机床稳健性温度敏感点选择方法建立的热误差补偿模型不仅可以避免模型精度的稳健性难以满足工况需求，而且可以避免带入错误温度敏感点建模，用5 个温度传感器将模型全年的预测精度均值控制在5.18 μm，全年的预测精度的波动控制在2.57 μm。该模型具有优秀的预测精度和长期预测稳健性，机床稳健性温度敏感点选择方法具有重大的理论价值和工程应用价值。