考虑关断时间的地面瞬变电磁三维带地形反演
齐彦福, 智庆全,3, 李貅*, 景旭, 戚志鹏,孙乃泉, 周建美, 刘文韬
1 长安大学地质工程与测绘学院, 西安 7100542 长安大学地球物理场多参数综合模拟实验室, 西安 7100543 中国地质科学院地球物理地球化学勘查研究所, 河北 廊坊 065000
0 引言
随着经济的快速发展,我国对矿产资源的需求不断增加,然而经过数十年的不间断开采,地形相对平坦、地质条件简单的浅部矿藏已经开采殆尽,找矿工作正在向地形起伏严重的山区进军.地面瞬变电磁法作为一种低成本、高效率的地球物理勘探方法,已经在矿产资源勘查领域获得广泛应用(薛国强等,2007;底青云等,2019).然而,在过去的数十年中受到计算机条件和数据解释技术的制约,地面瞬变电磁数据解释工作主要以视电阻率成像和一维反演方法为主(薛国强等,2008;石显新等,2009;武军杰等,2013),此类方法在地形平坦、地下介质成层性明显的地区可以获得很好的应用效果,然而在地形起伏严重、三维地电结构发育的山区,利用一维处理解释技术很难获取准确的地下三维电性分布信息.开发适用于起伏地形的瞬变电磁三维反演算法,已成为瞬变电磁数据精细化解释的关键.
作为反演的基础,前人在瞬变电磁三维正演算法方面开展了大量工作,开发了一系列三维正演方法(汤井田等,2007),例如频时转换法(殷长春等,2013)、时间域有限差分法(Wang and Hohmann,1993;Commer and Newman,2004)、时间域有限体积法(Haber et al.,2007;Oldenburg et al.,2013)和时间域有限元法(Yin et al.,2016;Cai et al.,2017).频时转换法首先计算三维频率域电磁响应,然后采用频时转换技术将其转换到时间域,完成瞬变电磁响应模拟.时间域有限差分法是一种基于交错网格和显式时间差分格式的直接时间域正演算法(孙怀凤等,2013),该方法数学概念直观,表达简单,但是需要满足Courant稳定性条件,使得网格尺寸和时间步长均受到严格限制.近年来,随着计算机性能的大幅提升和大型方程组求解技术的快速发展,基于隐式时间差分格式的三维正演算法取得了重大技术突破,其优势逐渐展现出来.时间域有限体积法(Yang et al.,2014)和时间域有限元法(齐彦福等,2017)通过采用后退欧拉时间离散格式对控制方程进行无条件稳定的隐式时间离散,极大地放宽了对时间步长的限制.与有限体积法所采用的规则六面体网格不同,时间域有限元法可以采用非规则四面体网格进行空间离散.基于四面体网格的灵活性,该方法在处理起伏地形和复杂地电结构时显示出明显优势.Li等(2018)采用时间域有限元方法模拟了复杂形状发射源地面瞬变电磁响应,结果表明地形起伏和发射线圈形状的变化对观测响应影响极大,其导致观测响应发生复杂畸变.Zeng等(2019)进一步分析了关断时间对瞬变电磁响应的严重影响.
在三维反演方面,目前三维电磁反演算法主要有高斯牛顿法、非线性共轭梯度法和拟牛顿法.高斯牛顿法通过近似计算Hessian矩阵和目标函数的梯度获得模型改变量,然后采用线性搜索方式获得最佳的模型更新步长,实现模型迭代更新.该算法具有超线性收敛特性(Haber et al.,2007),但是需要计算灵敏度矩阵的乘积来近似Hessian矩阵,导致每次迭代过程的计算量巨大.非线性共轭梯度法首先计算目标函数在当前参考模型下的负梯度,并在梯度的共轭方向搜索最优步长使得目标函数达到极小值,进而实现反演模型更新(翁爱华等,2012).由于该方法在每次反演迭代过程中无需计算灵敏度矩阵,因此计算量明显减少,然而该算法为线性收敛,反演收敛速度较慢(Newman and Commer,2005).L-BFGS法是一种有限内存的拟牛顿反演算法,该算法通过伴随正演计算目标函数的梯度,再采用迭代方式近似计算Hessian矩阵的逆,因此每次反演迭代只需要一次正演和一次伴随正演即可完成模型更新.与非线性共轭梯度法相比,L-BFGS算法在计算时间和模型反演分辨率上更具优势(刘云鹤和殷长春,2013).Liu等(2019)基于非结构时间域有限元法和L-BFGS算法实现了瞬变电磁三维带地形反演.
三维反演技术的发展在提高瞬变电磁数据解释精度的同时,也为改进观测模式、提高工作效率提供了技术支撑.在传统的定源回线装置野外工作中,由于受到中心回线近似解释方法的限制,数据采集只能在发射线圈中心三分之一区域进行,但是三维反演技术的出现彻底打破了这种限制,可以在发射线圈内外任意位置进行三维观测,使得瞬变电磁的观测方式变得更加灵活,同时这种三维观测方式极大地提高了野外施工效率.然而,观测模式的改进也带了一些新的问题.考虑到信号强度随收发距离的几何衰减规律,要实现基于三维观测模式的大深度探测必须加大发射功率.受到当前电子元器件条件的限制,当发射大电流时,无法实现瞬间断电,需要较长关断时间,此时不能够再采用理论阶跃波形近似.由于关断时间对瞬变电磁响应具有严重影响(孙怀凤等,2013;杨海燕等,2019;Zeng等,2019),因此在瞬变电磁三维反演过程中必须考虑关断时间.为此本文开展考虑关断时间的地面瞬变电磁三维带地形反演算法研究,以提高瞬变电磁数据解释的精细化程度.我们首先介绍本文所采用的非结构时间域有限元正演理论和瞬变电磁三维反演算法,然后将本文算法应用于理论和实测数据三维反演中以检验本文算法的有效性,并分析地形和关断时间对三维反演效果的影响特征.
1 非结构时间域有限元正演理论
从时间域麦克斯韦方程组出发,并忽略位移电流项,建立电场扩散方程
其中r是空间位置矢量,t是时间,e(r,t)是r处t时刻的电场,js(r,t)是源电流密度,μ和σ分别是磁导率和电导率.采用基于非结构四面体网格的矢量有限元方法对电场扩散方程进行空间离散,则任意四面体单元内的电场均可表示为(齐彦福等,2017)
(2)

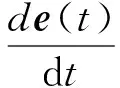
(3)
其中M和S分别为质量和刚度矩阵,Js是电流源项.
采用二阶后退欧拉离散格式对(3)式进行时间离散,得到无条件稳定的隐式差分方程:
(3M+2ΔtS)em+2(t)=M(4em+1(t)-em(t))
(4)
其中em(t)表示第m时刻的电场,Δt为时间步长.
在瞬变电磁法工作过程中,需要在地表敷设一个很大的发射线圈,当遇到地形起伏时,发射线圈也会随着地形起伏,使得发射线圈的形状和有效面积发生变化,为了模拟发射线圈的实际形状和尺寸,本文采用基于偶极子离散的场源处理方法(Yin et al.,2016)精细模拟实际场源.通过将发射线圈离散成若干段收尾相连的短导线,每段导线当作一个电偶极子进行处理,并考虑发射线圈与四面体单元任意空间相交关系,实现复杂发射场源的模拟.为了模拟断电时间的影响,本文采用瞬时电流脉冲技术(齐彦福等,2017),通过在每个时刻的右端源项中加载瞬时电流脉冲强度,实现考虑关断时间的瞬变电磁响应三维正演.
关于边界条件,本文采用均匀半空间狄利克雷边界条件(Yin et al.,2016),假设计算区域外边界的切向电场分量为0,即
(5)
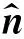
关于初始条件,由于在供电前,没有发射信号,因此空间任意处的电场均为0,即
e(r,0)=0.
(6)
然后,采用多波前并行求解器MUMPS(Amestoy et al.,2006)对(4)式进行求解即可获得各个时刻空间电场分布,再利用法拉第电磁感应定律计算接收点处的观测场值.
2 瞬变电磁三维反演算法
2.1 目标函数建立及正则化方法
首先建立目标函数
(7)
其中m是M维地电模型参数向量,dobs是N维观测数据向量,本文中dobs所包含的元素是各个测点不同时间道的dBz/dt响应,Wd和Wm分别是数据和模型方差矩阵,d是当前模型的正演数据,mref是先验参考模型,λ是正则化因子.(7)式中第二项是正则化项,其主要作用是压缩反演模型空间,改善反演的稳定性.利用模型方差矩阵Wm可以约束当前单元与相邻单元间模型参数的空间变化率,从而获得光滑的反演模型.本文根据Key(2016)提出的二维非结构网格空间约束矩阵建立方法,综合考虑与当前单元相邻的所有单元的电性相关性,并将其推广到三维情况(Liu et al.,2019),建立如下Wm矩阵
(8)
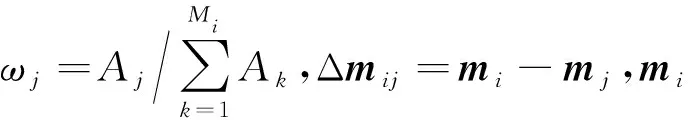

图1 模型空间约束Fig.1 Spatial constraint for inversion model
λ的选取至关重要,将直接影响反演的收敛速度和反演效果,本文采用“金属冷却法”(Haber,2014)选取每次反演迭代的λ,即首先人为设定一个较大的初值加强模型约束强度来保证反演的稳定性,然后利用当前λ进行反演迭代,当数据拟合差下降非常缓慢或不下降时减小λ,降低模型约束强度,通过不断重复上述过程实现数据拟合.
2.2 L-BFGS反演算法
本文采用Nocedal(1980)提出的有限内存拟牛顿法(L-BFGS)实现瞬变电磁数据三维反演.拟牛顿算法(BFGS)的核心是近似计算海森矩阵的逆H,为此首先给定一个对称正定矩阵H0作为初始海森矩阵的逆,本文中H0取为单位对角矩阵,然后利用
(9)
mn+1=mn+αnqn.
(10)
本文采用线性搜索的方式获得αn,首先给定初始αn=1,然后逐步减小αn,使其满足Wolf条件(Nocedal and Wright, 2006)
(11)
其中0<β<0.5,β<γ<1,F为正演算子.
2.3 目标函数梯度的计算
根据(9)式可知,在L-BFGS算法中近似计算海森矩阵逆的基础是获得目标函数的梯度,本文基于伴随正演算法计算目标函数的梯度.首先通过对目标函数求导可以获得目标函数梯度的表达式
(12)
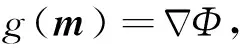
(13)
由于(13)式中等号右端第二项很容易计算,因此计算目标函数梯度的核心是计算JTr.我们首先将所有时刻的正演问题简写为
Ae=b,
(14)
则有
e=A-1b.
(15)
由于瞬变电磁法观测的是dB/dt响应,由(15)式可以得到
(16)
其中Q是插值矩阵.灵敏度矩阵可写成
(17)
则有
JTr=GTA-TQTr,
(18)

JTr=GTv,
(19)
其中v=A-TQTr.v通过求解伴随正演方程
ATv=R,
(20)
进行计算.通过逆向时间迭代获得向量v之后即可代入(19)式计算JTr,进而获得目标函数的梯度,完成模型更新.
3 理论模型反演
3.1 地形对三维反演结果的影响特征
为了检验本文算法的有效性,我们首先设计了如图2所示三维起伏地表模型,地形最大起伏高差约为150 m,背景围岩电阻率为100 Ωm,在观测区域的中心位置埋藏一个电阻率为10 Ωm的良导梯形体,梯形体顶面边长为200 m,底面边长为400 m,梯形体的高为100 m,顶面埋深约为200 m.观测系统采用定源回线装置,发射线框边长为650 m,发射电流为10 A的阶跃波,基于传统观测模式在发射线框内部进行测量,为了完成整个区域的观测,共布置了9个发射线圈,每个线框内均匀分布8×8=64个测点,共576个测点,点距和线距均为50 m,每个测点观测从10 μs到10 ms的31道对数等间隔dBz/dt响应数据.我们在理论数据中加入5%的随机噪声作为观测数据,然后利用本文开发的三维反演算法进行反演.本文中的所有反演算例均在PC机上进行,CPU主频3.20 GHz,共6个计算核心,内存64 GB.
为了研究地形对三维反演结果的影响,本文分别采用起伏地形和水平地表两种模型完成反演,初始模型和参考模型均采用100 Ωm的半空间模型,初始正则化因子λ均设定为10,然后采用“金属冷却法”获得每次反演迭代的λ.反演网格的核心区域范围如图3所示,然后在x、y、z三个方向分别设定100000 m的扩边区域,使其满足狄利克雷边界条件.起伏地形反演网格包含478958个四面体单元,而水平地表反演网格包含435644个四面体单元.图3展示了经过13次迭代的反演结果.从图中可以看出带地形反演结果(图3a—c)与真实模型(图2)吻合较好,能够清晰反映出地下的电性分布情况,较为准确地显示了良导目标体的位置和尺寸.然而水平地表模型的反演结果(图3d—f)虽然也可以获得地下目标的大体分布情况,然而为了强制拟合地形数据,在反演结果中出现了大量假异常,而且这些虚假异常不仅局限于地表,在深部同样存在,虚假异常的出现将给后续的地质解释造成很多困难.该反演结果有效验证了本文算法的可靠性,同时也说明了起伏地形对三维反演结果会产生巨大影响.图4和图5展示了两组反演结果的数据拟合情况.可以看出,考虑地形的三维瞬变电磁反演可以很好地拟合观测数据,而且反演收敛速度很快,反演共耗时37.39 h,所占内存为22.5 GB.然而,在不考虑地形情况下,通过产生一些局部的虚假异常同样可以达到数据拟合的目的,但是在数据拟合到一定程度后无法找到合理的三维模型实现进一步的数据拟合,而且由于不合理反演模型的试探次数较多,反演共耗时128.36 h,所占内存为20.8 GB.
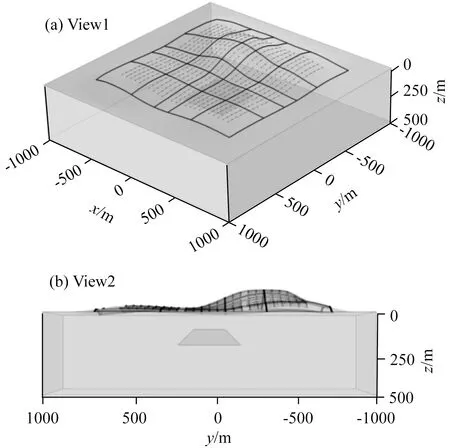
图2 起伏地表梯形良导体模型(a)和(b)分别是不同角度的三维透视图.Fig.2 Topographic model with a trapezoidal conductor(a) and (b) are perspective views from different directions.

图3 考虑和忽略地形影响的反演结果对比图(a)—(c) 起伏地表模型反演结果; (d)—(f) 水平地表模型反演结果.Fig.3 Comparison of inversion results with and without topography(a)—(c) are inversion results for a topographic earth; (d)—(f) are for a flat earth.

图4 数据拟合结果(a)—(c) 含噪声的理论数据; (d)—(f) 起伏地表反演模型的正演数据; (g)—(i) 水平地表反演模型的正演数据.Fig.4 Data fitting for invesion results(a)—(c) Synthetic data; (d)—(f) Predicted data from the inverted model with topography; (g)—(i) Predicted data from the inverted model without topography.
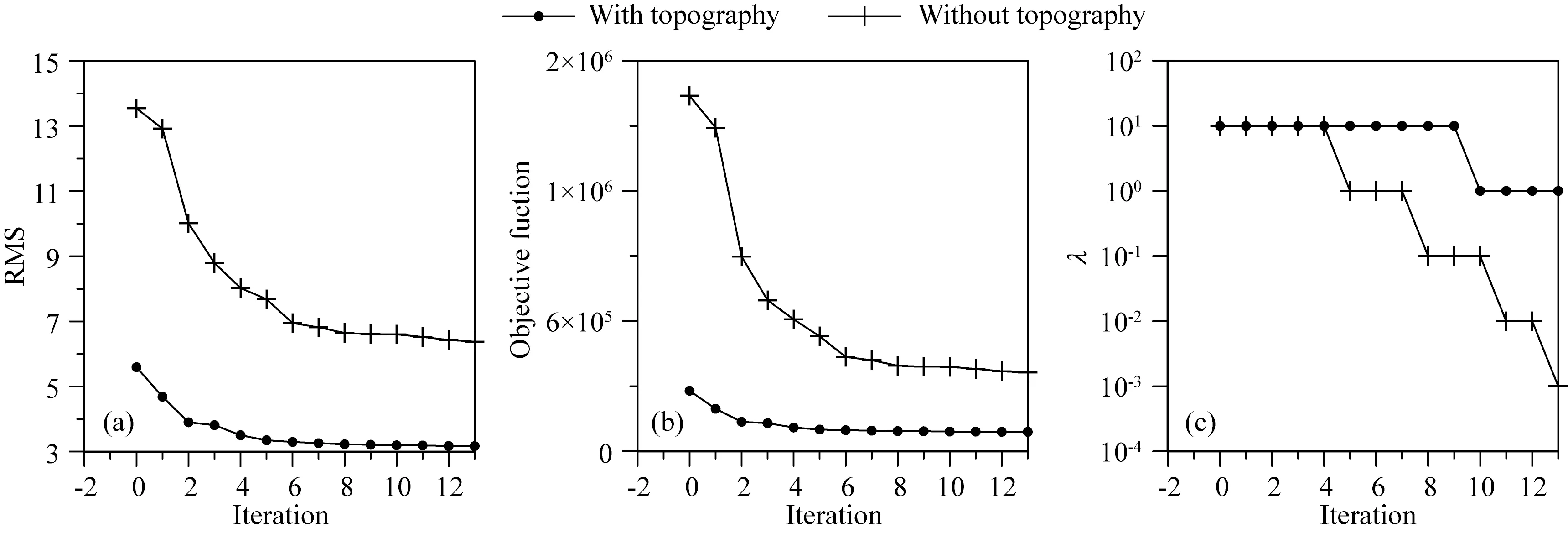
图5 考虑和忽略地形影响的反演迭代参数(a) 均方根误差; (b) 目标函数; (c) 正则化因子λ.Fig.5 Inversion parameters versus iterations for considering and ignoring topography(a) Root-mean-square error; (b) Objective function; (c) Parameter λ.
3.2 关断时间对三维反演结果的影响特征
本文设计了如图6所示的起伏地表模型,地形最大起伏高差约为380 m.在100 Ωm的半空间中埋藏一个电阻率为10 Ωm的良导L形目标体,目标体位于发射线圈正下方,沿x和y方向的长度均为700 m,宽度和高度均为200 m,顶面埋深约为300 m.观测装置采用定源回线装置,发射线圈边长为1000 m,发射如图7所示的电流波形,其中供电时间ton=19 ms,关断时间tramp=100 μs,峰值电流为20 A.在发射线圈内外同时进行观测,共观测16×16=256个测点,点距和线距均为100 m.每个测点观测从发射电流完全关断后10 μs到10 ms的31道对数等间隔dBz/dt响应数据.我们在理论数据中加入5%的随机噪声作为观测数据,然后利用本文开发的三维反演算法进行反演.
为了分析关断时间对三维反演结果的影响,我们采用考虑关断时间和理论阶跃波两种电流波形对观测数据进行反演.初始模型和参考模型均采用100 Ωm的半空间模型,初始正则化因子λ均为0.01,然后采用“金属冷却法”获得每次反演迭代的λ.反演网格的核心区域范围如图8所示,然后在x、y、z三个方向分别设定100000 m的扩边区域,使其满足狄利克雷边界条件.反演模型网格包含535752个四面体单元.图8展示了经过30次迭代后的两种电流波形的反演结果.从图中可以看出考虑关断时间的反演结果(图8a—c)与真实模型(图6)吻合较好,能够清晰反映出地下的电性分布情况.然而理论阶跃波形的反演结果(图8d—f)虽然也可以获得地下目标的大体分布,但是在反演结果中出现了很多假异常,且大部分集中在地表,这是由于关断时间的变化主要影响瞬变电磁响应断电后早期的电磁响应,这种影响随着时间的增加逐渐减弱.虚假异常的出现严重影响了瞬变电磁数据三维解释精度.图9和图10展示了两组反演结果的数据拟合情况.可以看出,考虑关断时间的三维瞬变电磁反演可以很好地拟合观测数据,而且反演收敛速度很快,反演共耗时12.56 h.然而,在不考虑关断时间的情况下数据拟合情况并不理想,尤其是早期数据无法拟合(如图9所示),导致错误的模型搜索方向,进而在一定程度上影响深部目标体的反演效果.由于不合理反演模型的试探次数较多,反演共耗时16.37 h.两种模型反演所占内存均为20.3 GB.

图7 发射电流波形Fig.7 Transmitting current

图8 考虑和忽略关断时间影响的反演结果对比图(a)—(c) 考虑关断时间的三维反演结果; (d)—(f) 理论阶跃波形的反演结果.Fig.8 Comparison of inversion results for considering and ignoring ramp time(a)—(c) Inversion results considering ramp time; (d)—(f) Inversion results ignoring ramp time.

图9 x=50 m测线数据拟合情况Fig.9 Data fitting for survey line x=50 m

图10 考虑和忽略关断时间影响的反演迭代参数(a) 均方根误差; (b) 目标函数; (c)正则化因子λ.Fig.10 Inversion parameters versus iterations for considering and ignoring ramp time(a) Root-mean-square error; (b) Objective function; (c) Parameter λ.
4 实测数据反演
我们将本文开发的三维反演算法应用于青海夏日哈木矿区的实测数据解释中.夏日哈木铜镍矿区地处柴达木盆地西南缘,是东昆仑成矿带新发现的一处超大型岩浆熔离型铜镍硫化物矿床,超基性岩体具有多期次侵入的特征,岩性较为复杂,整体上深部矿体品位相对上部较高.矿区出露地层为古元古代金水口岩群白沙河组,主要岩性有黑云斜长片麻岩、云母二长片麻岩、斜长角闪岩、大理岩等.区域内岩浆岩较为发育,主要形成于古特提斯造山旋回的不同阶段,主要由早二叠世闪长岩、晚三叠世花岗岩等组成(杜玮等,2014).围岩导电性较差,最高电阻率可达1000 Ωm以上.然而工业矿体的导电性良好,最低电阻率可达3.5 Ωm.研究区内地貌主要为戈壁荒漠及残山景观,近山脊基岩裸露、地形较陡峻,沟谷风尘黄土覆盖.为完成对地下矿体的勘探,在测试区内敷设一个600 m×600 m的发射线框,共布置5条测线,线距80 m,点距50 m,共83个测点(如图11所示),其中L2和L3测线与地质勘探线重合.发射如图7所示的电流波形,其中供电时间ton=20 ms,关断时间tramp=1 ms,峰值电流为15 A.每个测点观测从发射电流完全关断后54 μs到16 ms的31道对数等间隔dBz/dt响应数据.
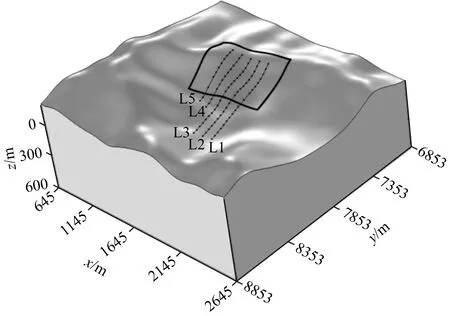
图11 发射源和测线空间分布Fig.11 Transmitting loop and survey lines over topographic survey area
为了更加准确地反映实际情况,我们在反演过程中同时考虑了起伏地形和关断时间的影响.初始模型和参考模型均采用200 Ωm的半空间模型,初始正则化因子λ设定为0.01,然后采用“金属冷却法”获得每次反演迭代的λ.反演网格的核心区域范围如图12所示,然后在x、y、z三个方向分别设定100000 m的扩边区域,使其满足狄利克雷边界条件.反演模型网格包含373072个四面体单元.经过38次迭代反演收敛.图12展示了考虑关断时间的三维带地形反演结果透视图,从图中可以看出,良导矿体沿x轴方向延伸,大体垂直于测线方向.图13显示三维反演展示的低阻区域与矿体的空间位置基本吻合,矿体埋深约为300 m,矿体主要分布在y=7853到y=8253之间,这一结果进一步验证了本文算法的有效性.从图14可以看出在反演初始阶段数据拟合差和目标函数下降较快,随着迭代的进行,下降速度逐渐减小,此时需要减小正则化因子λ,减弱对模型的约束强度,实现进一步的数据拟合.反演共耗时20.11 h,占用内存约为17.9 GB.

图12 三维反演结果透视图Fig.12 Perspective view of the 3D inversion model

图13 三维反演结果与地质勘探线剖面图Fig.13 3D inversion model and geological profile
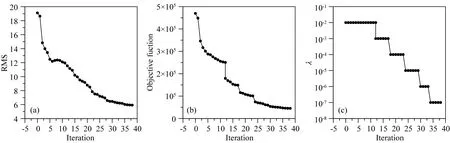
图14 反演迭代参数(a) 均方根误差; (b) 目标函数; (c) 正则化因子λ.Fig.14 Inversion parameters versus iterations(a) Root-mean-square error; (b) Objective function; (c) Parameter λ.
5 结论
本文通过结合非结构时间域有限元法和L-BFGS反演算法,成功实现了考虑关断时间的地面瞬变电磁三维带地形反演.利用非结构网格的灵活性精细模拟起伏地形的变化,采用偶极子离散处理技术模拟发射源的实际形状,基于瞬时电流脉冲技术模拟关断时间的影响,最后应用L-BFGS反演算法进行模型迭代更新,完成了基于三维观测模式的地面瞬变电磁数据三维反演.理论和实测数据的三维反演结果表明地形和关断时间对反演模型影响较大,其中地形起伏导致发射线圈形状以及测点和源的空间位置关系发生变化,尤其是起伏地形和地下三维异常体相互耦合导致观测响应产生了十分复杂的畸变,在反演过程中如果利用水平地表模型强制拟合地形数据将导致反演模型中地表出现大量假异常,而且假异常不只是出现在地表,这给地质解释造成一定困难.而关断时间主要影响早期观测数据,如果利用理论阶跃波形响应拟合具有一定关断时长的观测数据将导致地表出现大量虚假异常,当关断时间较长时甚至无法找到合理的三维模型实现数据拟合.早期数据无法拟合将导致错误的模型搜索方向,进而影响深部目标体的反演效果.开发基于三维观测模式的三分量反演算法是我们未来的工作重点.
致谢特别向各位审稿人和编辑同志对本文提出的建设性意见表示感谢.

