一种基于插值技术高精度计算稀疏网格地震定位中震源轨迹的方法

赵爱华

中国地震局地球物理研究所, 北京 100081

0 引言

地震定位在防震减灾中起着十分重要的作用，不仅关乎大震救灾，而且是进行大震预测的重要基础(张国民等，2001；陈运泰，2009).大震之前，异常的地震活动范围往往很大，例如1975年的海城地震(朱凤鸣等，1982)；大震之后，余震活动的范围可达数百公里，例如2011年的日本MW9.0地震(Asano et al., 2011)；数千公里之外的事件也可能触发本地的中强震，例如2008年9月11月印度尼西亚的MW6.6地震触发了约4750 km之外的日本MW6.9地震(Lin, 2012)，因此，为准确判断震情(尽管很难)，常常需要对大尺度范围的事件进行定位.高精度的地震定位不仅是分析地震孕育环境和发生机理的基础，而且对区域、全球深部结构的研究(曾融生,1991；滕吉文等，2004；Rawlinson et al.，2010)及核爆监测(Bowers and Selby,2009)都具有重要意义.和过去相比，现代地震台网的定位能力有了很大改善，但定位精度，特别是区域和全球尺度地震定位中震源的深度精度仍有待提高(Schweitzer, 2006; Bondár and Storchak, 2011).

区域和全球尺度的地震定位(例如Xie et al.,1996；Engdahl et al., 1998)和煤炭、油气开采中的地震定位(例如Boltz et al., 2014; Bao and Eaton, 2016; 常旭和王一博，2019)，在原理上是一样的，即在地下空间中寻求一点使理论计算的和实际观测的到时(或到时差)之差最小(Thurber,1986; Moser et al.,1992)，所不同的是前者的速度模型比后者在尺度上大得多.为减小理论到时误差以提高定位精度，区域和全球的地震定位也越来越多地使用更接近实际的三维速度模型(陈棋福等，2001；Lin et al., 2007; De Kool and Kennett, 2014; Myers et al., 2015).由于三维速度模型的地震波走时难以表示成解析表达式，因此通常使用射线追踪技术进行数值求解，而模型则以网格剖分成模型单元.区域和全球地震定位中的速度模型，尺度较大，不宜以较小网格剖分，否则剖分的单元过多、走时计算量太大.再者，速度模型主要来自地震层析成像结果，而目前区域和全球尺度的地震层析成像，分辨率还比较低(例如，Kohler et al.，2003; Lin et al., 2010; Xin et al., 2019; Simmons et al., 2019)，这样，即使以较小网格剖分模型，也不会在根本上提高理论走时的计算精度.当模型以稀疏网格剖分时，由于剖分的单元尺寸较大，走时计算将变得较为复杂，例如，模型界面难以用模型单元的中心点连线近似表示，否则，会人为地产生较大的齿状断层；相邻单元中心点之间的射线路径用直线代替将可能导致较大误差.因此，对于大多数的地震定位方法而言，例如，盖革法(Geiger, 1912)、主事件法(Spence, 1980)、双差法(Waldhauser and Ellsworth, 2000)、搜索法(Prugger and Gendzwill, 1988； Kennett and Sambridge,1992；Billings，1994；Shearer,1997；Sambridge and Kennett, 2001)以及震源参数与速度结构联合反演法(Crosson, 1976; Zhang and Thurber, 2003)等，区域和全球地震定位的困难主要在于理论走时的计算，但对于地震定位交切法则不尽然.交切法基于几何思想定位，将震源轨迹交会最集中的点作为震源位置，具有稳健直观的优点(Garza et al., 1977,1979；傅淑芳和刘宝诚，1991；Pujol, 2004; 廉超等，2006)；但当速度结构较为复杂时，震源轨迹难以找到解析解(Zhao and Ding, 2007, 2009; 周建超和赵爱华，2012).因此，将传统交切法应用于高精度的区域和全球地震定位，还需要解决大尺度复杂模型中震源轨迹的求解问题.

对于复杂速度模型中的震源轨迹，目前主要有两种求解方法.第一种，以残差(理论计算的与实际观测的到时或到时差之差)绝对值较小的单元节点近似表示震源轨迹，单元节点通常取为模型单元的中心点(Zhou，1994；Font et al., 2004；Theunissen et al., 2012).这种方法，简单易行，但当模型以稀疏网格剖分时，由于模型节点的间距较大，得到的震源轨迹有较大误差.为减小误差，在稀疏网格中初步确定震源位置后，再以细网格对初步确定的震源其周围区域进行剖分，更精确地确定震源位置.这样做，虽然在一定程度上解决了问题，但无疑增加了工作量，而且实现起来也较烦琐.另外，以绝对残差较小的点表示的震源轨迹不是理论上的曲面而是厚度不均的板带，轨迹所交会的为一个区域而非一个点，即使速度模型和到时都准确.针对该问题，本文作者与合作者提出了另外一种求解震源轨迹的方法，其基本思想是：选取震源轨迹所经过模型单元的节点为轨迹参考点，以绝对残差场中连接参考点的射线路径表示震源轨迹(赵爱华等，2008，2015；赵爱华，2018).相比于第一种方法，第二种方法得到的震源轨迹更为精细，根据震源轨迹的交会情况可直观地评估定位效果，便于对观测到时进行优化组合、设计最佳的地震定位方案；不过，该种方法同样存在当模型以稀疏网格剖分时所得到的震源轨迹误差较大的问题.高精度的区域和全球地震定位，不仅范围广，而且台站多、事件量大，要求震源轨迹的计算有较高的精度和效率.

为此，本文尝试对基于射线追踪技术的震源轨迹计算方法(赵爱华，2018)进行改进，使之满足区域和全球事件定位的需要：当模型以稀疏网格剖分时，计算的震源轨迹也具有较高的精度，并且计算效率较高.虽然地震定位是一个三维问题，但为便于叙述，方法说明仍以二维模型为例.

1 震源轨迹方程

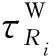
1.1 到时差约束的震源轨迹方程

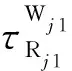
(1)

由方程(1)可得到时差残差(RDT)场FRDT：

FRDT(x;Rj1,Wj1;Rj2,Wj2)=[T(x;Rj1,Wj1)

(2)

其中，I(x)为空间单位场，其值处处为1.

1.2 到时约束的震源轨迹方程

(3)

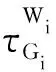
(4)

到时残差(RAT)场FRAT为

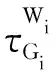
(5)

其中，I(x)为空间单位场.

值得指出的是，到时约束的震源轨迹不仅与作为约束条件的观测到时有关，还与构建发震时间场的观测到时有关.发震时间场不同，同一到时约束的震源轨迹也不同，甚至相差很大(赵爱华等，2015).

2 震源轨迹参考点的计算

对于速度结构复杂模型，震源轨迹难以准确计算，不便于进行误差分析.为此，考虑一个均匀介质模型，模型大小为150 km×90 km，介质P波和S波的速度分别为6.0 km·s-1和3.6 km·s-1(赵爱华等，2015).为考察网格稀疏时的震源轨迹计算误差，将模型剖分成较大单元，例如5 km×5 km的正方形，在其浅部布设5个地震台站Ri(13.5+(i-1)×30.0 km,-2.5 km)(i=1,2,3,…,5).设在点x0(37.5 km,-31.5 km)处，时间t0=0 s时发生地震.图1显示了台站R3处P波和S波到时差约束的震源轨迹(蓝色实线)及其残差场，图中棕色点为轨迹所经过模型单元的中心点(为便于叙述，将其称为震源轨迹节点).可以看出，在均匀各向同性介质中，同一台站P波与S波到时差约束的震源轨迹为圆形；震源轨迹节点和轨迹的理论解，有明显的偏差，这一点在图1中局部放大的图中显示得更为清楚.可以推知，当模型单元较大时，选取震源轨迹节点为轨迹参考点、以连接轨迹参考点的线作为震源轨迹会有较大误差.

易知，选取的参考点越接近实际震源轨迹，计算的震源轨迹越精确，最理想的情况是选取震源轨迹上的点即残差场中的零值点为轨迹参考点.观察图1可知，残差从震源轨迹一侧到另一侧，从正变为负或反之；沿轨迹法线方向，残差变化最快.据此，可以假定：在震源轨迹两侧附近，残差沿轨迹法线方向的变化可表征为简单的函数.若使用震源轨迹两侧法线上邻近点构建插值函数，则插值函数的零点应离实际震源轨迹较近.在计算震源轨迹之前，准确的轨迹法线方向是难以确定的.不过，根据震源轨迹在残差场中的特点，和轨迹法线相近的方向，例如法线点对方向(赵爱华，2018)却是可以确定的.法线点对由位于震源轨迹两侧的邻点组成，其方向和轨迹法线方向相差不超过45°.这样，基于插值技术计算法线点对间残差为零的点作为震源轨迹参考点，也应具有较高精度.根据这种认识，本文提出了如下计算震源轨迹参考点的算法：

图1 均匀介质中事件以同一台站P波与S波到时差约束的震源轨迹及其残差场棕色点为震源轨迹所经过模型单元的中心点；红色十字为使用插值方法计算的震源轨迹参考点；蓝色实线是震源轨迹的理论解,绿色虚线为±1.0 s的残差等值线.Fig.1 A hypocentral locus constrained with the travel time difference between the P - and S- wave at the same station and its residual field of an event in a homogeneous mediumBrown dots are nodes of the mode elements traversed by the hypocentral locus; red crosses indicate the focal locus reference points by linear interpolation. Blue lines show the theoretical solutions of the hypocentral locus; the green lines are the residual contours of ±1.0 s.

(1)组成点对

对每个模型节点，考虑其上下、左右4个邻点(三维，再加前后2个邻点)； 若存在和节点残差正负极性不同的邻点，则将这样的邻点和节点组成点对.

(2)确定法线点对

选取同一模型节点其全部点对中绝对梯度最大者为法线点对.法线点对中绝对残差较小的点更靠近震源轨迹，震源轨迹经过其所在模型单元，即该节点为震源轨迹节点.

(3)插值求解

使用法线点对及其两侧延长线上的模型节点构建残差的插值函数，选取插值函数中残差为零的点作为轨迹参考点.

需要指出的是，尽管模型节点的坐标是二维或三维的，但残差在法线点对方向上的变化是一维的，因此构建插值函数较为简单.对于法线点对A(xA,zA,RA)和B(xB,zB,RB)(其中，R为残差值)，若残差在点对AB间线性变化，则AB间残差为零的点P,其坐标为

(6)

若残差在点对AB间非线性变化，则可以用二分法求取残差为零的点.图1中，红色十字是使用线性插值方法计算的震源轨迹参考点.可以看出，计算的轨迹参考点和轨迹的理论解(蓝色实线)几乎完全重合，具有较高精度.

3 射线路径的计算

震源轨迹的参考点是离散的点，虽然可直接用于地震定位，但以其表示的震源轨迹不太形象和细密；若用线将离散的轨迹参考点连接起来，则有利于更直观地考察震源轨迹在空间的展布.由式(2)和(5)可知，震源轨迹在绝对残差场中具有近于零的低值.这样，若将绝对残差看作地震波速度的倒数(即地震波慢度)，在绝对残差最小处激发地震波，则地震波将沿震源轨迹快速传播，而在轨迹两侧传播较慢.因此，震源轨迹参考点可在绝对残差场中以射线路径连接(赵爱华等，2008).绝对残差场，非均匀性较强(参见图1)，因此，连接轨迹参考点的射线路径，应选用稳健性好的射线追踪方法计算，例如最小走时树法(Nakanishi and Yamaguchi, 1986).最小走时树射线追踪方法以构建最小走时树的方式计算地震波传播路径和走时(Dijkstra, 1959；Cao and Greenhalgh, 1993)，没有阴影区问题，计算的走时全局最小，适于复杂模型的计算；经过不断地改进和完善(Moser, 1991;王辉和常旭, 2000; Zhao et al., 2004; 赵爱华和徐涛, 2012)，计算效率也较高.当震源轨迹由多段组成时，仅将绝对残差场中全局最小的那个节点设置为射线路径初始点，计算结果将包含虚假震源轨迹；若将射线路径计算区域限制在绝对残差较小的区域，计算区域依震源轨迹的段数组成自适应地划分为若干连通区域，选取每个连通区域中绝对残差最小的点为震源点，则无虚假轨迹问题(赵爱华等，2015).鉴于根据残差极性可选取全部或几乎全部的震源轨迹节点(赵爱华，2018)，本文将选出的震源轨迹节点所在的模型单元作为射线路径的计算区域.常规的最小走时树法仅计算模型节点之间的射线路径，而不能处理非模型节点的点.注意到震源轨迹节点和计算的轨迹参考点存在对应关系，因而可采取先计算连接震源轨迹节点的射线路径、再以计算的轨迹参考点代替射线路径中震源轨迹节点的办法来计算震源轨迹.

4 模型算例

4.1 速度模型

为验证方法的适用性，将改进的震源轨迹计算方法应用于一个接近实际的速度模型.该模型以云南地区为背景，修改自遮放—宾川速度剖面(白志明和王椿镛，2004).模型速度结构如图2所示，S波与P波速度之比vS:vP为常数1∶1.73.可以看出，速度的纵向和横向非均匀性都较强；地壳与地幔之间的界面，即莫霍(Moho)面，深度变化显著.参照文献(赵爱华等，2015)做法，将模型剖分成边长为1 km的正方形单元，模型单元内速度设为常数；布设于地表的9个地震台站Ri(i=1, 2, 3…9)，深度为0.5 km,台站间距为20或30 km；将地震事件设置在点x0(130.5 km, -27.5 km)处，发震时间为t0=0 s.震源至地震台站6种震相(Pg、Sg、PmP、SmS、Pn和Sn)的到时，使用子波传播区域(控制计算精度)动态调整、效率较高的最小走时树射线追踪方法(赵爱华等，2003)计算.PmP/Pn波的射线路径，如图2中灰线所示.

对于图2中模型的事件，作者及其合作者曾计算了Pg波和Sg波其到时差和到时约束的震源轨迹(赵爱华等，2015).已有的研究表明，使用莫霍面反射波(PmP和SmS)或折射波(Pn和Sn)有利于震源深度的确定(白玲等，2003；Husebye et al, 2013; Wagner et al., 2013).关于反射波和折射波的震源轨迹，目前研究得还较少.因此，本文将重点考察这类震相到时或到时差约束的震源轨迹.

图2 以云南地区为背景的速度模型(修改自白志明和王椿镛,2004)红色十字为震源位置；黑色倒三角形为地震台站；灰线为地震反射/折射波射线路径.Fig.2 A velocity model set in Yunnan area (modified from Bai and Wang, 2004)The red letter “+” indicates the hypocenter; black inverse triangles denote the seismic stations; gray lines show the ray paths of reflected or refracted seismic waves.

4.2 到时差约束的震源轨迹

全部9个台站两两组合，对于某个震相，总计可产生36个到时差.由Pg波到时差约束的震源轨迹可知，其中有些到时差约束的震源轨迹在方位分布上是非常接近的.因此，计算所有台站组合的震源轨迹是不必要的.为便于和Pg波对比，本文计算了相同台站组合、PmP/Pn波到时差约束的震源轨迹，计算结果如图3a所示.图例线上的数字对“i-j”表示震源轨迹所对应的台站组合为Ri和Rj.可以看出，震源轨迹在震源附近有良好的方位分布，能很好地约束震源位置，这和Pg波到时差约束的震源轨迹(赵爱华等，2015)相似；但和后者仅交会于震源点不同，在莫霍面之下、约在震源点的对称位置还有较集中的交会.震源轨迹在莫霍面发生急剧方向变化可能源于界面两侧(上：反射波/折射波；下：直达波)的走时场具有不同的分布特征.

相同台站PmP/Pn波与SmS/Sn波到时差约束的震源轨迹显示在图3b中，轨迹旁边的数字“i”表示轨迹所对应的台站为Ri.可以看出，轨迹在震源附近有很好的方位分布；在震源处，近台(例如R3)的轨迹以水平分布为主，对震源深度有较好的约束，而远台(例如R1)的轨迹则以垂直分布为主，可较好地约束震源的水平位置.值得注意的是，近台(例如R3和R4)的震源轨迹为在地下闭合的曲线.可以证明，若莫霍面水平、地壳为均匀各向同性介质，则同一台站(位于地表)反射纵、横波到时差约束的震源轨迹(反射界面之上部分)为圆形，圆心在台站之下2倍地壳厚度处.因此，对于近台，震源轨迹可能不会出露于地表，这点和直达纵、横波到时差约束的震源轨迹不同.

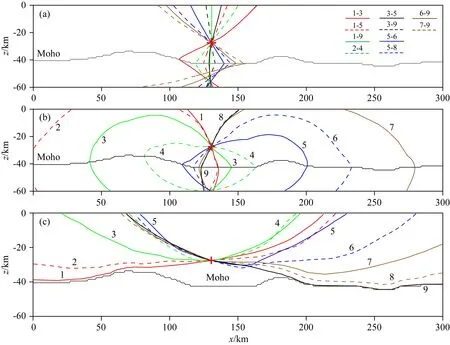
图3 图2中事件以到时差约束的震源轨迹(a) 不同台站PmP波到时差； (b) 相同台站PmP波与SmS波到时差; (c) 相同台站PmP波与Pg波到时差.不同颜色和线型的曲线表示不同震源轨迹，其旁边的数字“i”或数字对“i-j”表示震源轨迹以台站Ri或台站对Ri-Rj的到时差约束.Fig.3 Hypocentral loci constrained with arrival time differences for the event in Fig.2(a) Traveltime differences between PmP waves at different stations; (b) Traveltime differences between PmP and SmS waves at the same stations; (c) Those between PmP and Pg waves at the same stations. Curves in different colors and styles represent different hypocentral loci and their sideward figures “i” or figure pairs “i-j” imply that they are constrained with the arrival time differences from stations Ri or station pairs Ri-Rj.

相同台站直达纵波(Pg)和反射/折射波(PmP/Pn)到时差约束的震源轨迹如图3c所示，轨迹旁边的数字“i”表示轨迹所对应的台站为Ri.可以看出，无论是近台(例如R3、R4和R5)还是远台(例如R1、R2和R9)，轨迹在震源处均以水平分布为主，似乎对震源深度都有很好的约束.根据以前的研究(赵爱华等，2015)可知，震源轨迹约束震源位置的能力，不仅与轨迹在震源附近的方位分布有关，还与轨迹的稳定性有关.轨迹越稳定，受扰动影响越小，对震源位置的约束越强.在绝对残差场中，震源轨迹越稳定，其所在的“峡谷”(将绝对残差看作高程)越窄陡；反之亦然.图4显示了图3c中近台R3和远台R9所对应的震源轨迹及其绝对残差场.为清晰显示震源轨迹，对绝对残差做了取对数处理.易见，相同台站PmP/Pn波与Pg波到时差约束的震源轨迹其所在的“峡谷”，近台的为陡窄的“V”形，而远台的为半侧宽缓的反“L”形.这说明，前者轨迹较为稳定，对震源深度有较强约束；后者轨迹稳定性较弱，较小的扰动就可使其形态或位置发生显著变化，虽然在震源处以水平分布为主，但对震源深度的实际约束则较弱.这与地震定位中“近台约束强、远台约束弱”的经验相符.

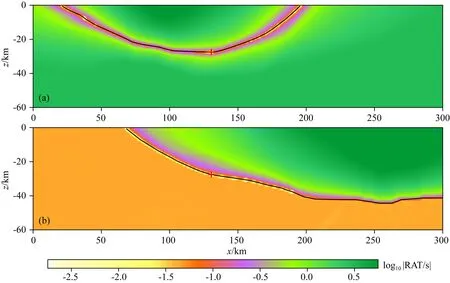
图4 图3c中近台(上)和远台(下)震源轨迹的残差场Fig.4 Residual fields of hypocentral loci for near (up) and far (down) stations in Fig.3c

4.3 到时约束的震源轨迹

全部台站PmP/Pn波到时约束的震源轨迹如图5a所示.和到时差约束的震源轨迹(图3a)相比，到时约束的震源轨迹在震源附近的方位分布略窄，不过有两条轨迹在震源点具有较大的方位夹角，因此仍能较好地约束震源位置.当以全部台站PmP/Pn波和Pg波到时构建发震场时，PmP/Pn波(蓝线)和Pg波(绿线)到时约束的震源轨迹显示在5b中.可以看出，增加Pg波到时后，震源轨迹与之前的相比，方位分布大大改善.较为全面的方位覆盖使震源位置得到有力约束；更多条震源轨迹约束震源，有利于减少随机干扰对定位结果的影响.

在地震定位实践中，事件被近台和远台都记录到是较理想的情况.微小地震，激发的能量较弱，往往难以被远台记录到而仅能用近台定位.研究表明，近台在约束震源水平位置方面起着关键作用(Bondár et al, 2004).大震之后在震源附近沿发震构造布设流动台阵其目的即是用近台对余震活动进行更好地监测.图5c和5d显示了近台(R2-R6)PmP/Pn波及其与Pg波到时约束的震源轨迹.可以看出，当仅有近台时，PmP/Pn波单独约束的震源轨迹在震源处的分布方位上更加不均，除了有一条近水平分布外，其余则都集中地分布于垂直方向很窄的方位范围内；PmP/Pn波和Pg波共同约束的震源轨迹，则和全部台站的情形类似，在震源处的方位分布全面且较均匀，对震源位置有很好的约束.

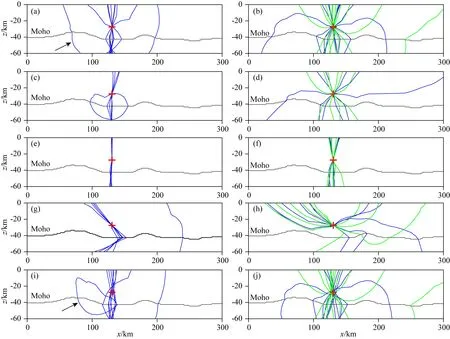
图5 图2中事件不同观测情况以到时约束的震源轨迹(a)和(b) 所有台； (c)和(d) 近台； (e)和(f)远台； (g)和(h) 右侧台； (i)和(j) 扰动到时. 左边图仅使用PmP波到时；右边图使用PmP和Pg波到时，其中蓝线和绿线分别对应PmP和Pg波. 红色“+”为震源位置.Fig.5 Arrival time constrained hypocentral loci of the event in Fig.2 for different observations(a) and (b) complete observation; (c) and (d) near observation; (e) and (f) far observation; (g) and (h) right-side observation; (i) and (j) disturbed arrivaltimes. Hypocentral loci in the left subfigures involve only PmP-wave data; those in the right ones involve both PmP- and Pg-waves, where they are shown in blue and green respectively for PmP and Pg waves. The red “+” indicate the true hypocentral position.

在地震台网稀疏地区，很多时候仅有远台可用于定位.为模拟缺少近台的定位情形，仅保留距震源较远的5个台站：R1、R2、R7—R9.PmP/Pn波及其与Pg波到时约束的震源轨迹分别如图5(e，f)所示.PmP/Pn波单独约束的震源轨迹在震源处均近垂直分布，可很好地约束震中位置，但难以约束震源深度；增加Pg波到时后，轨迹在震源处的分布方位：范围略有加宽，但仍以垂直方向为主.这表明，缺少近台，即使联合使用PmP/Pn波和Pg波也难以很好地约束震源深度.

在区域台网的地震定位中，事件常常位于台网之外.为模拟该种情形，仅保留右侧5个台站R5-R9.PmP/Pn波到时约束的震源轨迹如图5g所示.震源轨迹在震源处以和水平方向成约135°(以逆时针方向为正)的方位成束分布，对震源位置约束较弱.增加Pg波到时信息后，震源轨迹(图5h)在震源处的方位分布得到显著改善，对震源位置特别是震源深度的约束显著加强.

震相到时误差是影响定位精度的关键因素之一.采用互相关技术(例如Akram and Eaton, 2016)或人工智能技术(例如Ross et al., 2018;Wang et al., 2019)可大大提高到时拾取精度，但若环境噪声较大，准确地拾取到时仍较困难.为模拟到时拾取存在误差情况，使用FORTRAN编译器中的随机函数对PmP/Pn波和Pg波的理论到时加以扰动，两种波的扰动幅度均为±0.5 s，扰动均方值分别为0.321 s和0.356 s.PmP/Pn波单独约束、PmP/Pn波和Pg波联合约束的震源轨迹分别如图5(i,j)所示.可以看出，当观测到时有误差时，震源轨迹不再交会于震源点，而是交会成一个小的区域.图5i中闭合的轨迹(箭头所指)明显偏离震源点，而且形态发生了较大变化(参见图5a中箭头所指轨迹), 表明其稳定性可能不是很强.和单独震相到时约束的震源轨迹相比，两种震相到时联合约束的震源轨迹其交会最密集的点更接近实际震源位置.

和Pg波到时约束的震源相比(参见赵爱华等，2015)，PmP/Pn波到时约束的震源轨迹在震源处的方位分布是类似的；不同的是，后者除了在震源处有较集中的交会外，在莫霍面之下也有密集交会的点.轨迹在莫霍面发生急剧方向变化可能主要源于界面上下的地震波走时场具有不同分布特征.

5 讨论

5.1 计算误差

由计算过程可知，震源轨迹的计算精度决定于轨迹参考点的精度.轨迹参考点越接近实际的震源轨迹，以连接参考点之射线路径表示的震源轨迹越精确.对于复杂介质模型(例如图2中模型)，难以找到震源轨迹的理论解.为此，本文以图1中均匀介质模型中事件的震源轨迹(其解析解为标准的圆形)来例，分析模型单元尺寸及插值方法对震源轨迹参考点计算精度的影响.模型单元边长d=1、3、5、7、9 km时，使用不同方法计算轨迹参考点的结果如表1所示.可以看出：对于选用震源轨迹所经过模型单元中心点作为轨迹参考点即震源轨迹节点法，轨迹参考点的误差和单元边长d基本成正比，最大值和平均值分别约为d/2和d/4；插值法轨迹参考点的精度虽然总体上也是随着单元边长d的增大而降低，但比震源轨迹节点法的高几十(线性插值)到几百倍(抛物插值和三次样条插值)；当模型单元较大时，插值函数次数越高，计算的轨迹参考点误差越小：以d=9 km为例，线性(1次)插值法、抛物插值(2次)法和三次样条(3次)法轨迹参考点的误差最大值分别为0.110、0.027和0.015 km；但这并不意味着使用更高次的插值函数计算轨迹参考点的效果会更好.高次插值函数存在震荡现象，求取函数法线点对间的零值点(可能有多个)较为复杂，并且可能由于插值函数对震源轨迹附近区间残差的变化表征得更差而使得其零值点离实际震源轨迹更远.

在表1中，三次样条差值法d=3 km时的轨迹参考点误差为0.004 km,比其d=7 km时0.003 km的误差还要大，似乎不合理.为解释该现象，考察了图1中残差沿震源轨迹法线方向的变化，如图6所示.轨迹法线为水平，显示的区间从A(103.5 km,-31.5 km)至B(112.5,-31.5 km).图中红色虚线为连接点A和B的直线.可以看出，残差在震源轨迹附近沿法线方向近似为线性变化,但有波动.这种波动有可能使得以震源轨迹两侧较近的点(对应较小模型单元)比以轨迹两侧较远的点(对应较大模型单元)构建三次样条插值函数、函数的零值点离实际轨迹更远.

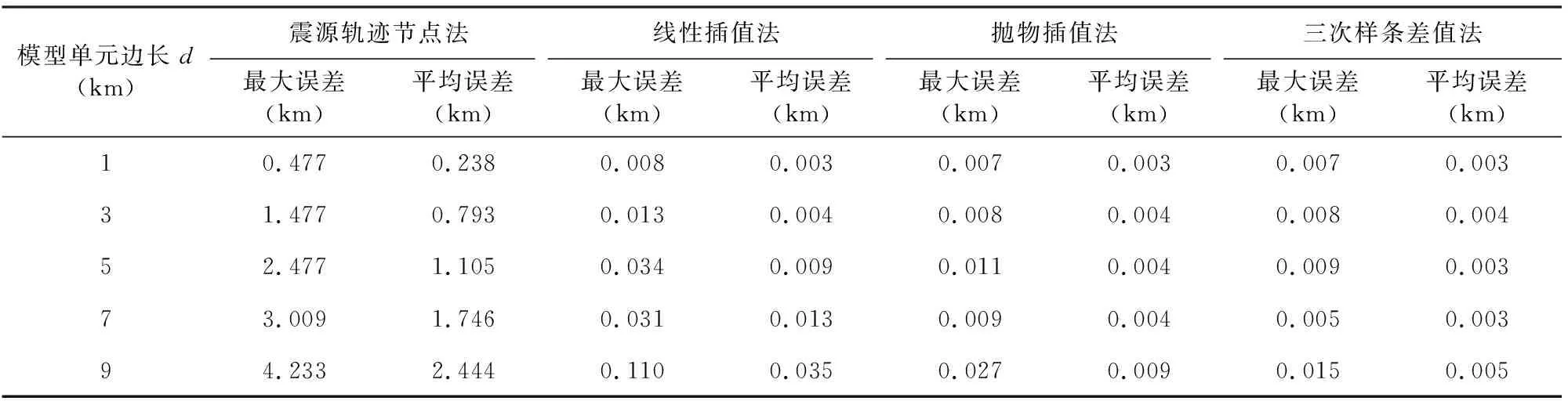
表1 不同方法计算图1中震源轨迹参考点的精度比较Table 1 Accuracy comparison of different methods for calculating the hypocentral locus in Fig.1

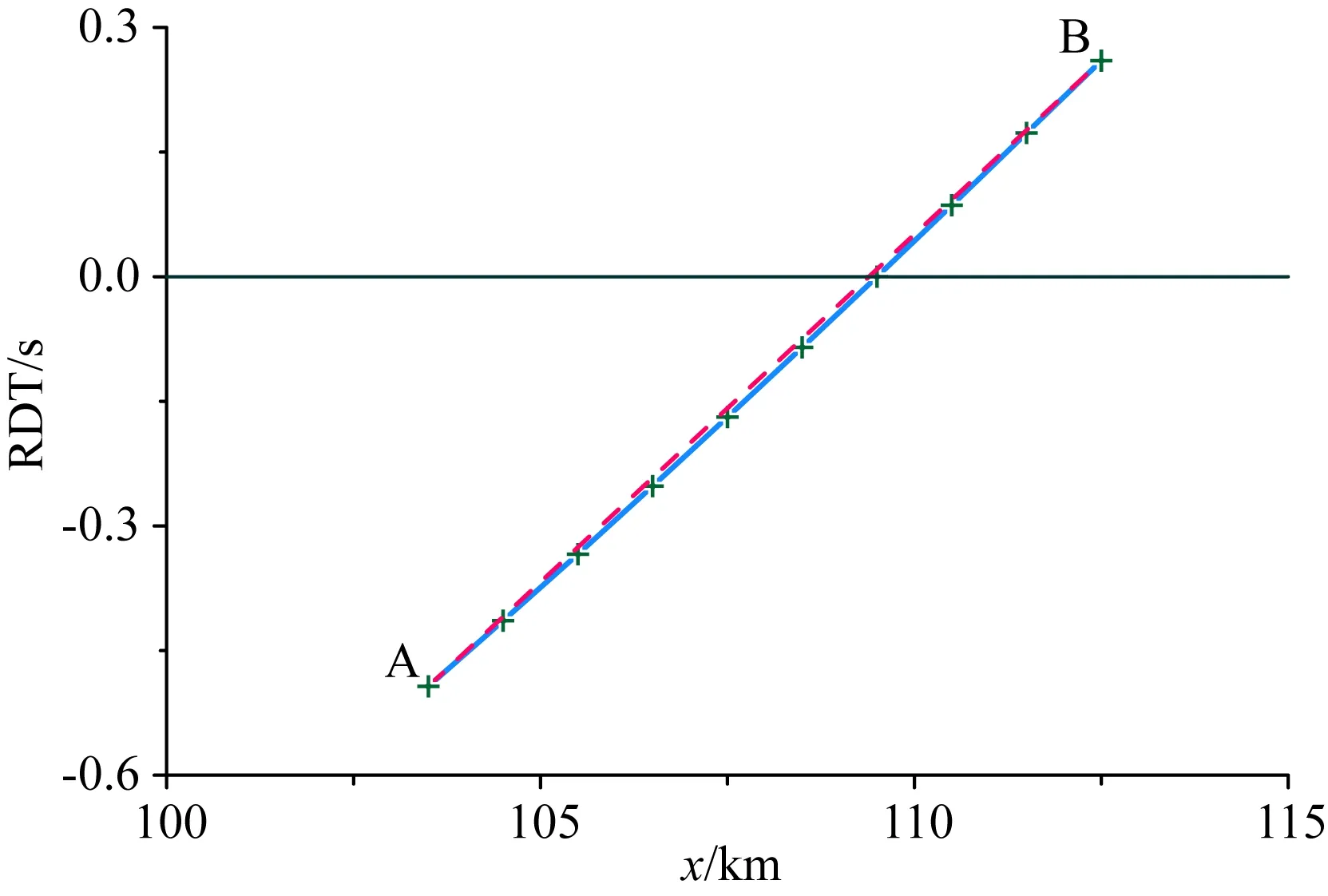
图6 图1中到时差残差沿震源轨迹法线A(103.5,-31.5)B(112.5,-31.5)方向的变化Fig.6 Variation of traveltime difference residual along the normal A(103.5,-31.5)B(112.5,-31.5) of the hypocentral locus in Fig.1

5.2 计算效率

由表1可以看出，粗网格时使用插值法计算轨迹参考点可达到细网格时震源轨迹节点法的精度.以最简单的线性插值为例，d=9 km时其轨迹参考点的精度比震源轨迹节点法d=1 km时的精度还高.对于给定模型，d=1 km时的模型单元数是d=9 km时的81倍(二维)或729倍(三维).在震源轨迹计算中，地震波走时场的计算最为费时，计算时间和模型单元数成正比.这意味着，使用新的轨迹参考点计算方法可使用于计算地震波走时场的时间大大减少，尽管后者的计算与地震事件无关，对于稳定区域仅需1次，但对于尺度较大的三维模型或当地震台站较多时，这种减少的效果还是非常显著的.

在选取震源轨迹节点的基础上，基于插值技术求取法线点对间残差为零的点作为轨迹参考点需要花费额外的计算时间.表2列出了不同插值法计算轨迹参考点所额外花费的CPU时间，CPU时间使用编程语言FORTRAN中的函数timef计量.需要指出的是，程序连续重复运行多次，每次得到的CPU时间并不完全一致，表中所列是出现次数最多的结果.尽管数据不是很精确,但仍可以看出，使用插值法计算轨迹参考点额外花费的时间不是很多，以d=1 km时为例，线性、抛物、三次样条三种插值法计算轨迹参考点所额外花费的时间分别为0.007 s、0.039 s和0.045 s，和常规方法(以震源轨迹节点为参考点)计算震源轨迹的时间(0.117 s)相比，分别增加5.98%、33.33%和38.46%，和地震波走时场的计算时间(单次为3.09 s)相比，增加的比例则更低.随着单元尺寸的增大，由于震源轨迹节点个数减少，使用插值法计算轨迹参考点所额外花费的时间越来越少.

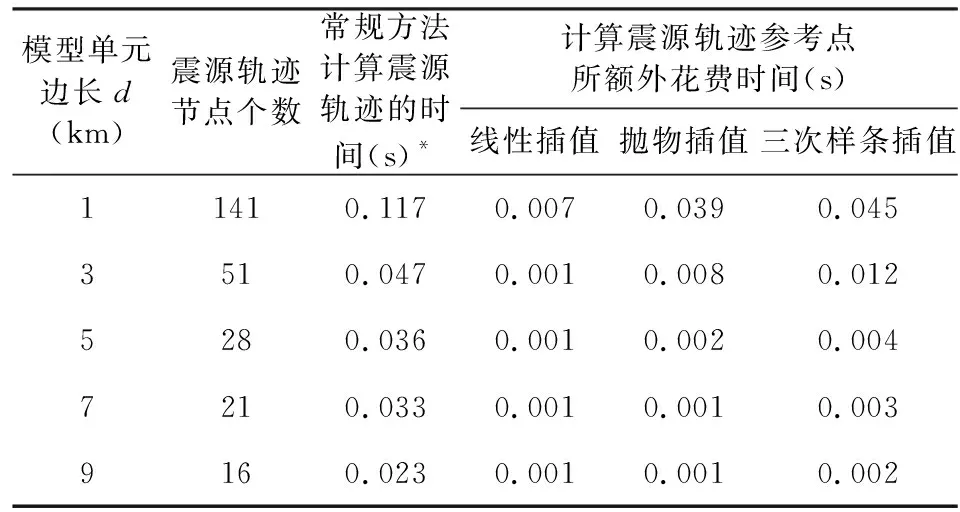
表2 震源轨迹参考点计算对计算效率的影响Table 2 Effect of the calculation of FLRPs on the efficiency

在射线路径计算部分，需要将路径中模型节点替换为计算的轨迹参考点.由于操作简单，而且当使用稀疏网格时，需要替换的节点较少，因此这部分所花费的时间微乎其微，对轨迹的计算效率影响不大.

5.3 算法的实用性

和理论实验相比，实际的地震定位有更多的不确定性因素，例如地下的速度结构难以准确获知、拾取的震相到时存在或多或少误差等.计算真实事件的震源轨迹可较好地检验本文算法的实用性.实际的地震存在于三维空间.对于三维速度模型，根据残差正负极性可选取全部或几乎全部的震源轨迹法线点对(赵爱华，2018)；法线点对虽然在三维空间分布，但其上的残差变化是一维的，这样，使用一元的插值方法仍可高精度地计算出三维残差场中的零值点作为震源轨迹参考点.因此，本文所提出的震源轨迹计算方法在理论上是适用于三维速度模型的.尽管如此，为便于展示和分析，本文仍以二维模型中真实事件的计算为例，说明算法的实用性.

在二维空间中考察震源轨迹的分布，震中和台站应位于同条直线.文献(赵爱华等，2015)提供了较为符合这一要求的实例.地震发生在华北地区，北京数字遥测地震台网(北京台网)的测定结果为：震中位于117.42°E、39.61°N，震源深13 km，发震时间为2012年8月26日7时13分34.3秒.该地震具有良好的观测方位覆盖，并且有近台(CAD台，震中距仅3km)控制，定位到时残差较小，可以认为定位结果可靠.震中和三个台站(从南至北依次为EWZ台、CAD台和XAZ台)基本位于同条直线(见赵爱华等，2015中图6).根据三个台站的Pg波和Sg波走时，参照华北东部地壳模型(滕吉文等，1979)，赵爱华等(2015)构建了一个水平层状均匀的速度模型，模型由三层介质组成、尺度为60 km×35 km.该模型对于北京台网确定的震源位置和震相到时，EWZ台、CAD台和XAZ台的Pg波和Sg波走时残差(理论走时与观测走时之差，单位为s)分别为：(-0.08，0.40)、(-0.06，-0.35)和(0.05，0.05).他们使用0.1 km×0.1 km的网格计算了三个台站Pg波和Sg波的走时场.和地震波走时场相比，震源轨迹的计算需要更多内存；地震波走时场的空间采样率对计算轨迹的完整性与精细性影响不大.为此，当计算震源轨迹的程序可能因内存超限而不能运行时，他们对得到的地震波走时场进行了粗网格(0.2 km×0.2 km)重采样以完成计算.使用其粗网格采样的走时场和北京台网确定的震相到时，本文计算了真实事件的震源轨迹，计算结果如图7所示，对应不同台站或台站组合的震源轨迹以不同彩色线表示.可以看出：不同台站Pg波到时差约束的震源轨迹(图7a)交汇得较为集中，交汇点和震源位置仅略有偏差；同一台站Pg波与Sg波到时差约束的震源轨迹(图7b)交汇成一个区域，走时残差越小的到时其约束的震源轨迹离震源点越近；Pg波到时约束的震源轨迹(图7c)不仅交会得较集中，而且对震源位置有较好的方位覆盖，其中台站CAD所对应的轨迹(绿色线)在震源处近水平分布，对震源深度有较强约束；Pg波与Sg波到时约束的震源轨迹(7d, 彩色实线对应Pg波，彩色虚线对应Sg波)和图7b中的轨迹类似，交汇得不太集中，但交汇区包含震源位置，可能意味着使用较多的震源轨迹进行定位有助于减少随机扰动对定位结果的影响.Pg波单独约束的震源轨迹(图7a和7c)比Pg波与Sg波共同约束的震源轨迹(图7b和7d)交汇得更为集中，这可能与Pg波走时残差小、Sg波走时残差较大有关.当震源轨迹交汇成区域时如何确定震源位置，是使用震源轨迹进行地震定位需要解决的另外一个关键问题.

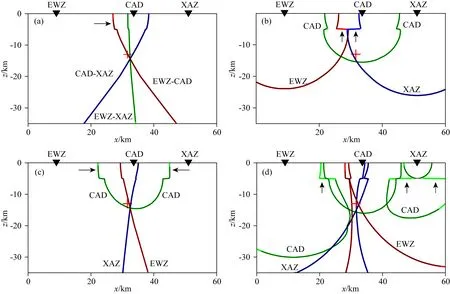
图7 华北地区2012年8月26日ML4.2地震的震源轨迹(a) P波到时差约束； (b) P和S波到时差约束； (c) P波到时约束； (d) P波和S波到时约束. 黑色线为赵爱华等(2015)计算结果， 彩色线为本文计算结果(详情见正文). 倒三角形为地震台站, 红色十字为北京台网所定震源位置在台站连线上的投影.Fig.7 Hypocentral loci of the 26 August 2012 ML4.2 earthquake in North China(a) Constraint of arrival time differences between P waves; (b) Constraint of those between P and S waves; (c) Constraint of P-wave arrival times; (d) Constraint of P- and S-wave ones. Hypocentral loci in black come from Zhao et al. (2015) and those in colors (red, green and blue) are results in this study (see text for details). The inverse triangles represent the seismic stations and the red crosses indicate the projection of the hypocenter determined by Beijing Seismic Network to the station line.

对比文献(赵爱华等，2015)的计算结果(图7中黑色线)，可以发现本文计算的震源轨迹更为完整，如图7中水平箭头所指示部分.轨迹完整性的差异与轨迹参考点的选取或计算方法不同有关.赵爱华等(2015)在绝对残差场中使用“削皮”法选取轨迹参考点，选取的参考点可能不都是震源轨迹节点，为此去掉较短路径使计算轨迹精细的修饰会损害轨迹的完整性.本文计算的轨迹参考点与选取的轨迹节点一一对应，在残差场中基于残差正负极性选取轨迹节点，选出的点不但全是轨迹节点而且包含全部或几乎全部的震源轨迹节点，因而计算的震源轨迹相当完整.

图7中两种计算结果另外一个显著不同之处是早先计算的震源轨迹存在间断，如垂直箭头所指示部分.为分析计算轨迹中断原因，图8显示了中断最严重的震源轨迹(图7d中对应CAD台Pg波到时、以绿色实线表示的轨迹)的走时残差场.可以看出，在残差变化缓慢的区域，以线性插值计算的轨迹参考点(棕色点)和绘图软件以克里克插值法(空间采样率亦为0.2 km×0.2 km)得到的0.0 s残差等值线(绿色线)符合得相当好; 在残差变化较剧烈的区域，两者不太相符(见图8a).将图8a中计算轨迹左边中断附近的残差场(紫色箭头所指区域)放大(图8b)，易见计算的轨迹参考点位于正残差节点(红色菱形)和负残差节点(蓝色菱形)之间，并且靠近残差绝对值较小一侧的节点，这说明以线性插值方法计算的残差零值点较为准确.轨迹参考点不间断的分布表明相应区段的震源轨迹为连续分布.计算轨迹中断部分，总有某侧、有时甚至双侧的相邻节点绝对残差值大于0.2 s(见图8b中以空心菱形表示的节点).这样，按照文献(赵爱华等，2015)的方法，为保证计算轨迹的完整性，轨迹参考点选取区域的阈值RFLRP和射线路径计算区域的阈值RFL均要大于0.2 s.若RFL>0.2 s，则射线路径的计算区域将包括图8a中部两段轨迹之间的区域，使得单个连通区域内包含两段轨迹、产生虚假轨迹(连接两段轨迹之间的射线路径).为防止产生虚假轨迹，赵爱华等(2015)将RFLRP和RFL取为较小的值(0.05 s)，使计算的震源轨迹产生中断.本文算法可在整个模型区域中选取震源轨迹节点，只要将RFLRP取得足够大(例如0.5 s)，就可选出全部或几乎全部的轨迹节点，将选出的轨迹节点所在单元设置为射线路径的计算区域，使得每个连通区域仅包含一段震源轨迹，即使两段轨迹之间区域的绝对残差很小也不会产生虚假轨迹，从而可很好地同时兼顾计算轨迹的完整性与精细性.

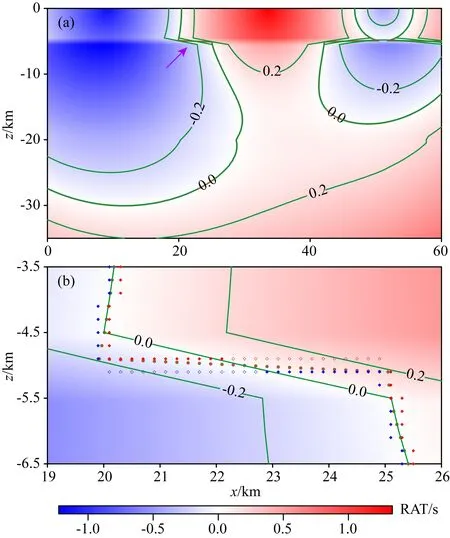
图8 图7d中绿色实线震源轨迹(对应CAD台站P波走时)的残差场(a)及其局部放大图(b)棕色点为使用线性插值计算的震源轨迹参考点;菱形为震源轨迹两侧相邻的模型节点(间距0.2 km),其中蓝色的表示残差小于0,红色的表示残差不小于0, 空心的表示残差绝对值大于0.2 s,实心的表示残差绝对值不大于0.2 s. 绿色线为到时残差等值线(单位为秒).Fig.8 Entire (a) and enlarged partial (b) residual fields of the hypocentral locus (responding to the P- wave arrival time at station CAD) shown as solid green lines in Fig.7dBrown dots are focal locus reference points by linear interpolation. Diamonds indicate model nodes (spaced 0.2 km apart) adjacent to the hypocentral locus, where the blue are negative and the red are nonnegative residual values; the empty are bigger and the solid are not bigger than 0.2 s of the absolute residual. Green lines are contours of arrival time residual (in second).

真实事件的计算结果表明：本文算法具有良好的稳健性，即使震源轨迹所在区域残差变化剧烈，也能得到可靠结果；对震源轨迹组成的段数有较强的自适应性，即使分开的两段轨迹之间的区域绝对残差很小也不会产生虚假轨迹，可很好地同时兼顾计算轨迹的完整性与精细性；计算参数易于设置且不必随震源轨迹几何形态而频繁修改, 适于大批量事件的自动处理.由此可知，本文基于插值技术计算震源轨迹的方法具有较强的实用性.

6 结论

本文提出的基于插值技术计算残差零值点为参考点的震源轨迹计算方法，不仅保持了常规方法(以震源轨迹节点为参考点)的优点，如适用于复杂模型计算、对震源轨迹的组成段数及稳定性没有限制等，而且即使剖分模型的网格较为稀疏，计算的震源轨迹也具有很高精度.以稀疏网格剖分模型，可大大减少模型单元数量，从而相应地减少了震源轨迹计算(特别是其中最为费时的地震波场计算)所需的计算机内存和CPU时间，对于大尺度模型和台站较多的台网，效果更为显著.稀疏网格中震源轨迹快速高精度计算的实现，使利用震源轨迹对区域和全球范围内的地震事件进行快速高精度的定位成为可能.

数值实验表明：莫霍面反射纵波(PmP)对地壳中事件震源的约束和直达纵波(Pg)相似，但与后者不同的是，前者的震源轨迹除了较集中地交会于震源点附近外，在莫霍面之下也有较集中的交会；同一台站PmP-Pg波到时差约束的震源轨迹在震源附近以水平分布为主，对震源深度有较好约束；联合使用PmP-Pg波到时可更好地约束震源位置、减少随机干扰的影响；相比于远台，近台对震源位置特别是震源深度有更好的约束.

致谢中国地震局地球物理研究所的吴庆举研究员对本项工作给予了支持、房立华研究员在真实事件数据获取方面给予了帮助；美国普林斯顿大学的刘前程博士提出了建设性意见；作者同时也感谢评审专家的中肯评述.