波动方程初至波多信息联合反演方法
张建明, 董良国, 王建华
同济大学海洋地质国家重点实验室, 上海 200092
0 引言
在山地地震勘探中,建立一个相对精确的近地表速度模型是后续地震资料处理和解释的关键步骤之一.包含有直达波、折射波和回转波的地震初至波,最先被检波器记录到,并且通常能量较强,容易识别,因此,在构建近地表速度模型时应用最为广泛.
初至波中的不同信息(如走时、相位、振幅、包络、波形等)对速度参数的敏感性和反演能力不同,在速度反演时对初始速度模型的依赖程度不同,反演的收敛性也不同.其中,地震波走时随速度变化具有更好的线性特征,它是近地表速度建模中最常用的一种信息.初至波走时层析方法可以基于不同的正演引擎,如射线追踪(Zhu et al., 1992)、Eikonal方程求解(Sei and Symes, 1994, 1995;Taillandier et al., 2009;Waheed et al., 2014; Waheed et al., 2016),也可以基于波动方程进行初至波走时反演(WTI)(Luo and Schuster, 1991)等.
然而,由于地震波走时主要受到大尺度速度变化的影响,走时层析方法往往只能得到分辨率较低的宏观速度模型,有时无法满足实际地震勘探对地下介质精细刻画的要求.为了充分利用初至波中的动力学信息,进一步提高近地表速度建模的精度,有学者提出了初至波波形层析成像(EWT)方法(Sheng et al., 2006),这种方法是全波形反演(Lailly, 1883;Tarantola, 1984;Pratt et al., 1998)在近地表建模方面的一种应用.EWT可以利用包含在地震初至波中的全部信息,从理论上讲,EWT比走时层析具有更高的反演精度,但由于地震波传播的复杂性,使用波形残差构造目标函数,必然导致反演的强烈非线性,在初始模型远离真实模型、观测和模拟的初至波走时差大于1/2周期时会产生周波跳跃而致使EWT反演陷入局部极值(Virieux and Operto, 2009),子波未知以及噪声干扰等一系列实际问题也严重阻碍了波形反演的实用化进程.因此,在现阶段的实际速度建模中,波形反演还无法完全取代传统的走时层析技术,而是应该根据勘探的不同阶段,采取分阶段、分尺度逐渐提高反演精度的策略(Bunks et al,. 1995; 董良国等, 2013, 2015).在此指导思想下,在反演的初期阶段,应充分利用初至波的走时信息(Luo and Schuster, 1991; Zhang and Toksöz,1998)或相位信息(Choi and Alkhalifah, 2013)来更新近地表速度模型的长波长分量,得到宏观的背景速度场;然后逐渐利用地震波的低中频信息进一步提高反演精度,例如利用初至波包络反演近地表速度的方法(EEI)(敖瑞德等, 2015);最后使用波形信息,得到高精度的速度模型.
这种常规的走时、包络和波形串联反演策略虽然也可以得到较高精度的速度模型,但是,在后期利用初至波的包络或波形的反演阶段,由于缺少走时信息的约束,在初至波的包络或波形匹配时会产生一定程度的周波跳跃(Liu and Zhang, 2017).因此,Liu和Zhang(2017)提出了一种近地表速度结构建模的走时、包络和波形的联合反演方法,在不同的反演阶段,每一次迭代过程中走时、包络和波形信息都同时被利用.然而,在Liu和Zhang(2017)所提出的方法中,走时匹配部分采用的是基于射线追踪的层析方法;包络和波形匹配部分基于波动方程正演模拟.这导致他们所提出的联合反演方法有3个不足之处:(1)在每一次迭代中,射线追踪和波动方程正演需要分别计算;(2)走时匹配基于射线理论,使得反演方法的精度受到射线理论的高频假设制约,致使他们所提出的联合反演方法难以适用于复杂速度变化的情况;(3)走时匹配部分依赖于精确的走时拾取,在数据质量不佳的情况下,拾取走时必然耗费巨大的人力和时间.
为此,本文提出了一种统一基于波动方程正演引擎的初至波走时、包络和波形联合反演方法(Joint traveltime, envelope and waveform inversion, JTEW)来建立近地表速度模型.该方法统一使用波动方程正演引擎计算正传波场和伴随波场,正传波场可以同时应用于走时、包络和波形的匹配,伴随波场应用于梯度的计算.使用初至波形的互相关可以自动提取模拟和观测初至波的时差,无需再进行额外的射线追踪.通过权重因子可以分阶段自动调节不同信息的比例,自然地实现分阶段、多尺度反演,为初至波波形反演的实用化提供了一种有效途径.
1 方法原理
JTEW方法同时匹配模拟和观测的地震初至波的走时、包络和波形,通过权重因子调节三种信息的比例.定义JTEW的目标函数为
(1)
其中,ω1和ω2分别是走时和包络的权重因子,1-ω1-ω2为波形的权重因子,且0≤ω1≤1,0≤ω2≤1,JTEW的权重因子选择是一个重要的课题,将在下一节中详细讨论.Jt、Je和Jw分别为走时、包络和波形的目标函数值,因为三者通常不是一个数量级,所以我们对它们进行了归一化处理,其中Jt0、Je0和Jw0为归一化因子,它们分别表示第一次迭代的走时、包络和波形的目标函数值.
在JTEW的目标函数(1)中,走时、包络和波形各自的目标函数分别定义为
(2)
其中,Δτ(xs,xr)为对应于炮点xs和检波点xr的观测和模拟初至波的走时差;E和E0分别表示观测与模拟的初至波形的包络, ln表示取对数;Δu(xr,t;xs)=u(xr,t;xs)-u0(xr,t;xs)为观测与模拟初至波的波形残差.其中理论模拟波场u(x,t;xs)满足下列点震源子波为f(t)的波动方程:
(3)
针对上述JTEW的目标函数(1),基于伴随状态法(Plessix, 2006),通过正传波场与伴随波场的零延迟互相关就可以得到目标函数(1)的梯度(具体推导过程见附录A):
+u′e(x,t;xs)+u′w(x,t;xs)]}dt,
(4)
这里,c(x)为空间位置x处的速度.u′t(x,t;xs)、u′e(x,t;xs)和u′w(x,t;xs)分别为走时、包络和波形的伴随波场,与之对应的伴随震源分别为
f′t(xr,t;xs)=
(5)
(6)
f′w(xr,t;xs)=
(7)

令
u′all(x,t;xs)=u′t(x,t;xs)+u′e(x,t;xs)
+u′w(x,t;xs),
(8)
为总的伴随波场,它是由三种信息联合的复合伴随震源f′(xr,t;xs)以波动方程正演引擎反向传播得到,其中
f′(xr,t;xs)=f′t(xr,t;xs)+f′e(xr,t;xs)
+f′w(xr,t;xs).
(9)
这样,在每次迭代中只需要使用波动方程(3)对上述(9)式的复合伴随震源f′(xr,t;xs)进行一次反向传播,将得到的伴随波场u′all(x,t;xs)与震源端的正传波场u(x,t;xs)进行零延迟互相关(公式4)即可得到JTEW目标函数的梯度.然后通过线性搜索算法可以很方便地获得一个优化的步长αn,这样就可以利用下面(10)式的局部优化算法进行速度迭代,得到最终的速度反演结果.
(10)
另外,由于(5)、(6)、(7)式的计算量与波场模拟相比几乎可以忽略不计,因此,本文提出的JTEW方法与单独采用波形反演的计算量基本相当.
从以上方法可以看出,本文的JTEW方法弥补了Liu和Zhang(2017)联合反演方法的不足,主要优势体现在以下三个方面:(1)在每一次迭代过程中,统一使用波动方程正演引擎计算正传波场和伴随波场进行梯度计算,无需再进行额外的射线追踪正演计算;(2)走时、包络和波形匹配都是基于波动方程正演模拟结果,提高了方法在复杂介质情况下的适用性;(3)通过初至波形互相关自动提取模拟和观测初至波的时差,无需人工拾取走时,省时省力.
2 联合反演权重因子的选择策略
在JTEW方法中,权重因子的选择对反演结果有很大的影响.下面通过对目标函数性态分析,提出了一种合理有效的可变权重因子选择策略.
为了检验不同初至波信息的目标函数的性态,本文设计了如图1所示的模型和观测方式,在地表的中间放炮,模型的底部接收,共501个检波器,相邻检波器间距10 m.真实速度v=2500 m·s-1,速度扰动范围为1500~3500 m·s-1,计算出不同速度摄动时的目标函数如图2所示.

图1 模型和观测方式示意图Fig.1 Schematic diagram of the model and survey geometry
图2a表明,波形目标函数(绿线)凸性最差,说明波形反演是一个强烈的非线性问题,只有初始模型足够接近真实模型时,目标函数才能正确收敛到全局极值.包络目标函数(蓝线)凸性较好,但是当初始模型距离真实模型较远时,特别是当速度偏低时,目标函数对速度变化不敏感,速度很难向正确的方向更新.走时目标函数(红线)具有很好的凸性,但是同时它对速度变化的敏感性最低,因此,走时反演通常只能得到低分辨率的速度模型.

图2 目标函数性态(a) 不同信息目标函数的性态; (b) 不同权重系数时的联合反演目标函数.图a中,绿线:波形反演的目标函数; 蓝线:包络反演的目标函数; 红线:走时反演的目标函数; 黑线:联合反演的目标函数(w1=0.3,w2=0.4).图b中,洋红线:w1=0.7,w2=0.2; 蓝线:w1=0.3,w2=0.5; 红线:w1=0.1,w 2=0.6; 绿线:w1=0.1,w 2=0.3; 黑线:w1=0.05,w 2=0.1.Fig.2 Objective function behavior(a) The behavior of different information objective functions; (b) The JTEW objective functions with different weighting factors. Green line: EWT objective function; blue line: EEI objective function; red line: WTI objective function; black line: JTEW objective function, where w1=0.3, w2=0.4. Magenta line: w1=0.7, w 2=0.2; Blue line: w1=0.3, w 2=0.5; Red line: w1=0.1,w 2=0.6; Green line:w1=0.1, w 2=0.3; Black line: w1=0.05, w 2=0.1.
图2b表明,初至波JTEW目标函数可以兼具三者的优点,在反演中可以通过调整不同信息的权重因子得到凸性不同、和对速度敏感性不同的目标函数.总体来说,走时权重从大变小,波形权重从小变大,联合反演目标函数凸性变差而对速度的敏感性变强.根据这个特征,在反演初期阶段设置较大的走时权重,主要更新背景速度模型;随着迭代的进行,逐渐减小走时权重而先增大包络的权重,更新模型的中波数成分;最后减小走时和包络的权重,增大波形权重更新模型的高波数成分,从而自然地实现分阶段、多尺度反演,最终得到高分辨率的反演速度模型.这也为本文联合反演权重因子的选择策略的设计提供了依据.
依据上述分析,本文设计了一种全自动的可变权重因子的联合反演策略(图3),总共15个反演阶段,三个固定权重因子对应一个反演阶段.在第一个反演阶段,走时、包络和波形的权重分别为1、0、0,当该阶段的目标函数不再下降时,自动跳到第二个反演阶段,新阶段的权重因子按图3自动调节,以此类推,直到最后一个反演阶段结束.整个反演过程中走时的权重因子从1指数衰减到0,波形权重因子与走时权重因子的变化是反对称的,即从0指数增大到1,其余部分是包络的权重因子.

图3 联合反演权重因子系数Fig.3 Weighting factors in JTEW
这样设计权重因子,充分考虑到了走时与速度之间的弱非线性关系,使得JTEW在反演的初期阶段能够获得一个可靠的宏观速度模型.在后续的反演阶段,走时与速度之间的这种弱非线性不会被丢弃,而是作为包络和波形的约束加载在目标函数中,并且逐渐减小其比重而加大波形信息的权重,以便在联合反演的后期阶段,波形信息被充分利用,从而自动实现分阶段、多尺度反演,最终得到一个高精度的近地表速度模型.
在本文的JTEW方法中,也可以根据实际情况灵活地设计不同的权重策略而将反演分成多个阶段,表1展示的是几种不同反演策略的权重设置及其实际意义.可以看出,无论是单信息反演、固定权重联合反演或者是常规串联反演,均是可变权重联合反演的一个特例.下文中的JTEW若没有特别说明,均是指可变权重的联合反演.联合反演最佳权重策略该如何设计(如设置多少个反演阶段,走时、包络和波形的权重因子是何种变化形式,第一个和最后一个阶段的权重值分别设置多大,等等),还有待进一步优化.
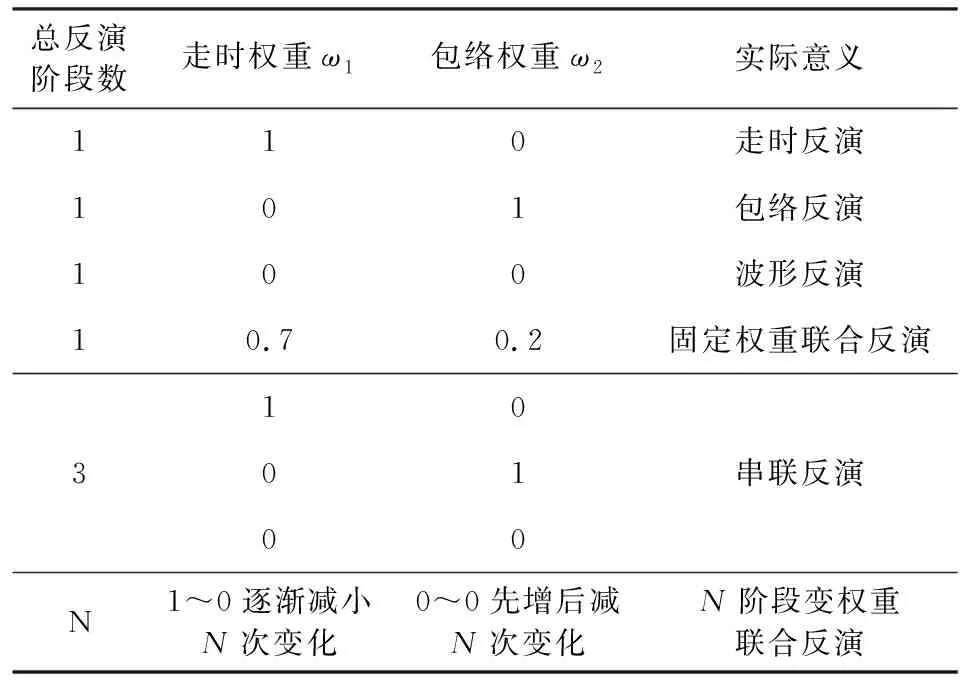
表1 不同反演策略权重因子表Table 1 Weighting factors of different inversion strategies
3 理论模型试验
利用横向速度周期变化模型和Foothill模型两个数值实例,说明本文所提出的可变权重联合反演方法相较于单信息反演、串联反演以及固定权重联合反演的优势.
(1)横向速度周期变化模型试验
模型的横纵向网格数为501×51,水平和垂直网格间距均为10 m.在试验过程中,采用有限差分法正演模拟地震波,震源为主频15 Hz的雷克子波,101炮均匀分布于地表,炮间距50 m,每炮501个检波器在地表均匀分布,相邻检波器间距10 m.真实模型如图4a所示,初始模型是速度值为2500 m·s-1的常速初始模型.使用相同的常速初始模型,进行了五种不同反演方法的数值试验,包括波动方程初至波走时反演(Luo and Schuster, 1991)、初至波波形反演(Sheng et al., 2006)、固定权重因子(ω1=0.7,ω2=0.2)联合反演、走时+波形变权重因子联合反演、以及JTEW反演.
由于常速初始模型与真实模型相差较大,初至波波形反演结果明显地陷入了局部极值(图4b),反演结果完全失真.初至波走时反演只能得到分辨率较低的背景速度模型(图4c).与固定权重因子联合反演结果(图4e)相比,走时+波形变权重因子联合反演结果(图4d)和JTEW反演结果(图4f),不仅有效更新深度更大,而且在近地表分辨率更高.这是因为在固定权重因子联合反演的整个迭代过程中,各部分的权重保持不变(ω1=0.7,ω2=0.2),导致走时、包络和波形三部分信息只有权重最大的走时信息被充分利用,波形信息利用不足,若减小走时的权重,又会造成反演的不稳定.而JTEW反演方法则可以通过改变不同信息的权重,在反演的不同阶段强调利用不同的信息,自然地实现多尺度反演,最终得到分辨率更高、有效更新深度更大的反演速度模型.值得说明的是,尽管只利用走时和波形两种信息进行变权重因子联合反演,也得到了较好的反演效果(图4d),但包络信息的加入,使得JTEW方法得到了精度更高的反演结果(图4f).

图4 横向速度周期模型及不同方法反演结果(a) 真实速度模型; (b) 初至波波形反演结果; (c) 走时反演结果; (d) 走时+波形变权重联合反演结果; (e) 走时+包络+波形固定权重因子联合反演结果; (f) 走时+包络+波形变权重因子联合反演结果.Fig.4 Lateral periodic velocity model and inversion results with different inversion methods(a) True velocity model; (b) EWT inversion result; (c) WTI inversion result; (d) WTI+EWT Joint inversion result with variable weighting factors; (e) JTEW inversion result with fixed weighting factors; (f) JTEW with variable weighting factors.
图5显示的是150 m和200 m深度处的水平速度曲线,可以看出,JTEW反演结果(红线)总是比波形反演(绿线)和固定权重联合反演结果(蓝线)更加接近真实模型(黑实线).这表明,JTEW方法在反演初期阶段充分利用了走时信息,为后续反演阶段提供了更加稳定的初始模型,而在联合反演的后期阶段更加充分地利用了波形信息,有效提高了速度模型的分辨率.可见,与单信息反演和固定权重联合反演相比,JTEW方法在反演精度方面具有明显的优势.

图5 不同深度处的反演速度模型的水平速度剖面(a) 150 m深度; (b) 200 m深度. 黑色实线和虚线分别表示真实模型和初始模型;蓝色和绿色实线分别表示固定权重因子联合反演和波形反演结果;红线表示变权重因子联合反演结果.Fig.5 Horizontal velocity profiles of the inversion velocity model at (a) y=150 m and (b) y=200 mThe black solid line and the dashed line represent the true model and the initial model, respectively; The blue and the green solid line represent the JTEW result with fixed weighting factors and EWT result, respectively; The red line represents the JTEW results with variable weighting factors.
图6显示了不同反演速度模型与真实模型第101炮的初至波波形拟合情况.可以看到,对应于初始模型的理论波形(蓝色)与“观测”波形(红色)匹配较差(图6a),在图6a中的局部区域A和B,“观测”波形和理论波形相位差异超过了1/2周期.对应于初至波波形反演结果(图4b)的初至波,小偏移距的初至波波形与“观测”初至波波形拟合较好,但是大偏移距的初至波波形仍然拟合较差(图6b).这是由于初始模型的估计偏离了真实模型,导致反演陷入了局部极值.
固定权重的联合反演结果较初至波波形反演结果的波形拟合有了大幅提升,但仍然存在一定残差(图6c),而JTEW得到了比较完美的波形匹配效果(图6d).这是因为固定权重的联合反演考虑了走时的信息,非线性程度降低.然而,固定权重的联合反演只强调利用三种信息中权重因子比较大的走时信息,导致权重值小的波形信息不能被充分利用.JTEW则能够在反演初期阶段充分利用走时信息反演得到较光滑的宏观速度模型,在反演后期期阶段充分利用波形信息提高模型的分辨率.从上面的波形匹配结果也可以看出,JTEW方法可以最大程度拟合“观测”数据,最终提高了速度反演的精度.

图6 不同模型模拟的第101炮初至波形与观测初至波形的拟合情况(a) 初始模型; (b) 波形反演模型; (c) 固定权重联合反演模型; (d) 变权重联合反演模型. 红色为观测初至波形;蓝色为不同反演结果对应的正演初至波形.Fig.6 The 101th shot waveform of (a) initial model; (b) EWT inversion model; (c) JTEW inversion model with fixed weighting factors and (d) JTEW inversion model with variable weighting factorsThe red line is the observed waveform; The blue line is the forward waveform corresponding to different inversion results.
(2)Foothill模型试验
复杂Foothill模型横纵向网格数为1255×100,网格间距20 m.地面均匀激发126炮,每炮最多401个检波器均匀分布在地表,最大偏移距为4 km.正演模拟采用基于纵向坐标变换的起伏地表地震波模拟方法,其中第65炮的完整波形及反演所用的初至波波形如图7所示.
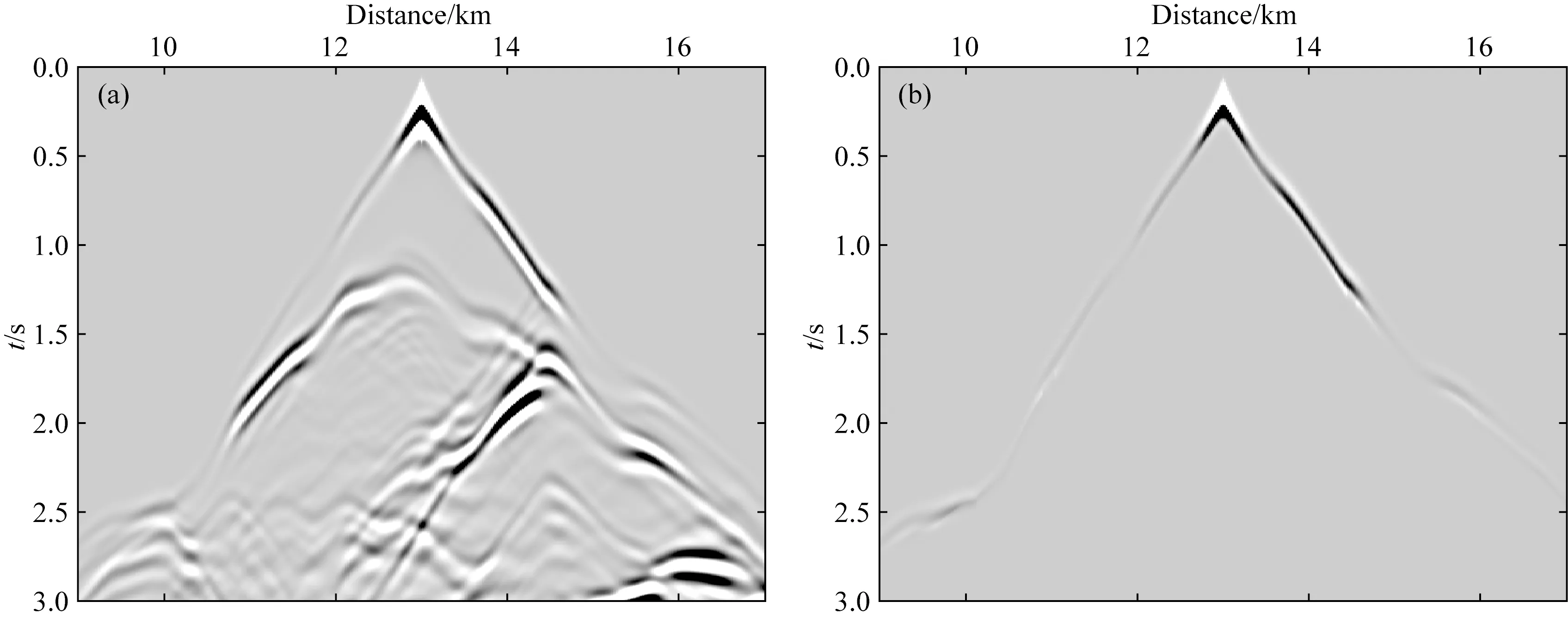
图7 Foothill模型第65炮“观测”记录以及反演所用的初至波(a) 完整波形; (b) 反演使用的初至波波形.Fig.7 Waveform of the 65th shot for Foothill model(a) Full waveform; (b) First arrival waveform used in inversion.
采用相同的常梯度初始速度模型(图8b),进行了四种初至波反演方法的对比试验,包括波动方程初至波包络反演、初至波波形反演、走时+包络+波形串联反演、以及走时+包络+波形变权重因子联合反演.
初至波波形反演结果(图8c)和初至波包络反演结果(图8d)都比较差,在图9的地下不同深度的速度曲线上,初至波波形反演结果(蓝线)和初至波包络反演结果(绿线)都是在初始模型(水平黑虚线)附近抖动,这是由于初始模型与真实模型相差较大,致使波形和包络反演均陷入了局部极值,模型没有得到有效更新.采用相同的常梯度初始模型(图8b),尽管走时+包络+波形串联反演也得到了较理想的反演结果(图8e),但本文提出的JTEW方法得到的反演结果精度更高(图8f和图9中的红色曲线)更接近于实际模型,说明了多信息、分阶段JTEW反演相对于单信息反演具有明显的优越性.
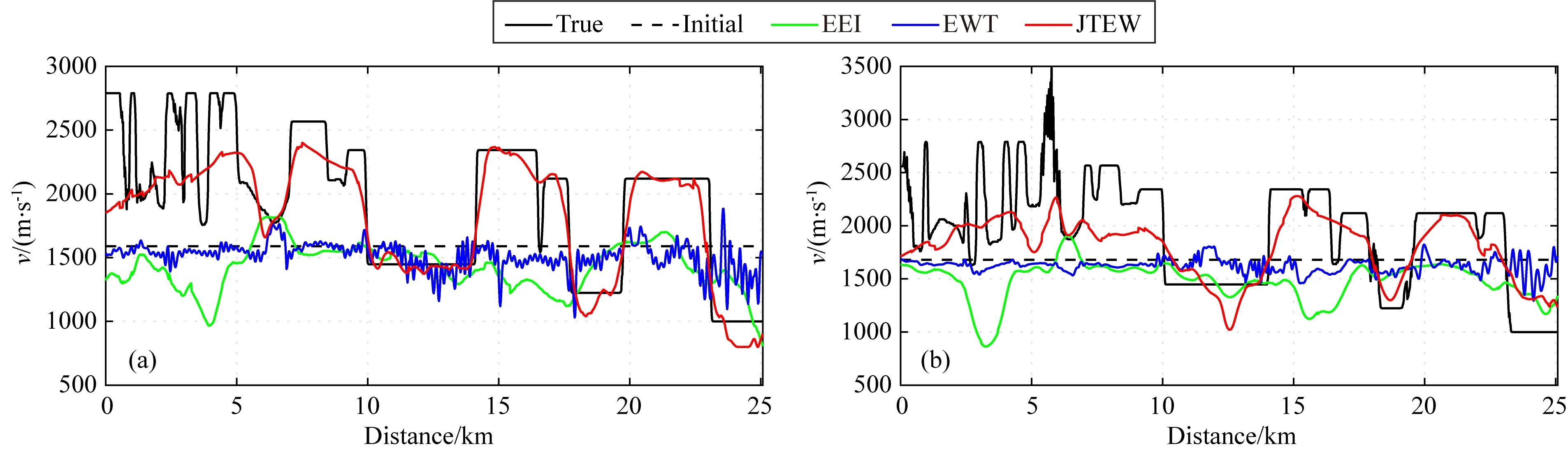
图9 地表下不同深度处的反演速度模型的速度剖面(a) 地表下200 m; (b) 地表下400 m. 黑色实线和虚线分别表示真实模型和初始模型;蓝色和绿色实线分别表示波形反演和包络反演结果;红线表示联合反演结果.Fig.9 The velocity profiles of the inversion velocity model at (a) 200 m and (b) 400 m below the surfaceThe black solid line and the dashed line represent the true model and the initial model, respectively;The blue solid line and the green solid line represent the single EWT and EEI results, respectively;The red line represents the JTEW result.
另外,目标函数下降曲线(图10a)显示,在走时+包络+波形串联反演的前120次迭代过程中,在走时目标函数值(红线)下降的同时,包络(黑线)和波形(蓝线)的目标函数值并不是持续下降,而是在一些局部出现了增大的现象(第30次迭代附近).第120次走时反演迭代结束后,包络和波形目标函数值下降的同时,走时目标函数值却又出现了升高的现象(图10a中第120~320代),我们称之为走时目标函数的漂移现象.这说明在走时+包络+波形串联反演过程中,走时反演阶段结束后,走时信息本来得到了较好的匹配,然而在后期的包络和波形反演过程中则放弃了走时信息,致使包络和波形反演过程中缺少了走时信息的约束,波形匹配变好的同时走时匹配变差.图10a中的这些现象,均说明多信息串联反演无法同时较好地匹配走时、包络和波形信息.

图10 目标函数下降曲线(a) 串联反演; (b) 联合反演.Fig.10 Decrease of objective function with iterations for (a) sequential inversion and (b) JTEW
而在联合反演过程中,走时、包络和波形目标函数值均持续下降(图10b).这是由于在联合反演后期的迭代过程中都使用走时信息作为包络和波形的约束,使得波形匹配变好的同时走时匹配也变好.因此,变权重因子联合反演可以有效缓解走时目标函数漂移问题,这也是联合反演较串联反演的优势所在.
图11显示了不同反演模型与真实模型之间初至波互相关提取的走时残差.通过对比我们可以发现三个现象:
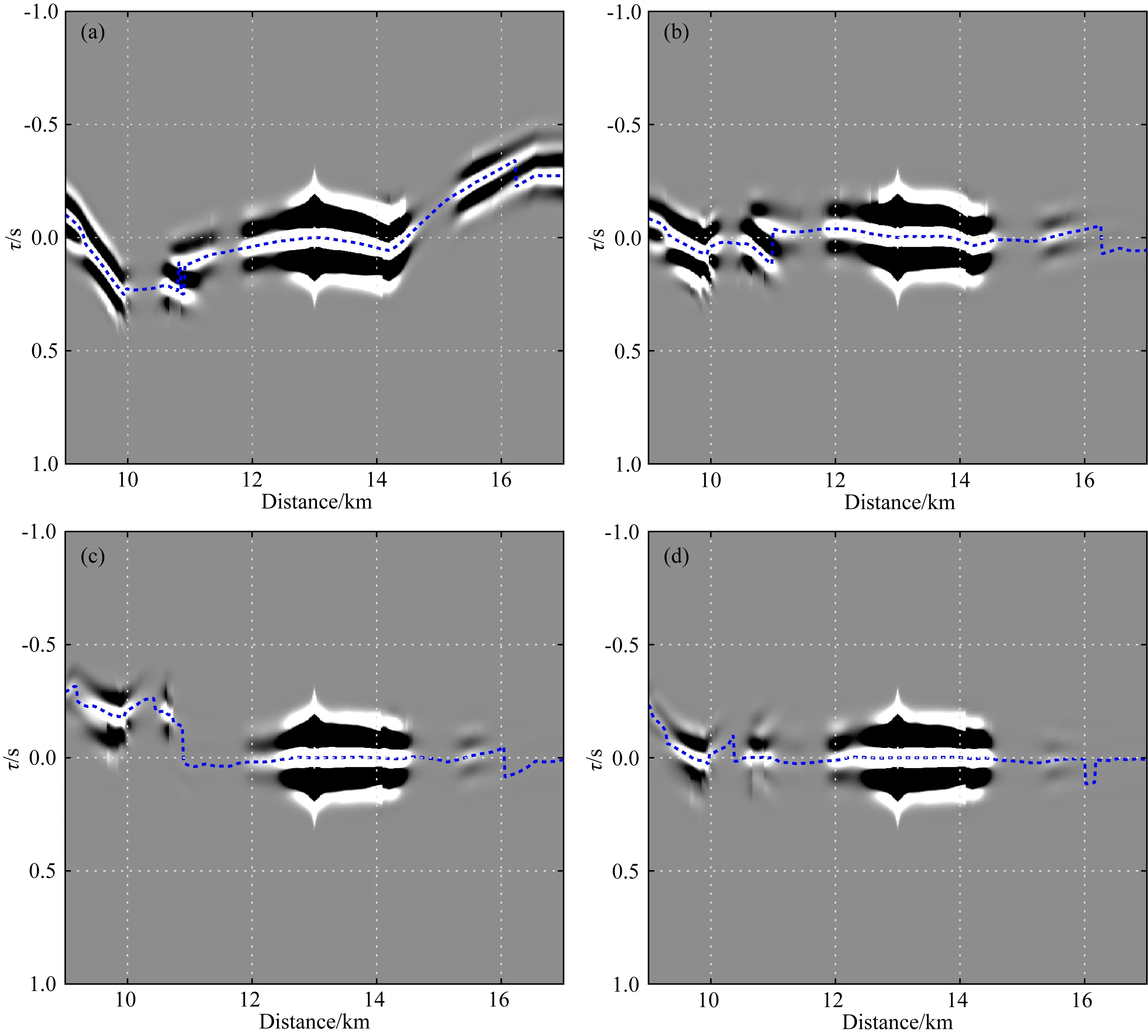
图11 在不同反演结果上模拟的第66炮初至波和“观测”初至波的互相关函数(a) 初始模型; (b) 走时反演; (c) 走时+包络+波形串联反演; (d) 走时+包络+波形联合反演.Fig.11 The cross-correlation function of the first arrival wave and the observed first arrival wave simulated by the different inversion results of the 66th shot(a) Initial model; (b) Travel time inversion; (c) Travel time, envelope, and waveform sequential inversion; (d) JTEW inversion.
(1)对比图11a和图11b发现,经过初至波波动方程走时反演,互相关函数的极大值更加靠近零值,说明经过波动方程走时反演后初至波走时信息已经得到较好的匹配.
(2)对比图11b和图11c发现,基于走时反演模型,再进行包络和波形反演,互相关函数极大值在某些位置(特别是远偏移距)反而偏离零值,说明从走时反演模型出发,串联反演中的包络和波形反演速度模型的某些位置(例如图8e红色箭头所指位置)错误更新,造成速度反演结果对走时的预测变差.
(3)对比图11c和图11d发现,基于JTEW反演结果模拟的初至波和“观测”初至波的互相关函数的极值基本在零值附近,说明在联合反演过程中,由于走时信息的约束,波形匹配变好的同时走时匹配也变得更好.走时残差对比说明了联合反演可以同时使走时、包络和波形匹配变好,充分体现了联合反演较串联反演的优势.
4 实际资料测试
选择某工区的一条二维测线试验联合反演的实际效果.该测线共有712炮,相邻炮间距约50 m.每炮最多384道,道间距20~30 m,最大偏移距为4800 m.其中,第480炮原始地震数据和拾取的初至走时(蓝线)如图12所示.
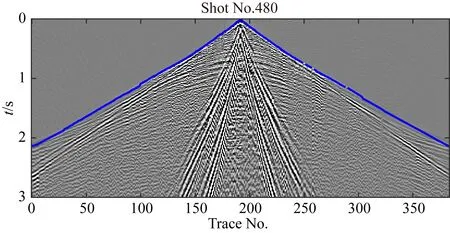
图12 实际地震资料第480炮原始记录Fig.12 The original field data record of the 480th shot
首先对数据进行了必要的预处理,包括异常道的剔除、地震数据三维至二维的转换、4~30 Hz的带通滤波等.根据初至斜率,初步估算一个平均的地表速度值,并据此设计了如图13a所示的常梯度初始速度模型,其中地表速度为1800 m·s-1,模型的最底部速度为2280 m·s-1.然后,将不依赖子波的JTEW方法应用于该测线,并将近地表反演结果与伴随状态法初至波走时层析(AST)反演结果进行对比.
在JTEW反演过程中,我们使用包络互相关提取观测初至波与模拟初至波的时差,以便尽可能地克服噪声对初至波时差的影响.整个模型剖分为1574×101个网格,网格间距25 m×10 m.AST与JTEW反演分别迭代了65次和44次,反演结果分别见如图13b和图13c.相比于AST反演得到的宏观模型(图13b),在靠近地表以及某些的深部JTEW反演结果的分辨率更高一些.由于初始速度模型不够准确,根据初始模型计算的初至走时(图14a蓝线)在远偏移距处与拾取的走时差别比较大(图14a红线),而根据JTEW最终反演的速度模型计算的理论走时与拾取走时的误差明显减小(图14b).同时,利用JTEW最终反演的速度模型模拟的初至波与实际观测的初至波拟合良好(图15).

图13 速度模型(a) 初始模型; (b) 伴随状态法走时层析迭代65次; (c) 联合反演迭代44次的反演速度模型.Fig.13 Velocity model(a) Initial model; (b) The 65th Invertion velocity model of AST; (c) The 44th Invertion velocity model of JTEW.
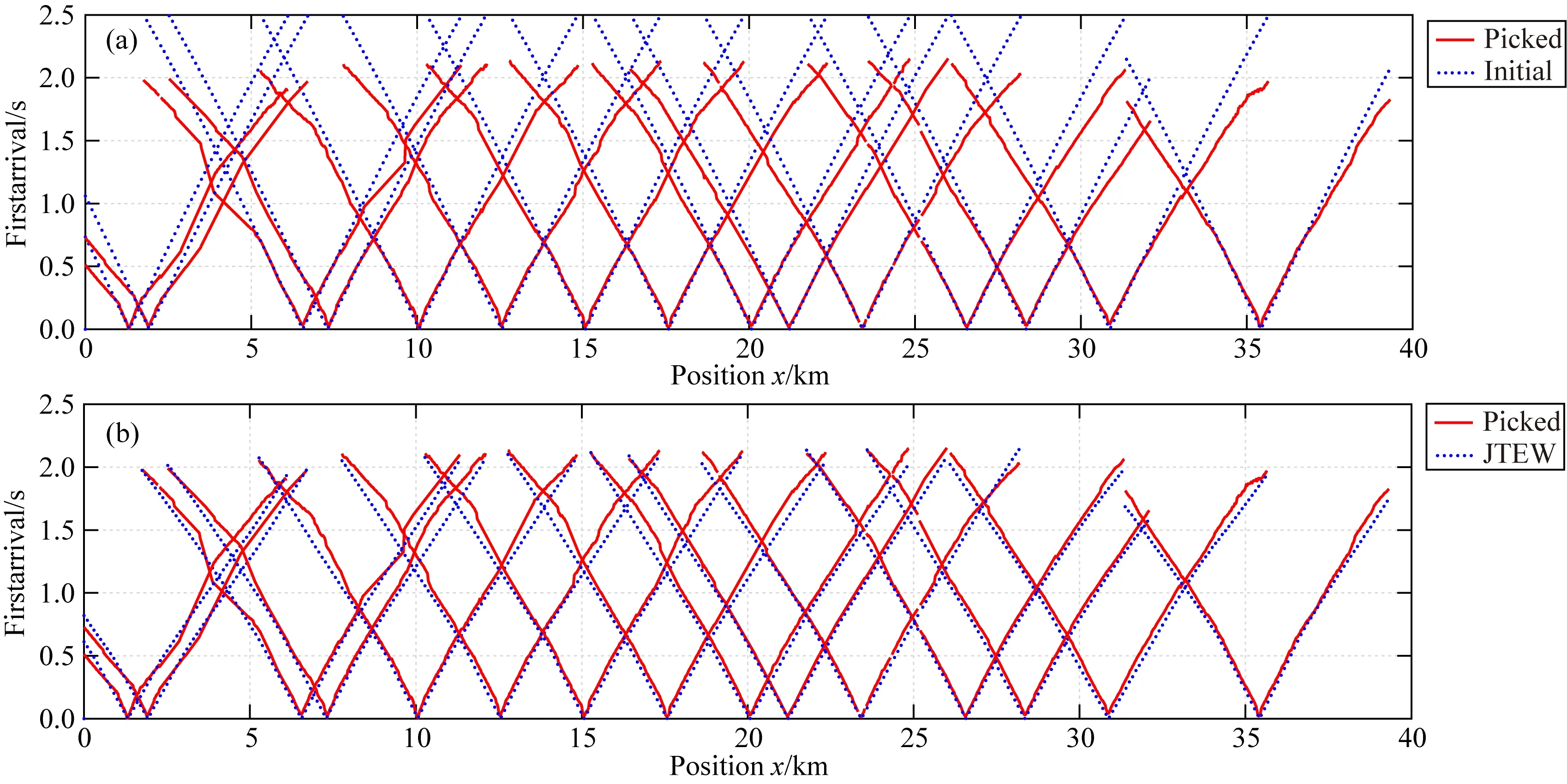
图14 (a)初始模型和(b)联合反演模型的计算走时(蓝点)与拾取走时(红线)Fig.14 The calculated traveltime (blue dot) and picked traveltime (red line) on (a) initial and (b) JTEW model.
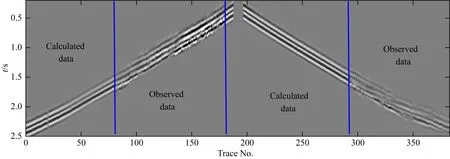
图15 第700炮实际初至波与联合反演反演模型模拟的初至波拟合情况Fig.15 Comparison between the observed and the calculated early waveform on JTEW model of the 700st shot
尽管JTEW结果的叠加剖面(图16b)与走时反演结果的叠加剖面(图16a)相比,剖面质量并没有本质的改善(深度域剖面存在明显的不同,构造形态也会有差别,因为两种方法反演的速度模型图13b和图13c存在较大的差异),但同相轴连续性还是得到了一定程度的提高(见黑色框部分),JTEW反演结果的分辨率也更高一些,这都说明了JTEW方法提高了该测线近地表速度建模的精度.

图16 (a)走时层析与 (b)联合反演结果叠加剖面对比Fig.16 Comparison of stacked profiles between (a) traveltime inversion and (b) JTEW
5 结论
本文提出的基于波动方程的初至波多信息联合反演方法(JTEW)在统一波动理论的框架下,分阶段、分尺度地考虑利用地震初至波的不同信息,有效地提高了近地表速度建模的精度.综合理论分析和两个数值算例以及一条二维测线实际地震资料处理结果,证明了提出的JETW方法的有效性.
(1)基于统一的波动方程正演引擎,一次正演得到的波场可同时用于走时、包络、波形反演梯度的计算,无需额外的射线追踪,提高了反演效率.
(2)走时、包络和波形匹配部分都是基于波动方程正演引擎,克服了射线理论中高频假设的限制,提高了方法在复杂地质情况下的适用性.
(3)模型复杂时,在串联反演过程中,走时的目标函数会发生漂移现象(本质上是周波跳跃问题).本文提出的JTEW方法可以一定程度上缓解这个问题.
(4)在初始速度模型较差的情况下,单独使用包络或波形反演容易陷入局部极值.本文提出的初至波JTEW方法,可分阶段综合利用初至波的走时、包络和波形信息,有效地降低反演对初始模型的依赖,提高近地表速度模型的反演精度.
(5)初至波波动方程单信息走时反演、包络反演、波形反演、以及固定权重联合反演和串联反演方法,均是本文所提出的JTEW方法框架下的一种特殊情况,通过选择不同的权重策略,即可灵活地实现不同的反演方法.
附录A 联合反演梯度推导
时间域声波方程为
L[u(x,t;xs)]=δ(x-xs)f(t),
(A1)
其中,xs是震源位置,u(x,t;xs)空间位置x处的波场,L为声波算子
(A2)
其中,c(x)为地下空间位置x处的速度.
传统全波形反演的目标函数一般定义为模拟数据和观测数据残差的L2泛函:
(A3)
利用伴随状态法(Tarantola,1984;Plessix,2006)可以求出梯度表达式.
(A4)
其中u′(x,t;xs)为伴随源fw(xr,t;xs)=u(xr,t;xs)-u0(xr,t;xs)的反传波场.
在地震初至波包络反演中,目标函数定义为包络对数残差的L2泛函:
-ln(E0(xr,t;xs))]2dt,
(A5)
基于伴随状态法可以推导出包络反演的伴随源为(Chi et al., 2013,2014;Wu et al.,2014;敖瑞德等,2015):
fe(xr,t;xs)=
在波动方程走时反演中,目标函数定义为相对走时差的L2泛函(Luo and Schuster, 1991):
(A7)
Δτ(xs,xr)为对应于炮点位置xs和检波点位置xr的观测初至波和模拟初至波的走时残差.该走时残差是通过互相关函数的最大值自动拾取的,即:
(A8)
其中,T为观测初至波和模拟初至波的最大时差.借助连接函数的概念(Luo and Schuster,1991),可以推导出波动方程走时反演的伴随源:
(A9)
在JTEW方法中,目标函数中同时匹配地震初至波的走时、包络和波形信息.三种信息的伴随源结合联合目标函数中的权重加在一起,构成一个多信息联合的复合伴随源,通过反传伴随源得到的伴随波场与正传波场做零延迟互相关即为(4)式的联合反演的梯度表达式.

