基于热力耦合的轴承失效分析
吴俊杰,朱振杰,孙德鹏,张进生,欧阳丛森,董配玉
(山东大学a.机械工程学院; b.山东省石材工程技术研究中心; c.高效洁净机械制造教育部重点实验室,济南 250061)
0 引言
机械设备作为现代机械制造行业的重要组成部分,备受行业关注,它直接影响着企业的工作效益和生产成本。随着科学技术的发展,滚动轴承在机械设备的支撑中得到了广泛地应用,行业对轴承使用寿命、工作性能等方面也提出了更高的要求[1-3]。部分机械装置和转运机具完成工作的关键结构之一是矩形导轨配合滚动轴承,它承载着设备的重量,同时也是转运工作的保证。滚动轴承在载荷作用下极易产生磨损、裂纹、疲劳破坏等故障,降低设备的工作性能,如果不能及时地发现,将造成严重的经济损失和安全问题[4-6]。
国内外学者针对轴承性能、轴承寿命、热条件下机床性能等方面进行了大量的研究。李苗苗等建立了热应力和结构应力共同作用下的角接触球轴承模型,对轴承寿命进行了分析和预测[7]。Josef M分析了热条件变化对机床性能的影响,要减小温度引起的热误差[8]。韩勤锴等建立了变载偏斜圆柱滚子轴承打滑非线性动力学模型,讨论了不同工况对滚子打滑速度的影响[9]。路遵友等提出了一种计入热弹性变形和粗糙度影响的有限长线接触热弹流润滑分析方法,分析了热弹性变形和粗糙度对圆柱滚子轴承润滑特性产生的影响[10]。结果表明高温会对轴承的变形量和应力场产生影响,导致零件使用寿命和工作性能的降低。
部分机械设备在选用滚动支撑时,因工作空间的限制,经常采用滚动轴承作为运动部件,但轴承因承载面应力集中、塑性变形等问题,经常出现失效现象。从静力学角度分析轴承符合设计标准,但轴承在滚动过程中因摩擦产生热量,热量得不到及时传递而在轴承内部积累,长时间工作后会产生局部高温。轴承内部温度过高产生的热应力与设备对轴承施压产生的应力叠加,共同作用下导致轴承失效,故热力学在校核的过程中不可被忽视。实际设计中多采用静力学校核忽略了热力学的问题。
本文建立了圆柱滚子轴承热力耦合的有限元分析模型,考虑了应力场和温度场的耦合作用对轴承性能的影响。通过分析获得了不同温度场下轴承的接触应力和等效应力,同时探究了稳定运行工况下的轴承工作参数。
1 轴承失效分析
机械设备的轴承在工作一段时间后,经常发生失效的现象,尤其在使用小轴承时,甚至发生轴承外圈断裂等情况,严重影响生产效率。为了合理选择轴承,避免轴承短时间内失效现象的发生,对裂纹的产生进行了探究。
在工程应用中,轴承的失效可以分为疲劳点蚀、塑性变形和磨损烧伤等三种形式。轴承外圈的断口如图1所示,断口平整,滚道面和滚动体表面没有鱼鳞状剥落或暗色梨皮状点蚀,表明轴承没有因为载荷过大而产生压痕,没有发生侵蚀或烧伤现象,可以初步确定是因为塑性变形的累积而造成的外圈断裂。

图1 断裂后的轴承外圈
对处于较低转速,尤其是承受较大径向载荷时,轴承的承载能力取决于塑性变形,应进行静强度分析。该机械设备的轴承共有12个,承载的总径向载荷为120 kN,故分布在每个轴承上的径向载荷为10 kN,属低速重载。在该工况下使用的轴承是NUP2215型圆柱滚子轴承,轴承的基本额定静态载荷最大可达208 kN,基本额定动态载荷最大可达150~186 kN,而作用在轴承上的载荷为10 kN,远未达到轴承的载荷极限,同时处于工作中的轴承,发热现象明显。由此我们推断该工况下,轴承外圈的断裂与热力耦合相关,所以基于热力耦合原理,针对轴承外圈的断裂现象,建立了有限元分析模型对轴承进行失效分析。
2 建立圆柱滚子轴承的有限元模型
2.1 建模及网格划分
有限元分析模型使用的圆柱滚子轴承型号为NUP2215,由于保持架和圆角对温度场分布的影响较小,为简化分析模型,在建模过程中忽略保持架和圆角,圆柱滚子轴承的几何模型如图2所示,轴承的结构参数见表1。将建立的模型导入Workbeach中,划分网格后共得到21 895个单元和8687个节点。
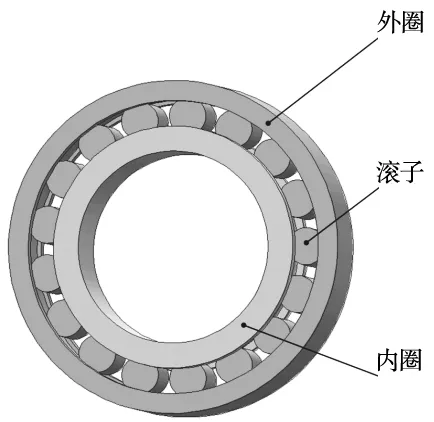
图2 圆柱滚子轴承模型示意图

表1 圆柱滚子轴承结构参数
2.2 确定材料参数
NUP2215轴承内圈、滚动体和外圈的材料均为GCr15轴承钢。在ANSYS Workbeach工程数据中新建GCr15材料,材料物理性质参数见表2[11]。

表2 GCr15轴承钢物理性质参数
2.3 设置接触特性
为模拟机械设备的实际运行工况,设置圆柱滚子轴承滚动体和内外圈的接触为摩擦接触,摩擦系数为0.03[11],法向刚度取软件默认为1,接触界面处理调整为接触。
2.4 定义边界条件
由于只对轴承在平衡状态下的温度场进行研究,故采用稳态热分析,在稳态热分析模块中定义了以下约束:
(1)为模拟轴承在运行过程中的发热量,对滚子与内外圈接触的表面上加载热流率,热流率为500 W。
(2)为模拟热量的传递,对轴承外圈加载热对流,对流换热系数为400 W·m-2/°C。
在静力学分析模块中定义了以下约束:
(1)为模拟轴承瞬时的运转状况和导轨对轴承的限制作用,约束轴承外圈外表面上所有节点xyz三个方向上的自由度。
(2)为模拟轴承运转,分别约束轴承内圈和外圈4个侧面上所有节点的轴向自由度。
(3)为模拟保持架对滚动体的限制作用,约束滚动体轴向的自由度。
(4)为模拟轴承内圈的转动,对轴承内圈添加旋转角度。
3 热力耦合仿真分析
3.1 数学模型
在温度场的影响下,轴承各个方向上的形变量极小,而微小的变形量对温度场的影响也极小,所以采用间接耦合方式,只研究单向的温度场-应力场耦合,即先进行温度场的分析,再将温度场结果导入应力场中进行耦合分析。在笛卡尔坐标系下稳态热分析的方程为:
(1)
式中,T为轴承的工作温度。
轴承在工作过程中,因摩擦产生大量的热,导致工作温度升高,产生较大的热应力,当热应力超过材料屈服极限时,轴承发生塑性变形。轴承应力增量dδ与应变增量dε关系可以表示为:
dδ=Dep·dε
(2)
式中,dδ为应变增量,dε为应变增量,Dep为弹塑性刚度矩阵。
3.2 有限元分析
为模拟轴承实际工况,对内圈施加方向为竖直向下,大小为10 000 N的力,仿真结果如图3、4所示。

(a)未考虑热力耦合效应 (b)工作温度为80 ℃

(c)工作温度为100 ℃ (d)工作温度为112 ℃

(e)工作温度为113 ℃ (f)工作温度为120 ℃ 图3 轴承接触应力图

(a)未考虑热力耦合效应 (b)工作温度为80 ℃

(c)工作温度为100 ℃ (d)工作温度为112 ℃

(e)工作温度为113 ℃ (f)工作温度为120 ℃ 图4 轴承外圈等效应力图
4 仿真结果及分析
4.1 数据分析
热力耦合仿真对比结果如图5、图6所示,机械设备在运行过程中,轴承的接触应力和等效应力随温度的升高而增大,且接触应力和等效应力的变化率随温度的升高而增加,温度越高,对轴承热应力的影响越大。
轴承的转速较慢,且承受的径向载荷较大,承载能力取决于轴承所允许的塑性变形,所以应进行静强度计算,同时机械设备在该工况下,轴承外圈的应力最大,当外圈满足设计要求时,整个轴承的工作性能也能够得到保证,故优先分析轴承的外圈。轴承钢的屈服强度为518.42 MPa,由分析结果可知,当温度达到113 ℃时,轴承的等效应力大于屈服强度,此时轴承外圈的强度将不满足设计要求,轴承会产生塑性变形,不能刚性回弹,导致轴承的工作性能降低,最终影响设备的加工质量和加工安全性,所以在该工况条件下,轴承的温度只有控制在112 ℃以下,才能保证工作效率。在实际的生产工作中,该机械设备的工况比较复杂,我们设置的工作温度应远低于失效温度,使轴承远小于材料的屈服强度,将轴承的失效可能性降到最低,这样才能在最大程度上保证设备安全稳定地运行。
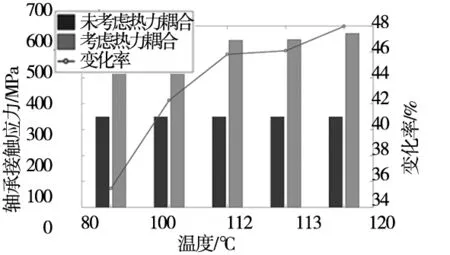
图5 温度场影响下的轴承接触应力结果对比
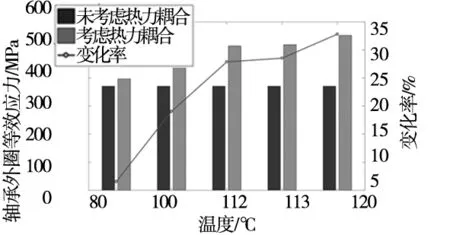
图6 温度场影响下的轴承外圈等效应力结果对比
4.2 结果分析
从图5、图6可以看出,考虑热力耦合后轴承的接触应力和等效应力均增大,且温度越高,轴承的接触应力和等效应力越大。由于轴承温度的升高,轴承润滑状态恶化,摩擦力增大,产生的热量不断累积,塑性变形增大,导致轴承的应力不断增大;同时在圆柱滚子轴承中,作用于滚动体与内外圈之间的载荷所形成的接触区域较小,所以滚动体与内外圈表面产生的应力通常都较大。因此,热力耦合作用下的应力过大是轴承外圈发生失效的主要原因,轴承设计选型时应该考虑热力耦合的影响。
5 结论
(1)仿真结果显示,圆柱滚子轴承的接触应力和等效应力随轴承工作温度的升高而增大。在使用轴承作为支撑部件的机械设备时,为避免轴承因热力耦合发生失效现象,可以通过周期性地停止设备工作,对轴承接触处进行降温,散发轴承因摩擦产生的热量,从而有效地延长轴承的服役期,提高设备的工作效率。
(2)长时间处于工作状态的轴承,特别是承受较大载荷时,设计选型时要综合考虑温度场对轴承性能的影响,在同等计算结论下,应该选择承载能力更高的滚轮轴承来改善工作状况。
(3)改善润滑条件和轴承的密封装置,可以防止混入粉尘等杂质造成润滑不良,从而减小工作过程中的摩擦力,降低轴承的工作温度,提高轴承的工作性能。

