GIS内壁检测的四足爬壁机器人运动学分析*
张 铁,吴骄任,蔡 蒂,吴凌峰
(1.华南理工大学机械与汽车工程学院,广州 510640;2.广州供电局有限公司,广州 510620)
0 引言
气体绝缘金属封闭开关(GIS)作为变电站的电气主设备之一,是电网安全、稳定运行的可靠基础保障。该设备由于采用了金属全封闭式结构,运行中不易对GIS的运行工况进行监测。当发生突发性内部故障,需要对内部故障或缺陷的表现形态和准确位置进行查找和判定。而传统的检修方式是检修人员采用有源式内窥镜检查气室内部各部件情况,判断设备的损坏状况,这种方式效率极低。本文针对变电站内部高压气体绝缘金属封闭开关内部检测,研究了一种小型的管道爬壁机器人。
国内外相关的专业学者对管道机器人进行了大量的研究[1],让机器人代替人工去作业。德国研制的多关节机器人MAKRO[2],每个关节由三个电机驱动。可实现在管道内的前进、转弯和越障,采用蠕动方式运动速度较慢。德国研制了MORITZ多足爬行管道机器人[3],有8足,每足有4个自由度,并且能够实现在管道中转弯,但是移动速度低,控制复杂。斯坦福大学研制了StickyBot[4]的仿壁虎机器人,形似一只壁虎,依靠脚掌的聚合物吸附性能吸附在垂直光滑的玻璃或者塑料表面以4 cm/s的速度爬行。
南京大学张千伟等[5]、浙江大学周坤[6]设计了一种四足机器人,用D-H进行正逆运动学分析,并分别设计了一种连续爬行步态和复杂地形路径规划方法。山东大学设计了一种基于五杆机构的四足机器人[7],每个足有3个自由度。分析了腿的正逆运动学,用MATLAB求解。并用ADAMS对步态规划进行了规划和验证。文献[8]设计出具有9个自由度的四足仿生机器人,使用NX软件对机器人进行小跑步态模拟,通过物理模型的运动效果验证了小跑步态的有效性。南京航天航空大学研制了仿壁虎四足爬壁机器人[9],建立运动学坐标系进行正逆运动学分析,用ADAMS对垂直壁面爬行进行了仿真。文献[10]设计了一种手足一体式四足步行机器人,对腿部建立运动坐标系,分析了其足端的可达空间和稳定性。上述机器人的运动学分析,不能准确地在基础坐标系下描述机器人的位姿,没有针对具体的轨迹规划分析其关节角度运动情况,没有对实际运动轨迹和理论轨迹进行分析,缺少实验论证。
本文设计了一种应用于GIS开关的四足管道爬壁机器人,通过建立了管道基础坐标系描述了机器人的位姿。基于机器人的运动学,为了避免足端和管道内壁发生碰撞,对足端进行轨迹规划,通过实验误差分析验证机器人运动学的可行性和准确性。
1 机械结构设计
机器人的运动空间是管道内部,要能够实现基本的运动步态,并且能够吸附在管道内壁上。所设计的四足机器人如图1所示,根据机器人的运动方向定义四足,分别为右前足(FR)、左前足(FL)、右后足(BR)、左后足(BL)四足,机器人各足均有3个旋转关节,通过微型直流伺服电机驱动实现机器人的抬腿、前进、后退或左右行走功能。如图1所示,机身腰部长2a、宽2b、高2c。其髋部连杆长度为L1,大腿连杆长度为L2,小腿连杆长度为L3,足端连杆长度为L4。足部末端安装真空吸盘,利用负压可以稳定吸附在管道内壁。摄像头安装在机器人腰部,实现管道内部情况监测,实时将视频数据传输出去。

图1 管道爬壁机器人机械结构
为了确定机器人在管道中所处的具体位姿,协调各个关节的运动角度从而实现机器人从某一位置移动到目标位置,避免运动过程中发生碰撞并保证运动稳定性和控制机身协调[11],故需建立机器人的运动坐标系并进行位姿分析和运动规划。
2 管道基础坐标系中机器人的位姿
2.1 机器人坐标系的建立
为了描述机器人的姿态和在管道中的位置,构建如图2所示的机器人坐标系。根据管道方向的不同,分别对水平管道和竖直管道进行分析,如图2a所示。
以管道的中心位置为原点,管道轴向为xO轴方向,以垂直向上为zO轴建立水平管道基础坐标系{O}。
以机器人机械中心为原点,xE轴与前进方向共线,垂直机身表面向上为zE轴建立机器人本体坐标系{E}。
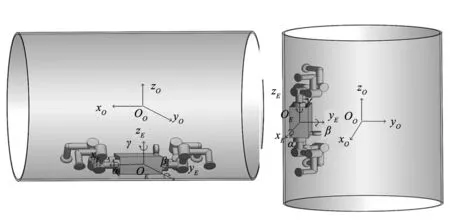
(a) 水平管道 (b) 竖直管道 图2 管道基础坐标系和机器人本体坐标系
建立竖直管道基础坐标系和对应的机器人本体坐标系,如图2b所示,以管道的中心位置为原点,管道轴向为zO轴方向,以水平方向为yO轴建立竖直管道基础坐标系{O}。
以机器人腰部中心为原点,以机器人向上运动方向为zE轴,垂直机身表面为yE轴建立机器人本体坐标系{E}。
机器人通过四足所搭配的真空吸盘吸附在壁面上,如图2a所示,机器人相对于管道内壁的位姿可由六个参数(LX,LY,LZ,α,β,γ)确定,机器人机身坐标系原点OE在管道世界坐标系{O}中的位置(LX,LY,LZ),其中LX表示机器人在管道中前行的位置,LY与LZ的平方和的开方表示机器人距离管道中心的长度。机器人机身坐标系相对管道基础坐标系沿x轴,y轴,z轴旋转的角度为 (α,β,γ)。
根据坐标系平移和旋转变化的规律可得坐标系{E}相对{O}坐标系变换矩阵为:
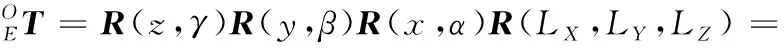
(1)
基于机器人机身坐标系和管道基础坐标系的关系,通过式(1)描述机器人的位置和姿态。本文对机器人姿态的分析仅针对图2a的水平管道,竖直管道的分析方法与此相似本文不再陈述。
2.2 机器人爬行起始位姿确立
不同的姿态对应着不同的位姿态参数,机器人的运动要适应不同的管径变化,结合管道内壁爬行的特点,选择固定的机器人爬行起始姿态,如图3所示。足部髋关节角度不为0,足端连杆垂直于内壁,将此时的机器人姿态称为运动起始姿态。此姿态下机身本体坐标系原点OE置于管道基础坐标系原点OO的正下方,LY=LZ=0。偏角α=β=γ=0。

图3 起始状态下的机器人坐标系
由图3,可得几何关系:
(2)
(3)
联立式(1)~式(3)可得起始状态下管道基础坐标系{O}与机身坐标系{E}之间的关系:
(4)
同理可得BR足端在管道基础坐标系下的位置为:(a+L1+L3,Rcosθ0,-Rcosθ0)。
当确定了机器人在管道基础坐标系中的起始位姿,需分析求解各个关节的正运动学解和逆运动学解。
3 机器人关节运动学分析
3.1 机器人单腿运动学分析
对机器人建立坐标系进行运动学分析,如图4所示,根据转动关节的位置,建立BR单足坐标系。机身坐标系{A0}与机器人本体坐标系{E}重合。坐标系{A1}建立在髋部微型直流伺服电机轴心上,三轴方向与坐标系{A0}相同。坐标系{A2}建立在大腿微型直流伺服电机轴心上,其xA2轴与髋部连杆共线。坐标系{A3}建立在小腿微型直流伺服电机轴心上,xA3轴与髋部连杆平行。坐标系{A4}建立在小腿末端上,xA4轴与小腿连接杆平行。坐标系{A5}建立在足端上,三轴的方向与坐标系{A4}相同。
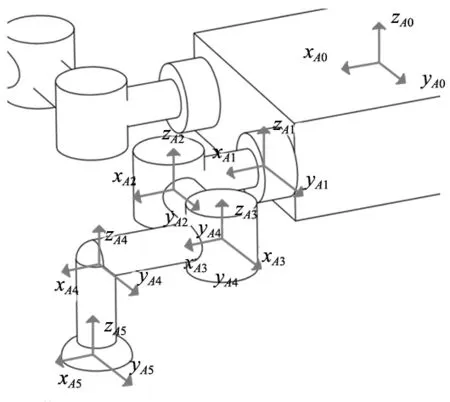
图4 单BR足坐标系
即坐标系{A0}相对于坐标系{A5}的旋转矩阵为:
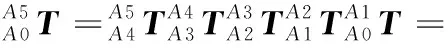
(5)
式中,θA1,θA2,θA3分别表示BR足髋部微型直流伺服电机、大腿微型直流伺服电机、小腿微型直流伺服电机的转角。
根据式(5),可得BR足的足端在机身坐标系下的坐标与关节转角的关系为:
(6)

(7)
通过式(7)的正运动学分析,得出关节角度与足端位置的关系。机器人的运动控制中,只需要读取关节角度值,就可用以上运动学解求出机器人足端的位置。
在运动控制中,先给定足端的目标位置,根据目标去控制关节旋转的角度,要进行逆运动学分析。对式(6)、式(7)进行逆运动学求解可得:
(8)

3.2 机器人四足运动学逆解
参照图4机器人单BR足坐标系建立和逆运动学求解,求解四足足端位置在机器人坐标系的位置。如图5所示,(xE1,yE1,zE1),(xE2,yE2,zE2),(xE3,yE3,zE3),(xE4,yE4,zE4)分别表示BR,BL,FR,FL四足的足端在机器人机身坐标系{E}下的坐标位置。
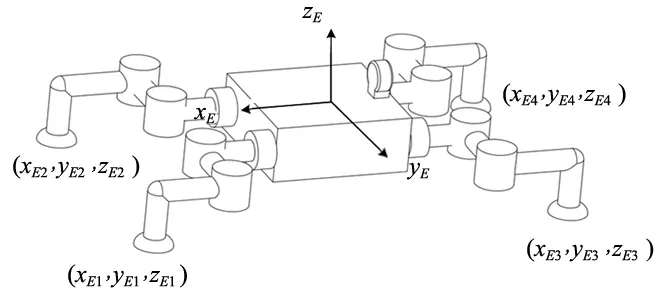
图5 机身坐标系
参考式(7)、式(8)的求解过程,可得四足的足端在机身坐标系{E}下的运动学逆解:
所以,山东省政府应在金融、财政等方面制定创新制度,着力支持设计、研发、营销、培育品牌等对结构升级优化有重大影响的核心环节,积极推动制造业企业的自主创新。通过持续推进科研经费管理改革和科技成果奖励评价,着重激励、引导创新要素汇聚于企业,加速构建围绕企业、政府、高校、科研单位等技术的创新体系,促使科技研发、经济市场更好地融合和科研成果更好更快地被转化,进而实现科研成果的产业化。
(9)
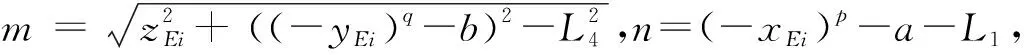

表1 p和q的取值
由式(9)可得对于机器人任意姿态的关节角度,只要给定任意的足端目标位置,机器人都可以通过机器人运动控制系统指令控制各个关节准确到达指定位置。
4 机器人运动轨迹规划和仿真
4.1 机器人直线运动轨迹
给定足端的目标位置,对应的关节角度可以求解得出,但是对于关节的运动过程,还需要对运动路径进行规划,得出对应的连续关节角度变化。
足端空间直线路径是运动轨迹中最基础的[12],用来简单的测试机器人足端是否能够按照预先规划的目标运动。并且复杂的曲线路径也可以认为是多段极短的直线路径组合而成。
如图6所示,足端运动规划为直线路径,在机身坐标系下的路径方程为:
(10)
式中,0≤s≤hx;hx表示运动步长。
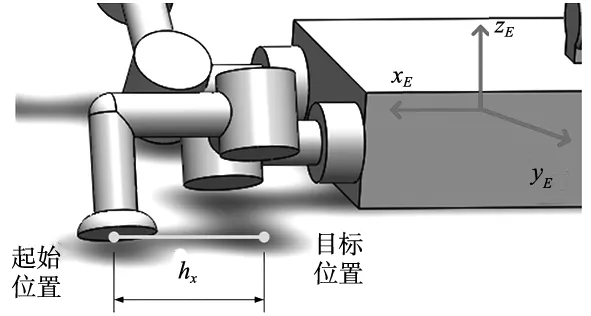
图6 空间直线路径
将路径方程带入式(9)中,在MATLAB中仿真求解可得如图7所示的关节角度曲线。

图7 直线路径关节角度曲线
如图7所示,机器人足端进行直线轨迹运动时,髋关节角度不变,一直为0,足端向前运动时,大腿关节逆时针旋转,角度变大,小腿关节顺时针转动,角度变小。
通过仿真可得机器人足端直线运动对应的关节角度变化,按照该规律对机器人关节控制就能使机器人足端按照预先设定好的空间直线轨迹运动到达指定目标。
4.2 机器人曲线运动路径
机器人在管道内运动的过程中,需考虑足端与壁面的碰撞和速度方向[13]。抬足和落足时要保证速度与壁面的夹角较大,以提高运行的稳定性,因此需要更为复杂的曲线轨迹来满足运动控制的需求[14],正弦路径更精确稳定,运动平稳,其轨迹规划如图8所示。
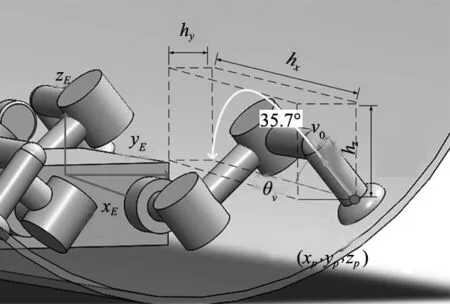
图8 管道曲线路径
该路径的在机器人本体坐标系下的表达式为:
(11)
式中,0≤s≤hx;hy,hz表示y和z方向的抬腿高度。
在该正弦路径运动中,为保证抬足和落足的速度与壁面有较大的夹角,应满足:
(12)
因此,其初始速度方向与内壁夹角为:
(13)
将曲线路径在MATLAB中仿真求解可得如图9所示的关节角度曲线。

图9 曲线路径关节角度曲线
如图9所示,机器人足端进行曲线轨迹运动时,髋关节角度先增大后减小,曲线运动时足端在前进方向也有位移,大腿关节角度变大,小腿关节角度变小。
5 机器人轨迹运动实验
如图10所示为四足机器人本体,机器人共有12个直流伺服电机。腰部中间放置STM32控制板用来接收遥控指令和控制直流伺服电机的运动。真空控制系统管路由外部引入。

图10 四足机器人本体
如图11所示进行机器人运动轨迹测试,图11a是机器人足端的空间直线路径,图11b是机器人位于GIS管道开关中足端正弦路径,在实验中机器人足端都可以按照预定轨迹路线运动。

(a) 空间直线路径

(b)管道正弦路径图11 路径规划实验
在路径规划实验中,通过伺服电机自带的角度传感器测量关节的角度,计算得出机器人足端运动的实际轨迹,与理论轨迹进行对比,其轨迹对比如图12所示。

(a) 空间直线路径 (b)管道正弦路径图12 理论轨迹和实验轨迹对比
如图12所示,在z轴方向上,实际的直线轨迹和曲线轨迹对理想轨迹都有较小的负偏移量。原因是足端质量较大,受重力作用产生偏移。在未来的工作中,可以对运动进行补偿以减小误差。

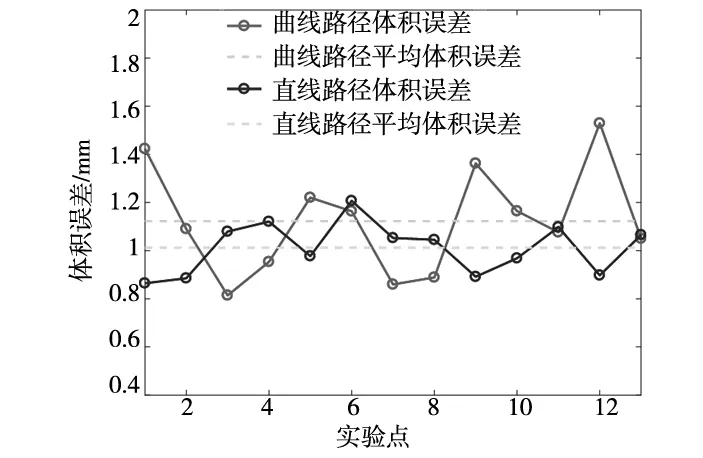
图13 体积误差分析
机器人足端运动时,直线路径平均体积误差为1.03 mm,标准差为0.3 mm,曲线路径平均体积误差为1.14 mm,标准差为0.25 mm。整体上运动路径的体积误差较小,满足机器人的运动,运动学模型精度较高。
6 结论
(1)设计一种GIS内壁检测的四足爬壁机器人,经运动学分析和实验验证,它能够满足在管道内全方位爬壁的要求,其结构设计合理。
(2)通过对目标位置分别进行直线路径和曲线路径规划,避免了在运动过程中足端与壁面的碰撞,实现了足端平滑运动。
(3)理想轨迹和实际轨迹的平均体积误差为1.09 mm,误差较小,运动学模型精度较高。

