连续体结构拓扑优化敏度过滤研究*
张国锋,徐 雷,李大双,余方超
(四川大学机械工程学院,成都 610065)
0 引言
连续体结构拓扑优化[1]已成为当前拓扑优化研究方向的热点问题之一,其在诸多领域具有普遍应用。变密度法[2]作为常用的拓扑优化方法之一,因其设计变量少、程序简单及应用范围广等特点被广泛应用,其实质是单元密度为0~1的离散变量之间的排列组合的问题。因进行有限元计算分析,导致在整个的优化过程中产生如棋盘格现象、网格依赖性等数值不稳定的问题[3],使其直接制造性不强,制约了变密度法在结构拓扑优化领域的发展。
国内外学者针对上述问题进行了广泛和深入的研究,Sigmund O等[4]提出半径过滤方法,有效消除棋盘格问题,但优化结果常出现边界扩散现象。Haber R B等[5]提出周长控制法,需要人为反复调试参数,且对局部棋盘格现象抑制效果不明显。Petersson J等[6]提出局部密度斜率控制法,由于引入额外的约束条件,导致运算耗时,求解难度大。朱剑峰等[7]提出一种通过影响因子控制敏度修正程度的方法,尽管对迭代速率,结构刚度均有提升,但仍出现一定的边界扩散现象。陈垂福等[8]通过对中心及周边元素采用不同权重来抑制棋盘格现象,但并不能有效控制最小尺寸。杜义贤等[9]借鉴粒子群优化算法中粒子状态的更新方法来抑制棋盘格现象,但在优化过程中可能出现细小孔洞的情况。龙凯等[10]提出一种考虑密度梯度的方法,但可能出现结构孔洞数量发生变化,影响最后的优化结果。
本文在现有研究的基础上提出了一种改进的敏度过滤方法,该方法通过引入新的卷积因子,结合原有卷积因子建立三者在一定权重比分配下的数值关系,并采用一种带有预设修正权值的方法,来弱化边界扩散的问题。该方法在有效消除棋盘格等问题的同时,有效提升迭代速度,降低柔度收敛值,提升结构刚度。以柔度最小化为优化目标,通过选取多个二维平面结构算例验证了本文方法的可行性。
1 变密度法拓扑优化理论及数学建模
固体各向同性材料的惩罚法[2](Solid Isotropic Microstructures with Penalization,SIMP)即变密度法是将设计域离散成一个由X轴及Y轴上的元素集合定义的有限元单元,选择材料密度作为结构拓扑优化的设计变量,根据最优性准则或数学规划方法,在参考域内重新分配材料,得到最优结构拓扑。在大多数情况下,优化目标是在给定的载荷模式和边界条件下获得结构的最小重量。
假设选用各向同性材料作为研究对象,材料的泊松比取值是一个与材料密度等其他参数无关的常量,建立相对密度与弹性模量的函数关系为:
(1)
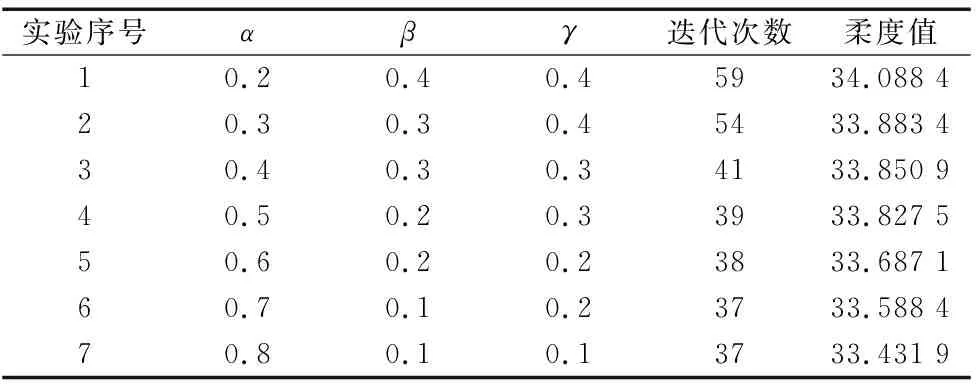
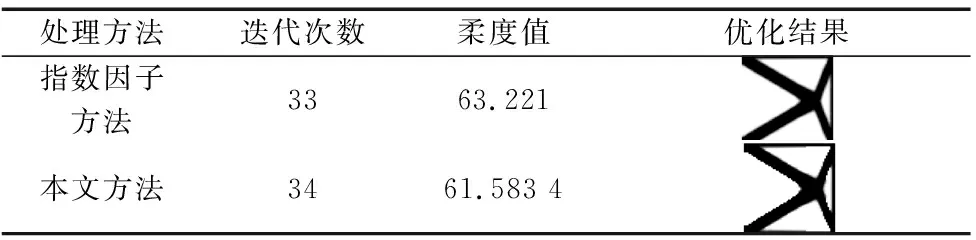
式中,ρi为第i个元素相对密度值,p为惩罚因子,E(ρi)为第i个元素的弹性模量,Emin表示孔洞部分中元素的弹性模量,E0为实体部分中元素的弹性模量。为了保证数值计算的稳定性,通常取Emin=E0/1000,并且0 当ρi=1时,单元为实体结构,当ρi=0时,单元为空洞结构。通过控制惩罚因子p的值,实现元素密度向[0, 1]两端快速收敛,从而得到接近理想状态且材料最优分布的离散结构,从而得到最优的材料分布。 变密度法假定每个单元的刚度矩阵依赖于惩罚因子p相对密度的改变,建立材料相对密度与材料弹性模量间显示非线性的函数关系,如图1所示。 图1 变密度法密度插值函数模型 随着惩罚因子p的增加,结构刚度逐渐受到惩罚,对给定体积的材料,其中间密度值向两端收敛,在单元网格的约束下拓扑优化单元将重新分布,惩罚因子p一般是通过连续法从下界递增到上界,每一步收敛后p递增,以避免过早收敛到局部最小值。 在给定的体积约束条件下,选取最小柔度作为目标函数。基于变密度法优化问题可表述为: find:ρ={ρ1,ρ2,···,ρn}T∈R (2) (3) subject to: (4) 式中,C(ρ)为给定拓扑的柔度,U是全局位移矢量,F是全局负载矢量,K是结构全局刚度矩阵,N为元素个数,k0是单位杨氏模量的初始元素刚度矩阵,V(ρ)是优化后结构体积,V0是设计域的C初始体积,f是预先设定的体积分数,ρmin是一个包含最低允许相对密度的向量。 优化准则法[11](Optimality Criteria,OC)在求解过程中具有收敛迅速,求解方式简单,容易实现等特点。对于一定体积比约束下的柔度最小化问题,宜采用OC算法。OC算法的主要实现方式是利用目标函数与约束条件建立拉格朗日方程,将约束问题的约束与目标函数结合,成为无约束问题。通过对拉格朗日函数分析计算,可确定设计变量的优化迭代准则可表示为: (5) 式中,λ为当柔度取极值时全设计域中元素的应变能密度。 目前在变密度法拓扑优化中普遍存在着棋盘格、网格依赖性现象。棋盘格现象,就是在不对敏度信息进行处理,使得拓扑优化结果呈现单元之间的单点连接,形成单元密度为0、1交替排布的情形,导致不具备制造性,这种现象的存在是采用有限元求解无法克服的。网格依赖性和网格划分大小具有密不可分的关系,不同的划分结果对优化结果产生较大影响,网格划分越大,拓扑优化结果越容易出现细长杆等微小结构,导致优化结果不具备良好的可制造性。 敏度过滤能够有效解决数值不稳定的问题,结构的灵敏度分析在进行拓扑优化时非常重要的,对模型的收敛判断具有决定性的作用。结构敏度可表示为: (6) 目前常用的敏度过滤技术是Sigmund提出的敏度过滤方法,是一种局部约束方法,其本质是通过人为设定一过滤半径,在此范围内通过引入线性卷子因子将中心单元与其余单元之间的距离进行加权平均计算,修正目标函数的灵敏度,进而构建这一范围内所有元素的敏度均值,更新敏度后续的迭代处理,从而解决棋盘格问题。Sigmund敏度过滤方法可表示为: (7) 式中,Hei为卷积因子,rmin为最小过滤半径,Δ(e,i)为元素i到单元元素的中心距离,由于设计变量的取值为[0, 1],取ρmin=10-3,防止造成计算上的奇异性。 Sigmund敏度过滤方法存在如下问题:当所设定的过滤半径较大时,拓扑优化边界会出现过度磨平的情况,这也导致优化结果很容易出现边界扩散等问题。 为解决传统Sigmund敏度过滤方法中容易出现边界扩散现象的问题,采用一种改进的敏度过滤方法,该方法在保留原有卷积因子的条件下,引入两种非线性卷积因子Hin及Hat,其公式表示为: (8) (9) 式中,rmin及Δ(e,i)与Sigmund敏度过滤方法中卷积因子定义一致,λ为模型预先设定的网格最大数,即λ=max{x,y}。 由于Hin、Hat二者均为非线性卷积因子,能够在根本上保证中心单元的敏度权值不会因过滤半径的改变而改变,二者均为二阶非线性函数,可以有效扩展卷积的拟合区域,使得在过滤半径领域内中心单元的权重值远大于其余单元的权重值,确保中心单元敏度在迭代过程中不被过多的平均处理,保证最终拓扑优化结果尽可能避免过度磨平的情况出现。 (10) 式中,α、β及γ分别为卷积因子Hi、Hin及Hat的修正权值,满足α+β+γ=1,其控制各卷积因子对目标函数敏度值的影响程度。 采用一种带有预设修正权值的方法,弱化边界扩散的问题,可表示为: (11) 式中,预设修正权值k=10-3,经数值计算验证取阈值η=0.7为宜,|ρi-ρe|为两离散单元密度差值。 通过该方法的处理,能够使拓扑优化时具有黑白较为分明结果,与此同时在结构内部保证良好的均匀效果。 综上可得改进的敏度过滤方法可表示为: (12) 2.3 敏度过滤方法参数分析 为研究修正权值对拓扑优化结果的影响,采用算例1所示的二维应力结构拓扑优化确定本文方法的参数,为更准确地确定本文方法的参数,设定迭代终止准则的设计变量变化率ε=0.01,数值实验结果见表1所示。 表1 不同参数计算结果 由表1数据可知,实验1与实验2所得结果显示迭代次数较多,且柔度值较大;实验6与实验7所得结果显示迭代次数较少,且柔度值较小,但是拓扑优化结果容易出现微小孔洞。所以当α、β及γ满足α=0.4~0.6、β=0.2~0.3、γ=0.2~0.3且满足式α+β+γ=1时,该方法具有较好的算法合理性和迭代效率。 该方法可以有效控制棋盘格现象,解决边界扩散问题,获得边界清晰的优化结果,并大幅度提高了优化速度,有效提升结构刚度。 采用多个拓扑优化典型算例来验证本改进的敏度过滤方法(以下简称本文方法)在不同条件下的有效性及可行性。算例通过MTLAB-2016a编程实现。在算例运行计算中,采用平面四结点双线性正四边形单元离散结构,实体材料的弹性模量E=1,泊松比ν=1,选用最小过滤半径rmin=1.5,设定迭代终止准则的设计变量变化率ε=0.01。 算例1:如图2所示二维平面应力结构,该结构设计区域为60 mm×40 mm,网格划分为60×40,结构左端采用全平面固定约束,结构右端中间节点处受到载荷F=1的竖直向下载荷作用。 图2 算例一模型示意图 通过对比无敏度过滤方法、Sigmund敏度过滤方法、反三角函数因子方法[7]及指数因子方法[7]拓扑优化结果,分析及验证本文方法是否具有可行性,采用体积比为0.5的约束条件,惩罚因子p=3,得到多种处理方法下的拓扑优化结果如表2所示。 表2 算例1不同处理方法拓扑优化结果 分析表2优化结果,无敏度过滤方法拓扑优化结果呈现出复杂的棋盘格现象,采用后4种方法均能很好地抑制棋盘格的产生,结构拓扑图形清晰。Sigmund敏度过滤方法、反三角函数因子方法及指数因子方法均出现灰度单元的现象,采用本文方法得到的拓扑优化结果在一定程度上避免了边界存在灰度单元的现象。在相同的预设条件下,反三角函数因子方法、指数因子方法及本文方法在拓扑优化时的迭代次数均在40左右,而采用本文方法时,优化结构具有最小的柔度值和良好的优化效果。 算例2:如图3所示经典Michell结构,该结构设计区域为80 mm×40 mm,左下角节点处采用固定约束,右下角节点处采用铰链约束,在图示结构底部中间节点处受到载荷F=1的竖直向下载荷作用。 图3 算例二模型示意图 分别对算例2采用Sigmund 敏度过滤方法、反三角函数因子方法、指数因子方法及本文方法,通过选用不同参数,分析及验证后处理方法在不同网格计算密度、不同惩罚因子时是否具有可行性,采用体积比为0.5的约束条件,优化结果如表3所示。 表3 不同优化方法拓扑优化结果 分析表3优化结果,本文方法能够很好地抑制数值不稳定现象,在不同网格划分、惩罚因子的条件下,本文方法均具有良好的表现,对比其他三种方法,本文方法在拓扑优化时具有较少的迭代次数,与此同时优化结构的柔度收敛值最小,在一定程度上,避免了边界存在中间单元的现象,有效验证了本文方法的可行性。 图4 算例三模型示意图 算例3:如图4所示二维平面应力结构,该结构设计区域为60 mm×60 mm,网格划分为60×60,结构左端采用全平面固定约束,在图示结构右上角受到载荷F=1的竖直向上载荷作用,右下角受到载荷F=1的竖直向下载荷作用。 通过对比Sigmund敏度过滤方法、反三角函数因子方法及指数因子方法拓扑优化结果,分析及验证本文方法在多重载荷情况下是否具有可行性,采用体积比为0.4的约束条件,惩罚因子p=3,优化结果如表4所示。 表4 算例3不同处理方法拓扑优化结果 续表 分析表4优化结果,本文方法在多重载荷情况下同样能够很好地抑制数值不稳定现象,对比其他三种方法,本文方法在拓扑优化时迭代次数稳定,且优化结构的柔度收敛值最小,有效验证了本文方法的在多负载工况下的可行性。 变密度法作为处理拓扑优化问题的主流方法之一,具有设计变量少、效率高等优点。但传统的变密度法在优化过程中常出现如棋盘格现象等数值不稳定现象,使得优化模型提取较为困难,不具备良好的可制造性。本文在现有研究的基础上,提出了一种改进的敏度过滤方法,实验结果表明,该方法能有效消除棋盘格等问题,且有效提升迭代速度,降低柔度收敛值,提升结构刚度。但是,本文方法在拓扑优化结果的离散度方面还需进一步改进,这也是今后研究工作的主要方向。
2 敏度过滤方法
2.1 Sigmund敏度过滤方法
2.2 一种改进的敏度过滤方法


3 实验分析验证






4 结论

