基于ADAMS的AGV台车回转机构动力学分析*
周小容,李永聪,袁 森,陈海虹
(1.贵州大学机械工程学院,贵阳 550025;2.贵州理工学院机械工程学院,贵阳 550003)
0 引言
某AGV台车的上盘与下盘之间进行回转的传动机构为三级齿轮减速器,在回转过程中发现存在明显抖动和停止不及时的问题。
传动间隙和重合度是影响传动系统平稳性和传动精度的主要关注指标。国内外学者对其进行了较为深入广泛的研究,竹振旭等[1]对减速器传动误差影响因素进行了敏感性分析,结果表明下级间隙较相对上级对传动特性的影响更为明显,且随着级数增加存在累积效应;卢琦等[2]利用ADAMS软件对减速器进行了动力学仿真,认为传动间隙对传动精度存在较大影响,且传动比越大间隙造成的影响越明显;张慧博等[3-4]提出了齿侧间隙与轴承间隙的耦合作用方程,利用Newmark法进行了数值仿真,得到了不同间隙组合对传动精度和稳定性的影响。结合以上研究可知,减小传动比和传动级数可有效减小传动间隙,提高传动精度。Podzharov E[5]对重合度进行了研究,结果表明提高重合度可有效改善平顺性,并提出了增加啮合齿数和修改变位系数的改进方法。当一侧齿轮齿数增加到无穷大时,即演化为齿轮齿条传动,此时重合度达到最大。冯定等[6]提出了不同形式下齿轮齿条重合度的计算公式,并给出了长齿条的布置方法。顾寄南等[7]以重合度为优化目标建立了数学模型,确定了最优传动方案,并用仿真方法进行了对比验证。张祖芳等[8]利用龙格库塔法对考虑传动间隙的齿轮模型进行了数值仿真求解,讨论了重合度对齿轮副动态特性的影响。
为解决平顺性差和响应不及时的问题,本文从理论上分析了多间隙的耦合关系,同时考虑到提高重合度,提出了新的传动方案。利用ADAMS软件对两种方案进行了动力学仿真对比,为样机改进提供了理论支撑和指导意见。
1 理论分析
图1为某AGV台车回转部分的传动系统,小齿轮1由液压马达驱动,在通电状态下液压管路有保压能力,运转到位停止后可保证该马达直驱的齿轮1不会被动转动。经3级减速后,动力被传递到末端大齿圈(齿轮5)。由于该台车有升降功能,故齿轮5设计为大齿厚形式,即齿轮5相对于齿轮4在轴向上可以实现升降滑动。相关参数详见表1。

(a) 传动系统实物图

(b) 传动系统结构示意图图1 台车上盘回转传动系统
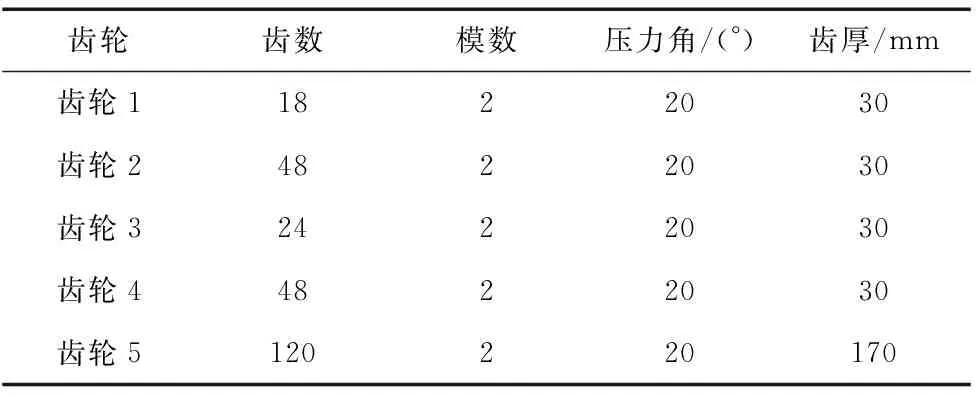
表1 各齿轮参数

图2 齿轮多间隙耦合模型
液压马达可保证齿轮1平稳输出和迅速停止,但由于传动过程中传动间隙等因素累加后,从实际情况来看,齿轮5的动态特性表现较差。图2为单对齿轮副的多间隙耦合模型,包括主动齿轮A和从动齿轮B两部分。传动间隙包括各自轴承处的径向间隙Δa和啮合处的齿侧间隙Δb两部分,齿轮中心距随两种间隙的变化而变化。由图中可知,在运转过程中从动轮由于回转中心O2偏离轴承中心,使得轴承处出现径向间隙Δa。此时中心距O1O2将发生变化,进而影响到齿侧间隙Δb的大小。考虑齿轮转子系统中径向间隙与动态齿侧间隙的耦合关系,故单对齿轮动力学方程可表示为:

(1)
其中,齿侧啮合力Fb和轴承处径向接触力Fc可用模型表示为:
(2)
(3)
式中,f(b)为啮合线方向位移,Cb为轮齿间的阻尼系数,Kb为轮齿之间的接触刚度;δ为轴承处的嵌入量,Cc为轴承处的阻尼系数,n为力指数,取决于材料属性,查阅文献[9]后取1.5,Kc为轴承处的接触刚度。
另外,由于中心距A的变化,齿轮啮合线N1N2及啮合角α′等参数几何关系变化如图3所示。

图3 齿轮含间隙啮合示意图
由图3中可以看出,当中心距扩大后,会导致啮合角α′的增加。根据重合度计算公式:
(4)
式中,z1、z2分别为主动轮、从动轮齿数,αa1、αa2分别为主动轮、从动轮齿顶压力角,α′为啮合角。由式(4)可知,在啮合过程中,重合度与齿数、齿顶压力角(一般为定值)和啮合角有关,所以为提高重合度应考虑增加齿数或减小啮合角。而齿轮分度圆直径为齿数与模数的乘积,考虑到齿轮承载能力,所以模数不宜过小;同时要考虑空间尺寸,所以齿数也不宜过多。另一方面,由于齿侧间隙不可避免地会增大啮合角,且随着减速级数增多存在累积效应。因此,本文提出了以齿轮齿条(下称方案2)代替三级外齿轮减速器(下称方案1)的传动机构,重合度最高可达1.981,远高于齿轮传动1.3~1.4的许用重合度。方案2一方面可以增大齿数(齿条可看作齿数无限大的外齿轮),另一方面减少了齿轮传递的级数,大大降低由间隙、变形等造成的综合误差。驱动源由高速的液压马达改为低速的液压缸,可以保证较大的动力输出和较高的传动精度。
2 动力学建模与仿真
根据如图4所示现有实物,建立如图5所示的台车三维模型,在模型内可以对2种方案进行对比。在保证布置空间和上盘旋转角度的前提下,确定齿条齿数为80,齿厚为20 mm。

图4 台车整体实物图
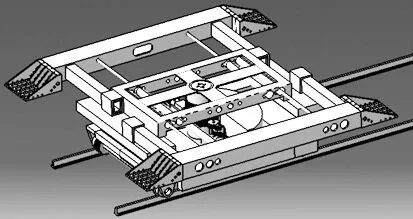
图5 台车整体三维模型
为减小计算量,只对传动部分进行动力学仿真,经转换格式并在ADAMS中进行相关约束后,两种方案的虚拟样机模型如图6、图7所示。
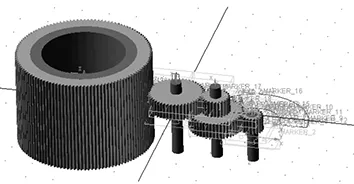
图6 方案1虚拟样机模型

图7 方案2虚拟样机模型
主要设置为:方案1中,将齿轮1与齿轮轴通过转动副连接,并设置转速驱动;其余所有齿轮之间均不采用齿轮副连接,而通过力接触命令实现力的传递,这样可以较为真实地计算出每次碰撞的过程;同样齿轮2~5与各自齿轮轴之间通过力接触命令连接,而不采用旋转副连接;减速器在重力方向不作讨论,所以取消重力选项并通过平面约束命令限制其轴向的跳动;所有轴与大地固连,齿轮2与齿轮3固连。方案2中,齿条与大地间通过水平移动副连接,并设置滑动驱动;齿条与齿轮之间设置力接触,其余与方案1相同。在进行动力学仿真时,应考虑材料属性和摩擦等因素,参照相关文献[10]进行了定义,详见表2。经仿真验证,两个模型均满足仿真要求。
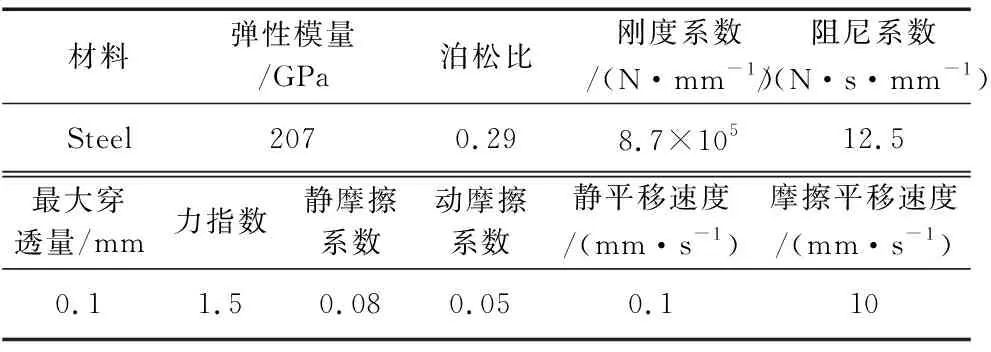
表2 虚拟样机模型参数
3 仿真结果对比分析
考虑到实际应用对回转过程中的平顺性、响应速度和传动精度有较高要求,分别以输出齿轮的转速、径向位移和齿侧啮合力3项为指标进行了对比。
3.1 输出齿轮转速
根据实际需求,欲保证齿轮5最快输出转速为30 deg/s,根据表1计算传动比,方案1输入转速为400 deg/s,方案2输入速度为20π mm/s。分别对两种方案进行仿真试验,为考虑实际工作时的变速问题,设置了两组STEP函数驱动:STEP(time,0,0,1,7)+STEP(time,4,0,5,-7)和STEP(time,0,0,1,20×pi)+STEP(time,4,0,5,-20×pi)以实现在0~1 s内由0 deg/s逐渐加速到30 deg/s,保持3 s后在第4~5 s内减速至0 deg/s。结果如图8、图9所示。
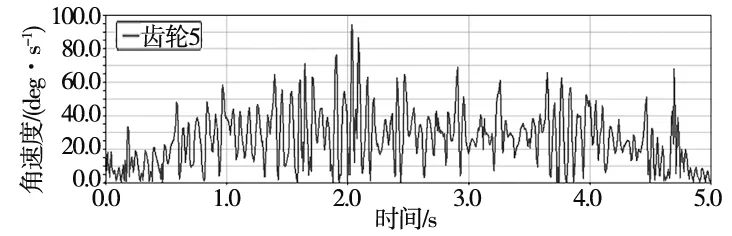
图8 方案1输出齿轮角速度变化率

图9 方案2输出齿轮角速度变化率
由图8可以直观看到方案1转速波动较为杂乱,且幅值较大,根据后处理界面显示的数据来看,虽然整个过程(含加减速过程)的均方根值为29.5 deg/s,较为接近目标转速,但1~4 s内瞬时转速在0~94.5 deg/s之间,存在过多不稳定的瞬时抖动,对载物和台车均有不良影响,应尽量避免。而图9中方案2由于只有一级传动,所以在加减速和恒速过程中均表现平稳,其中1~4 s内瞬时转速区间缩小至23.2~43.6 deg/s,波动幅度降低了78.4%,不良抖动明显减少,从动态响应来看明显优于方案1。
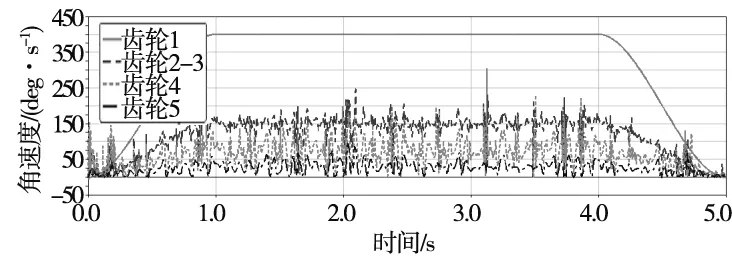
图10 方案1各级齿轮角速度变化率

图11 方案2齿轮转速、齿条速度变化率
为探究转速波动来源,分别将2种方案中所有齿轮的转速(速度)进行纵向对比。首先从图10可以发现方案1中转速波动从齿轮2即开始出现,但齿轮2转速相对较高,波动幅度相对自身转速较小,尚可看作较为稳定的输出。但随着级数增加,间隙累积导致了波动幅度的增加,结合图11对比发现,减少减速级数可以有效降低由间隙累积造成的转速波动。同时自身转速的降低,进一步提高了波动幅度与自身转速的比值,造成了输出齿轮的不稳定现象。以上结果表明该方案不宜应用在多级传动和低转速工况。
3.2 输出齿轮径向位移
分别对2种方案中输出齿轮的径向位移进行讨论,为对比输出齿轮分度圆切线方向上的振动,如图12、图13所示分别提取了方案1中齿轮5的Y方向和方案2中齿轮5的X方向位移(两组的空间位置存在差异)。
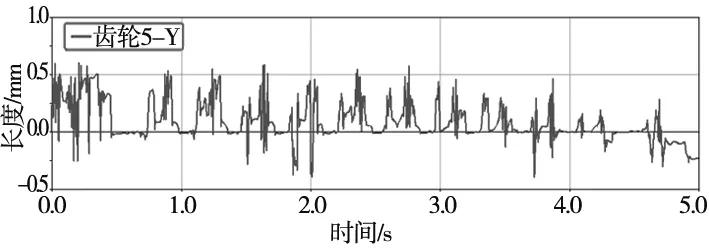
图12 方案1输出齿轮径向位移

图13 方案2输出齿轮径向位移
由图12和图13可以看出,方案1的径向振幅远大于方案2,且在加减速阶段没有明显的过渡。经结合3.1小节分析可知,齿轮4亦为非平稳运转,其复杂多变的跳动造成了传递至齿轮5的驱动力为非平稳力,处于大小冲击交替状态。而图13中,驱动力来自于平稳输出的齿条,在传递过程中变形量较小,X向振幅在±0.007 mm内近似正弦交替变化。同时由于没有多级减速吸收,输出齿轮在加减速阶段有较为明显的过渡变化,避免了受力突变,平顺性和传动精度均有较大的改善。
3.3 输出齿轮齿侧啮合力
分别提取与3.2小节相同方向的齿轮5与上级齿轮之间的齿侧啮合力,如图15所示对2种方案进行了对比和分析。

图14 方案1齿侧啮合力

图15 方案2齿侧啮合力
对比图14、图15可以发现,两种方案下的齿侧啮合力均在±3500 N之间,但方案2的波形更为平顺,不规则跳动较少,且在起步和结束阶段均有一定过渡。经分析可知,平均啮合力主要取决于负载和转速,而两种方案的工况基本相同,所以啮合力幅值相差不大。齿条直驱的方式减少了中间环节,引入的干扰因素较少,而方案1中齿轮2~齿轮4在传递过程中的相互作用会影响齿轮5的啮合,所以存在诸多小幅跳动。图15中,在起始阶段存在由静摩擦向动摩擦转变的过程,所以启动瞬间受力最大,而后迅速降低;另外在加速和减速阶段均存在一定过渡期,其主要原因是驱动速度此时为线性变化。啮合力为正负交替状态是因为齿轮5处于受力加速-受摩擦减速-受力加速的循环状态中,在受摩擦减速时处于齿背啮合状态,故齿侧啮合力为负值。另外,齿轮齿条传动的重合度要高于齿轮减速器传动,在平均啮合力接近时,齿轮齿条所受压强较小,有助于提高传动机构的使用寿命。
4 结论
通过对两种方案进行动力学仿真对比,结果表明原方案确实存在不合理之处,新方案的动力学响应特性明显优于原方案,为实际工程样机的改进提供了指导意见。
(1)方案2的输出转速在1~4 s内波动幅度较方案1下降了78.4%,不良抖动明显减少。其主要原因在于由3级传动变为1级传动,减少了误差累积;
(2)方案2中输出齿轮的径向位移在加减速阶段出现了明显的过渡期,且整体振幅大幅下降至±0.007 mm以内,平顺性和传动精度有明显的改善;
(3)两种方案的啮合力峰值相差不大,但方案2加减速阶段过渡平顺、整体不规则冲击较少,同时由于齿轮齿条的重合度更高,故所受压强更小,以上均有利于提高使用寿命。

