“汤液经法图”系列研究之四:五味化合规律的数理分析*
金 锐,韩 晟
(1.首都医科大学附属北京世纪坛医院 临床合理用药生物特征谱学评价北京重点实验室 北京 100038;2.北京大学医药管理国际研究中心 北京 100191)
“汤液经法图”描述了一个基于五脏虚实和五味补泻的辨证论治体系,与仲景经方的配伍原则密切相关,且同时将脏腑辨证、中药药性、复方配伍等若干理论融于一体,具有重要的理论和实践价值。其中,五味补泻理论所示的五味与功效的关系(例如辛味能够补肝、泻脾和散肺),与传统药性理论关于五味功能的认知有所不同(例如辛能散能行),为科学理解辛味、甘味和苦味中药的功效特点提供了独特的启示意义。运用“汤液经法图”体系,可以直观、简明地还原中药组方配伍的基本原则。例如,理中汤由人参、甘草、干姜和白术组成,其中人参和甘草味甘补脾益气,干姜味辛泻脾止呕,白术味苦燥脾祛湿,四药联用共同形成补泻兼施、以补为主的脾胃病治疗组方,其中的君药当为人参。又如,五苓散由茯苓、猪苓、白术、泽泻和桂枝组成,其中茯苓和猪苓味甘泻肾利水,白术味苦补肾利湿,泽泻味咸润肾利水,四药联用共同形成以泻肾利水为主的肾膀胱病治疗组方,而桂枝味辛补肝,当与酸味五味子辛酸化甘,才可入肾化气除烦止咳,故五苓散中的“五”当为五味子。再如,从“汤液经法图”角度看,用于本次新型冠状病毒肺炎典型症状患者(咳喘憋闷、发热呕恶)的中医治疗方基本均以咸辛泻肺泻脾为主。其中,咸味药多用葶苈子、厚朴、甘草配苦杏仁(甘苦化咸),辛味药多用麻黄、藿香、半夏、草果等[1]。由此可知,“汤液经法图”提供了一套完整、实用、严谨的理论和实践体系,对于中药药性认知、复方配伍原理解读等中医药学基本问题的研究大有裨益。
实际上,“汤液经法图”体系的最特别之处,在于将3种药味对应于同一脏腑,分别视为补味、泻味和调和之味,且补味和泻味可以化合形成调和之味,即五味化合理论。例如,补肝的辛味和泻肝的酸味化合得到缓肝的甘味、补肾的苦味和泻肾的甘味化合得到润肾的咸味等[2]。那么,在五味化合模式中,为什么辛味与酸味化合得到甘味而不是咸味、苦味与甘味化合得到咸味而不是酸味呢?这是关于五味化合理论科学性的基本问题。笔者认为,这种化合有可能是真实滋味组合后的变化,但目前少有资料和研究证据。所以,本研究尝试从数理分析的角度,来论证这种化合结构的唯一性与确定性。
目前,应用于中医药基本理论研究的数学方法很多,大部分是数据挖掘方法,包括关联规则分析、聚类分析、神经网络算法等,而数学建模方法较少[3]。从研究对象上看,“汤液经法图”并不是包含大量信息的数据库或数据集,而是简明精炼的关系组合。从研究目的上看,五味化合理论不是概率统计的结果,而更像是先验的理论关系模型。所以,本研究选择数学建模和数理分析的方法进行论证。其一,选择能够代表两两关系的二维矩阵作为五味化合理论的数学表达,通过穷举法证明其唯一性。其二,参考经典图论“一笔画”问题,基于五行相生相克关系,论证五味化合理论的唯一性。
1 矩阵穷举法
1.1 五味化合矩阵R及内含规则
“汤液经法图”所示的五味配伍及化合关系如图1所示,其中,五边形每一条边外的文字代表了药味化合关系,分别为辛酸化甘、咸苦化酸、甘辛化苦、酸咸化辛和苦甘化咸。
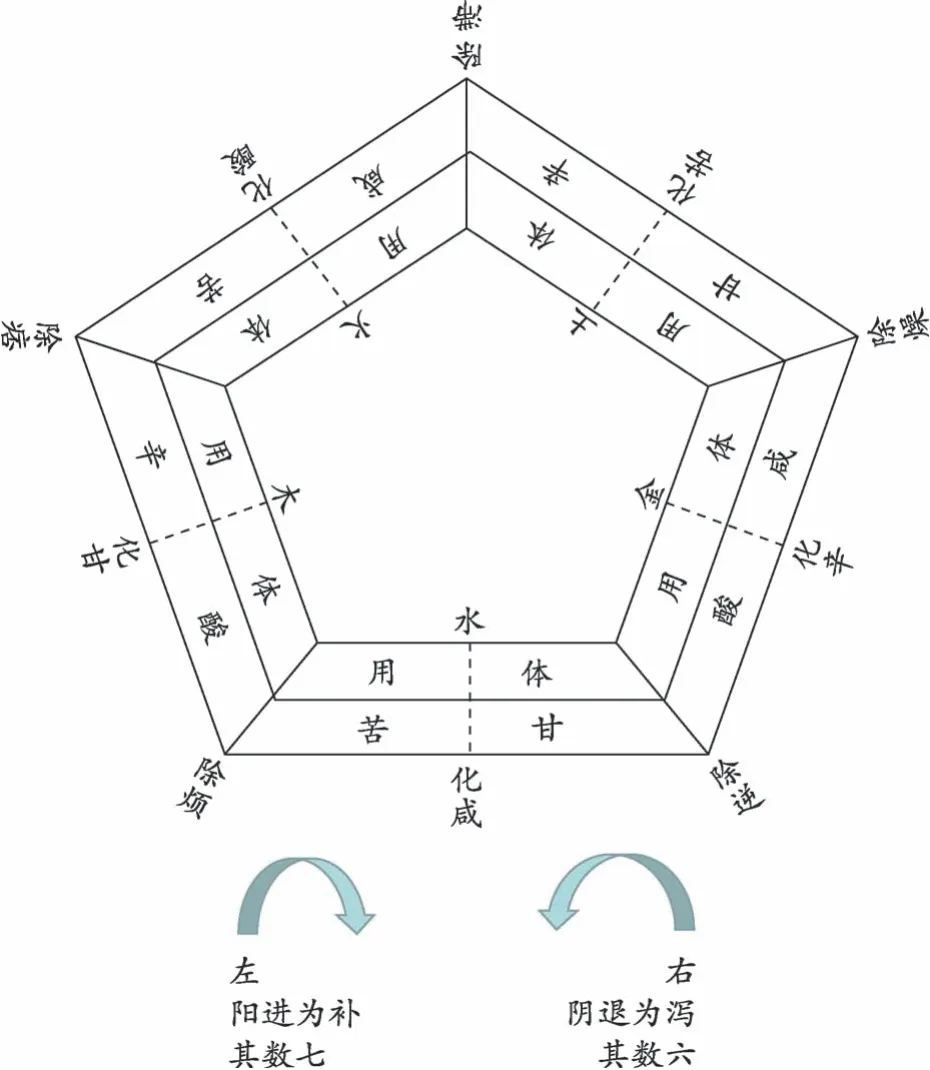
图1 汤液经法图
矩阵来源于方程组的系数及常数所构成的方阵,在中医五行理论的研究中有所应用[4-5]。本研究中,药味的化合关系属于两两关系,适合采用行列式矩阵进行研究。所以,本文建立5×5的矩阵R,来代表不同药味之间的化合关系。假设,采用数字1-5代表五味的属性值,其中,1代表辛味、2代表咸味、3代表甘味、4代表酸味、5代表苦味。如此便得到矩阵R,

其中,ri,j代表第i行与第j列之间化合后的属性值。如果存在化合关系,则以化合后的药味所代表的数字为属性值;如果不存在化合关系,则属性值为0;如果药味与其本身化合,则仍然以该药味所代表的数字为属性值。例如,r1,1为辛味与辛味化合,仍然为辛味,故其化合后的属性值为1。r1,2为辛味与咸味化合,“汤液经法图”中未记载此类化合关系,故其化合后的属性值为0。r1,4为辛味与酸味化合,辛酸化甘,故其化合后的属性值为3。根据该原则,可以得到矩阵R如下:

仔细分析,矩阵R有如下几个特点:
①规则一:有且仅有矩阵R的对角线,体现五味本味的属性,即ri,j(i=j)=i。进一步拓展得到ri,j(i≠j)≠i或ri,j(i≠j)≠j。也就是说,本味与他味化合,不可能再得到本味,“辛酸化辛”或“辛酸化酸”的组合是不存在的。关系符合均衡的分配律。药味化合不存在重复,“辛酸化甘”与“辛咸化甘”不可能同时出现。

③规则三:矩阵R是一个对称矩阵,即RT=R。这体现出,药味化合没有先后之分,“辛酸化甘”与“酸辛化甘”的含义完全一样。
④规则四:矩阵R的元素分布呈现出平行律。即(1-2)和(3-4)两对元素组合,在分布上呈现平行于对角线的斜向右下分布。这体现出,从原图顺时针或逆时针的角度看,药味化合后的合成药味分布,与原有药味的分布结构相同。
⑤规则五:矩阵R的元素并不是简单的数字,其本身就具有相生相克关系。例如,1代表辛木,2代表咸火,木生火,所以1与2存在相生关系。
Hold住萌 坑爹 给力 围观 你懂的 肿么了 有爱 神马浮云 吐槽 蛋疼 达芬奇的眼泪 啥都有 円族 有木有 云电视 伤不起 我勒个去 谣盐 你妹 腐女 普通青年 文艺青年 2B青年 隐蔽青年 SKI族 妥妥的 虎妈 高压锅族 驴友 微电影 加名税 尼玛 小清新 此处省略一万字 闪玩 求干货 拇指消费 地沟油 癌症性格 冻脸效应 悲催Peak people Cyberflaneur Linsanity NC AFK Eurogeddon Drynuary
上述5个规则,是五味化合理论转化为矩阵R后,必须满足的基本条件。
1.2 穷举法寻找满足上述原则的矩阵S
接下来,假设存在同样满足上述条件的矩阵S,来代表除此之外的另一种五味化合结构。并采用穷举法,确定矩阵S的结构。
第一种情况,令:


第二种情况,令梯形框区域内的数值两两调换,共有C25=10种情况。分别得到矩阵SS1,SS2……SS10,并分析其与规则一、规则二与规则三的符合情况。结果见表2。

表2 SS矩阵与规则的符合度情况
分析可知,第二种情况,将属性值两两直接调换的10种矩阵SS,均违反了规则一。所以,矩阵SS1-SS10不存在。
理论上看,除了两两直接调换,还可以通过n个属性之间(n≥3)的组合实现同步调换。因此,从单向调换的方式看,5种属性值的调换,包含了A25=20种单向变换方式。根据表1结果可知,在这20种单向变换方式中,有10种不能进行的单向变换。以符号“⇒”代表不能进行的位置变换,可得到这10种不能进行的单向变换分别为:2⇒1,1⇒3,4⇒1,1⇒5,3⇒2,2⇒4,5⇒2,4⇒3,3⇒5和5⇒4。除此之外,以“→”代表能够进行的单向变换,分别为1→2,1→4,2→3,2→5,3→1,3→4,4→2,4→5,5→3和5→1。也就是说,矩阵S只能通过在左下角和右上角的2个区域,通过组合以上10种能够进行的单向变换来获得。于是,第三种情况,将左下角和右上角梯形区域内的5个数,通过首尾相接地组合上述10种能够进行的单向变换,得到矩阵SSS。根据排列组合规律,以从1出发至从5出发的顺序,逐一列出首尾相接的组合共12种。其中,三个属性值首尾相接的组合5种,四个属性值首尾相接的组合5种,五个属性值首尾相接的组合2种。构建SSS1-SSS12,并考察其与规则四的符合程度,结果如下(表3):

表1 R矩阵所表达的内容

表3 SSS矩阵与规则的符合度
实际上,规则四只是矩阵R平行律的部分展示,通过将R进行加法拓展形成R2,就可以更好的展示这种平行律。可以看出,在R2矩阵中,任意左上斜向右下的对角线,都按照1、2、3、4、5的顺序排列,而SSS3、SSS6和SSS12都不符合这种平行律。所以,在SSS2、SSS3、SSS6、SSS7和SSS12这5个无法判断的矩阵中,通过拓展即可发现,只有SSS2和SSS7符合上述所有规则,也满足拓展后的平行律。

从规则一到规则四的角度看,SSS2和SSS7均同时满足所有规则。但是,如果从规则五的角度看,矩阵中的数字并不是简单的数字,而是蕴含着原有的五行相生相克关系,1-2-3-4-5构成了一个“木-火-土-金-水”的相生循环。所以,矩阵中数字顺序(从小到大)能够代表相生的五行关系。而五味化合理论实际上也是一种特殊的相生关系,是一种两两结合生它味的相生关系。因此,为了避免重复,两两化合所得到的药味,不应该是其中某一药味对应五行的所生之味。从数学表达式角度,

分析可知,矩阵R符合上述规则,而对于矩阵SSS2,由于SSS1,4=2,故SSS2不符合上述规则。对于矩阵SSS7,由于SSS1,3=2,故SSS7不符合上述规则。综上所述,符合规则的矩阵有且只有R本身,故其具有唯一性。也即,五味化合理论的化合模式和顺序具有唯一性。
2 图论分析法
2.1 “一笔画”问题的由来及应用
“一笔画”问题起源于1735年的哥尼斯堡七桥问题。在哥尼斯堡的一个公园里,有7座桥将普雷格尔河中两个岛及岛与河岸连接起来,人们希望能够从岛或者河岸中任一块地方出发,恰好通过每座桥一次,再回到起点。欧拉于1736年研究并解决了此问题,他把问题归结“一笔画”问题,证明上述走法是不可能的[6]。实际上,任意能够“一笔画”完成的图形必须具有2个特点:①图形的各部分都是有线相连的,即它是连通图;②图形中的奇点(相连的边的个数为奇数的交点为奇点,相连的边的个数为偶数的交点为偶点)个数为0或2。只有同时满足上述两个条件的连通图,才可以一笔完成(笔不离开纸面),这就是“一笔画”原理。“一笔画”原理是图论和拓扑论的基础,具有重要的学术地位。目前,在邮递员路线设计、工业船体零件切割、伤口类型的法医学鉴定等方面[7-9],都有“一笔画”原理的应用。
2.2 五角星图形“一笔画”方法与五味化合理论的唯一性
从抽象概念上看,“一笔画”原理实际上描述了由点和线组成的连通图内,点与点之间,或者线与线之间的关联关系。换句话说,“一笔画”原理可用于研究点与点之间或者线与线之间的先后排序关系。基于这一点,笔者发现,五角星图形就是一个包含5个节点但奇点数为0的连通图,符合“一笔画”原理。通过对五角星图形的“一笔画”方式进行分析,有助于认识五个顶点的关联关系。具体方法如下:在中心对称的五角星图形中,以A、B、C、D、E标示出5个顶点。同时,将五行和五味属性依照五行相生的顺序顺时针标示于五角星图形的5个顶点(图3),即从A到E分别为辛木、咸火、甘土、酸金和苦水。由于本研究仅讨论顶点之间的关联关系,故设定以下条件:

图3 五角星图形及“一笔画”途经
①条件一:“一笔画”由某顶点出发,在该顶点结束。
②条件二:任意顶点之间必须以最短线段连接。
根据上述2个条件,可以采用“一笔画”原理完成图2,例如从A出发,顺序经过C、E、B、D,再回到A,构成一个完整的五角星图形,即“一笔画”途经为A-CE-B-D-A。如果将顶点的五行五味属性代入这个“一笔画”途经,则得到辛木-甘土-苦水-咸火-酸金-辛木的循环顺序。仔细分析可知,在这个循环顺序中,前后相邻的2个属性是相克关系,具体为前位属性克后位属性。例如,在“辛木-甘土”的组合中,木克土;在“咸火-酸金”的组合中,火克金。而前后相邻的3个属性就是五味化合理论关系,即前2个属性的化合得到第3个属性,例如,在“辛木-甘土-苦水”的组合中,辛甘化苦;在“苦水-咸火-酸金”的组合中,苦咸化酸。实际上,在A-C-E-B-D-A的“一笔画”途经中,任意相邻的3个属性都恰好构成五味化合理论。
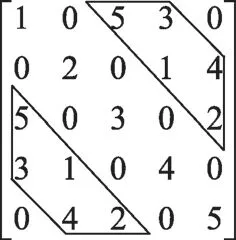
图2 矩阵可调换的区域示意图
据此,将符合条件的10种“一笔画”途经全部列出,并分析其中相邻2个属性、相邻3个属性的生克关系(表4)。由此可知,在全部10种五角星图形的“一笔画”途经中,前后相邻2个属性均具有相克关系,前后相邻3个属性之间均具有五味化合关系,不存在其他关系。同时,根据“一笔画”出发时选取的不同路线,10种途经可分为2类,一类是正向克制和化生的顺序(前克后,化生末位属性),另一类是反向克制和化生的顺序(后克前,化生前位属性)。

表4 完成五角星图形“一笔画”的不同画法
实际上,从正向化生的“一笔画”顺序看,由顶点A(辛木)出发,经过顶点C(甘土)的“一笔画”路线,下一站必须是顶点E(苦水),绝无可能是顶点B(咸火)或顶点D(酸金)。换句话说,辛木与甘土的化合,必须生成苦水,不可能生成咸火或酸金。同理,换成任意一个顶点都具有上述规律。所以,五行五味之间的化合关系是固定“锁死”的,是唯一的。
3 小结与展望
在一般的五行内涵中,相生相克是最基本的五行关系,也是全部的两两关系,而3个属性之间的关联关系却极少涉及。而《辅行诀五脏用药法要》收载“汤液经法图”中所标示的五味化合理论,正是这种3个属性之间关联关系的经典表述,体现了五行属性之间的固定规律。这种固定规律是客观存在的,选择合适的数学模型和方法,思辨性地抽象,就可以窥其一角。本研究选用代数学的矩阵理论和几何学的传统图论,从穷举法的角度,证明了这种固定规律的唯一性,为基于五味化合理论的中药组方配伍原理研究奠定基础。目前来看,“汤液经法图”和五味化合理论在新型冠状病毒肺炎中医治疗方的分析中已经有所应用[1]。
从某种意义上看,五味化合理论背后的五行属性化生关系,似乎是在五行相生和相克之外的另一种关系,或者是描述五行相生与五行相克之间关联性的一种关系,值得深入探究。从概念的内涵和外延角度看,概念的内涵,就是概念所反映的事物的特有属性,即概念的本质;概念的外延,就是具有概念所反映特有属性的事物,即概念的适用范围。内涵与外延成反比关系,内涵越小,外延越大。五味化合理论所体现的五行属性关系,它的内涵很小,外延很大,除了目前见到的五味化合理论之外,应该还有更多与五行属性相关概念范畴的应用,例如五色、五音、五畜等,值得进一步探索挖掘。
——以“收”为主 多酸少辛
——识记“己”“已”“巳”

