具有不同节点刚度的装配式框架结构在不均匀沉降下的内力响应分析

郑雯，刘振文，秦涛，李克先，侯良英，于广明

(1.青岛理工大学 土木工程学院，山东 青岛 266033；2.山东省高等学校蓝色经济区工程建设与安全协同创新中心，山东 青岛 266033；3.黑龙江科技大学 矿业工程学院，黑龙江 哈尔滨 150022；4.青岛市地铁一号线有限公司，山东 青岛 266071；5.华诚博远工程技术集团有限公司 青岛分公司，山东 青岛 266011)

随着我国大力推广装配式框架结构建筑，装配式框架结构的节点连接刚度也成为其设计和施工过程中的重点问题。国内学者对装配式框架结构进行了大量研究，其中吴从晓、赵斌等[1-2]对预制装配式混凝土框架结构的滞回特征、位移延性、承载能力和强度退化的抗震性能进行了试验研究与模拟；李世达、王俊等[3-4]表明装配式混凝土框架柱-柱节点连接可按照现浇混凝土节点进行设计；刘颖等[5]建立装配式框架结构在竖向荷载作用下的内力计算方法，得到受半刚性节点的影响梁端弯矩有所降低，而跨中弯矩增加；屈克达等[6]对单层两跨混凝土框架进行加载实验，并与有限元模拟对比分析，得出框架节点的相对转动刚度的大小可以按初始相对刚度的70%～80%进行计算；鲁浩[7]利用相对刚度比及相对转动刚度得到半刚性节点的区间范围，且通过有限元软件模拟静力、动力状态来研究半刚性节点对装配式框架结构的内力、侧移刚度的影响规律。本文在以上研究基础上,对不同节点连接刚度的装配式框架结构在不均匀沉降作用下的内力进行响应分析，为装配式框架结构的设计、施工以及安全维护提供研究依据。

1 对比模型的建立

本文以层数和跨数为参数变量，利用Midas Gen建立四种工况模型进行分析，选取梁截面尺寸为300 mm×500 mm，柱截面尺寸为600 mm×600 mm，6 m为一跨，每层柱高为3.9 m，梁柱均为弹性模型，选用C30与C40两种规格的混凝土分别作为梁与柱的材料，材料参数见表1。

表1 模型材料物理力学参数

建立工况S1：单层单跨模型，如图1(a)所示；工况S2：五层单跨模型，如图1(b)所示；工况S3：两层双跨模型，如图1(c)所示；工况S4：五层双跨模型，如图1(d)所示。模型柱脚视为刚接，通过释放梁端约束来改变节点连接刚度。在单跨的模型中给右柱施加12 mm竖向位移荷载，在双跨模型中给中柱施加12 mm竖向位移荷载，以保证两根柱之间沉降差保持不变。模型研究中只考虑节点连接刚度与竖向位移荷载对梁柱的内力影响，不考虑其他作用荷载对梁柱产生的影响。

2 不均匀沉降下结构内力随节点刚度的变化规律

本文通过改变梁端约束刚度进行模拟，即在Midas Gen建模设置边界条件时，通过改变节点弯矩来达到模拟不同节点刚度的效果。在实际工程中，混凝土框架结构梁、柱节点域范围内存在一定的固接效应，即便对梁端刚度人为进行削减，其刚度及刚度域附近仍会保持一定的刚度，且在模型计算时，当节点刚度小于10 kN·m/rad及大于109kN·m/rad时，四种工况下梁柱内力基本保持不变，故选取节点刚度R为10～109kN·m/rad；为简化横坐标，将节点刚度取对数得到lgR为1～9。梁、柱内力随节点连接刚度的变化曲线如图2、图3所示。

(a) S1 (b)S2

对比分析图2四种工况,从图2 (a)和(b)可知，节点连接刚度对底层梁端弯矩的影响表现为：当梁柱节点连接刚度在10～104kN·m/rad范围内，四种工况下的弯矩变化值基本相同。在104～106kN·m/rad范围内，工况S1与S2弯矩随刚度变化趋势基本相同，工况S3与S4弯矩随刚度变化趋势基本相同，底层梁左端的上部一直处于受拉区，且弯矩值随节点连接刚度的增大而增大；同理，底层梁右端的下部处于受压区，且弯矩值随节点连接刚度的增大而增大；当节点连接刚度接近106kN·m/rad时，四种工况梁端弯矩值变化率减小。由于底层梁右端与沉降柱相连，在柱发生位移沉降时，梁需要克服自身重力下沉，因而底层梁左端弯矩值要比梁右端弯矩值大。

从图2 (c)和(d)可知，节点连接刚度对底层梁端剪力的影响表现为：底层梁左端剪力值曲线与右端的变化趋势相近，但梁左端剪力均为正值；底层梁右端剪力值有正负之分即有方向之分，当节点连接刚度较小时，剪力方向与竖向位移方向相反，当节点连接刚度接近104kN·m/rad时，剪力为零，剪力方向改变；当节点连接刚度接近106kN·m/rad时，四种工况中，底层梁端剪力值不随节点连接刚度的变化而变化，即梁柱节点到达刚接状态。

从图2 (e)和(f)可知，节点连接刚度对梁轴力的影响表现为：底层梁一直处于受拉状态，这是由于柱在下沉时，拉动梁下沉；工况S1与S2的轴力值基本趋于稳定；在工况S3和S4时，梁中出现最大正轴力。顶层梁一直处于受压状态，这是由各层累计变形过大引起，且在工况S3 时，受到的压力值最大。随着节点连接刚度变大，工况S3与S4中顶层梁轴力值要大于底层梁的，工况S1与S2中轴力值无论是底层梁还是顶层梁，变化值基本相同。从两图比较可以看出，底层梁轴力受层数的影响较为明显。

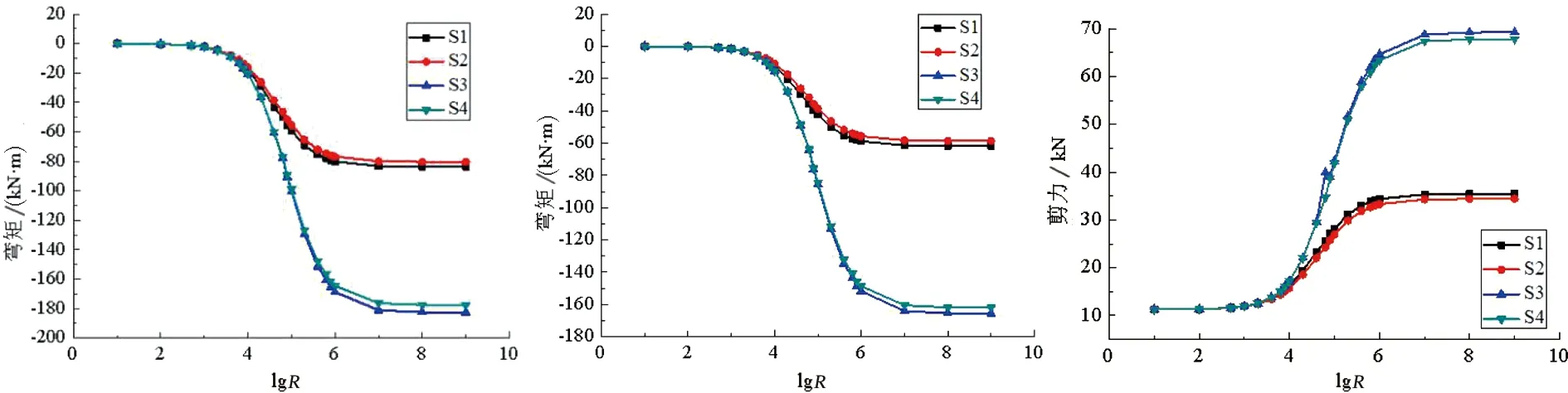
(a)底层梁左端弯矩 (b) 底层梁右端弯矩 (c) 底层梁左端剪力

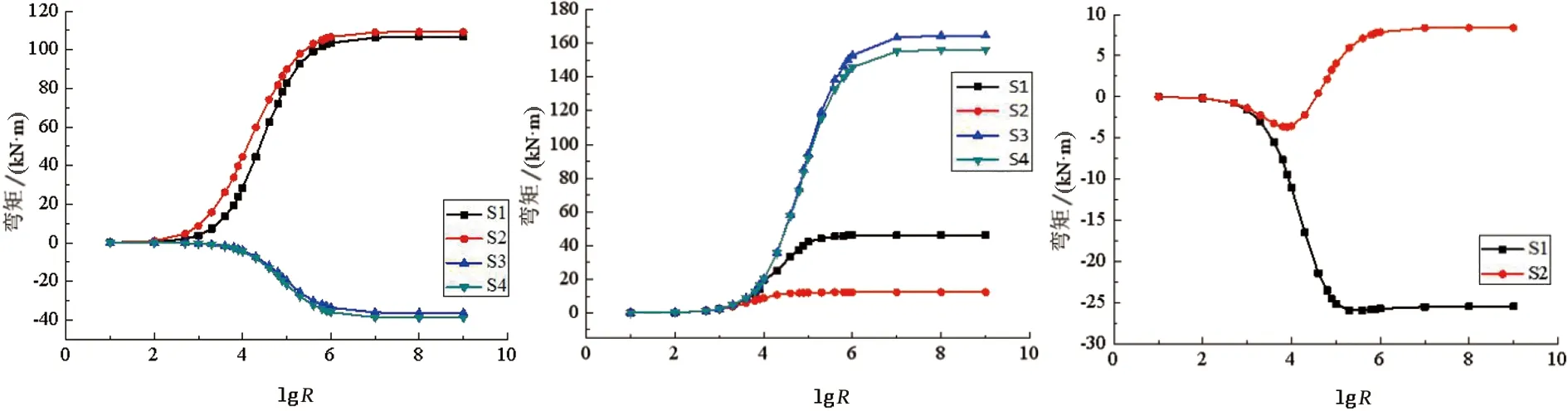
(a) 底层左柱柱底弯矩 (b) 顶层左柱柱顶弯矩 (c) 顶层沉降柱柱顶弯矩

从图3 (a)、(b)和(c)可知，节点连接刚度对柱端弯矩的影响表现为：工况S1、S2底层左柱柱底的受力状态与工况S3、S4的相反，且弯矩值要远大于S3与S4的；四种工况中，左柱柱顶受力状态相同，工况S2中，左柱柱顶弯矩受节点转动刚度影响较小，即沉降对单跨多层房屋顶柱的影响可以忽略不计。顶层沉降柱的弯矩变化比较复杂，工况S1在位移作用下，随着节点连接刚度增大不断增大，最后趋于稳定；但对于工况S2顶层沉降柱的弯矩在位移载荷作用下，柱外侧处于受拉区，当节点连接刚度为104kN·m/rad时，柱内侧出现压应力，随着节点连接刚度的增大，柱顶外侧又呈现受压状态。

从图3 (d)可知，节点连接刚度对底层剪力的影响表现为：工况S1与S2 剪力值变化不明显；工况S3与S4剪力值变化较为明显，在节点连接刚度接近106kN·m/rad时，两者间的剪力差值最大，相差4.2 kN。

从图3 (e)和(f)可知，节点连接刚度对底层轴力的影响表现为：对于底层左柱轴力，工况S1与S3、工况S2与S4曲线初始变化趋势相同，这是由于柱子轴力受到结构自重影响，同时可看出轴力值变化与层数有关；对于底层沉降柱的轴力值，在节点连接趋于铰接时，四种工况的轴力各不相同，但随节点连接刚度增大沉降柱由初始受压状态变为受拉状态；单跨结构柱在节点连接刚度不同时，由位移引起的轴力值变化不大，而双跨结构柱轴力值受到层数的影响较大。

3 不均匀沉降下结构内力系数随节点刚度的变化规律

3.1 内力系数随节点刚度变化的规律研究

传统的现浇式框架结构按照刚性节点进行设计，对于装配式框架结构节点,本文定义为半刚性节点，其设计原则目前没有规范明确规定，设计人员还是按照现浇式的原则对其进行修正分析，这种方法相对来说比较复杂，在各种外界条件影响下，计算难度也比较大。所以确定节点转动刚度系数在不同值时，结构内力值与刚性节点内力值之间的关系，这样可以简化计算。

框架结构内力系数计算公式为：

β=M/MF，

(1)

γ=V/VF，

(2)

η=N/NF，

(3)

式中：β、γ、η分别为弯矩系数、剪力系数、轴力系数；M、V、N是半刚性连接的装配式框架结构的内力值；MF、VF、NF分别为刚性连接的现浇式框架结构的内力值。

节点转动刚度系数为

α=EI/(LR)=ib/R，

(4)

式中：R为节点连接刚度；L为跨度，本文取6 m；EI为梁柱的抗弯刚度，可根据表1中梁柱混凝土的材料参数以及梁柱的尺寸进行计算。

通过式(4)得到梁的线刚度ib=15 625 kN·m。依据第二部分变刚度分析中定义的节点连接刚度，可以求得相对应的节点转动刚度系数。如图4、图5分别给出了梁、柱的内力系数随节点转动刚度系数的变化曲线。

(a)底层梁左端弯矩系数 (b) 底层梁右端弯矩系数 (c) 底层梁左端剪力系数

从图4可知：在不均匀沉降下，四种工况随着节点转动刚度系数α不同，底层梁端的弯矩系数、左端剪力系数、轴力系数及顶层梁轴力系数的曲线变化趋势相同，基本呈现为内力系数随α增大而减小，在节点转动刚度系数为0.78 时，下降速率缓慢减小，直到节点转动刚度系数到2.6 时，内力系数出现平稳状态；底层梁右端剪力系数随节点转动刚度系数增大由正值逐渐变为负值。在工况S1与S2中，在接近铰接状态时，梁右端剪力方向与竖向位移方向相反，随节点转动刚度系数增大，在位移荷载作用下剪力系数值逐渐减小，直到节点转动刚度系数为0.78 时，剪力方向改变，且剪力系数值逐渐增大，直至趋于刚接为止。

从图5 (a)、(b)和(c)可知，节点转动刚度系数对柱端弯矩系数的影响表现为：对于底层左柱柱底，工况S3与S4中，弯矩系数变化曲线基本相同；工况S1与S2中，弯矩系数出现明显差值；底层柱底在趋于刚接时弯矩系数基本相同，随节点转动刚度系数增大，四种工况弯矩系数值出现分离，但变化趋势基本一致。对于顶层左柱柱顶，四种工况弯矩系数值在节点连接趋于刚接时已经出现了分离现象，随节点转动系数增大四种工况的弯矩系数差值逐渐增大，直到节点转动刚度系数为4时，S3与S4两工况弯矩系数差值又开始逐渐接近。对于顶层沉降柱柱顶，弯矩系数受到层高影响比较明显，内力变化比较复杂，弯矩系数随着节点转动刚度系数增大而减小；在工况S2中，在节点转动刚度系数为0.78 出现弯矩系数为0的点，随后负值绝对值一直增大，在节点转动刚度系数到达2时，出现负值绝对值的最大值，然后缓慢趋向正值。

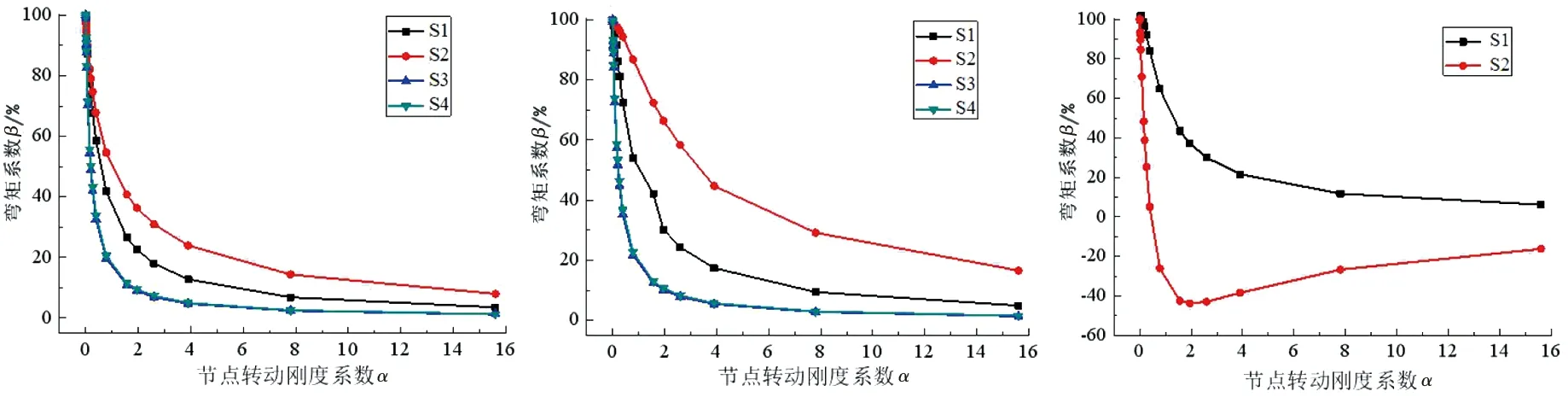
(a)底层左柱柱底弯矩系数 (b) 顶层左柱柱顶弯矩系数 (c) 顶层沉降柱柱顶弯矩系数

从图5 (d)可知，节点转动刚度系数对底层左柱剪力系数的影响表现为：四种工况剪力系数变化趋势基本相同，当节点转动刚度系数为0.78时，工况S1与S3出现差值，节点转动刚度系数接近8时，曲线再次出现闭合，工况S2与S4变化同上。即底层左柱剪力系数与结构的跨数有关，与层数无关。

从图5 (e)和(f)可知，节点转动刚度系数对柱轴力系数的影响表现为：在工况S3与S4中，底层左柱柱底轴力系数变化曲线基本一致，底层沉降柱柱底轴力系数在节点转动刚度系数为4时开始出现较小差值，可以忽略；工况S1与S2轴力变化曲线呈相反趋势，且沉降柱柱底的轴力系数要大于左柱柱底轴力系数。

从图5可知，柱内力系数变化与跨数有关，且在单跨结构中受层数影响较大。

3.2 弯矩系数与节点转动刚度系数的关系

通过半刚性节点与刚性节点之间的关系，求出半刚性节点框架结构的梁柱弯矩值，进一步可求出梁柱的剪力值与轴力值，本节只对弯矩系数进行研究。在进行计算时，由于半刚性节点的加载和卸载是一个复杂的过程，可以采用线性的弯矩-转角特征公式进行简化计算。节点相对转动刚度r是指在梁端承受弯矩的作用下，节点处柱端与梁端发生相对转动的角度θr所需要的弯矩M，如图6所示。

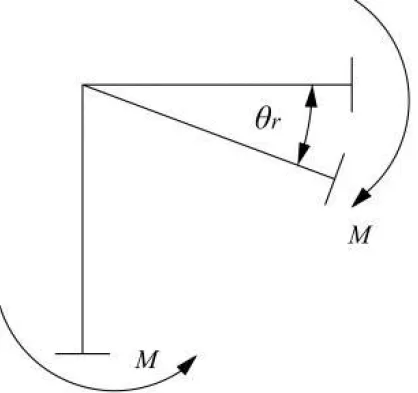
图 6 梁柱节点相对转动图

(5)

式中r为连接初始刚度，由弯矩-转角关系曲线或试验数据确定。

在文献[8-9]单跨框架受均布荷载计算基础上改进，进行本节计算，参数设定与3.1节相同。

图7为单层单跨框架计算模型图，图8为半刚性连接梁单元模型图，假定梁柱之间可以采用刚度为r的弹簧进行模拟连接，首先由结构力学推导在自重作用下半刚性构件连接引起的弯矩，假设梁A、B两端连接节点刚度R相同，转角分别为θA和θB。

图 7 单层单跨框架

图8 半刚性连接梁单元

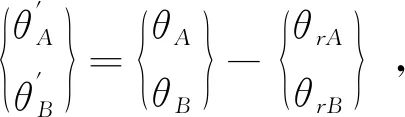
(6)

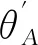
根据式(5)可得

(7)

因此连接部位的弯矩转角方程为

(8)

(9)

式中：MFA、MFB为刚性构件固定端弯矩。由式(8)可得

(10)

将式(6)代入式(9)得

(11)

联立式(10)和式(11)得

(12)

其中D=1+4αA+4αB+12αAαB，代入式(12)得

式中:

由于梁的参数性质相同，假定弹簧转动刚度相同，则令αA=αA=α，MFA=MFB=MF。

故根据式(13)、文献[8]及半刚性梁单元在支座移动下的内力计算方法，得到：

MAB=-lMF+mibθA+nibθB，

(14)

MBA=lMF+nibθA+mibθB，

(15)

MAC=kibθA，

(16)

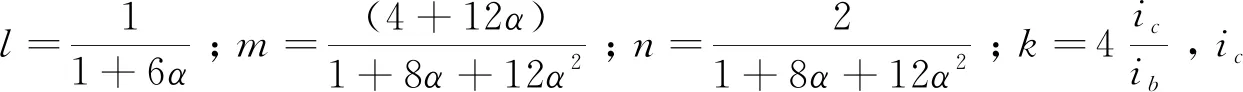
由于施加位移载荷，梁的两端产生的转角相同，则θA=θB，MAB=MBA，将条件代入式(14)可得

(17)

根据节点平衡∑MA=0可得

(18)

当α=0时，可以得到刚接节点的弯矩值

(19)

将式(19)代入式(18)可得

(20)

从而可以求出β与α之间的曲线关系，即

(21)

式中：α为节点转动刚度系数；β为弯矩系数。

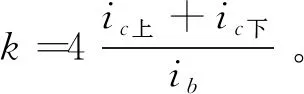
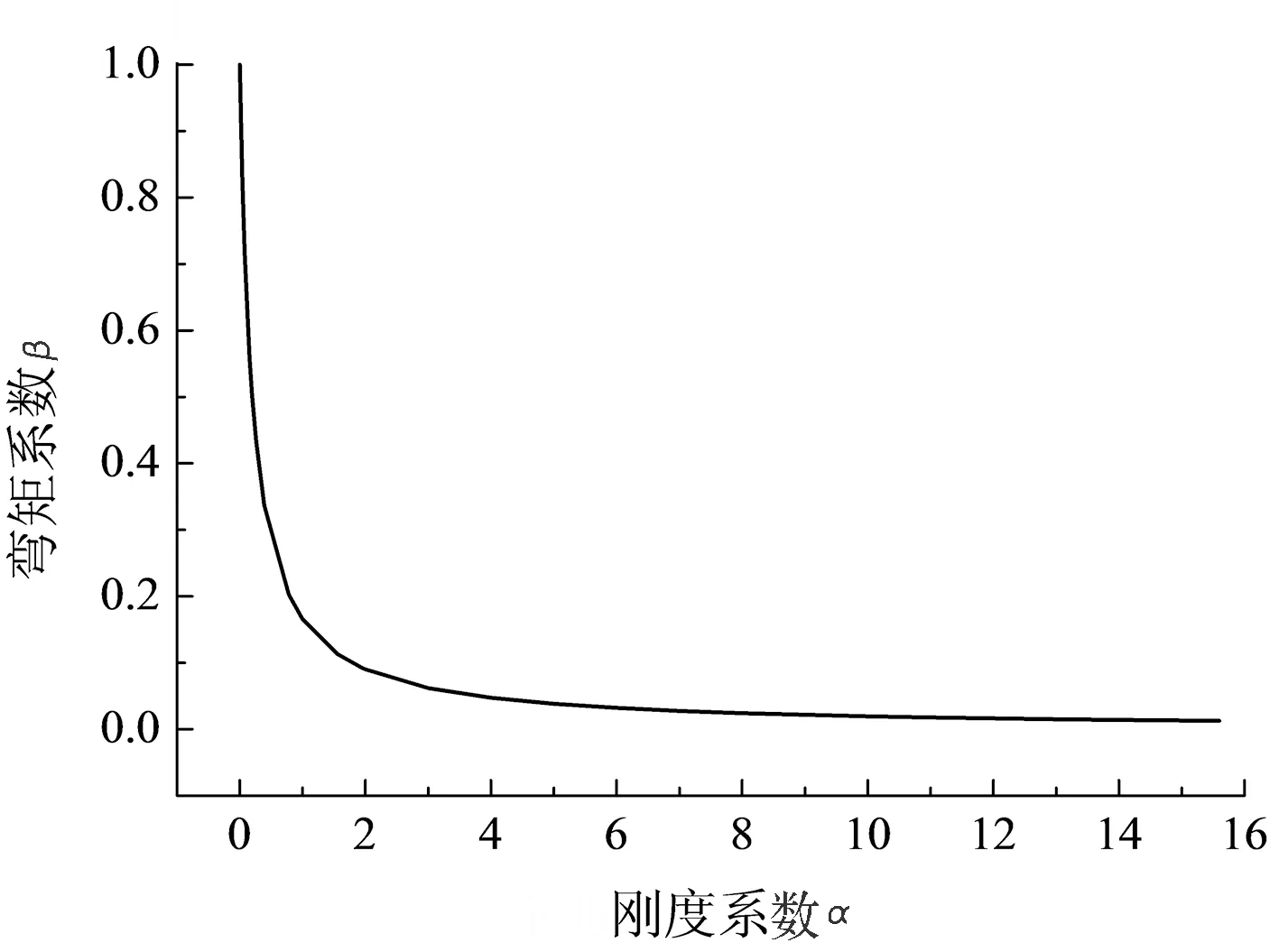
图9 梁端弯矩系数与节点转动刚度系数的关系曲线

从图9可以看出，此计算方法得到的梁端弯矩系数与节点转动刚度系数的关系曲线和本文用Midas Gen计算的曲线趋势是吻合的，但根据结构的跨数、层数、受力的不同，理论公式需要进行系数调整，故本方法不能精确计算构件的内力，但是可以适用于实际工程中判断构件的受力状态。

4 结论

本文采用Midas Gen建立四种工况模型，首先对比分析了不均匀沉降下半刚接的装配式混凝土框架结构与刚接的现浇式混凝土框架结构内力变化规律；然后研究了不同节点刚度和节点转动刚度系数的装配式框架结构在不均匀沉降下内力系数变化规律；最后选取单榀框架进行内力推导验证本文的内力变化规律。通过数据分析得出如下结论：

1)单跨结构弯矩、剪力受节点连接方式的影响大于双跨结构，柱轴力受力情况与跨数无关；半刚性节点传递弯矩的能力相对于刚性节点较差。结构的内力变化与节点连接刚度有关，节点连接刚度同时会影响弯矩的传递，在结构设计时注意挠度、稳定性的计算。

2)在柱间沉降差不变条件下，将节点连接刚度从铰接向刚接逐渐变化，发现节点连接刚度对框架柱的内力影响表现比较复杂，需根据具体工况进行分析。框架结构中内力开始在某个范围中变化比较平缓，中间某一阶段呈近似于直线的增长，最后趋于平缓，平缓曲线意为弯矩值不随节点刚度的变化而变化，即节点的铰接和刚接，故可知当节点连接刚度在8×103kN·m/rad时，构件内力完全呈现铰接模拟结果，当节点连接刚度在4×105kN·m/rad时，构件内力完全呈现刚接模拟结果。

3)梁的内力变化与跨数有关，与层数无关；柱内力变化比较复杂，但工况S3与S4基本吻合，说明柱内力与跨数有关，在单跨结构中，同时受结构层数影响。

4)单层框架结构弯矩系数与节点刚度系数之间的关系公式曲线与有限元分析的曲线相吻合，本文拟合曲线适用于预测实际工程中的结构稳定性分析。