B2O3/蓝宝石熔体热毛细对流的二维数值模拟
莫东鸣,裴江红
(重庆工业职业技术学院 机械工程学院,重庆 401120)
0 引 言
液封提拉法能够抑制界面热毛细对流,防止晶体生长过程中可挥发性成分的挥发、改善结晶过程中的热传递条件,在晶体生长领域中表现了极大的前景[1]。对于液封生长技术中的双层液体系统而言,由于两层流体界面处的热耦合和力耦合的复杂性,使得双层流体系统内的热对流过程变得非常复杂。近年来,越来越多的学者对双液层流体的热毛细对流不稳定性进行了研究。Li等[2-3]对有上自由表面的B2O3/GaAs、5cSt硅油/H20环形双液层系统进行了二维数值模拟,并且,他们还对环形双液层系统求解了渐进解[4-5]。结果表明,液封层可以大大增强系统的稳定性,双层流体的临界Marangoni数比同等条件的单液层大约两个数量级。其他学者对矩形双液层系统的流动稳定性进行了研究,Simanovski等[6-8]对垂直加热、固壁施加周期边界条件、并且界面有热源的矩形双层系统进行了二维数值模拟,结果发现界面处足够强的热源会导致流动分岔的产生。
Mo等采用线性稳定性分析[9-11]对上自由表面、上固壁条件下的环形双液层的5cSt硅油/HT-70的流动稳定性进行了研究,发现了在不同的半径比、深宽比、下液层与总液层厚度比条件下,系统出现了三种流动失稳现象,即轮辐状的热流体波、轮辐状和热壁处同波数流胞叠加的热流体波,以及三维稳态流动。
综上,以上的研究多针对于矩形池内双液层系统,较少研究环形液池的双液层系统;从研究工质对上看,则多有关于硅单晶、砷化镓晶体的生长,对于蓝宝石晶体——广泛应用于国防、电子技术、科学技术的重要技术晶体生长过程中的流动稳定性研究还鲜少报道。学者们对单液层、提拉法晶体生长过程中的蓝宝石熔体流动进行了数值模拟[12-14],但涉及到液封提拉法生长蓝宝石晶体的双液层系统流动数值模拟研究还未见报道。为此,本文以微重力条件下、上自由表面的环形液池中B2O3/蓝宝石熔体的热毛细对流为研究对象,可以丰富双液层流动系统非平衡热力学理论,更可获得液封提拉法生长蓝宝石晶体的工程指导建议。
1 物理模型及求解方法
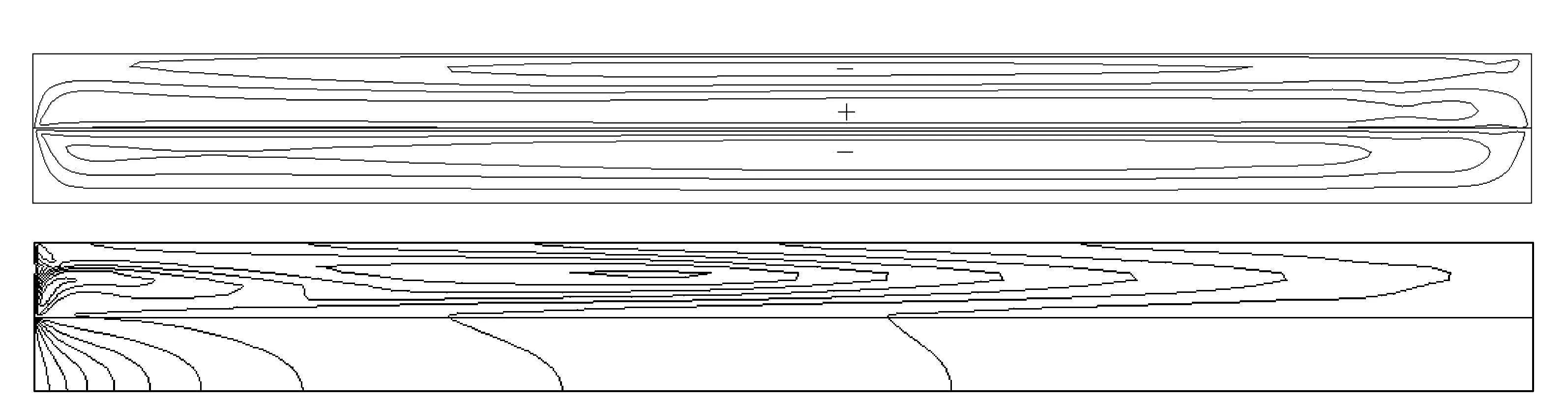
双层液体施以水平温度梯度,内壁为低温Tc,外壁为高温Th(Tc 图1 物理模型 在模型中引入如下假设:(1)熔体和液封均为不可压缩的牛顿流体,满足Boussinesq近似;(2)流速较低,流动为轴对称二维层流;(3)两相界面平整无变形,在自由表面、液液界面考虑热毛细力的作用,固-液界面满足无滑移条件;(4)底部边界绝热;(5)表面张力是温度的线性函数。 对控制方程进行无量纲化,时间、长度、速度、压力无量纲尺寸如下: (ro-ri)2/n1,ro-ri,n1/(ro-ri)和r1n12/(ro-ri)2,则无量纲方程可写为: ∇·Vi=0 (1) (2) (3) 其中,ρi,ai,bi和νi分别为i(i=1,2)层液体的密度,热扩散系数,体积膨胀系数,动力粘度;Vi代表无量纲速度矢量;Qi=(Ti-Tc)/(Th-Tc))为无因次温度;Pi为无量纲压力;t为无量纲时间;ez为垂直方向的速度矢量;Pr=n1/a1为熔体的普朗特数。 在Z=H1=h1/(ro-ri)的液液界面边界条件为: (4a-c) 液封顶部,ri≤r≤ro,z=h的自由表面边界条件为: (5a-c) 其中,R与Z为无量纲坐标,Ma是Marangoni数,其定义式为Ma=g2-1(Th-Tc)(ro-ri)/(m1a1),m为动力粘度,k为导热率,g2-1=-∂g/∂T是流体的界面张力梯度。 径向与纵向速度用无量纲流函数y定义如下: (6) 在微重力环境下,由于浮力引起的自然对流的消失,热毛细对流将占据主导作用,这将可以获得一个相对理想的静态生长体系,热量和质量运输均被抑制,生长过程变成受限于扩散过程,这样的体系非常适合研究晶体生长、缺陷形成和溶质分凝,并且适合验证有关晶体生长机理的理论模型。为了认清熔体热毛细对流的温度场和流场的基本特性,本节将通过数值模拟的方法,以获取系统流动的流动特征、流动失稳的临界参数,以及失稳后的流动振荡流型。 液封提拉法生长蓝宝石晶体多采用B2O3作为液封流体,蓝宝石熔体与B2O3的物性参数同文献[2,15],见表1。 表1 B2O3与蓝宝石熔体的物性参数 当给双液层系统施加水平温度梯度,且Marangoni数低于临界值时,双液层系统中的热对流为轴对称流动。在上部为自由表面的环形池中,双液层系统的稳态流动表现为在R-Z截面上熔体层中流体逆时针旋转的单胞稳态运动,液封层中两个旋转方向相反的稳态流胞。靠近液液界面的流胞是顺时针旋转,靠近自由界面的流胞是逆时针旋转,这是因为它们都受到液液界面与自由界面处的热毛细力的拽引,而产生了热毛细对流。图2为微重力条件下,Ma=8.0×104时,Γ=0.2,ε=0.5,η=0.10时的流函数分布与温度分布。值得注意的是,从温度分布图上看,在靠近冷壁处的液封层,在近液液界面处,出现了一个长度约为径向总长度1/8长的高温区域,这是因为液液界面拽引的热壁处的高温流体在冷壁处回流,流速降低,形成了一个小区域的高温段。而当冷热壁温度进一步增大,即热壁处的温度进一步增大时,则此区域的温度就会越高,当温差达到一定程度时,则在液封层与熔体层出现了Marangoni对流,其对流强度高于径向的热毛细对流,就会出现从冷壁处向热壁处涌动的与液液界面热毛细对流方向相反的“逆向流”,如图3(j)、图3 (k)所示。 图2 稳态流动的流函数(上)与温度分布(下),Γ=0.2,ε =0.5,η=0.1,Ma=8.0×104, δψ=ψmax/10,Ψ(+)=0.015,Ψ(-)= -0.010,δΘ=0.1 图3 失稳流动的等流函数线Γ=0.2,ε =0.5,η=0.1,Ma =8.0×105,δψ=ψmax/10 图3为二维数值模拟获得的流动失稳后的R-Z截面流函数分布,可以看出,当Ma=8.0×105时,在近热壁处逐渐出现了振动流动,由于有液液界面处的热毛细力的拽引,流动从热壁处向冷壁处发生,表现为液封层有双层、顺逆时针交替滚动的流胞,随着流动的进行,这些液封层近热壁处的小流胞逐渐在垂直方向扩大流动范围,并由热壁处向冷壁处径向流动大概约2/3径向长度,如图3(a)-图3(i)。之后,由于高温回流在冷壁处聚集,在冷壁处产生垂直方向的温差,故在液封层与熔体层发生Marangoni流动,表现为从冷壁处向热壁处快速流动的单个流胞,如图3(j)、图3(k)所示。随着这些大流胞流向热壁处,冷壁处的高温流体也被带离冷壁处,垂向温差减小,Marangoni流动减弱,热毛细对流又占据上风,则再一次出现热毛细对流,形成周期流动。 为了解流动速度与温度的周期性变化,探寻流动失稳机制,本文监测了液-液界面、R=0.5处的监测点A,自由界面、R=0.5处的监测点B的径向速度与温度,如图4所示。从图上可以看到,径向速度波动和温度波动是不同步的,两者之间的相位差与热流体波运动方向有关。速度波动早于温度波动。从图4(a)与图4(b)的径向速度波动规律来看,两者的波动是呈相反趋势的,这是因为液液界面和自由界面都有热毛细力,它们驱动了液封层两个旋转方向相反的流胞在液封层旋转。但是,它们并不像5cSt硅油/HT-70的周期失稳呈现为周期性的等幅波动,而是出现一个速度比较大的类余弦波动后,又有一段较低速的径向流动,径向速度表现为负值,则为热壁向冷壁的流动,说明在这个阶段是热毛细对流阶段,当自由界面出现正向径向速度值、液液界面出现负向径向速度大值时,则对应冷壁处产生的Marangoni流动,向热壁处以单胞流动。 图4 Γ=0.2、ε=0.5和η=0.1,Ma=4.0×106时,不同监测点A、B处径向速度(实线)和温度(虚线) 本文研究了微重力条件,水平温度梯度作用下,上部为自由表面的环形双液层B2O3/蓝宝石熔体系统的热毛细对流流动稳定性,获得了以下结论。 (1)当Marangoni数较小时,流动为稳态流动,其表现为液封层有两个旋向相反的流胞,熔体层表现为一个逆时针旋转的流胞。 (2)随着Marangoni数超过流动稳定临界值,稳态流动变为周期振荡流动,表现为从热壁处向冷壁处扩展的多个旋向相反的小流胞,当扩展到径向长度2/3R处时,近冷壁处上、下液层产生单个流胞,并向热壁处逆向流动。 (3)振荡流动时,径向速度波动先于温度振荡波动。在一个周期流动中,先产生热毛细对流,再产生近冷壁处的Marangoni对流。
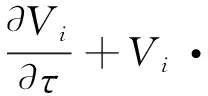
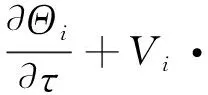
2 结果与分析


3 结束语

