换电模式下电动车货运路径优化模型与算法

李 进，王 凤，杨沈宇

（1.浙江工商大学管理工程与电子商务学院，杭州 310018；2.浙江工商大学现代商贸研究中心，杭州 310018）

（∗通信作者电子邮箱jinli@mail.zjgsu.edu.cn）

0 引言

物流行业具有高能耗和高碳排放的特点，如何构建新型低碳环保的物流体系是物流业发展的必然趋势。当前汽车碳排放约为我国总碳排放的25%，预计2030 年汽车二氧化碳排放量将达到423 亿吨。推广应用新能源车，加速燃油车替换是减少二氧化碳排放的必由之路。随着城市限行和国家推动货运用车电动化，我国明确提出提高电动车城市配送推广应用力度，2020年全国电动物流车产量达到10万辆。电动车在物流货运领域的应用对于我国节能减排和提高环境和经济效益都具有十分重要的意义。为此，本研究将换电式电动车作为运输工具，探究物流货运过程中碳排放核算及其低碳路径优化。

经典的车辆路径问题（Vehicle Routing Problem，VRP）［1］往往只考虑经济因素，以行驶距离、时间或成本最小为优化目标。低碳车辆路径问题则关注车辆行驶过程中产生的碳排放对环境的影响，在考虑能耗和碳排放的基础上建立车辆路径优化模型，越来越多的学者开始重视这方面的研究。早在1985 年，Cermak 等［2］就开始研究考虑城市气体污染防控的物流配送问题。Bektaş等［3］提出了污染路径问题，建立了考虑温室气体的排放、油耗和旅行时间等因素的基于混合整数规划的数学模型，提出了将非线性问题转化为线性规划问题的解决方案。Behnke等［4］研究了城市配送中考虑多车型和复杂交通网络的最小化排放的车辆路径问题，提出了一种列生成的有效求解算法。Turkensteen［5］在可变速度下对车辆路径优化中的传统油耗和碳排放计算模型进行了验证，发现速度波动相较于固定速度的计算方法油耗可能增加高达80%。李进等［6］建立了碳交易机制下的物流配送路径优化模型，分析了碳交易、碳价格和碳配额对配送路径策略、碳排放量和总成本的影响。周鲜成等［7］研究了时间依赖型绿色车辆路径问题，构建了考虑车辆油耗、碳排放、旅行时间以及固定起用成本等为目标的模型，并对蚁群算法进行改善设计。

目前在车辆路径问题研究中，很少有学者将电动车作为运输工具。根据目前电动车充电的模式、与电动车匹配的基本设施，现有研究主要将其细分为三个角度来研究:充电型电动车路径优化、换电型电动车路径优化以及电动车充换电站选址优化。在充电型电动车路径优化方面，Conrad 等［8］构建了充电型电动车路径优化模型，实现了电动车使用成本和货运成本的最小化。Hiermann 等［9］考虑了电动车的不同类型和时间窗约束，构建了最小化车辆数和行驶距离的电动车路径优化模型。Pelletier 等［10］提出了考虑不确定能耗的电动车货运路径优化问题，在大规模邻域搜索基础上提出了一种两阶段启发式算法。Bahrami 等［11］研究了插电式混合动力车辆路径问题，以总能耗最小为目标建立了一种能源管理模型，提出了一种精确的分支定价法和一种启发式算法。葛显龙等［12］研究了带软时间窗的电动车辆路径优化问题，建立了最小化路径成本、时间窗惩罚成本和车辆使用成本的数学模型，设计了融合节约里程和禁忌搜索的混合算法。

在电动车充电站选址与车辆路径问题方面，现有文献主要是将充电站的选址与电动车路径进行集成规划。例如:Yang 等［13］比较早地研究了基于电动车的网络选址与车辆路径联合问题，该问题考虑了电动车的容量约束和换电站的布局，设计了相应的启发式算法和禁忌搜索算法。杨珺等［14］将换电站选址和电动车路径优化进行集成研究，提出了一个混合整数规划模型，设计了一种改进的禁忌搜索智能求解算法，通过数值仿真对电动车容量、续航能力和固定建设成本等进行了参数敏感性研究。Worley等［15］也研究了电动车充电站选址和电动车路径优化相结合的问题，建立了考虑电动车续航里程和容量的一个整数规划数学模型。

将电动车作为物流运输工具，符合我国能源结构调整和物流车辆电动化的要求，研究和分析物流配送的碳排放和能耗节约情况具有很强的实际应用背景。目前换电式电动车具有充电快、安全性高和续航长等优点，传统的研究大多关注慢充或快充等充电方式的研究，对于物流企业具有车辆数量、电池续航能力和换电站等约束下以节能减排为目标的换电式电动车路径优化问题，目前这方面的研究还比较缺乏。由于车辆的碳排放与能耗有关，而能耗受到车辆速度、载重和距离等多种因素的影响，因此该研究还将建立换电式电动车的碳排放度量模型。总之，将换电模式下的电动车作为物流货运车辆，在路径优化中加入对能耗和碳排放的考量，该问题称之为换电式电动车货运路径优化问题（Battery-swapping Electricvehicle Freight Routing Problem，BE-FRP）。同时，针对该问题是NP-hard 难题［16-17］，提出能够满足计算机实时计算要求的基于爬山优化和邻域搜索的自适应遗传算法。该算法的交叉和变异概率随着种群的适应度变化而自适应调整，通过爬山优化加强了算法的局部搜索能力，提出了电动车换电站邻域搜索策略以满足电动车的电池续航容量和换电站约束，从而最终求得模型的最优解。通过数值实验验证了所提自适应遗传算法能够快速有效地求得满意的可行解，确保经济成本和碳排放量的最小化。

1 BE-FRP模型的建立

1.1 问题描述

文中定义的数学符号如下:完全有向图G=(V，E)表示货运配送网络，其中:V=C∪F为节点的集合，C={1，2，…，n}为客户点集合，F={0，n+1，n+2，…，n+}为换电站的集合，节点0 表示配送中心，假设配送中心也设有换电站+1为最大可用换电站数，E={(i，j)|i≠j∈V}表示弧集；K={1，2，…，}表示电动车队集合为最大可用电动车辆数，电动车的载重容量为Q；dij表示弧(i，j)的距离；vij表示车辆从节点i出发访问弧(i，j)的行驶速度；pij表示电动车访问弧(i，j)的耗电量；lij表示电动车辆在弧(i，j)的货物载重量；sf为电动车在换电站f的换电服务时间，f∈F；qi表示客户点i的货物需求量，i∈C；T为电动车的电池容量；xijk表示若电动车辆k访问弧(i，j)，则其值为1，否则其值为0；yijk表示电动车辆k访问弧(i，j)后的剩余电量。决策变量为xijk。

不同于传统的燃油车辆路径问题，经典的VRP 往往只允许车辆访问一次客户点，BE-FRP将换电式电动车作为运载车辆，加入了换电站，为了通过换电完成配送，电动车允许访问同一换电站多次，同时还将考虑换电站和电池续航能力约束。定义电动车每小时的使用费用为α，电动车使用费用与行驶时间正相关，包括司机薪酬、过路过桥费等；电动车消耗每度电的费用为β。BE-FRP 将优化电动车辆和路线安排使得电动车使用费用和能消耗总成本最小化。此外，还应满足如下条件:配送货物时，电动车从配送中心发出，配送完成后最终返回配送点；每个客户点被访问且仅被访问一次；换电站可被访问多次；每条配送路线的总需求不超过电动车的容量限制；电动车辆具有电池续航能力限制。

1.2 综合多种因素的电动车碳排放计算

影响电动车的电能损耗的因素有很多，包括电动车行驶的速度和距离、路况以及自身重量等。其中，车速的动态变化受到空气阻力和道路拥堵等的影响，进而影响电量的消耗；电动车的重量包括空车重量和载重，载重随着对客户点的配送而不断减少。根据已有研究［3］，电动车在弧(i，j)的电能消耗计算如下:

其中:aij=a+gsinθij+gCrcosθij为与路段有关的常数，a表示加速度，g为重力常数，θij为路段角度，Cr为滚动阻力系数；w为电动车空车的重量；γ=0.5Cd Aρ为与电动车型有关的系数，Cd为牵引系数，A为车辆迎风面积，ρ为空气密度。本文所采用的电动车耗电计算方法能够综合反映电动车速度、载重和行驶距离这些关键要素的影响，使得电动车能耗计算更加精确和符合应用实际。

电动车的碳排放量与电动车在弧(i，j)的耗电量pij和电能排放因子e有关，计算如下:

其中，电能排放因子e为单位电能的二氧化碳排放量。我国还有较多的火力发电，而火力发电将产生大量二氧化碳气体，该因子与所使用的电动车型和发电类型有关，在特定的物流配送中为一常数e，将其设定为e=0.7 kg/kWh［18］。

1.3 BE-FRP数学模型

根据综合多种因素的电动车碳排放计算方法，BE-FRP的数学模型描述如下:

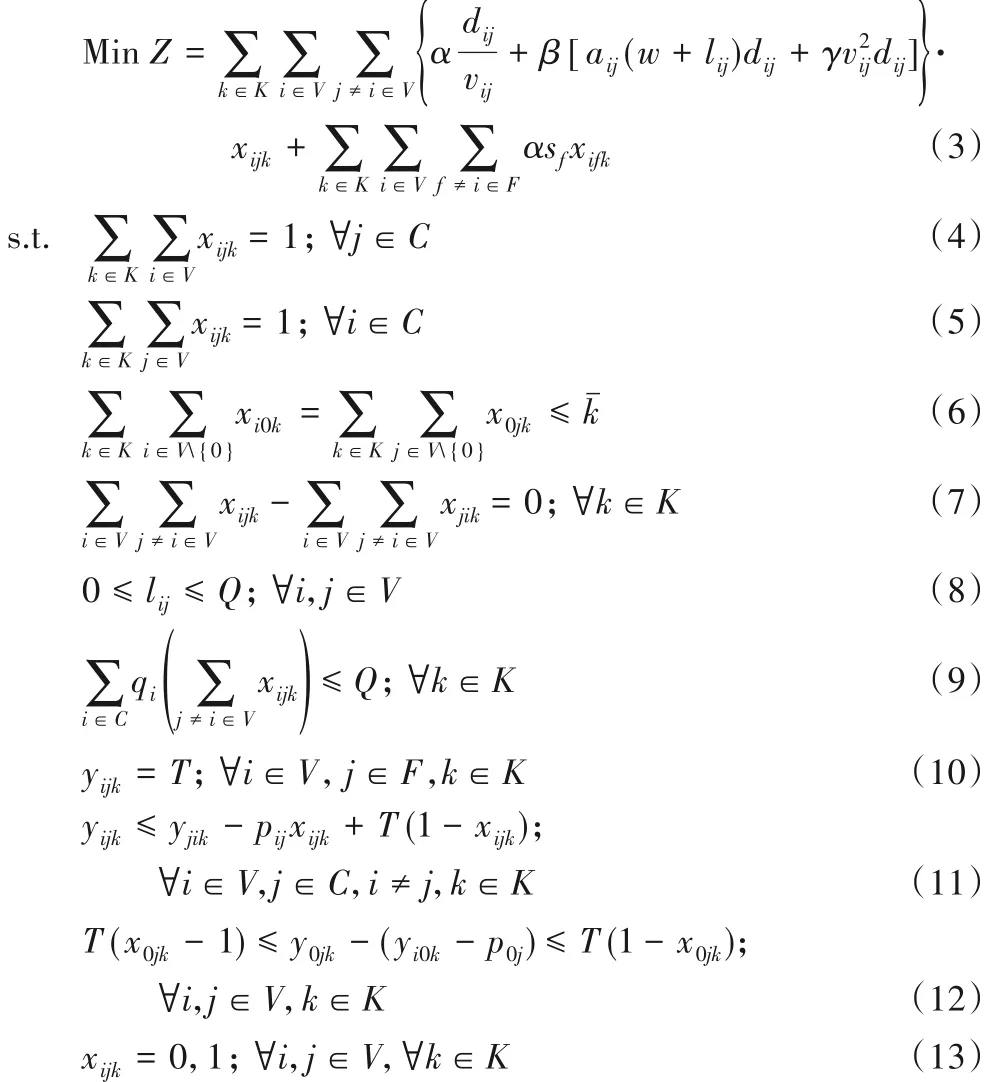
其中:式（3）为目标函数，表示最小化总成本，包括电动车辆使用费用和耗电费用两个部分；式（4）和式（5）为每个客户点的访问唯一性约束；式（6）为配送中心限制，表示所有电动车均在完成配送任务后重新返回出发点配送中心；式（7）保证了每个弧段的流量守恒；式（8）和式（9）为电动车辆的容量约束；式（10）表示电动车在从配送中心或换电站充电后，其电量被充满；式（11）约束了经过客户点后电动车电量消耗程度；式（12）保证了电动车的剩余电量能够确保其完成任务后返回配送中心；式（13）为决策变量的约束。

由BE-FRP 的目标函数可以看出，该问题存在两种特殊的情况，即:1）令α=0，该模型将最小化电动车的耗电费用，根据1.2 节，由于碳排放与电动车的耗电量成正比，也等同于最小化运输中的碳排放；2）令β=0，则模型将以最小化运输中的旅行时间费用为目标，也就是最小化旅行时间。因此，本文模型有利于通过对旅行时间费用和低碳成本的考虑反映出对电动车配送中经济和环境的综合评估。

与传统的VRP 模型相比，BE-FRP 的目标函数考虑了车辆使用和耗电费用构成的总成本，而传统的VRP 往往以总旅行距离最小为目标；同时，BE-FRP 还考虑了与电动车有关的换电站充电约束、电量消耗约束和电动车数量约束，还允许电动车多次访问同一换电站，从而保证了电动车顺利完成配送，也更符合物流配送的实际情况。因此，BE-FRP是对传统VRP的扩展，而经典的VRP则简化成为BE-FRP的一个特例。

2 BE-FRP的求解算法设计

由于经典的VRP 是公认的NP-hard 问题［1］，而BE-FRP 是VRP的扩展，为了提高求解效率，需要设计启发式算法求解该问题，所以本文拟提出一种基于爬山优化和邻域搜索的自适应遗传算法。自适应遗传算法是一种参数能够根据求解过程灵活调节的智能算法［19］，与一般遗传算法相比，其特点是交叉和变异概率随着种群的适应度变化而自适应调整。为了加强算法的局部搜索能力，保证算法快速收敛到最优解，还将引入爬山搜索算法，该算法对当前解采用循环过程，进行优化改进，直到达到“峰顶”时结束。另外，为了满足电池续航能力和换电站约束，对自适应遗传算法得到的最优解中的每条路径进行换电站邻域搜索，进一步改进最优解，最终得到最优可行解。自适应遗传算法的基本流程及各阶段之间的关系如图1所示。

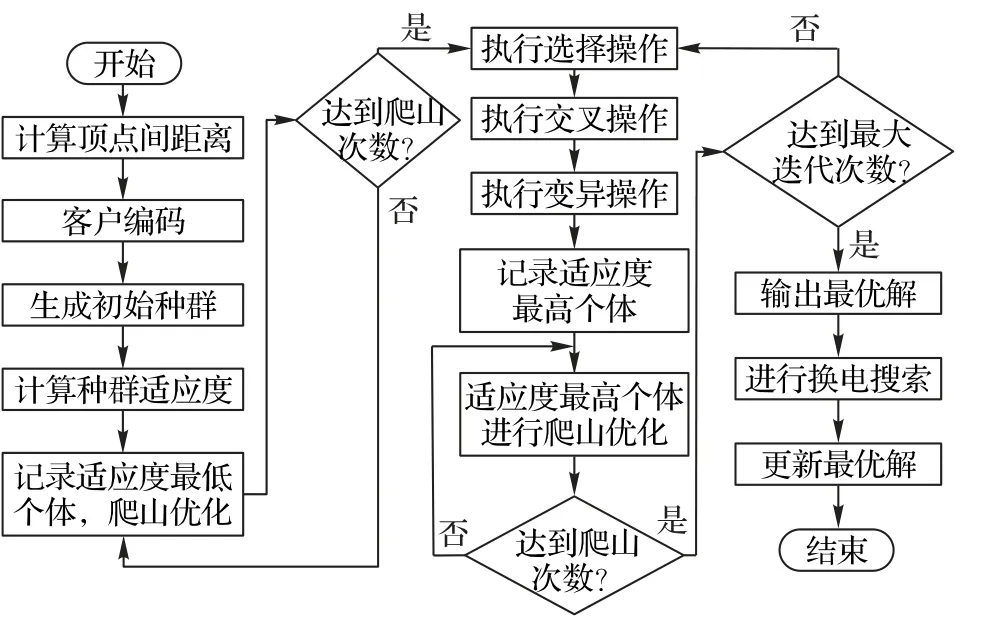
图1 基于爬山优化和邻域搜索的自适应遗传算法Fig.1 Adaptive genetic algorithm based on mountain-climb optimization and neighborhood searching

2.1 算法编码、初始化种群和适应度函数策略

根据BE-FRP 模型特点，选择实数编码策略。首先，根据物流配送中心的数量、客户点数n和换电站数量fˉ设定个体染色体长度；然后在货运路径中加入个体编码元素。自然数编码表示如下:设配送中心为0，客户点为(1，2，…，n)，换电站为(n+1，n+2，…，n+)。由车辆的容量和客户点总需求量可计算出货运中启用的最少电动车数量。

在种群内，个体表示货运路径安排，个体的适应度值一方面取决于个体目标函数值，另一方面取决于是否满足模型规定的约束条件。自然数编码方式在编码时将考虑电动车的总数量、电动货车载重量和续航里程等约束条件。另外由于适应度函数δ追求最大值，这与模型函数最小化总成本Z的目标是相反的，故采用的计算公式为:δ=1/Z。

2.2 选择策略

拟采用的选择策略将融合保留最优个体和轮盘赌法。首先，依次计算出每个个体的适应度值；接着，按照适应度值由大到小对个体进行降序排列，保留适应度值最高的个体进入后续遗传操作；最后，通过轮盘赌法确定剩余个体能否进入后续操作。轮盘赌法将计算个体适应度与群体总适应度的比值，其中Ω为种群中所有个体的集合。个体被选择的概率与该比值成正比。

2.3 交叉策略

交叉策略即对染色体基因进行适当处理，提高解空间的搜索功能，从而产生更优异个体。种群的最小适应度、最大适应度和平均适应度分别用δmin、δmax和表示。设参数μ=(0.5，1)和ν=(0，0.5)。为了说明种群的适应度分布，定义为平均适应度和最大适应度的比值，该值越趋向0.5，表明种群集中程度越高。群体适应度集中程度通过最小和最大适应度的比值来确定，当该比值趋于0 时，表明算法陷入局部最优。另外，若表示为个体适应度集中化的群体，否则表明群体中的个体适应度较为分散。

交叉策略的设置应尽量减少保留表现不好的个体和近亲交叉操作，防止算法过早收敛。定义pc为交叉概率，U为父代个体分量的集合，和代表父代个体的第i个分量，xmin和xmax分别表示个体内的最小和最大分量，δ1和δ2表示父代的两个适应度。根据上述原则，自适应交叉概率［20］可计算如下:

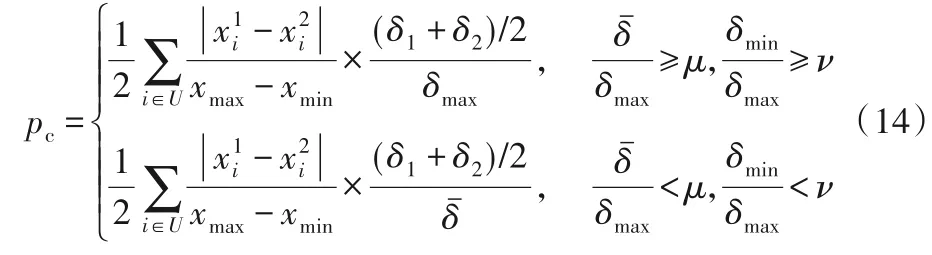
由于算法前期种群内个体一般较为分散，父代个体基因具有较大差异，交叉操作的概率将与个体适应度值成正比。在算法执行后期，种群个体表现得较为集中，交叉操作有两种可能:1）父代个体间基因表现为差别较小，算法可能趋向最优解，那么需要提高交叉操作的概率使得平均适应度能够进一步接近最大值。2）父代个体间基因表现相差较大，容易导致局部最优解，那么就需要使用更大的交叉概率。

通过判断交叉概率pc与(0，1)内产生的随机实数的大小关系决定是否启用交叉策略。只有pc大于该随机数值时才执行如下的交叉操作:1）任意选择两条染色体作为交叉操作的父代染色体。2）对给定的父代染色体中的两条车辆路径，随机选择交叉位置，执行次序交叉操作。3）将交叉后的两条车辆路径的子染色体合并，删除连续为0 的元素，从而产生两条新染色体。

2.4 变异操作策略

变异操作模仿基因遗传中的染色体突变，从而增加解空间中种群和染色体的多样性。利用自适应的变异概率，这样可以增强个体的多样性，使算法尽快跳出局部最优的搜索过程。自适应的变异概率计算如下:

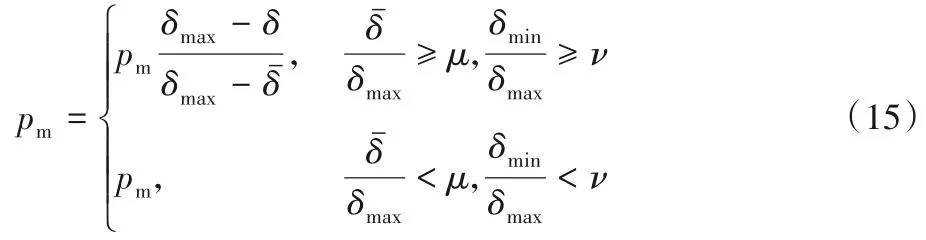
算法在前期时拟采用常数的变异概率，这是由于前期个体分散程度较高，种群具有较大的多样性。而算法到了后期，解空间的个体集中性和种群多样性都比较低，则根据适应度来自适应调整变异概率。如果个体适应度小于其平均值，那么适应度值减少，变异概率将增加；否则，变异概率将随着个体适应度的增加而减小。

首先通过计算自适应交叉概率pm与(0，1)内随机实数的大小关系判断个体是否需要执行变异操作。如果pm比该值小，则不执行变异过程；否则，开展如下变异操作过程:1）将选定的染色体当成父代染色体。2）在父代染色体中，对所有车辆路径随机确定变异位置，并进行交换变异操作。3）删除连续为0 的元素，合并车辆路径的子染色体，从而形成新染色体。

2.5 爬山优化与终止准则

爬山优化将应用于算法过程的以下两个部分:1）优化产生的初始种群并改进种群的个体适应度。2）在算法遗传过程执行后，优化最优适应度个体，实现对遗传操作最优解进行局部寻优，尝试进一步改进该解。

爬山优化将执行如下步骤:

步骤1 对染色体表示的子车辆路径，随机选择基因所在位置，并执行互换的操作。

步骤2 对比互换操作前后每个个体适应度发生的变化，若个体适应度值减少或不变，则原染色体也不变；否则，进行原染色体更新操作。

步骤3 判断是否到达终止条件，如果没有到达则循环执行步骤1和步骤2。

对于算法终止规则的设定，常见的有三类:1）达到预先给定的目标函数值，则算法终止，该方法通常需要预先知道最优目标值，然后对其进行反证。2）算法连续执行设定的若干次数没有改进当前解，则算法终止，由于连续执行的次数难以预先估计，导致算法可能无法跳出局部最优解。3）可以根据要求的计算时间和精度，设定算法的最大迭代次数，最终保证算法收敛到最优解，故本文研究选择该终止规则。

2.6 邻域搜索策略

电动车换电站点的邻域搜索就是根据客户点与换电站的位置，确保最优解中的每条路径都满足电动车的续航能力约束和换电站约束。假设换电站的位置是给定的，电动车在按照配送顺序行驶到某一客户点时，根据其剩余电量能否到达下一客户点决定是否进行换电操作，如果它的剩余电量不足以行驶到下一客户点，根据这两个客户点之间的行驶半径寻找最近的换电站位置，换电站邻域搜索的主要流程如图2所示。

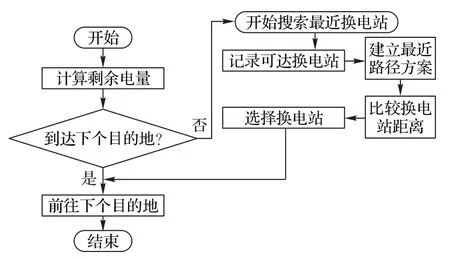
图2 电动车换电站邻域搜索Fig.2 Battery-swapping neighborhood searching for electric vehicle

邻域搜索具体过程如下:

步骤1 在货运路径中，当电动车访问某一客户点时，对货运电动车的当前可用电量进行计算。

步骤2 根据可用电量估算电动车能否正常到达下一目的节点（可能是客户点或配送中心）。如果能够到达，则转到步骤3；否则，转到步骤4。

步骤3 继续前往下一节点，直至所有节点搜索完毕终止。

步骤4 按照邻域规则记录下就近的换电站及其数量。

步骤5 对于每个候选的换电站，确定该电动车通过该换电站进行充电服务的行驶距离。

步骤6 对通过每个换电站的行驶距离进行比较，根据邻域原则确定最优方案。

步骤7 该节点的换电站邻域搜索终止，转到步骤3。

2.7 自适应遗传算法具体执行步骤

通过上述对算法关键内容的详细分析，自适应遗传算法的具体执行安排如下:

步骤1 初始化。初始种群规模设定为Inn，算法最大迭代次数为Gnmax，确定网络图中任意两节点间的行驶距离。对个体进行自然数编码，初始化满足模型约束条件的种群。计算出每个个体的适应度值，并选择出适应度最小的个体。

步骤2 执行爬山优化操作，改进适应度最小的个体，并设定初始爬山次数为t=0。

步骤3 根据总爬山次数Tmax确定是否终止爬山操作。如果达到，则替换种群当前解为最优解；否则，转到步骤2，并更新t=t+1。

步骤4 确定选择概率为(0，1)的随机数，按照适应度水平对种群中的个体排序，若个体适应度不是最高的，则根据轮盘赌法设定选择概率，如果个体适应度达到了最高，其选择概率可设定为1。初始化执行次数s=0。

步骤5 交叉策略。产生(0，1)的随机实数，若交叉概率小于该值，不进行交叉；否则执行交叉操作。

步骤6 变异策略。产生(0，1)的随机实数，若变异概率小于该值，则不进行变异；否则执行变异操作。

步骤7 对新的种群，计算各个体的适应度值并给出适应度最大的个体。初始化爬山次数b=0。

步骤8 利用爬山搜索优化适应度最高的个体，一旦适应度增加则更新最优解。

步骤9 爬山次数是否达到最大执行数目Bmax，一旦达到则更新最优解；否则，令b=b+1并执行步骤8。

步骤10 算法终止条件。执行次数是否达到Gnmax，如果达到最大迭代次数，则对当前的最优个体进行记录，转到步骤11；否则转到步骤5，并更新迭代次数s=s+1。

步骤11 利用换电站的邻域搜索方法对遗传算法得到的最优解进行后优化，记录下最优可行解。

步骤12 终止整个算法，输出最优可行解。

3 实验与结果分析

3.1 实验设置

某所在地区货运公司从其一配送中心出发为客户执行送货服务，假设该中心有5 辆电动车。选取该公司29 个订单的数据，包括:客户点的位置、需求量和换电站（5 座）。电动车离开配送中心或在换电站充电后假设电池被充满，换电时间为0.1 h，电动车货运的平均速度为60 km/h。目前微面和轻卡是电动车市场的主力，考虑到市场实际和经济效益，货运电动车选择电动车中微面型的“电牛一号”，并将其参数作为仿真数据。另外，将工业用电的价格0.8 元/kWh 作为电动车换电的可变费用。

结合实际情况和电动车相关参数，实验仿真中的模型相关参数设置如下:电动车使用成本α=120元/h；充电费用β=0.8 元/kWh；电池容 量T=35.7 kWh/L；换电服 务时间sf=0.1h；空车重量w=1325 kg；车辆最大载重Q=595 kg；加速度a=0 m/s2（假设匀速行驶）；重力常数g=9.81 m/s2；路段角度θij=0；滚动阻力系数Cr=0.01；牵引系数Cd=0.7；车辆迎风面积A=0.378 m2；空气密度ρ=1.204 1 kg/m3。

3.2 算法参数设置与分析

参数设置直接影响算法的收敛性，主要从初始种群的大小、自适应交叉、变异概率和爬山搜索次数多个方面设置最优的参数范围，加快算法收敛速度。首先确定合适的种群规模，为此依次对［50，310］区间中每次增加20 的种群规模进行测试，每组种群进行10次运算，图3给出了算法的平均收敛代数和收敛概率。由图3 可以看出，随着种群规模的增加，平均收敛代数总体先减少后增加，而收敛概率则正好相反，即种群规模太大或太少都会减小收敛概率。特别地，当种群规模达到210 时，具有最大的收敛概率，同时只需要最少的迭代次数就可以收敛。为此，将初始种群规模的参数选为210 时最为合适。

图3 最佳种群规模的设置Fig.3 Setting of optimal population size

下面对自适应与常数的交叉和变异概率进行比较。使用确定的最优种群规模210，算法在迭代到200 次时终止，常数时的交叉和变异概率分别为0.8 和0.06。图4～5 为仿真50 次获得相同最优解时常数概率和自适应概率的收敛情况。可以看出，常数概率的方案在算法初期表现较好，但当迭代50 次以后，自适应概率的方法通过提升交叉概率，保证算法较快接近最优解。当迭代次数超过160 后，自适应方法增加了变异概率，使得算法更快达到最优解。总之，通过交叉和变异概率参数的自适应调整，有利于算法快速全局寻优，提高了算法的灵活性。

图4 交叉和变异概率为常数下的收敛曲线Fig.4 Convergence curves with fixed crossover and mutation probabilities

下面通过数值实验探讨如何设置最优的爬山搜索迭代次数。给定前文实验得到的最佳初始种群规模和自适应的交叉、变异概率，在区间［0，210］选取爬山搜索次数，每个候选次数运行10 次求算法的平均适应度和平均收敛代数，结果如图6 所示。可以看出，平均适应度和平均收敛代数随着爬山次数的变化波动较大，总体上当爬山次数位于［25，40］，算法收敛快且平均适应度也比较高。故为了加快算法的收敛，将爬山次数设定在35次。

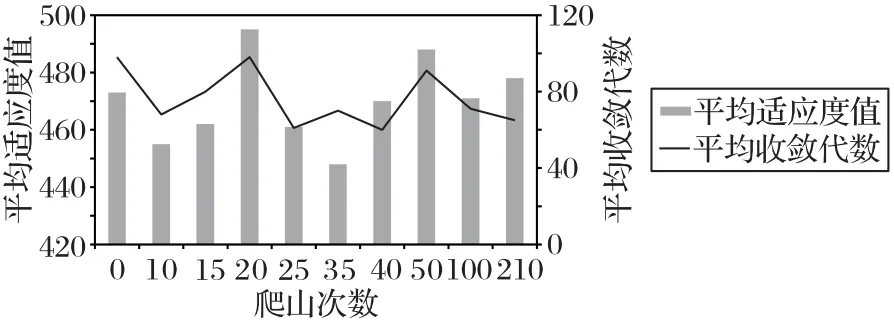
图6 爬山次数的设定Fig.6 Setting of mountain-climb number

3.3 模型计算结果分析

选用Matlab 7 对自适应遗传算法进行编程实现，求出数值案例的最优解。限制电动车为3 辆，根据前面的初步参数实验，拟设置参数为:算法最大迭代次数350，爬山最大次数35，初始种群规模210。运行算法20 次，记录前5 个最佳路径结果，如图7 所示。由图7 可见，最优路径为线路5，且如图8所示，共三条子路线，其总费用为277.68 元，碳排放总量为93.5 kg。通过对比可得，该最优解在所有可行解中不仅实现了总成本的最小化，也最大限度地降低了碳排放量。

图7 模型求解路径结果Fig.7 Result of model solving routes

图8 换电式电动车配送最优路径Fig.8 Optimal distribution route of battery-swapping electric vehicle

3.4 算法比较分析

为了说明所提出的改进的自适应遗传算法的求解表现，将其与基本的常数参数的遗传算法进行比较。终止规则是评价各算法以何种收敛速度达到当前最优解的适应度值。如果达到最优适应度值，则判定为收敛；否则算法不收敛。同样选取初始种群数量为210，基本遗传算法（概率固定）中变异概率为0.05，交叉概率为0.8。图9 给出了两种算法分别运算10次的结果。从图9 中可以看出，自适应遗传算法迭代次数在50～100，相较于传统的遗传算法，平均减少了52.1%，这表明所提出的自适应遗传算法具有更高的求解效率，能够更快地收敛到最优解。

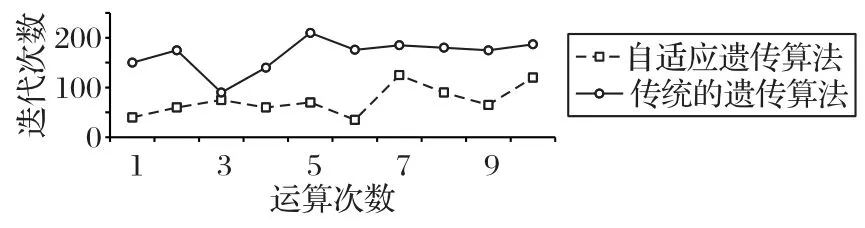
图9 不同算法迭代次数比较Fig.9 Comparison of iteration times of different algorithms

4 结语

绿色环保已成为世界主题，发展电动汽车是我国能源战略转型和未来汽车行业发展的方向。研究和分析基于电动车的物流运输具有十分重要的现实意义，优化电动车货运路径是实现物流配送节能减排的重要举措。本文以经典的VRP作为基本参考模型，引入了综合考虑速度、载重和行驶距离等多种因素的电动车能耗与碳排放计算方法，并考虑了电动车的容量、电池续航能力和换电站多次服务等新的约束，建立了考虑电动车使用费用和耗电费用的换电式电动车货运路径优化问题模型——BE-FRP。算法比较结果表明，所提出的自适应遗传算法能够更快地收敛到最优解，提升了算法的效率。

本文研究将为采用电动车作为运输工具的物流企业的实际配送操作提供优化模型和求解算法等决策支持，同时也可为政府制定电动车物流政策提供参考。