基于带梯度惩罚深度卷积生成对抗网络的页岩三维数字岩心重构方法

王先武，张 挺*，吉 欣，杜 奕

（1.上海电力大学计算机科学与技术学院，上海 200090；2.上海第二工业大学工学部，上海 201209）

（∗通信作者电子邮箱tingzh@shiep.edu.com）

0 引言

油气资源作为一种不可再生资源，是国民经济发展的重要物质基础。面对常规油气资源需求快速增长的压力，非常规油气的勘探与开发逐渐受到人们的重视。页岩油气是典型的非常规油气，具有源储一体、分布广泛、资源潜力大等优点。页岩具有低孔隙度、低渗透率和各项异性等特点，导致页岩油气的勘探和开采非常困难。页岩的一些宏观特性（如孔隙度、渗透率等）取决于它的微观结构，开采页岩油气必须要了解掌握页岩的微观内部结构［1-2］。

三维数字岩心重构技术是了解掌握页岩微观结构的重要手段。三维数字岩心本质上是岩心结构的三维数字化图像，通常离散为三维矩阵形式，三维数字岩心的每个体素点对应矩阵中单个元素。近年来，研究三维数字岩心重构的方法大致可分为:物理实验方法、传统数值重构方法和机器学习数值重构方法。

常用的物理实验方法有扫描电子显微镜（Scanning Electron Microscope，SEM）、聚焦离子束扫描电子显微镜（Focused Ion Beam Scanning Electron Microscope，FIB-SEM）和电脑断层扫描（Computer Tomography，CT）等。扫描电子显微镜主要提供二维图像，适用于二维数字岩心的重构。FIBSEM 可对亚微米级样品进行实时成像，但无法完成岩石中纳米尺度的孔隙成像。CT 扫描法利用灵敏度极高的探测器对岩石进行断层扫描，借助计算机直接得到三维数字岩心图像。上述方法具有速度快、图像清晰等特点，但由于设备昂贵和实验成本高，很难得到广泛应用［2］。

传统数值重构方法以易于获取的二维岩石图像为基础，以二维孔隙形态特征的统计信息作为约束条件，利用数值模拟来完成页岩的三维数字岩心重构。早期出现的模拟退火法［3］、过程法［4］和顺序指示模拟法［5］利用低阶统计信息完成数字岩心三维重构，但重构孔隙的连通性存在缺陷。之后出现的多点统计法（Multiple Point Statistics，MPS）［6］利用高阶的统计信息重构数字岩心，侧重于表达孔隙结构多点之间的相关性。近年来，在MPS 的基础上，出现了单一标准方程模拟（Single Normal Equation SIMulation，SNESIM）［7］、滤器模 拟（FILTER SIMulation，FILTERSIM）［8］、直接采 样（Direct Sampling）法［9］等改进方法。SNESIM 利用搜索树保存训练图像的概率信息。FILTERSIM 利用一套过滤器将各个模式分类，然后对待模拟区域进行模拟。直接采样法通过使用自定义的数据模板扫描训练图像，获取待模拟节点的状态值。但这些方法依然存在着重构时间较长的问题。

随着机器学习尤其是深度学习的高速发展，许多数据重构问题都在其中找到解决方案。深度学习是机器学习的一种实现方式，得益于其强大的特征提取能力，可利用训练图像的结构特征进行重构，并产生了若干分支算法，例如深度迁移学习（Deep Transfer Learning，DTL）［10］、卷积神 经网络（Convolutional Neural Network，CNN）［11］和生成 对抗网 络（Generative Adversarial Network，GAN）［12］。

GAN 中包含鉴别器和生成器，其特点在于通过内部鉴别器与生成器的对抗，隐式总结出数据集的数据特征，最终通过生成器将总结出的数据特征以目标数据形式反馈给用户。鉴别器期望准确地区分生成图像和训练图像，而生成器的目标在于生成可以欺骗鉴别器的高质量图像。完成指定的训练次数后，GAN 可以提取出训练图像的整体特征，并利用生成器生成以假乱真的图像以达到图像重构的目的。GAN 的缺点在于训练的稳定性差，很容易发生梯度消失和梯度爆炸。深度卷积生成对抗神经网络（Deep Convolutional Generative Adversarial Network，DCGAN）［13］、WGAN（Wassertein GAN）［14］是GAN的变体，它们在GAN的基础上改变网络结构和设计新的损失函数，让网络生成样本质量更高，训练过程更加稳定。基于DCGAN，本文提出了一种带有梯度惩罚［15］深度卷积生成对抗网络（Deep Convolutional Generation Adversarial Network with Gradient Penalty，DCGAN-GP）方法，用于页岩三维数字岩心重构。相较于DCGAN，新加的梯度惩罚项会使带梯度惩罚深度卷积生成对抗网络（DCGAN-GP）整体训练更稳定，收敛速度和训练速度更快。实验结果表明，与其他一些重构方法相比，DCGAN-GP重构结果更接近训练图像，而且重构速度具有明显优势。

1 本文方法

1.1 GAN

GAN［12］包含两个多层感知机模型:鉴别器D和生成器G。生成器将随机噪声z映射到图像空间得到生成图像G(z)。z通常由符合正态分布Pz的独立实数组成，代表生成器的随机输入。鉴别器用来计算随机样本来自“真实”数据的概率。鉴别器期望正确标记每个样本，而生成器专注于“欺骗”鉴别器，使鉴别器误判生成图像G(z)为真实数据。GAN 结构如图1所示。

图1 GAN的结构Fig.1 Structure of GAN

鉴别器根据输出结果得到GAN 的损失。通常情况下把最小化GAN的损失函数当作最小化-最大化问题，如下所示:

1.2 本文方法DCGAN-GP

虽然GAN 可以重构图像，但是训练过程不稳定，有时可能会产生难以预料的结果。Sagawa 等［13］提出了一种将CNN和GAN 结合的DCGAN 方法用于面部图像重构。DCGAN 的生成器和鉴别器能够学习训练图像的组成结构，其总结出的数据集合中的数据和特征的关系具有很强的泛化能力。

由于DCGAN 继续沿用了GAN 的损失函数，这样在训练过程中需要仔细平衡生成器和鉴别器的优化，否则会导致训练不稳定甚至梯度爆炸。因此本文基于DCGAN 提出了一种改进的带有梯度惩罚的DCGAN-GP方法，该方法沿用DCGAN的生成器与鉴别器的结构，舍弃了GAN 原有的损失函数，为鉴别器损失函数添加额外的梯度惩罚。DCGAN-GP鉴别器和生成器的主要结构如图2所示。

图2 DCGAN鉴别器与生成器内部结构Fig.2 Internal structures of discriminator and generator of DCGAN

图2 中，三维卷积（3D Convolution，Conv3d）和三维转置卷积（3D Transposed Convolution，ConvTranspose3d）分别是基于CNN 修改之后的跨步卷积（strided convolutions）和分数跨步卷积（fractional-strided convolutions）操作，可以有效地提高训练的稳定性。BatchNorm3d 是加速训练和减缓训练过拟合的重要操作［17］。图2内的鉴别器重复两次执行Conv3d和激活函数LeakyReLU［18］的组合，最后输出结果。生成器共执行三次ConvTranspose3d，前两次ConvTranspose3d 后都会经过BatchNorm3d 和激活函数ReLU［19］处 理。最后一 次执行ConvTranspose3d后，通过激活函数Tanh处理后输出结果。

DCGAN-GP利用额外的梯度惩罚来解决训练中梯度消失和梯度爆炸的问题。首先分别在真实样本空间Pr和生成样本空间Pg中获取样本xr和xg，然后在真实样本xr和生成样本xg之间随机插值得到，如式（2）、（3）所示:

其中:U[0，1]表示[0，1]上相同间隔的分布概率是等可能的。鉴别器的原始损失函数如式（4）所示:

其中:∇xD(x)表示鉴别器的输出值在x方向上的梯度；表示鉴别器的输入为随机插值采样时的数学期望。DCGANGP的鉴别器损失函数如式（6）所示:

2 重构页岩方法的流程

本文方法基于Tensorflow-GPU 框架进行页岩数字岩心的重构［20］。借助该框架的优势，本文方法可以充分利用图形处理单元（Graphics Processing Unit，GPU）实现数字岩心的重构，但是用户不必在使用框架时为GPU 专门设置任务分配和整合重构结果，因此使整个重构过程相对简化。首先，对页岩训练图像进行去噪、二值化等预处理；其次，设计网络结构、设置超参数并完成网络参数初始化；再次，设定目标训练次数开始训练，训练过程中利用梯度下降反向更新网络参数；最后，保存网络参数，生成器重构出页岩三维数字岩心。图3 所示是利用DCGAN-GP重构页岩三维数字岩心的流程。

图3 基于DCGAN-GP重构页岩数字岩心的流程Fig.3 Flow chart of reconstructing digital core of shale based on DCGAN-GP

3 实验与结果分析

3.1 超参数的选择

模型中超参数的选择主要根据文献［15］所推荐的经验参数，生成器训练5次进行1次参数更新，鉴别器训练1次进行1次参数更新。鉴别器和生成器的优化器都设定Adam 学习率α=1.0×10-4。

3.2 实验数据

首先利用纳米CT 获取页岩的体数据，分辨率为64 nm/voxel。从上述页岩体数据截取出尺寸为64×64×64体素的页岩数据作为三维训练图像（孔隙度=0.154）。该三维训练图像也可以视为64 幅二维图像（每幅64×64 像素）依次叠加而成。图4（a）表示整个训练图像的外表面，图中黑色表示页岩的孔隙，灰色表示页岩的骨架。图4（b）所示为页岩训练图像的正交剖面（X=32，Y=32，Z=32）。图4（c）为页岩训练图像的孔隙结构。

图4 页岩训练图像的结构Fig.4 Structure of the shale training image

3.3 重构结果对比

将三维训练图像转化为三维数组用于本文方法中神经网络的训练。训练完成后，生成器利用保存的参数直接生成重构的页岩三维数字岩心（尺寸为64×64×64 体素）。同时，利用经典的重构方法FILTERSIM、SNESIM、Direct Sampling 和原始的DCGAN 进行页岩数字岩心的重构，将重构结果与DCGAN-GP重构结果进行对比。

3.3.1 页岩重构结果比较

图5～9 分别是 使用了FILTERSIM、SNESIM、Direct Sampling、DCGAN 和DCGAN-GP 方法重构的页岩三维数字岩心。可以看出，上述五种方法重构的页岩数据都与真实的页岩训练图像有着相似的孔隙分布特征和长连通性孔隙结构，但是其中FILTERSIM 重构数据的孔隙大小和分布与训练图像差异较大，其他四种方法重构数据在孔隙大小和分布方面更接近训练图像。然而仅凭观察图5～9重构结果难以较好判断重构质量，因此下面将对重构结果作进一步对比分析。

图5 FILTERSIM方法的页岩重构结果Fig.5 Shale reconstruction results of FILTERSIM method

图6 SNESIM方法的页岩重构结果Fig.6 Shale reconstruction results of SNESIM method

图7 Direct Sampling方法的页岩重构结果Fig.7 Shale reconstruction results of Direct Sampling method

图8 DCGAN方法的页岩重构结果Fig.8 Shale reconstruction results of DCGAN method

图9 DCGAN-GP方法的页岩重构结果Fig.9 Shale reconstruction results of DCGAN-GP method

3.3.2 重构结果孔隙度对比

页岩孔隙度用来表示页岩存储流体的能力，是评价页岩重构结果的重要指标之一。页岩孔隙度φ的定义如下:

其中:Vp为页岩孔隙体积；V为页岩体积。为了避免重构结果的偶然性，分别利用FILTERSIM、SNESIM、Direct Sampling、DCGAN 和DCGAN-GP 方法重构10 次页岩数字岩心。表1 所示为不同方法10 次重构结果的孔隙度。由表1 可以看出，与训练图像的孔隙度（0.154）相比，DCGAN-GP重构结果的平均孔隙度更接近，表明所提方法重构质量最好。

表1 不同方法10次重构数字岩心的孔隙度Tab.1 Porosity of digital core reconstructed by different methods for 10 times

3.3.3 重构结果变差函数对比

变差函数被广泛地用于空间数据结构特征的相似性评价［21］，其定义如下:

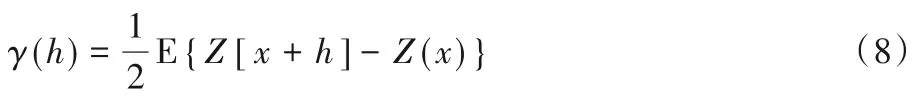
其中:E 是数学期望值；h是x位置和x+h之间的滞后距离；Z（x）是位置x处的属性值。变差函数主要反映一定方向上的空间两点变量之间的相关性和变异性，如果重构结果的变差函数曲线与训练图像的曲线越贴合，那么重构结果与训练图像的特征相似度越高；否则说明差异较大。

将FILTERSIM、SNESIM、Direct Sampling、DCGAN 和DCGAN-GP 方法的重构结果与训练图像的变差函数进行对比。图10（a）、（b）、（c）分别展示了各重构方法在X、Y、Z方向上的变差函数曲线，可以看出DCGAN-GP 与训练图像的变差函数最为相似。

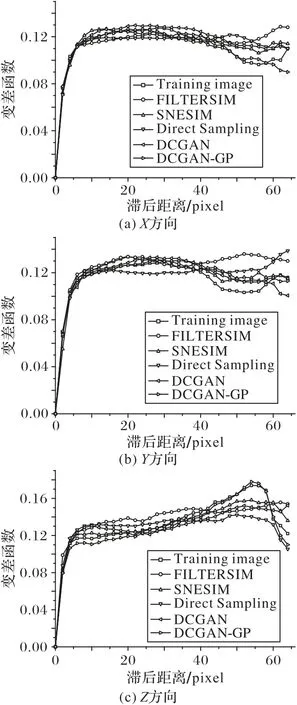
图10 页岩重构结果的变差函数对比Fig.10 Comparison of variograms of shale reconstruction results

3.3.4 重构结果孔隙数量和分布对比

对FILTERSIM、SNESIM、Direct Sampling、DCGAN 和DCGAN-GP 方法的重构结果进行孔隙数量、孔隙尺寸和孔隙尺寸分布分析。表2所示为训练图像和各重构方法10次重构结果的平均孔隙数量。表3给出了训练图像和各重构方法10次重构结果的孔隙最大值、最小值以及平均孔隙直径。图11所示为训练图像和各重构方法10 次重构结果的平均孔隙直径分布。

表3 训练图像和各重构方法10次重构结果的孔隙直径的平均值、最小值和最大值 单位：voxelTab.3 Mean values，minimum values and maximum values of pore diameters of training images and 10 times reconstruction results of different reconstruction methods unit:voxel

结合表2～3 和图11 可以看出，除了在平均孔隙上表现稍差之外，DCGAN-GP 重构结果在孔隙数量、孔隙最大直径、孔隙最小直径和直径分布上与训练图像最为相似。

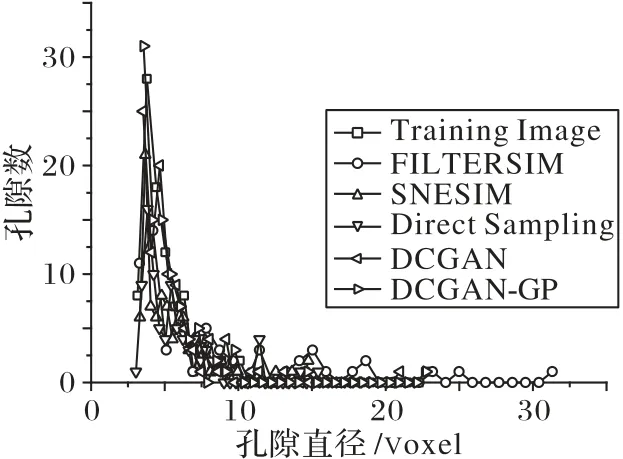
图11 孔隙直径分布对比Fig.11 Comparison of pore diameter distribution

表2 训练图像和各重构方法10次重构结果的平均孔隙数Tab.2 Average pore number of training image and 10 times reconstruction results of different reconstruction methods

3.3.5 CPU、GPU和内存使用率对比

本文采用的硬件实验环境为:Inter Core i7-9700k 4.1 GHz CPU，16 GB 内存，GeForce RTX2070s GPU（8 GB 显存）。表4 所示是FILTERSIM、SNESIM、Direct Sampling、DCGAN 和DCGAN-GP 方法重构10 次页岩数字岩心时的CPU与GPU使用情况和内存的平均使用量。

从表4 可以看出，三种经典重构方法对CPU 和内存的占用比较高，而DCGAN-GP 和DCGAN 的CPU 和内存使用量相较于另三种方法要低很多。出现上述情况的原因在于DCGAN-GP 和DCGAN 可以通过Tensorflow-GPU 框架把大量计算交给擅长浮点运算的GPU 处理，加速了网络的训练过程。

表4 把总重构时间分为两部分:“第一次重构时间”和“其他9 次重构时间”。“第一次重构时间”指五种方法完成一次重构所消耗的时间，“其他9次重构时间”是五种方法完成9次重构所消耗的时间。由于计算机在运行算法时空间分配的随机性，所以每次重构时间会存在少许的不同。DCGAN-GP 和DCGAN 第一次重构过程中需要完成网络的训练，这个训练过程花费时间较多，而其他三种经典方法第一次重构过程中的训练速度相对较快。虽然DCGAN-GP 和DCGAN 在第一次重构时的训练过程需要大量的训练时间，但随后的每次重构所消耗的时间较少，这是因为DCGAN-GP 和DCGAN 能够将第一次训练完成后得到的参数保存到文件，后继的每次重构只需要读取文件内的参数就可快速完成图像重构。与此不同的是，另外三种经典重构方法每次将训练信息保存在内存中，重构一旦结束，所有训练图像的特征信息将被清除，因此它们每次重构都要重新扫描训练图像以进行重新训练，这样的重复训练会消耗大量时间。即使对经典重构方法进行改造，未来将这些特征信息也保存在文件中重用，但由于这些方法产生的图像特征的结构信息非常庞杂，仍然会导致重构速度难以大幅提升。因此，当重构多个数字岩心结果时，DCGAN-GP在重构速度和CPU 使用率方面优于其他典型的重构方法和DCGAN，在页岩三维数字岩心重构方面具有优势。

表4 各方法占用内存峰值，CPU、GPU使用量和重构时间对比Tab.4 Peak memory usage，CPU and GPU usage and reconstruction time comparison of different methods

3.3.6 DCGAN-GP的学习率和训练次数

前文提到，DCGAN-GP使用了较多的超参数，大多数超参数可以设置为经验值，其中学习率和训练次数是非常重要的两个超参数，因此针对学习率和训练次数进行对比实验，说明选择这两个超参数的操作过程。实验中使用相同的页岩训练图像，除学习率和训练次数之外的所有参数不变。实验中分别选用3 个不同的学习率:2×10-4、1×10-4、1×10-5。为了方便观察损失曲线变化，对鉴别器的损失值进行取负操作。图12 中黑色部分描绘了鉴别器的损失变化范围。为了便于观察损失值的变化趋势，对损失函数做移动平均平滑处理［22］得到图中灰色部分。灰色部分可以视为原始损失曲线的平均值。从图12 中可以看出，重构结果a、d 的孔隙结构特征与训练图像差异较大，重构结果c 的孔隙度（0.056）要远低于训练图像孔隙度。当学习率取1×10-4，训练40 000次时重构结果b 的孔隙度（0.156）与训练图像更接近，同时鉴别器损失值也更接近于0，说明鉴别器对输入图像判断得更准确，重构结果更接近训练图像。

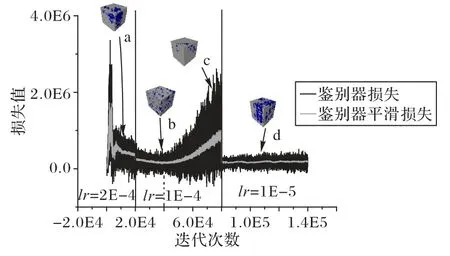
图12 三种不同学习率下鉴别器损失对比Fig.12 Loss comparison of discriminator under three different learning rates

3.3.7 DCGAN-GP与DCGAN的损失对比

与DCGAN 相比，DCGAN-GP主要对鉴别器的损失函数进行了修改，而两者的生成器损失函数完全一致，因此通过比较两者的鉴别器损失来衡量两种方法的性能优劣。图13 展示了DCGAN-GP 与DCGAN 鉴别器损失对比，两种方法的损失曲线有着明显区别。其中DCGAN-GP 的损失曲线在图中波动较小，在68 000次训练前损失曲线处于图像下方，在68 000次训练之后处于图像上方。而DCGAN 损失曲线在图中波动较大，在68 000次训练前损失曲线处于图像上方，在68 000次训练后整体处于图像下方。由于两者采取的损失函数不同，所以图13中值域的大小不同，但DCGAN-GP 损失变化波动相对较小，而且训练16 000 次到训练40 000 次之间有明显的梯度下降，所以DCGAN-GP 可以快速确定最优训练参数，并且训练速度也快于DCGAN。因此，DCGAN-GP 相比DCGAN 更快速和稳定。

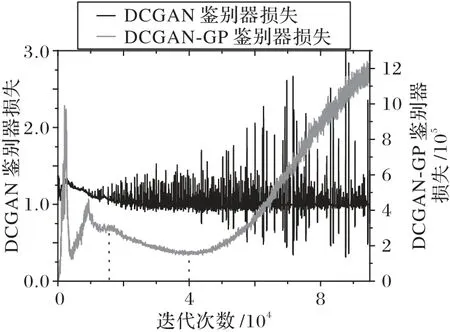
图13 DCGAN-GP与DCGAN的损失对比Fig.13 Loss comparison between DCGAN-GP and DCGAN

4 结语

页岩内部结构复杂，且具有低孔隙度和低渗透率等特点，这将会给页岩油气开采带来巨大挑战。构建页岩的三维数字岩心，可以从微观结构分析页岩宏观特性，提高页岩油气勘探和开采效率。传统数值重构技术每次重构时均要扫描训练图像以提取岩石内部的结构信息，然后利用上述信息重构数字岩心，因此传统数值重构技术的统计信息越高阶，其对硬件要求就越高，消耗时间也就越多。最近出现的机器学习数值重构方法，利用网络隐式提取岩石的特征，可在深度学习（如Tensorflow-GPU）框架的帮助下，利用GPU 加速完成网络训练，重构效率较高。

本文提出了一种基于DCGAN-GP 的三维页岩重构技术，继承了机器学习数值重构方法重构效率高的优势，并且利用带有梯度惩罚的损失函数加快网络收敛，使整个训练过程更稳定。实验结果表明DCGAN-GP 在孔隙度、变差函数曲线、孔隙分布等方面都优于经典数值重构方法。DCGAN-GP一次训练、多次运行的优点有助于提高重构页岩数字岩心的效率。