基于顶点冲突学习的最大公共子图算法

王 宇，刘燕丽，2*，陈劭武

（1.武汉科技大学理学院，武汉 430081；2.冶金工业过程系统科学湖北省重点实验室（武汉科技大学），武汉 430081）

（∗通信作者电子邮箱yanlil2008@163.com）

0 引言

图被广泛应用于描述事物的结构或事物之间的复杂关系，如互联网、社交网络、蛋白质交互网络、化学分子结构、电力网、公路网、图像处理中的属性图等［1］。给定模式图和目标图，子图同构问题是判断在目标图中是否存在与模式图完全同构的子图。最大公共子图（Maximum Common induced Subgraph，MCS）问题是子图同构问题的优化形式，即在模式图和目标图中找到满足同构条件的最大子图。

图匹配问题广泛应用于图像处理［2-3］、生物化学［4］、信息检索［5］、模式识别［6］、社交网络［7］等领域。图匹配问题可以识别数据集成中元数据或模型的对应关系。在生物学和生物化学领域，基因序列中每个基因可以表示为图的顶点，若染色体上两个基因相邻，则图中对应的顶点之间存在边。利用图匹配可以发现基因组中是否含有相同的基因。在模式识别中，图匹配可以提取多个图像中相似的对象。在Facebook等社交网络中，顶点表示每个用户，有向边表示用户之间的好友关系。利用已有的社交关系，为用户推荐好友，也是图匹配问题的应用之一。

文献［8］提出了基于约束规划（Constraint Programming，CP）模型的树搜索算法。对于给定的模式图P和目标图T，每次选择一个〈v，w〉（v∈VP，w∈VT）顶点匹配对作为空间搜索树的分支点；界函数计算子树含有的顶点的最大待匹配对个数，作为剪枝操作的上界。提高CP 类算法效率的关键工作是分支顺序和定界函数的设计。文献［9］提出了寻找给定子图大小的带有回溯的树搜索算法-。文献［10］提出了带有回溯的树搜索和顶点覆盖相结合的技术。文献［11］提出了一种基于标签类的快速划分算法McSplit（Maximum common induced subgraph Split），利用标签类的划分，快速实现了全局边约束条件。相较传统的存储模式图中每个顶点的值域以及值域过滤的方法，McSplit 算法大幅度降低了内存消耗，将MCS 算法的求解速度提高了若干数量级。

启发式策略是提高基于CP 模型的MCS 算法效率的关键步骤。本文研究围绕顶点冲突关系，解决了确定冲突顶点范围、量化顶点冲突关系等关键问题，设计了基于顶点冲突的顶点匹配顺序。实验结果表明，基于顶点冲突的新匹配顺序可以更有效地解决大规模稀疏图的MCS问题。

1 最大公共子图问题

本章介绍最大公共子图问题相关的术语和基于分支定界的约束模型算法框架［12］。

1.1 相关术语

定义1图G是由顶点的有穷非空集合和边集合组成的，记为G=〈V，E〉。V是图G的顶点集合，E是图G的边集合，（a，b）∈E，（a，b）表示顶点a和b之间存在连接边。|V|表示顶点数，|E|表示边数。

定义2给定模式图Gp=〈Vp，Ep〉和目标图Gt=〈Vt，Et〉，顶点匹配对〈v，w〉是顶点的笛卡儿积，v∈Vp，w∈Vt，且v和w具有相同的标签属性。

定义3给定模式图Gp=〈Vp，Ep〉和目标图Gt=〈Vt，Et〉，最大公共子图问题是找到含有最多顶点匹配对的子图Gs=〈Vs，Es〉，即任意匹配对〈v，w〉和〈k，j〉∈Vs，满足（〈v，w〉，〈k，j〉）∈Es，当且仅当（v，k）∈Ep，（w，j）∈Et。该约束条件也被称之为边约束。

定义4顶点v的邻域是与顶点v有边相连的顶点的集合，记为N（v）。|N（v）|表示顶点v的邻居个数。

定义5顶点域是由模式图和目标图中具有相同标签属性的顶点构成的集合，记为domain。由若干顶点域构成的集合称之为域集，记为Domains。

1.2 基于分支定界的MCS算法

基于分支定界的MCS 算法是带回溯的深度遍历搜索树空间的算法。算法1描述了MCS算法流程［11］。

算法1 MCS（Gp，Gt，Domains）。

输入 模式图Gp、目标图Gt和初始域集Domains。

输出Gp和Gt的最大公共子图。

算法1 的初始域集Domains是根据顶点的标签属性划分的顶点域集合。若输入的Gp和Gt是无向非标定图，那么Domains只有1个顶点域，即包含所有的模式图顶点和目标图顶点。若Gp和Gt是标签图，那么根据不同的标签属性，顶点被划分到不同的顶点域中。curSolution记录搜索过程中的当前解，初始为空；maxSolution是目前为止得到的最优解，初始为空；bound（）返回在搜索树当前分支点，所有顶点域可提供的最大匹配数之和，而每个顶点域的最大匹配数是该域中模式图的顶点数和目标图的顶点数两者之中的较小值。ChooseDomain（）依据启发式策略，从当前域集Domains中选出某个顶点域domain；ChooseV（）则返回依据启发式策略，从domain中选择的模式图顶点v。filterDomains（）将搜索树当前层的域集，依据与分支点的邻接关系，划分产生新的顶点域newDomains。

MCS 的求解过程是:首先根据模式图Gp和目标图Gt的标签信息，建立初始域集Domains，如例1 中的D0。如果当前解大于目前的最优解，那么更新最优解为当前解（第1）～3）行）；否则，计算当前分支层的上界（第4）行）。上界是从树根到当前分支点路径上的匹配对数，与当前域集的最大可匹配对之和。如果上界小于等于目前的最优解，表明该路径不能提供比目前的最优解更好的解，程序进入回溯，搜索树剪枝（第5）～7）行）。

若不满足剪枝条件，算法1 依据分支策略，从当前域集中选择某个顶点域domain，然后再选取模式图中某个顶点v，与目标图中的可匹配顶点w逐一匹配，当前解增加匹配对〈v，w〉，满足边约束条件下，对剩余的顶点域进行划分，并递归调用MCS 函数搜索新分支（第11）～13）行）。遍历完v的所有匹配可能性后，移除v（第16）行）；若当前顶点域不再包含任何模式图顶点，表明该域的所有匹配可能性已被遍历，从域集中移除当前顶点域（第17）～19）行）；然后同样方式遍历其余的顶点域（第20）～22）行）。当算法遍历完搜索空间，全局变量maxSolution记录了最终的最优解。

例1 说明了在搜索过程中，bound（）的计算方法和filterDomains（）产生新域集的过程。输入的模式图和目标图均为无向图。

例1 如图1 所示，模式图Gp的顶点集Vp=｛1，2，3，4，5｝，边集Ep=｛（1，2）（1，3）（1，4）（2，3）（2，5）｝；目标图Gt的顶点集Vt=｛a，b，c，d，e，f｝，边集Et=｛（a，b）（a，c）（a，e）（b，d）（b，e）（c，d）（c，f）｝。

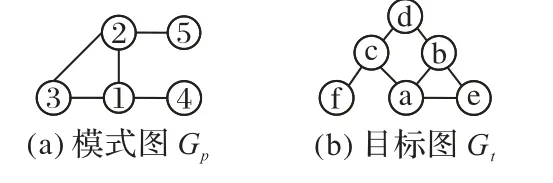
图1 顶点域的图例Fig.1 Instance of vertex domain

因为模式图和目标图是无向图，顶点标签属性相同，所以Gp的每个顶点均可与Gt的顶点匹配，初始域集只包含1 个顶点域D0=｛1，2，3，4，5，a，b，c，d，e，f｝。显然，D0可提供的最多匹配对是5（bound函数的返回值）。依据顶点度的降序策略，首先选择〈1，a〉作为搜索树第一个分支点。根据边约束，产生与分支点〈1，a〉相邻的顶点域D11=｛2，3，4，b，c，e｝，不相邻的顶点域D12=｛5，d，f｝，所以filterDomains返回的新域集是｛D11，D12｝，该域集的bound函数返回值是3+1=4。

2 匹配冲突的学习

绝大多数传统的MCS 算法选择图的静态属性作为分支策略的依据，如顶点邻接性、顶点度、顶点或边的标定值，而基于冲突学习的顶点匹配策略以强化学习的思想为核心，优先选择冲突高的顶点，以加速最优解的计算。

2.1 强化学习

强化学习是智能体与环境交互，从环境中获取学习的反馈信号；通过不断的试错，获得行为的强化信号，最终达到累计奖励最大化的目标［13-15］。强化学习中的要素:智能体、动作、环境、奖励和目标。对于搜索树空间，MCS 算法作为智能体，每次分支动作是在不断地试错，以达到快速找到最优解的目标。如何定义搜索中，分支动作每次获得的奖励？如何获得累计奖励是需要解决的关键问题。

2.2 匹配的冲突

一旦匹配对造成搜索分支提供的最大可匹配对减少，则称之为匹配冲突。匹配冲突代表了匹配动作对搜索环境的影响。例1 中，域集Dold=｛D11，D12｝的最大可匹配对是4。选择〈5，d〉作为第二个分支点，满足边约束条件，D11被划分为D21=｛2，b，c｝和D22=｛3，4，e｝；对D12划分，没有满足边约束条件的新顶点域产生。最终，形成新域集Dnew=｛D21，D22｝，且最大匹配对是1+1=2。Dold-Dnew=4-(2+1)=1，最大可匹配对减少1，其中等式左边的1 代表分支点。同样方法分析，若选择〈2，d〉作为第二个分支点，产生新域集｛｛3，e｝｛4，c｝｛5，d｝｝，4-(3+1)=0，最大可匹配对未减少。

匹配的冲突说明分支顶点的匹配动作对搜索子树的大小具有不同的影响。生成的子树越小，bound函数获得质量更好的上界，算法1 更快达到搜索的叶节点。同时，分析冲突的原因，搜索路径上的每个分支点对当前子图的产生均有作用。从子图的角度分析，搜索树空间相当于是待映射顶点构成的子图。图2 是去除分支点〈1，a〉和〈5，d〉的子图，直观地显示了如果优先选择对环境影响大的顶点进行匹配，那么算法将获得满足边约束条件、更加简单的子空间。

图2 去除分支点的子图Fig.2 Subgraphs excluding branching nodes

3 基于冲突学习的顶点匹配策略

本章基于对匹配冲突的学习，设计奖励函数，使得算法（智能体）获得最大的奖励。

3.1 奖励函数

对于∀v∈Vp(∀w∈Vt)，本文定义顶点的奖励函数来计算顶点每次从环境中获得的奖励，记为Rp(v)(Rt(w))。价值函数用于统计顶点累计获得的奖励，记为Sp(v)(St(w))，且初始化为0。具体地，顶点的累计奖励包括两个部分:

1）顶点v和w的奖励是在完成〈v，w〉匹配后，上界的减少:

其中:Dold表示选择分支之前的域集；Dnew表示顶点v和w匹配后，Dold被划分产生的新域集；bound（）返回分支前、后的最大可匹配数，1 表示匹配对〈v，w〉。获得分支顶点的奖励后，更新顶点的累计奖励。

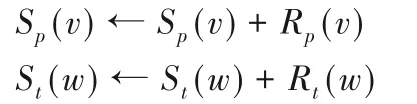
该奖励主要考虑分支动作对搜索环境的影响，上界的差值体现了分支动作造成的影响大小。

2）算法1执行第1）～3）行时，找到了比之前部分搜索获得的解更优的公共子图，而这是由于当前搜索路径上的匹配动作造成的。因此，出现在搜索路径上的顶点获得奖励。对匹配对∈curSolution，v∈Vp，w∈Vt，更新顶点的累计奖励:

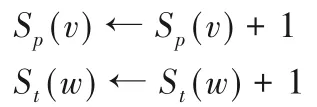
从约束条件进一步分析，依据与分支点〈1，a〉、〈5，d〉的相邻性，图2 中顶点2 与顶点c、b 可以匹配。对于待匹配的顶点，分支点限制了它们是否可以进行匹配，因此，匹配冲突往往是由多个分支点累计造成的。

3.2 新分支策略

引入顶点冲突学习后，采用新分支策略的MCS 算法流程如图3所示。

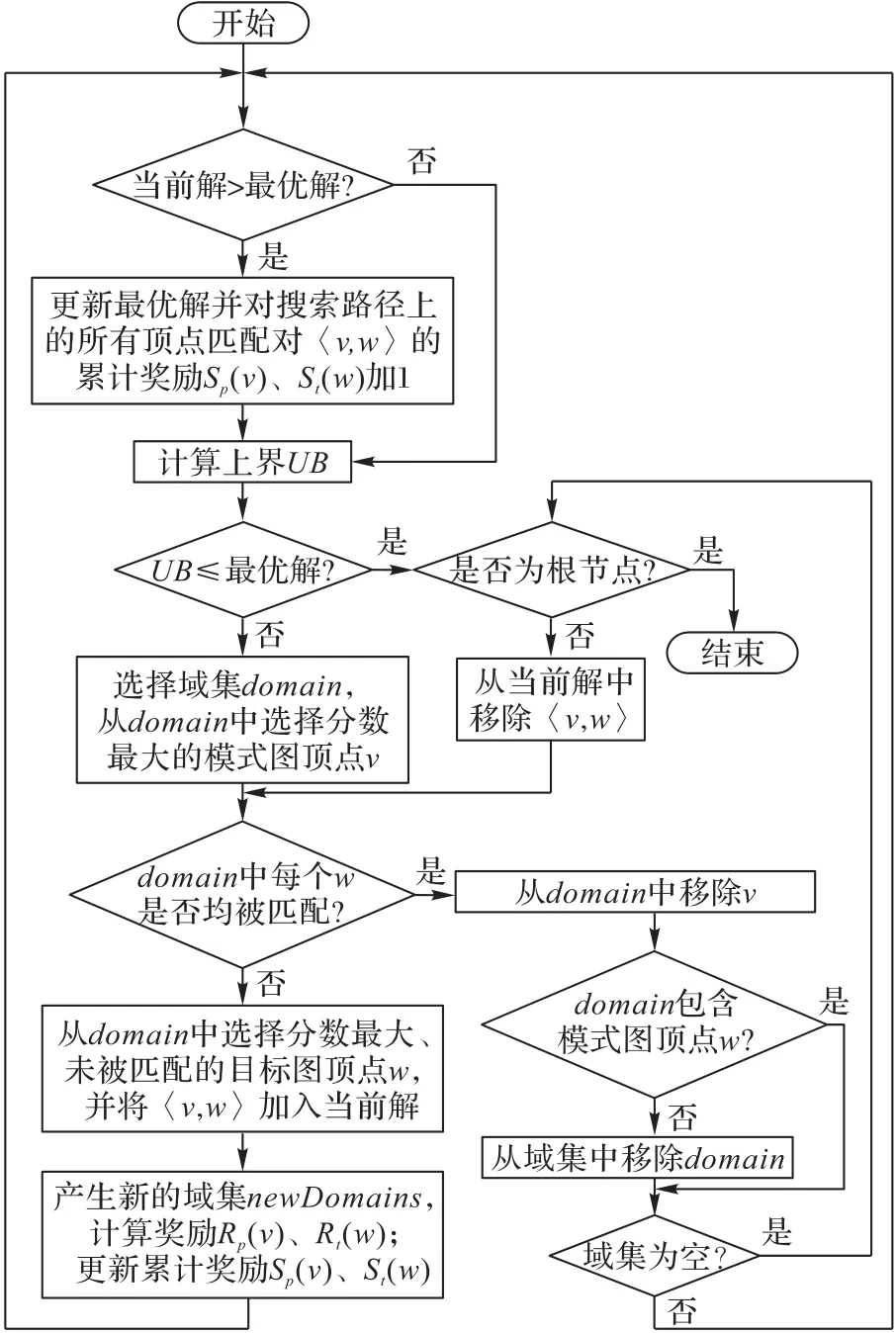
图3 采用新分支策略的MCS算法流程Fig.3 FLow chart of MCS algorithm with new branching strategy

新的分支策略分为两步:首先确定顶点域；其次从该顶点域中分别选择一个模式图顶点和目标图顶点进行匹配。

设域集DS=｛D0，D1，…，Dm｝，分别计算顶点域Di（i=0，1，…，m）中包括的模式图顶点数和目标图顶点数，i=0，1，…，m｝返回匹配操作复杂度较小的顶点域。max 函数返回每个顶点域的模式图顶点数和目标图顶点数两者中较大值，min函数则再取max函数值域中的最小值（算法1中的ChooseDomain函数）。该顶点域的选择策略糅合了最小顶点域策略和邻域策略的优点，既考虑了顶点域中每个顶点需匹配的最大次数，又考虑了最小顶点域。

从被选中的顶点域中，分别选择模式图顶点v和目标图顶点w进行匹配。具体地，优先选择分数最高的顶点v（w），一旦出现平局，则选择顶点度最大的作为分支点。

与传统的分支策略不同，新分支策略不再依赖于图的静态属性顶点度，而是对顶点在历史搜索中产生的影响力进行学习，指导后续的搜索方向。

4 新分支策略的评估

实验平台是Intel Xeon CPUs E5-2680V4@2.40 GHz，内存4 GB，Linux 系统（Ubuntu 14.04）。每个算例的计算限制时间是1 800 s。

4.1 对比算法

实验对比选择了3种算法:

1）McSplit 算法［11］:McCreesh 等［11］于2017 年提出的求解最大公共子图算法，采用了紧凑邻域方法存储每个模式图顶点v的值域，并提出了基于划分产生新的顶点域方法。该算法是目前处于先进水平的MCS算法。

2）McSplitSBS（McSplit Solution-Biased Search）算法［16］:是McSplit的改进版，采用偏好值顺序和记录非优策略。

3）McSplitRLR（McSplit Reinforcement Learning and Routing）算法:本文在McSplit的基础上，采用了基于顶点冲突学习的新分支策略。

4.2 算例集

算例集包含21 543个算例，来自生物化学、图像、地势、无线网格网络等7 种工业问题（算例集下载地址http://liris.cnrs.fr/csolnon/SIP.html）。依据算例是否为有向图，划分为以下两个子集:

1）生物化学（简记为Bio）:来自biomodels.net，有136个有向、无标签图，是描述生物化学反应的网络图。顶点数的范围是9～386。

2）大规模子图同构和最大公共子图算例:包括由随机模型生成或由实际问题转换而来的稀疏图。模式图的顶点数范围是4～900，目标图的顶点数范围是10～6 671，共计12 227 个算例。依据实际问题的来源不同，含有6 278 个Images 算例，1 225 个LV 算例，3 430 个largerLV 算例，24 个PR15 算例，100个Scalefree算例，1 170个Si算例。

4.3 算法对比

表1 给出了3 个算法求解实际问题或随机图的求解个数和平均求解时间对比。第3、5、7 列的数据分别是在限定时间1 800 s 内对比算法求出最优解的算例数，第4、6、8 列则是平均求解时间（单位为s）。平时求解时间=所有被解决算例的CPU时间之和/被解决的算例数。

如表1所示，相较于McSplit、McSplitSBS算法，McSplitrRLR在相同机器和求解限制时间条件下，多解决了109、33 个算例。对于不同类型的算例，对比算法的平均求解时间差异很小，这表明顶点奖励的计算代价较小。McSplitRLR 和McSplit仅分支策略不同，实验验证了新分支策略的有效性。

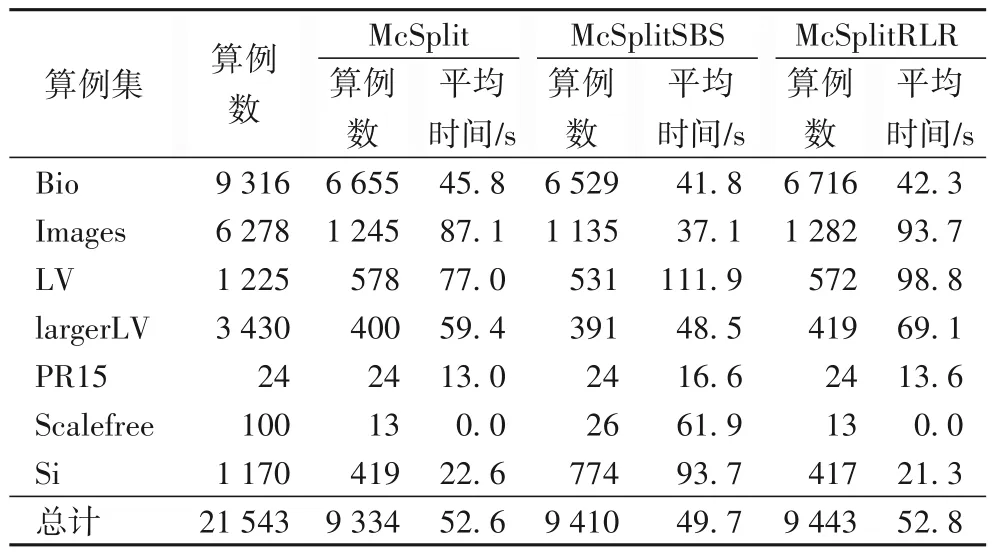
表1 不同算法解决算例数和平均求解时间的对比Tab.1 Comparison of number of instances solved and average solving time of different algorithms

表1 中有7 396 个简单算例均被McSplitrRLR、McSplit 和McSplitSBS 三个算法在10 s 之内解决，平均求解时间依次是0.48 s、0.45 s、0.57 s。这表明三种算法在简单算例上求解效率是同一数量级，冲突学习并未降低求解简单算例的效率。同时，图4 给出了三个对比算法在困难算例求解上的效率，McSplitRLR 比McSplit、McSplitSBS 多解决了5.6%、1.6%的困难算例（算法解决的算例个数-7396），验证了冲突学习策略有效地改进了困难算例的求解。

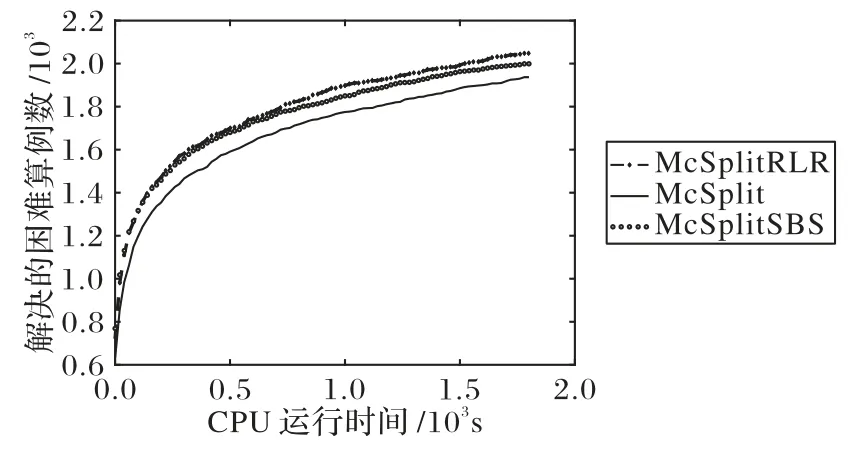
图4 三个算法解决的困难算例数的对比Fig.4 Number comparison of hard instances solved by three algorithms

4.4 结果分析

影响分支定界算法的关键因素是上界和下界的确定。算法1 中第5）行表示当上界小等于下界（maxSolution）时，进行剪枝。如果算法更快地找到最优解则获得高质量的上界UB，在回溯过程中，更有利于满足剪枝条件，提高剪枝率。

图5 显示了对于求解时间大于10 s 的困难算例，在相同的时间内，McSplitRLR 算法相较McSplit 和McSplitSBS 找到了更多算例的最优解。

图5 三种算法第一次找到最优解的算例数对比Fig.5 Number comparison of instances of optimal solution first found by three algorithms

进一步地分析，图6显示顶点的多样性选择有利于算法1更快地找到最优解，并进行有效的剪枝。图6 中每个实心点对应Images 算例集的一个算例，该算例均被McSplit 和McSplitRLR 算法在时间t（10 s≤t≤1 800 s）内解决。实心点的坐标x（y）表示在McSplit（McSplitRLR）算法中顶点被选作分支次数的标准差，即:

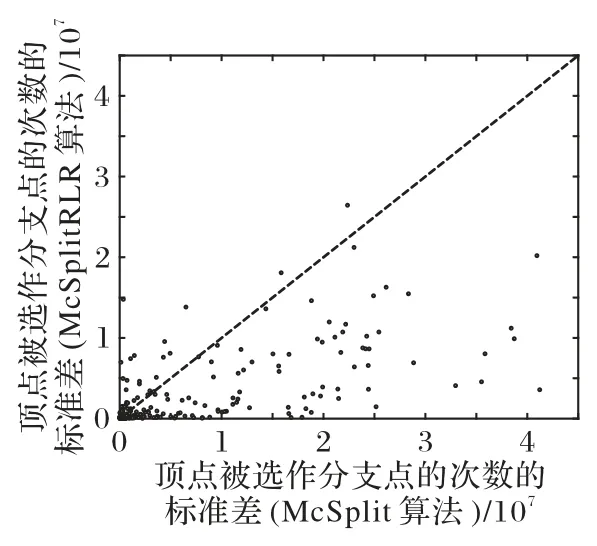
图6 模式图顶点被选作分支点的次数的标准差对比Fig.6 Comparison of standard deviation of number of vertices in pattern graph selected as branch nodes

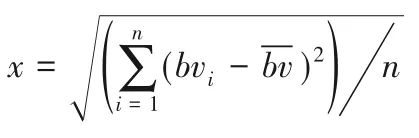
其中:n是在时间t内被McSplit 和McSplitRLR 找到最优解的算例数；bvi表示模式图的顶点vi作为分支点的次数是顶点作为分支点的平均次数

McSplit和McSplitRLR 算法仅分支策略不同，前者每次选择度最大的顶点，而后者每次优先选择累计奖励最大的顶点。在图6中，更多的点出现在副对角线的下方，表明McSplitRLR算法的顶点标准差较小，即在搜索过程中，更多的顶点参与了分支过程，换句话说，基于顶点冲突学习的分支策略给度小的顶点更多的机会。

5 结语

最大公共子图问题是解决众多工业问题的基础子问题，也是经典的NP-难度问题之一。不同顶点匹配动作对于搜索空间有不同的影响程度。本文所提出的基于顶点冲突学习的新分支策略解决了如何衡量匹配动作影响力、计算动作奖励以及使用动作奖励等问题。相较于传统的、基于图的静态属性的分支策略，新分支策略提供了一种新的学习方式和改进基于分支定界MCS 算法效率的途径。学习历史搜索经验和开辟新搜索空间两者之间的关系本质上是探索和利用的平衡。后续将对搜索中出现的局部最优解做进一步的研究。