网络攻击下双层结构多智能体系统一致性

王云燕，胡爱花

（江南大学理学院，江苏无锡 214122）

（*通信作者电子邮箱aihuahu@jiangnan.edu.cn）

0 引言

近年来，层状结构的多智能体系统在万维网、电网、社交网络和基因网络等现实世界的普遍应用成功吸引了众多研究学者的关注。层状网络结构的多智能体系统可通过在层内设计局部控制策略实现系统的全局目标，从而显著降低网络模型设计问题的维数，此外系统模型为符合实际需要还可以设计成分散的形式，故层状网络结构的多智能体系统在各个领域（如控制方面）都得到了广泛研究［1-5］。例如文献［6］中将电力系统建模为由设备层和信息层组成的双层多智能体系统，对电力系统阻尼控制器的性能进行了评估和优化；文献［7］中通过构建节点到节点的通信框架，提出了一种精确协同控制策略来解决工业工厂多个子系统的分布式自适应一致性问题。

本文研究的是由领导层和跟随者层组成的双层结构的多智能体系统，以微电网群优化为例建模：领导层系统为多微电网区域优化自治，跟随者层系统设计主动配电网交互优化策略。以多机械臂电机同步为例建模：领导层系统为多机械臂电机控制，跟随者层设计单机械臂电机控制策略，诸如此类。多智能体系统渗入到现实生活的方方面面，而层状网络的多智能体系统又具有一定优越性，故研究双层网络结构的多智能体系统一致性有很强的理论价值和实际意义。

已有学者进行了双层网络结构多智能体系统相关的理论研究：文献［8］中考虑了领导层和跟随者层包含相同的有向通信拓扑，结合输入时延和李雅普诺夫函数研究了随机抽样下双层多智能体系统的均方点对点一致性问题；文献［9］中针对领导层与跟随者层相同的拓扑结构，采用周期采样和事件触发控制相结合实现了多智能体系统的一致控制；不同于文献［8-9］，文献［10］在领导层和跟随者层系统中给出异构的内部通信拓扑，在通信边受攻击的情形下分析了领导层智能体节点和跟随者层智能体节点间的点对点一致性；文献［11-15］中相应给出了切换、时延和间歇控制下的多智能体系统一致的理论结果。值得指出的是，文献［8-15］中双层网络结构的多智能体系统相邻智能体节点间关系均为友好合作的，然而现实系统中智能体间也会因为矛盾分歧而产生竞争对抗；同样地，双层网络结构的多智能体系统中智能体之间的关系可能同时包含合作和竞争，用符号图刻画既包含友好合作也包含对抗竞争关系的多智能体系统，在一致性协议下，智能体的状态最终趋于模值相同而符号相反的两部分，概括为二分一致性问题。文献［16］中研究了通信边包含合作与竞争关系的多智能体系统的二分一致问题；文献［17］中证明了当有向符号图具有生成树时，系统中智能体能达到区间二分一致；文献［18］中研究了输入饱和情形下多智能体系统的二分一致问题；另外，针对存在干扰、通信拓扑图发生切换等情况，文献［19-22］中给出了多智能体系统二分一致的相关结果；而文献［16-22］中对单层多智能体系统进行研究，考虑到现实系统的多样性和复杂性，本文围绕二分一致问题针对双层网络结构的多智能体系统展开。

在实际应用中，由于通信环境的不稳定，多智能体系统会受到很多干扰，例如网络攻击。网络攻击会破坏智能体与智能体之间的通信链路，从而破坏系统的性能。文献［23］中研究了受攻击的网络化控制系统并应用于电力系统；文献［24］中基于智能体的分布式能量存储系统给出了在网络攻击下的分布式控制方案；文献［25］中研究了传感器损耗和网络攻击下观测器的事件触发一致控制问题。因而研究网络攻击下的双层网络结构的多智能体系统的点对点二分一致问题具有一定的实际意义和理论价值。

基于以上讨论，受已有成果的启发，本文进一步研究双层网络结构的多智能体系统，其中跟随者层系统智能体节点间包含对抗竞争关系。考虑领导层的初始通信拓扑图为非负图，跟随者层的初始通信拓扑图为符号图，基于李雅普诺夫稳定性理论、图论知识和线性矩阵不等式给出了在受网络攻击情形下领导层实现一致、双层网络结构的多智能体系统实现点对点二分一致的充分条件，并对双层结构的多智能体系统进行数值仿真来验证理论的正确性。

本文中所涉及的一些数学符号说明如下：Rn×n表示n×n阶实矩阵集合；In表示n阶单位矩阵；sgn(·)表示符号函数；符号⊗表示矩阵的克罗内克积；λmax(Q)表示矩阵Q的最大特征值，λmin(Q)表示矩阵Q的最小特征值；上标“T”表示矩阵的转置；‖·‖表示向量的欧几里得范数；矩阵P＞0表示矩阵P是正定的。

1 预备知识和主要问题

本文研究一类包含领导层和跟随者层的双层网络结构的多智能体系统，领导层和跟随者层分别包含N个智能体，其中，领导层的智能体只可以接收其他相邻的领导者智能体传递的信息，跟随者层中的智能体既可以接收其他跟随者智能体传递的信息也可以接收领导者智能体传递的信息。两层系统部分对应节点间存在牵制关系。

1.1 图论知识

以下用图论知识［26］符号化双层网络结构的多智能体系统。令G1={V1，E1，A}表示领导层系统的通信拓扑，一个具有N个节点的有向非负图，其中：V1=表示图G1的节点集，节点的下标集合为W={1，2，…，N}；E1={(j，i)：aij＞0}表示G1的边集，aij表示边(j，i)的权值；A=[aij]∈RN×N为G1的邻接矩阵，aij≥0。若图中任意两节点和之间有路径相连，则称G1为连通图。此外，若某个节点与系统中其他任一节点间都存在有向路径，则称图G1包含有向生成树且为根节点。令G2={V2，E2，B}表示跟随者层系统的通信拓扑，一个具有N个节点的符号图，其中：V2=表示图G2的节点集；E2={(j，i)：bij≠0}表示G2的边集，bij表示边(j，i)的权值；B=[bij]∈RN×N为G2的邻接矩阵，bij＞0 时表示智能体节点i和智能体节点j之间是正连接（为友好合作关系），bij＜0 时表示智能体节点i和智能体节点j之间是负连接（为对抗竞争关系），bij=0 时表示智能体节点i和智能体节点j之间无连接。令图G1和图G2的拉普拉斯矩阵分别为RN×N，其中

注1 由于非负图与符号图的定义不同，所对应的拉普拉斯矩阵也不同。考虑到现实生活中事物之间联系的多样性和复杂性，研究包含符号图的多智能体系统更具有实际意义。

定义1［27］若符号图G2的节点集V2存在一组子集k=1，2，…，r，子集满足条件：和=∅(i≠j；i，j∈k)，则称构成了集合V2的一个划分。

定义2［27］若符号图G2中节点集V2存在一个二元划分满足且对于任意节点而对∀vi∈bij≤0，则称符号图G2结构平衡，否则称为结构不平衡。

引 理1［28］若符号图G2结构平衡，则存在S=diag{σ1，σ2，…，σN}(σi=±1，i=1，2，…，N)，使 矩 阵SBS中所有元素非负，其中当时，σi=1；而时σi=-1(q≠r；q，r∈{1，2})。

1.2 模型描述

考虑由2N个智能体组成的双层网络结构的多智能体系统，其中领导层和跟随者层分别有N个智能体，领导层中智能体节点的网络模型描述为：

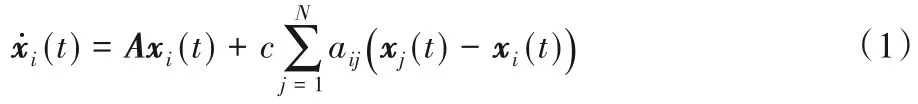
其中：i=1，2，…，N，xi(t) ∈Rn表示t时刻第i个领导者智能体的状态，A∈Rn×n为常数矩阵，aij为智能体与智能体间的连接权重，c为耦合权值。

跟随者层中智能体节点的网络模型描述为：

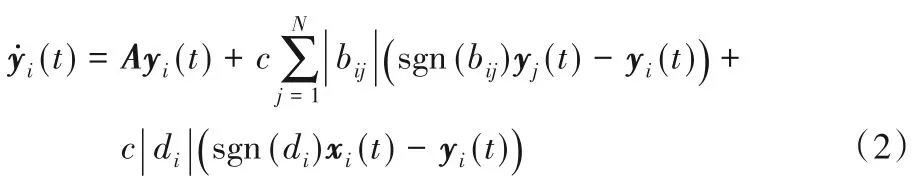
其中：i=1，2，…，N，yi(t) ∈Rn表示t时刻第i个跟随者智能体的状态，bij为智能体与智能体间的连接权重，di表示领导层中第i个智能体与跟随者层中第i个智能体间的牵制权值。

由于通信环境的不稳定，现实系统经常受到各种各样的网络攻击，本文研究受攻击的双层网络结构的多智能体系统的一致性问题。以下举例说明：

图1 可以看出系统在时刻ti(i=1，2，…)受到网络攻击，每次受攻击的时长为τi(i=1，2，…)。受网络攻击时，双层网络结构的多智能体系统的智能体之间的连接边断开，不再进行信息传递，而在攻击结束后多智能体系统重新恢复之前的拓扑结构进行交互。

图1 网络攻击示意图Fig.1 Schematic diagram of cyber-attack

受攻击时领导层中智能体节点的网络模型描述为：

同时，跟随者层中智能体节点的网络模型描述为：

对这个双层网络结构的多智能体系统作出如下假设：

假设1 双层网络结构的多智能体系统不受网络攻击时，领导层通信拓扑图中包含有向生成树。

假设2 双层网络结构的多智能体系统不受网络攻击时，跟随者层中智能体节点存在以领导层中智能体节点为根节点的有向生成树。

注2 考虑到研究的双层网络结构多智能体系统的智能体之间的信息传递方式，领导层的智能体只可以接收其他相邻的领导者智能体传递的信息，跟随者层中的智能体既可以接收其他跟随者智能体传递的信息也可以接收领导者智能体传递的信息，借助图论工具作出假设1 和假设2，具有一定的现实意义。

假设3 双层网络结构的多智能体系统不受网络攻击时，跟随者层通信拓扑图满足结构平衡条件。

注3 对于大规模的拓扑结构，可采用文献［29］中提出的信息分类机制对智能体节点先进行分层简化，再根据定义2中结构平衡的定义来确定符号图是否结构平衡。

假设4 双层网络结构的多智能体系统不受网络攻击时，跟随者层系统连接边的集合包含于领导层系统连接边的集合。

注4 双层多智能体系统相关文献中研究的多为领导层和跟随者层具有相同的拓扑结构，如文献［8-9］，为了拓宽这个限制，同时在文献［10］的启发下，本文假设跟随者层系统连接边的集合包含于领导层系统连接边的集合，具有一定的现实可操作性。

假设5 对任意t0，t≥0，在区间为(t0，t)的时间间隔里多智能体系统受网络攻击的时间|E(t0，t) |满足：|E(t0，t) |≤n0+其中n0＞0，T＞1。

注5 遭受网络攻击的时间过长，会造成多智能体系统瘫痪。考虑实际系统并不会长时间处于受攻击的网络环境中，给出了网络攻击时间的约束条件。

定义3对于任意初始条件，若领导层智能体节点间的状态满足：

其中i=2，3，…，N，则称领导层多智能体系统实现一致。

定义4对于任意初始条件，若跟随者层智能体节点的状态满足：

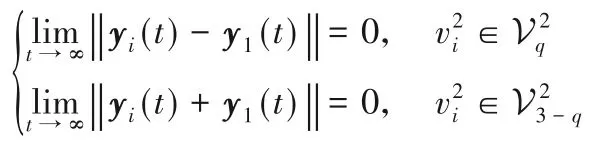
其中i=2，3，…，N，q∈{1，2}，，则称跟随者层多智能体系统实现二分一致。

定义5对于任意初始条件，若领导者智能体和跟随者智能体节点的状态满足：

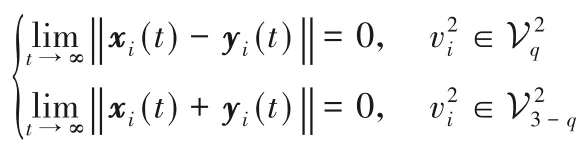
其中i=1，2，…，N，q∈{1，2}，则称双层网络结构的多智能体系统实现点对点二分一致。

2 主要结果

定义领导层多智能体系统节点间的误差：

其中i=2，3，…，N。同样地，定义两层网络结构的多智能体系统间对应智能体节点间的误差：

不失一般性，不受网络攻击时，领导层多智能体系统模型（1）改写成矩阵形式表示为：

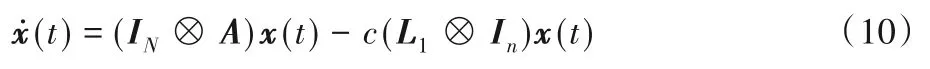
跟随者层多智能体系统模型（2）的矩阵形式表示为：

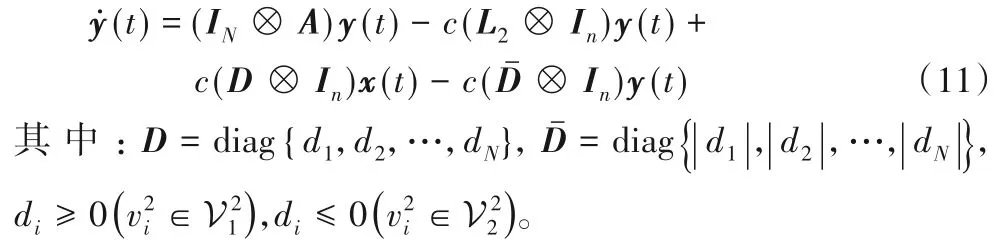
将式（7）求导代入式（10）可得领导层多智能体系统不受网络攻击时智能体节点误差的动力学方程：

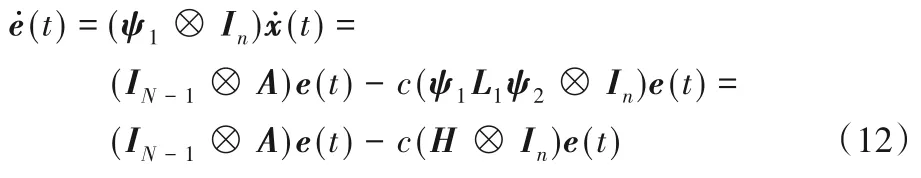
其中H=ψ1L1ψ2。对式（8）求导并代入式（10）、（11）可得双层多智能体系统不受网络攻击时对应节点误差的动力学方程：

根据式（3）、（4）、（7）、（8），可得多智能体系统受网络攻击时：

注6 领导层系统多智能体节点间实现一致，双层网络结构的多智能体系统节点间实现点对点二分一致的问题可转化为证明对应误差e(t)，e～(t)随时间趋于0。

引理2［30］若假设1成立，则存在正定矩阵Π∈R(N-1)×(N-1)，使得ΠH+HTΠ＞0。

引理3［30］若假设2成立，则存在正定矩阵∈RN×N，使得

定理1基于假设1，如果存在正定矩阵Π、P和常数c、T，矩阵P满足线性矩阵不等式PA+ATP≤βP(β＞0)，常数c满足不等式c＞其中λ1=λmin((ΠH+HTΠ)Π-1)，常数T满足不等式T＞，则领导层多智能体系统实现一致。

证明 选取李雅普诺夫函数：

领导层多智能体系统不受网络攻击时，对式（16）求导沿式（12）轨迹可得：

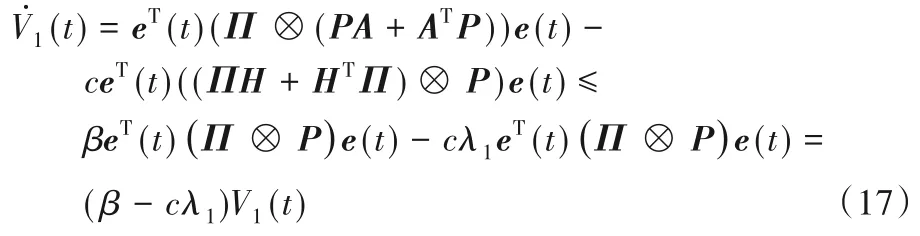
其中λ1＞0。

对式（16）求导沿式（14）轨迹可得领导层多智能体系统受网络攻击时：

而函数V1(t)是连续的，在区间(t0，t)对积分可得其中表示区间(t0，t)不受网络攻击的时长，那么=(t0，t) -|E|，由假设5中的条件可得：

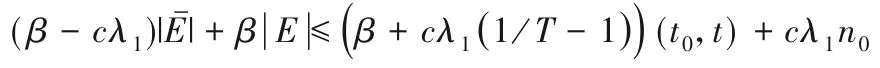
又定理中已知β+cλ1＜0，从而t取足够大时有=0，因此可知0，领导层系统智能体间可实现节点一致。 证毕。

定理2基于假设1～假设5，如果存在正定矩阵、P和常数c、γ、α、T，矩阵P满足线性矩阵不等式PA+ATP≤βP(β＞0)，常 数α＞0，常数c满足不等式条件c＞其中λ2和λ3分别为λ2=常数γ取常数T满足T＞则双层网络结构的多智能体系统实现点对点二分一致。

证明 构造李雅普诺夫函数：

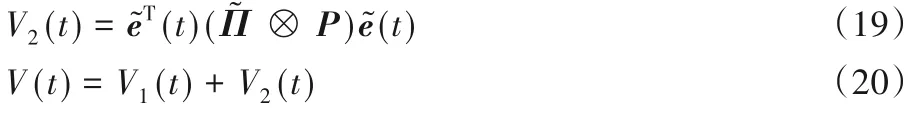
对式（19）求导代入式（13）可得双层结构多智能体系统不受网络攻击时：

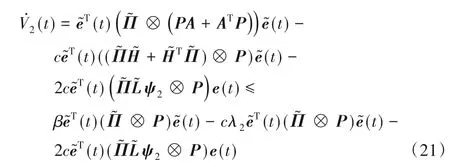
其中λ2＞0。

根据Young’s不等式：

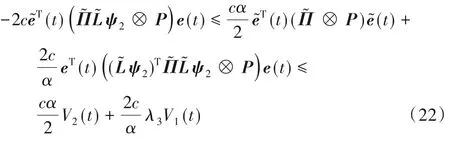
其中λ3＞0。

将式（22）代入式（21）可继续简化V˙2(t)表示为：

对式（19）求导代入式（15）可得双层结构多智能体系统遭受网络攻击时：

对式（20）求导代入式（17）、（23）可得不受网络攻击时：

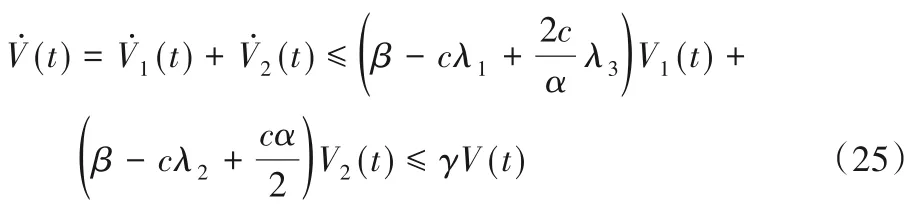
对式（20）求导代入式（18）、（24）可得受网络攻击时：

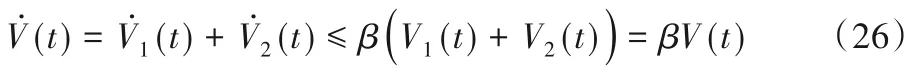
又因为函数V(t)连续，类似地，可得V(t)而，由T＞可 得故t取足够大时有0，从而=0，双层网络结构多智能体系统可实现节点间的点对点二分一致。 证毕。

3 数值仿真

考虑由12 个智能体构成的网络，其中领导层和跟随者层分别有6个智能体，初始拓扑结构如下：

根据图2，领导层智能体节点间的通信拓扑为非负图，跟随者层智能体节点间的通信拓扑为符号图，对应的邻接矩阵分别为：

领导层的智能体1和智能体6与跟随者层的智能体1和6之间有牵制关系，表示为D=diag{0.1，0，0，0，0，-0.1}。从图2 中可以看出，跟随者层智能体可分为两组：={1，2，3}，{4，5，6}，由此取S=diag{1，1，1，-1，-1，-1}。

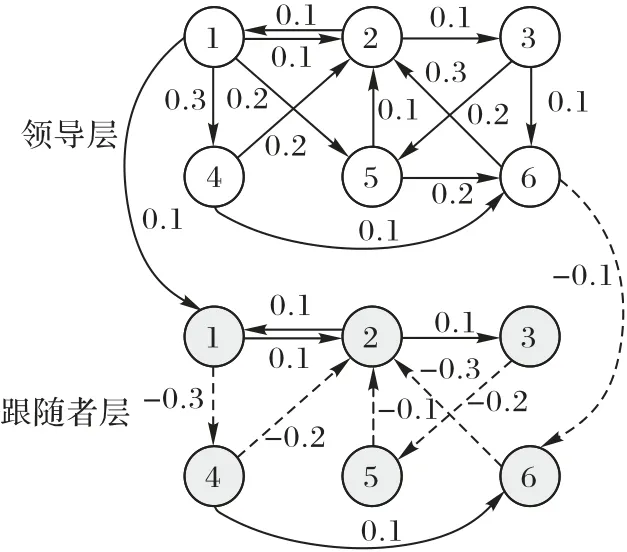
图2 初始通信拓扑Fig.2 Initial communication topology

多智能体系统在二维空间上运动，不受网络攻击时假设领导层系统每个智能体满足：

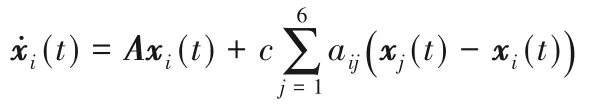
跟随者层系统每个智能体满足：

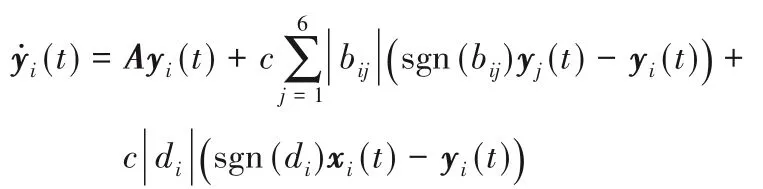
其中：xi(t)=(xi1(t)，xi2(t))T，yi(t)=(yi1(t)，yi2(t))T为二维向量，为简单起见，取A=α=0.06，另外计算可得：

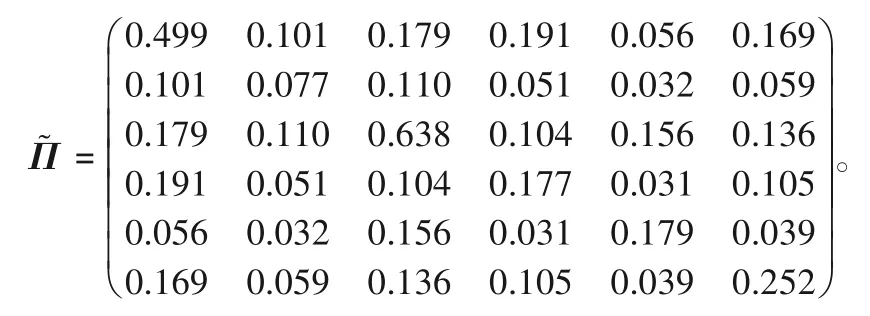
根据以上矩阵求得特征值：

又因为常数c满足定理2中条件：

故取c=80；计算可得：β-cλ1+=-3.292、β-cλ2+=-0.86，由定理2中条件可得γ=max{β-cλ1+=-0.86；另外常数T满足定理2 中条件：=3.4419，故取T=3.5。

以一维分量为例，领导层系统的智能体节点的状态xi1(t)随时间趋于一致，仿真结果如图3 所示。领导层内智能体节点与第一个智能体节点的状态误差ei1(t)随时间趋于0，仿真结果如图4所示。

图3 领导层智能体状态轨迹Fig.3 State trajectories of agents in leaders’layer

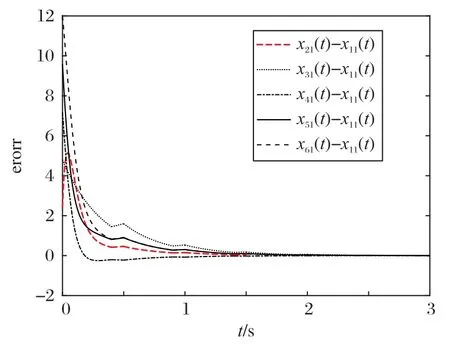
图4 领导层智能体误差轨迹Fig.4 Error trajectories of agents in leaders’layer

从图3和图4可直观地得到结论：领导者层多智能体系统实现了节点一致。

跟随者层系统的智能体节点的状态yi1(t)随时间趋于模值相同符号相反的两部分，仿真结果如图5 所示。跟随者层内其他智能体节点与第1 个节点的状态误差yi1(t) ±y11(t)随时间趋于0，仿真结果如图6所示。

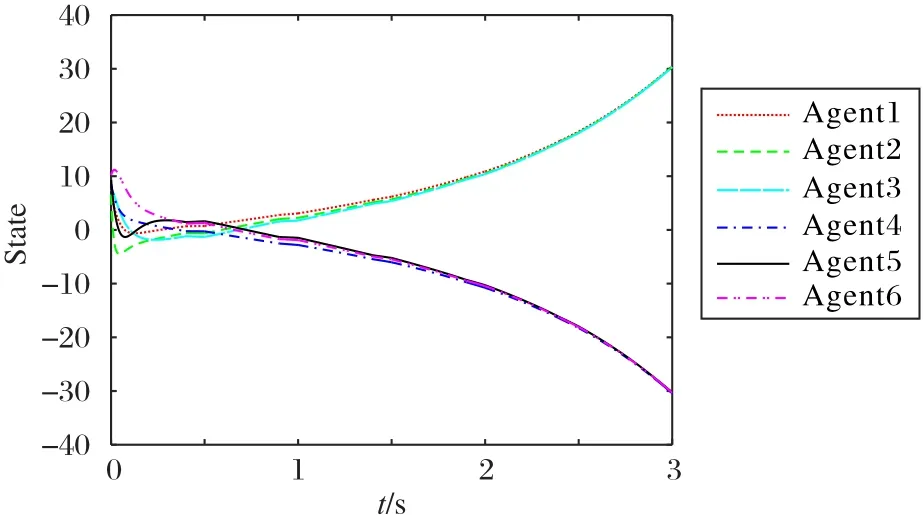
图5 跟随者层智能体状态轨迹Fig.5 State trajectories of agents in the followers’layer

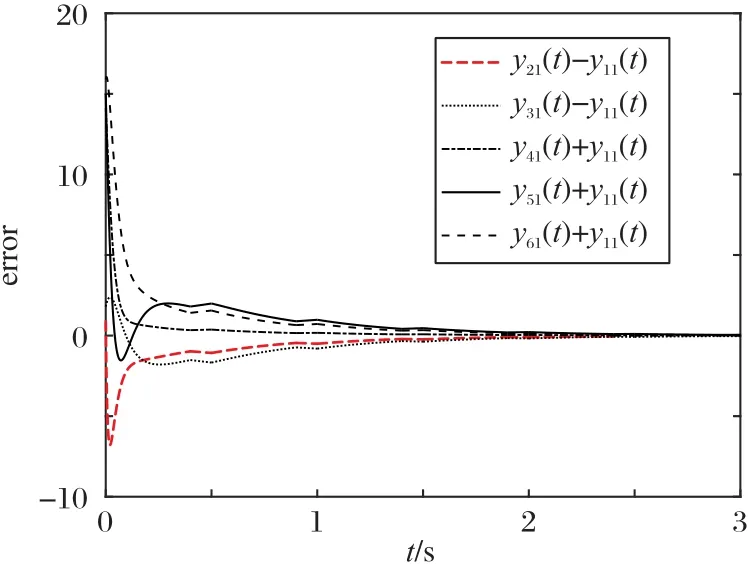
图6 跟随者层智能体误差轨迹Fig.6 Error trajectories of nodes in the followers’layer

从图5和图6可直观地得到结论：跟随者层多智能体系统达到节点二分一致。

另外，领导层智能体节点与对应跟随者层智能体节点的状态误差=xi1(t) -σiyi1(t)随时间趋于0，仿真结果如图7所示。双层网络结构的多智能体系统实现了点对点二分一致。

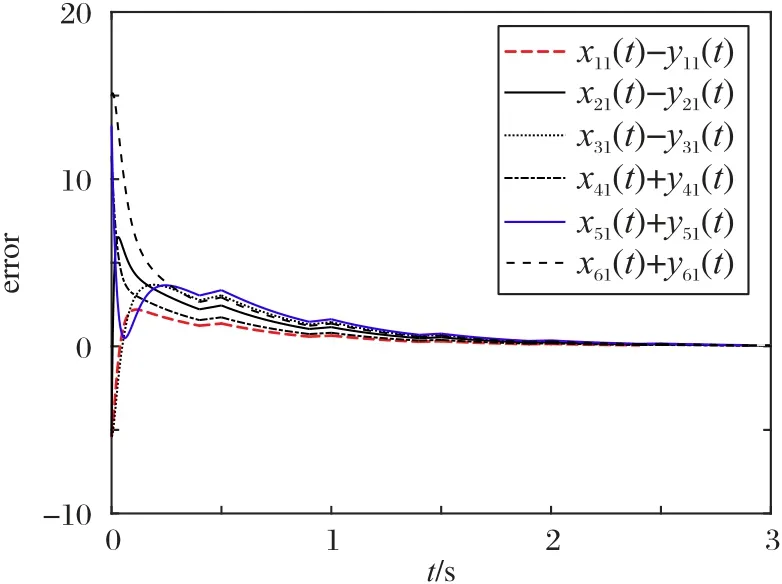
图7 对应智能体节点误差轨迹Fig.7 Error trajectories of the corresponding agents

与文献［8-10］相比，以上系统在跟随者层拓扑结构中智能体节点间关系中增添了负连接，故图5 中跟随者层系统中智能体节点的状态趋于模值相同符号相反的两部分。同样地，不同于文献［10］智能体节点间均为友好合作关系，由定义4、定义5 中对二分一致性、点对点二分一致性的定义，相应地智能体状态误差定义也有所改变，如图6～7所示。

注7 为简单起见，仿真部分选取了包含12 个智能体的双层网络结构的多智能体系统进行分析，领导层和跟随者层分别包含6 个智能体，满足文中所提及的智能体初始状态及一致性协议，在假设1～5 成立的条件下，由图3～7 可以直观地得出结论：双层网络结构的多智能体系统随时间实现了领导层系统智能体节点一致，跟随者层系统智能体节点二分一致，双层系统点对点二分一致，验证了理论结果的有效性。对于包含其他个数智能体的网络拓扑结构，仍可得到类似的结果。

4 结语

本文研究了遭受网络攻击下双层网络结构的多智能体系统的一致性问题，给出了网络攻击下领导层多智能体系统实现一致、双层网络结构的多智能体系统实现点对点二分一致的理论证明；同时给出网络攻击下领导层系统一致、跟随者层系统二分一致和双层结构的多智能体系统点对点二分一致的仿真结果。另外，由于通信网络的复杂性，接下来将进一步研究包含时延、噪声的双层网络结构的多智能体系统的一致性问题。