初中数学几何定理探究案例分析

梁笑韵

摘 要：初中数学有很多定理的教学，有些老师为了提高课堂效率，会把定理直接告知学生，学生运用所学定理去完成练习，这样看上去会比较高效，但是学生对于定理的生成过程比较陌生，容易遗忘，在实际运用中也常有困惑。我认为让学生花时间去参与定理的生成、论证是非常重要的。学生通过归纳总结，可以有效的提高学生学习数学的能力。

关键词：圆周角定理 学生讲题 能力提升

1 学生讲题案例探索（圆周角定理证明）

1、教学内容分析：本节课是在学生学习了圆、弦、弧、圆心角、圆周角等相关概念的基础上出现的，圆周角和圆心角的关系通过弧作为桥梁连接，在圆这一单元有广泛的应用。通过对圆周角定理的探讨，体验知识的形成过程，培养学生严谨的思维品质，为学生提供自主探索与交流展示的空间。

2、教学目标：理解圆周角定理，通过观察比较、发展学生的推理能力，在探索的过程中学会运用分类讨论、转化的数学思想解决问题。

3、教学过程简述

活动一：（1）请学生在纸上画一个圆，在圆上任取两点B和C，用红笔画出弧BC所对的圆心角，然后用蓝笔画出弧BC所对的圆周角，数一数能画几个圆心角、几个圆周角。

设计意图：学生只能画出一个圆心角，但可以画出无数个圆周角。这里给学生提供了一个思考的方向，既然圆心角只有一个，我们在研究圆周角的时候，可不可以把无限个圆周角转化成有限个圆心角呢，这是本定理证明的关键步骤，学生在画图中可以直观感知这一问题。

（2）请同学们把上图所画的圆周角进行分类。

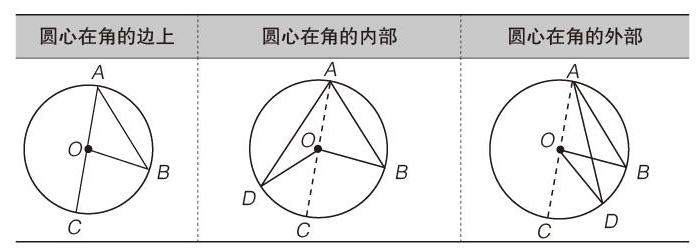
设计意图：让学生通过观察这些角、找出分类的标准。有些同学看到角的分类会联想到把角分成锐角、钝角、直角，但是上图中的所有圆周角都是对着同一段弧BC，所以只有一个角度，学生也会发现按照以前所学的分类方式不合适。教师可以引导学生以圆中固定的点为参照物，观察圆周角与圆心的关系，找出圆心在角的内部，在角的外部，在角的边上这三种情况作为分类的依据。

（3）请同学们到黑板上演示，拖动圆上的点，观察圆心与圆周角的关系，因为我们画图得出的圆周角是有限的，用几何画板演示的情况会更加全面。

设计意图 ：我们在学习几何元素的时候学习了点、线、角，那么用类比的思维我们在圆里面可以找到圆心、弦、圆周角和圆心角。点与直线的位置关系有两种，点在直线上，点在直线外。点与角的位置关系是点在角的内部、在角的外部、在角的边上。在此让学生明白为什么要进行分类研究，而且运用以前所学的点与角的位置关系，从而确定分类的标准，给学生明确了探究的方向。

活动二：请同学们观察图中圆周角和圆心角的关系，大胆猜想，猜想后亲自动手测量验证结论，最后用几何画板演示，根据数据的变化情况能更直观的得出两者间的数量关系。

设计意图：先让学生猜测，培养学生的几何直观能力，然后用量角器测量，培养学生动手操作的能力，最后用几何画板验证，用几何画板演示时，注意改变圆周角的顶点，改变圆心角的大小，改变圆的半径，从多个维度去验证圆周角与圆心角的关系。让学生更加全面的感知信息技术在数学验证中的完整性、准确性、便捷性，提高学生的兴趣。这样的几个步骤可以帮助培养学生探究问题思路，积累数学活动的经验。

活动三：证明一条弧所对的圆周角是它所对圆心角的一半。请同学们分组讨论，然后派代表汇报。

学生上黑版讲解第一种情况的证明思路，并書写过程，以圆为背景的题很多最后都可以转化成三角形的题目，这个证明就用到三角形的外角和定理，我们可以把这个模型归纳为小红旗模型，第二种情况就可以转化为两面小红旗的和的形式，第三种情况可以转化为两面小红旗的差的形式，三种情况的证明思路都是一致的。

设计意图：数学定理的生成只靠测量是不够的，我们也不可能把每一种情况都测量出来。所以我们还需要严谨的证明。学生通过圆周角的定理的生成过程明白了证明几何定理的一般步骤，同时理解了不同的情况需要分类的去证明，这为日后学习其它定理提供了一个范例。通过师生合作 ，让学生学会运用分类讨论的数学方法 、转化的数学思想来研究问题，从而培养学生严谨的思维能力。定理的学习需要学生更多的时间去探索，学生只有掌握了定理的来龙去脉，才能记得牢固，用的灵活，如果教师只重视结果，而轻视了过程，这只是让学生记住了定理，不利于学生思维能力的培养。在教学过程中，学生关于为什么的问题是最有价值的，所以引导学生解决为什么要这样分类是本节课的难点，教师通过类比的思想，让学生原有知识得到迁移，学生理解起来就会更加容易。

2 数学知识与数学思想相结合

数学课堂除了教给学生知识，还要教给学生方法，授之以鱼还要授之以渔，本节课的内容除了圆周角定理外同时还蕴含了多种数学方法。我们如何让学生在课堂上体现这些数学方法呢？

（1）数学中的分类讨论的思想，本节课，圆周角的分类是一个难点，学生是如何想到这个分类呢，课本是通过把圆沿直径折叠的方法，由折痕与圆周角的位置来进行分类。但笔者觉得折痕相对来说清晰度不够，学生不容易发现线与角的位置关系。所以选择让学生观察圆中不变的点（圆心），然后以圆心为参照找出分类的标准，由点与角的位置关系明确了分类的标准。

（2）数学中化归的思想，本节课的三种情况用到了三种证明方法，但三种证明方法可以化归到一种证明方法，所以课堂上要引导学生去观察，建立一个数学几何模型，然后以此来证明后面两种情况。

（3）从特殊到一般的方法，先研究问题的特殊情况，再探索并证明一般性结论。先选择一个特定的圆，找出这个圆上同弧所对的圆周角和圆心角的关系，然后再找出特殊与一般的内在联系，再把特殊情形所获得的结论应用到一般情况，从而获得问题的解决。

灵活运用数学思想是数学素质的重要体现，我们在教学的过程中要以把课本作为研究数学的材料，领悟其中的数学思想，并运用数学思想解决问题。

3 定理的学习方法

数学定理是学习数学的重要基础之一，学生深入理解数学定理、经历数学知识形成过程。数学定理的学习环节：1、了解定理的内容、通过定理能够解决什么问题。2、理解定理的含义、条件和结论。3、定理的证明和推导过程。4、熟悉定理的使用（巩固练习）。5、引申和拓展定理的应用。学生自己发现和证明的定理更容易掌握和记忆，他们才能够去运用数学定理解决问题。

暨南大学附属实验学校 （广东省广州市 510632）