非线性动力方程精细积分法的自适应步长研究
王海波, 纪海潮
(中南大学 土木工程学院,长沙 410075)
1 引 言
钟万勰[1]提出的精细积分方法,为非线性系统的时程分析开辟了崭新的途径;赵秋玲[2]提出了一种非线性系统线性化的精细积分法;张洵安等[3]提出了一种精度较高的线性化迭代精细积分方法;裘春航等[4]将非线性部分用j次多项式来近似;李金桥等[5]先将非线性部分在tk时刻展开成泰勒级数形式,然后将非线性积分项采用泰勒展开法或高斯-勒让德数值积分法与精细积分法结合进行求解;王海波等[6]将精细积分法与Adams-Bashforth-Moulton多步法相结合,提出了一种高精度和高效率的精细积分多步法;李纬华等[7]利用改进的欧拉法对状态变量进行预估及校正,然后结合辛时间子域法对非线性方程进行求解;江小燕[8]根据 Hamilton 变作用定律构造了时空有限元矩阵,提出了求解非线性动力方程的精细时空有限元法;王海波等[9]结合精细积分法和Romberg数值积分,提出了一种避免状态矩阵求逆的高效精细积分单步法;梅树立等[10]利用龙贝格积分法的自适应性解决时间步长的选择问题,提出了结构非线性动力方程的自适应精细积分算法;李健等[11]基于积分区间逐次半分的思想实现了任意时间步长的自适应求积。
本文基于Adams显式和隐式预估公式实现对时间步长的自适应选择,使得时间步长依赖于给定的误差限值。算例证明该思想可以应用于预估型(求解过程需要用到预估公式)精细积分算法,能有效提高计算精度,同时使得算法具有很好的稳定性,能解决刚度软化和刚度硬化问题,具有广泛的适用性。
2 自适应步长的实现原理
2.1 非线性动力方程
非线性动力方程可以表示为

(1)
利用文献[1]的指数矩阵可将其转化为如下同解积分方程,
(2)
式中v(tk + 1)和v(tk)分别为所求解向量在时刻tk + 1和tk的值。
对于式(2),第一项可直接采用精细算法精确得到,计算精度非常高,因此误差的主要来源是对第二项的处理。对于第二项,精细积分算法会用到预估公式,如文献[6,9](先对v(tk + j / 4)(j=1,2,3,4)进行预估,再进行数值积分的一种精细积分算法)。
为数学上叙述方便,对积分方程(3)进行讨论。

(3)
2.2 Adams显式与隐式预估公式
设由r+1个已知的数据点(xn,fn),(xn - 1,fn - 1),…,(xn - r,fn - r)构造插值多项式pr(x),其中fk=f(xk,yk),xk=x0+kh(h为时间步长),运用插值公式有
(4)
(5)
得到r+1阶Adams显式公式,
(6)
(j=0,1…,r)
同理,由r个已知的数据点(xn,fn),(xn - 1,fn - 1),…,(xn - r + 1,fn - r + 1)以及一个未知的数据点(xn + 1,fn + 1),构造插值多项式pr(x),就可以得到r+1阶Adams隐式公式。
2.3 Adams公式的局部误差
y(xn + 1)为真实值,yn + 1为基于预估公式对y(xn + 1)的预估值,误差函数Tn + 1=y(xn + 1)-yn + 1。
构造如下具有p阶精度的预估公式:
yn + 1=α0yn+α1yn - 1+…+αryn - r+
h(β-1fn + 1+β0fn+…+βrfn - r)
(7)
(8)
式(8)右端各项在点xn处作Taylor展开,整理得
y(p + 1)(xn)+O(hp + 2)
(9)
当参数αk和βk满足式(10)时,预估公式达到p阶精度。
(10)
当r=3,p=4,取β-1=0,α1=α2=α3=0,由式(10)可得出其他待定参数的方程组,解之得
(11)
(12)
式(11)是四阶精度的Adams显式公式,式(12)是其截断误差。同理可以得出各阶精度Adams 公式的局部截断误差主项,列入表1。

表1 局部截断误差主项Tab.1 Local truncation error main term
2.4 误差估计及其优点
使用Adams显式公式进行预估,将其结果作为已知的数值点代入Adams隐式公式,再利用Adams显式与隐式公式的局部误差公式,即可得到对一个时间步长的误差估计,下面以四阶精度的Adams显式公式和隐式公式为例。
(13)
fn - 2]
(14)
(15)
(16)
(17)
ξ(xn + 1)=max[abs(ξ′(xn + 1))]
(18)
(19)

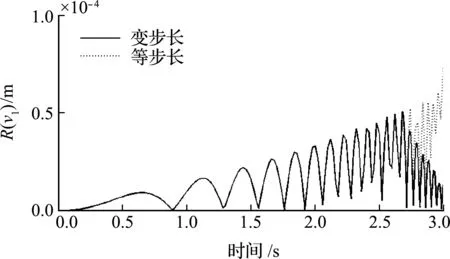
计算时,可调节计算步长,使ξ(xn + 1) (1) 通过选择r+1阶Adams公式及误差限值a,理论上可以实现任意精度的计算结果。 (2)ξ(xn + 1) (3) 式(14~19)的系数均是小于1的数,在进行重复计算时,使得计算误差不会累计扩大,具有良好的稳定性。 在精细积分算法中,预估环节应用本文第2节的内容,即可实现自适应时间步长,本节以四阶精度的Adams公式进行说明。 a的取值决定求解的时间步,进而影响求解精度与效率,在给定a值时,要注意每步局部误差的大小与采用的Adams公式的精度有关,如对于四阶精度的Adams公式,其局部误差的大小是时间步长的5次方。在选定a值时,要根据实际问题允许的误差范围,再结合采用的Adams公式的精度及所希望的时间步长范围综合考虑。 b为根据结构非线性程度控制时间步长缩小的参数,可以在不同的时段内设置不同的b。当函数的阶数越高,就需要越多的控制点才能准确描绘出曲线。求解非线性动力方程得到时程曲线,进而得到位移-时间的函数关系,当某一时间段内的函数阶数较高时,即非线性程度较高时,可以取较小的b值,结果是所取时间步长会较小,该时间步长内的函数阶数就会相应降低,预估的结果更加准确。 图1 算法流程 为便于说明基于Adams显式和隐式预估公式实现对时间步长的自适应选择思想在精细积分算法中的应用,选择以文献[6]为基础,其步骤简单,思路清晰。 采用四阶精度的Adams公式对式(2)的v(tk + 1)进行预估, P(tk+1)=eH Δ tv(tk)+wk (20) 37F(tk - 2)-9F(tk - 3)] (21) (i=0,1,2,3)(22) Ej=eH (tk - j + 1-tk - i) (j=0,1,2,3)(23) 式中Ej(j=0,1,2,3)采用精细算法[1]精确得到。 (24) 令F(tk + 1)=f[m(tk + 1),tk + 1], (25) F(tk - 3)] (26) (27) 给定误差限值a,根据ξ(tk + 1)进行判断, (1) 当ξ(tk + 1)≤a时 (28) 进入下一时间步的计算。 (2) 当ξ(tk + 1)>a时,令 Δt=bΔt,E0=eH Δ t (29,30) 返回式(20)重新进行计算。 式(24)的(Ck-Pk)存在起步问题,对v(t5)进行计算时,令C4=0,P4=0,其做法对结果的影响可以忽略不计。 本方法为多步法,需要用单步法计算表头。 注意,等步长算法是文献[6]提出的一次预估-校正精细积分多步法(Δt=0.1 s);变步长算法是以文献[6]提出的一次预估-校正精细积分多步法为基础的自适应步长精细积分算法(a=0.0001 m,b=0.5,Δt=0.1 s)。 图2中,精确解是指积分步长缩小至能计算出有效位数(一般取小数点后8位)相同的计算结果,下同。 图2 位移时程曲线 从图2和图3可以看出,变步长算法的精度比等步长算法的精度高;由表2可知,在0 s~1 s的时间段内,变步长算法的时间步长小于等步长算法的时间步长;证明了基于显式和隐式预估公式实现对时间步长的自适应选择的思想对预估型精细积分算法的有效性,根据给定的误差限值来决定时间步长的大小,即根据非线性程度的大小决定时间步长的大小,从而提高非线性程度较大时间段内的精度,进一步提高整体的计算精度。 图3 解的绝对误差 表2 各时间段包含时间节点的个数 本节的等步长算法是文献[9]提出的精细积分法(Δt=0.02 s);变步长算法是以文献[9]提出精细积分法为基础的自适应步长精细积分算法(a= 0.0001 m,b= 0.5,Δt=0.02 s)(文献[9]所述精细积分法在每个时间步长中需要对v(tk + j / 4)(j=1,2,3,4)进行预估,可得出ξ(tk + j / 4)(j=1,2,3,4),本文令ξ(tk + 1)=ξ(tk + 1/4)+ξ(tk + 1/2)+ξ(tk + 3/4)+ξ(tk + 1))。 图4 位移时程曲线 图5 解的绝对误差 表3 各时间段包含时间节点的个数 算例1是刚度软化问题,算例2是刚度硬化问题,而且算例1与算例2分别以文献[6,9]提出的预估型精细积分法为基础,两个算例均有很好的效果,故基于Adams显式和隐式预估公式实现对时间步长的自适应选择的思想具有广泛的适用性。 (1) 本文将基于Adams显式和隐式预估公式实现对时间步长的自适应选择思想应用于精细求积算法中,使得算法的计算精度依赖于给定的误差限值,故能根据非线性程度的大小控制时间步长的大小,有效提高非线性程度较大的时间段内的精度,从而提高整体的计算精度。对于初始时间段内非线性程度较大的问题,该思想更加有效。 (2) 应用基于显式和隐式预估公式实现对时间步长的自适应选择的思想能使精细积分算法具有很好的稳定性。 (3) 本文思想应用于精细积分算法中,能解决刚度硬化和刚度软化等问题,具有广泛的适用性。3 自适应时间步长精细积分算法
3.1 流程图及参数分析

3.2 文献[6]+自适应步长
4 数值算例
4.1 算例1




4.2 算例2
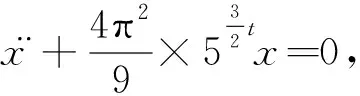


5 结 论

