基于无网格法的非均匀弹性地基上变厚度加筋板弯曲与固有频率分析

杨健生, 曾治平, 韦冬炎, 彭林欣*,2

(1.广西大学 土木建筑工程学院，南宁 530004;2.广西大学 广西防灾减灾与工程安全重点实验室,工程防灾与结构安全教育部重点实验室，南宁 530004)

1 引 言

加筋板具有刚度大和质量小的特点，广泛应用于土木、航天和船舶等工程[1]。这些结构可能发生大变形甚至断裂，采用基于网格(或单元)的数值计算方法求解这类问题存在网格畸变或裂纹与网格线不重合等问题，需要重置网格。

无网格方法不依赖于网格或单元，用于分析上述问题时具有较大的优势。Aghahosseini[2]提出了一种用于分析各种介质类型动态断裂的新型无网格方法，该方法利用了裂纹尖端附近的精细节点配置以及特殊的无网格集成技术。Lin等[3]采用无网格光滑流体动力学粒子(SPH)方法模拟了变厚度功能梯度梁(FGBs)的几何非线性弯曲变形。Peng等[4]采用无网格法对加筋板进行了几何非线性分析。宋彦琦等[5]将基于S-R定理的无网格法从二维发展到三维，并对三维悬臂梁进行了几何非线性分析。王莉华等[6]采用分区径向基函数配点法分析了局部存在高梯度的大变形问题。段庆林等[7]采用基于移动最小二乘近似的一致高阶无网格伽辽金法进行了弹塑性大变形分析。

采用无网格法研究地基板的报道较少，大多集中在地基板自身力学性能的分析，而考虑地基影响的不多。滕兆春等[8]采用微分变化法研究了非均匀Winkler弹性地基上变厚度矩形板的固有频率特性。熊渊博等[9]用无网格局部MLPG(Petrov-Galerkin)方法分析了Winkler弹性地基上正交各向异性板的弯曲问题。夏平等[10]采用无网格局部径向点插值方法(LRPIM)研究了Pasternak弹性地基上中厚板的静力弯曲问题。吴宇等[11]计算了弹性地基上加肋斜板的自由振动频率。

本文采用Winkler弹性地基模型，利用由Belytschko等[12]提出的无网格伽辽金方法，并结合一阶剪切变形理论[13]，对非均匀弹性地基上矩形变厚度加筋板的静力弯曲和自由振动特性进行了研究。

2 变厚度加筋板基本方程

2.1 位移场

根据移动最小二乘法(MLS)[14]近似可得第I个离散节点的形函数在计算点x处的值为

NI(x)=pT(x)A-1(x)BI(x)

(1)

BI(x)=p(xI)WI(x)

式中xI和x分别为离散点与计算点的坐标；pT(x)={p1(x),p2(x),…,pm(x)}为基函数向量，m为基函数个数，本文采用二维二次多项式基函数；WI(x)为权函数，采用三次样条权函数，矩形影响域；N为离散节点个数。

弹性地基变厚度加筋板无网格模型如图1所示。以x方向筋条为例，基于一阶剪切变形理论[13]可得板及x方向筋条的位移场Up和Us x分别为

图1 弹性地基变厚度加筋板无网格模型

(2)

(3)

结合移动最小二乘法[14]近似将板和x向筋条的位移场写成矩阵形式为

(4)

(5)

式中δp I为板上第I个节点的位移参数(不是真实位移)，up I,vp I和ωp I分别为沿x，y和z方向的平动，θp x I和θp y I分别为绕x轴和y轴的转角，δs x i为x向筋条的第i个节点的位移参数，us x i和ωs x i分别为沿x和z方向的平动，φs x i为绕y轴的转角，N和n分别为板和x方向筋条的离散节点个数。

2.2 位移协调条件

离散时板与筋条单独进行互不影响，为了使二者能够成为一个整体协同工作，利用位移协调条件对筋条进行处理。以x向筋条为例，如图2所示，每个筋条节点S在板上都存在一个P点(不一定是板节点)与之对应，二者具有相同的x和y坐标，不考虑板厚度方向的变形，存在式(6，7)两个位移关系，在筋条与板的接触面上存在C点，C,S和P三点具有相同的x和y坐标，存在式(8)的位移关系。

图2 位移协调

[ωx]S=[ω]P,[φx]S=[θy]P,[ux]C=[u]C

(6～8)

利用式(6～8)即可进行筋条与板之间的位移协调，得到协调矩阵Tp和Ts p x，同理可得y向筋条协调矩阵Ts p y，具体协调过程见文献[15]，若改变筋条的位置，只需重新计算矩阵Tp即可，不需要重新计算平板部分。

2.3 非均匀弹性地基模型

采用Winkler弹性地基模型，结合位移场式(4)可得板与非均匀弹性地基之间的接触势能为式(9)，K(x,y)为弹性地基刚度系数，从刚度系数为x和y的函数可知该方法适用于任意形式非均匀弹性地基。

(9)

2.4 弹性地基变厚度加筋板的势能

2.1节通过无网格模型导出了板的位移场式(4)，代入几何方程可得板的平面内应变κp和横向剪切应变λp为

(10)

(11)

式中逗号表示对相应变量求偏导。板的形变势能可以表示为

(12)

h1为图2中板在节点以上部分的厚度，h2为板在节点以下部分的厚度，α=6/5为剪切修正因子，E，G和v分别为弹性模量、剪切模量和泊松比。将板与弹性地基之间的接触势能与板的形变势能叠加得

(13)

筋条用梁模型来模拟，结合2.1节的筋条位移场式(5)与几何方程可以得到x向筋条的形变势能为式(14)，本文认为筋条与板由相同材料制成，即材料常数E，v和G相同。

(14)

式中ws x为x向筋条的宽度，Ss x为x向筋条的横截面积，同理可得y向筋条的势能。将板的形变势能与筋条的形变势能以及板与地基之间的接触势能进行叠加得到弹性地基加筋板的总势能为

(15)

式中Ks x和Ks y分别为x和y向筋条的刚度矩阵。结合2.2节的位移协调矩阵Ts p x和Ts p y，则弹性地基变厚度加筋板的总势能可以表示为

(16)

2.5 控制方程

非均匀弹性地基上变厚度加筋板在横向荷载作用下的总能量为

(17)

由最小势能原理δΠ=0并采用完全转换法[16]对位移边界进行处理后，可得弹性地基变厚度加筋板弯曲的控制方程为

(18)

根据能量法并结合位移协调条件，自由振动时非均匀弹性地基变厚度加筋板的动能为

(19)

根据Hamilton原理并利用完全转换法[16]对本质边界进行处理，得到弹性地基变厚度加筋板的自由振动控制方程为

(20)

3 算例分析

本节通过具体算例进一步分析上述方法的有效性。算例中SSSS，SCSC，SSCC和CCCC分别表示边界条件为四边简支、两对边简支两对边固支、两邻边简支两邻边固支和四边固支，有限元模型均采用S4R单元进行离散。

3.1 收敛性分析

为了验证本文方法的收敛性，采用不同均布节点的离散方案进行计算分析。

一块边长为1 m的正方形平板，板厚h= 0.01 m，弹性模量E=3×106Pa，泊松比ν=0.3，密度ρ=1000 kg/m3。计算该平板在不同节点离散方案情况下的前十五阶固有频率，有限元模型采用30×30个单元离散，结果见表1和图3。

由表1和图3可以看出，随着节点数增多，本文解与有限元结果之间的误差越来越小；所求频率阶数越多则所需的离散节点数也越多，当节点数为17×17时，前十阶频率解与有限元解之间的误差均已小于5%，若只是求解位移，则只需要少量节点即可得到满意的结果，证明了本文方法的收敛性以及收敛速度。

表1 收敛性分析数据(单位：Hz)

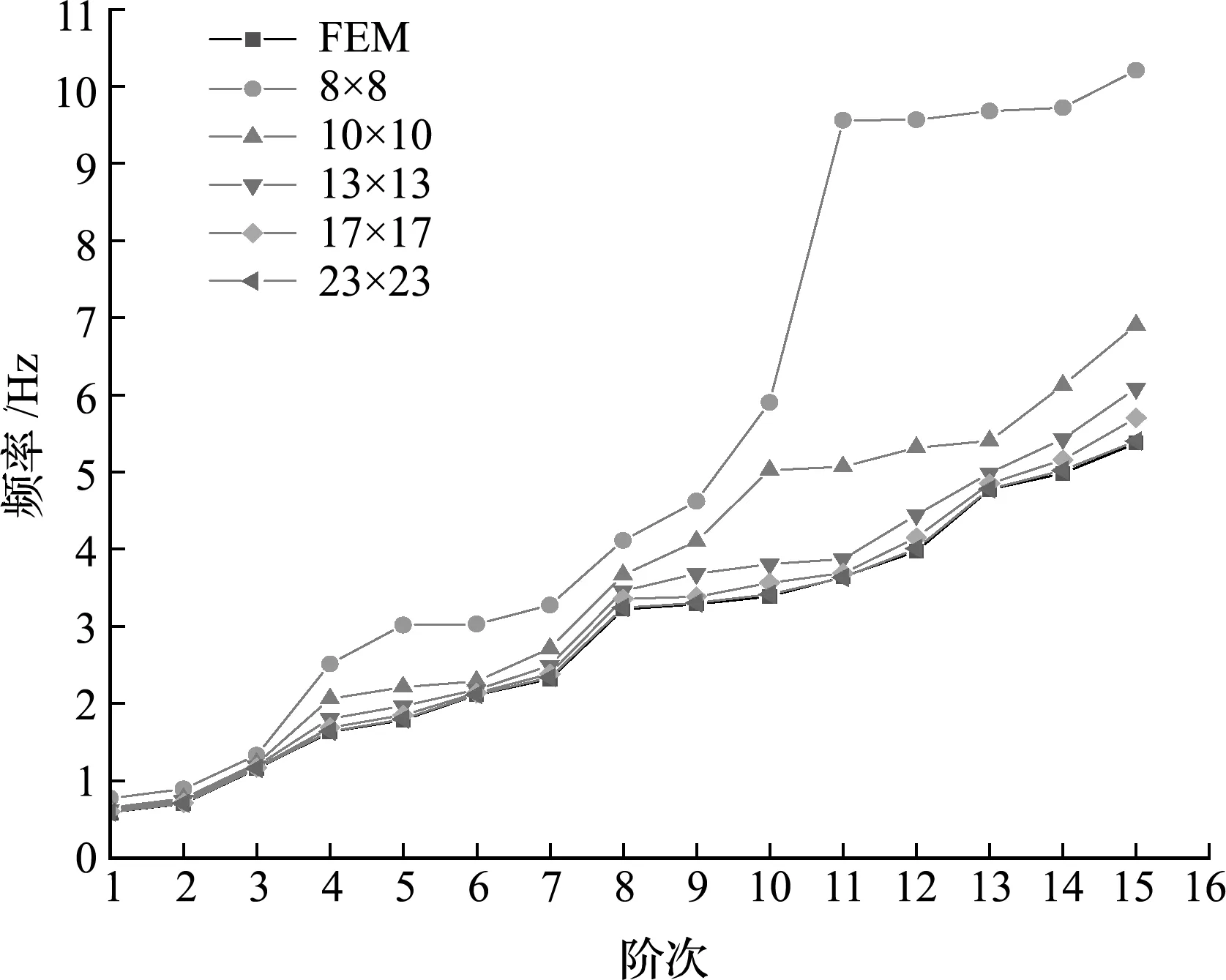
图3 收敛性分析

3.2 有效性验证

3.2.1 变厚度板静力弯曲

尺寸为1200 mm×1800 mm的矩形板，h1=(5+0.005x+0.005y) mm，h2=5 mm，弹性模量E=30 MPa，泊松比ν=0.3，受均布荷载q=0.1 N/m2，采用13×13个均布节点进行离散。计算板在边界分别为SSSS，SCSC和CCCC时的中心点挠度。计算结果与文献[17]的解列入表2。

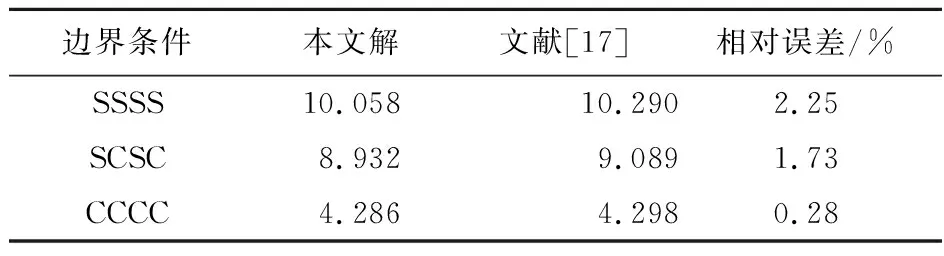
表2 不同边界时的中心点挠度(单位：×10-5mm)

3.2.2 非均匀弹性地基上矩形平板自由振动

非均匀弹性地基板如图4所示，板厚度为h，a/b=1，a/c=0.5，b/h=10，E=2.1 GPa，泊松比ν=0.3，采用17×17个均布节点进行离散。对地基刚度系数K1和K2进行无量纲化处理，分别得R1=K1×b4/(π4D)，R2=0，板的弯曲刚度D=Eh3/[12(1-ν2)]。边界条件为SSSS，计算R1=10，100和1000三种不同情况下的前五阶固有频率。本文解与文献[18]的解列入表3。

图4 非均匀弹性地基矩形板

从以上算例结果可以看出，本文方法在计算变厚度板的弯曲和非均匀弹性地基上平板自由振动问题时都具有较高的精度，验证了本文方法计算此类问题的有效性。

3.3 非均匀弹性地基上变厚度加筋板弯曲分析

有限元网格尺寸取0.05 m×0.05 m。无网格模型板采用13×13个均布节点进行离散，筋条采用13×1个节点进行离散。

尺寸为1500 mm×1000 mm的变厚度矩形板，h1=(15+0.02x) mm，h2=15 mm，弹性模量E=2.1 GPa，泊松比ν=0.3，受q=0.01 N/m2的横向均布荷载作用。在x=250 mm,750 mm,1250 mm处布置筋条，ws=10 mm，hs=50 mm，K1=4×106N/m3,K2=4×105N/m3,K3=4×104N/m3，地基参数如图5所示。分别计算边界条件为SSSS,SSCC和CCCC时变厚度加筋板的控制点弯曲挠度，控制点坐标为1(250,500)，2(750,500)，3(1250,500)，4(750,250)和5(750,750)，如 图5 所示，本文解与有限元解列入表4。

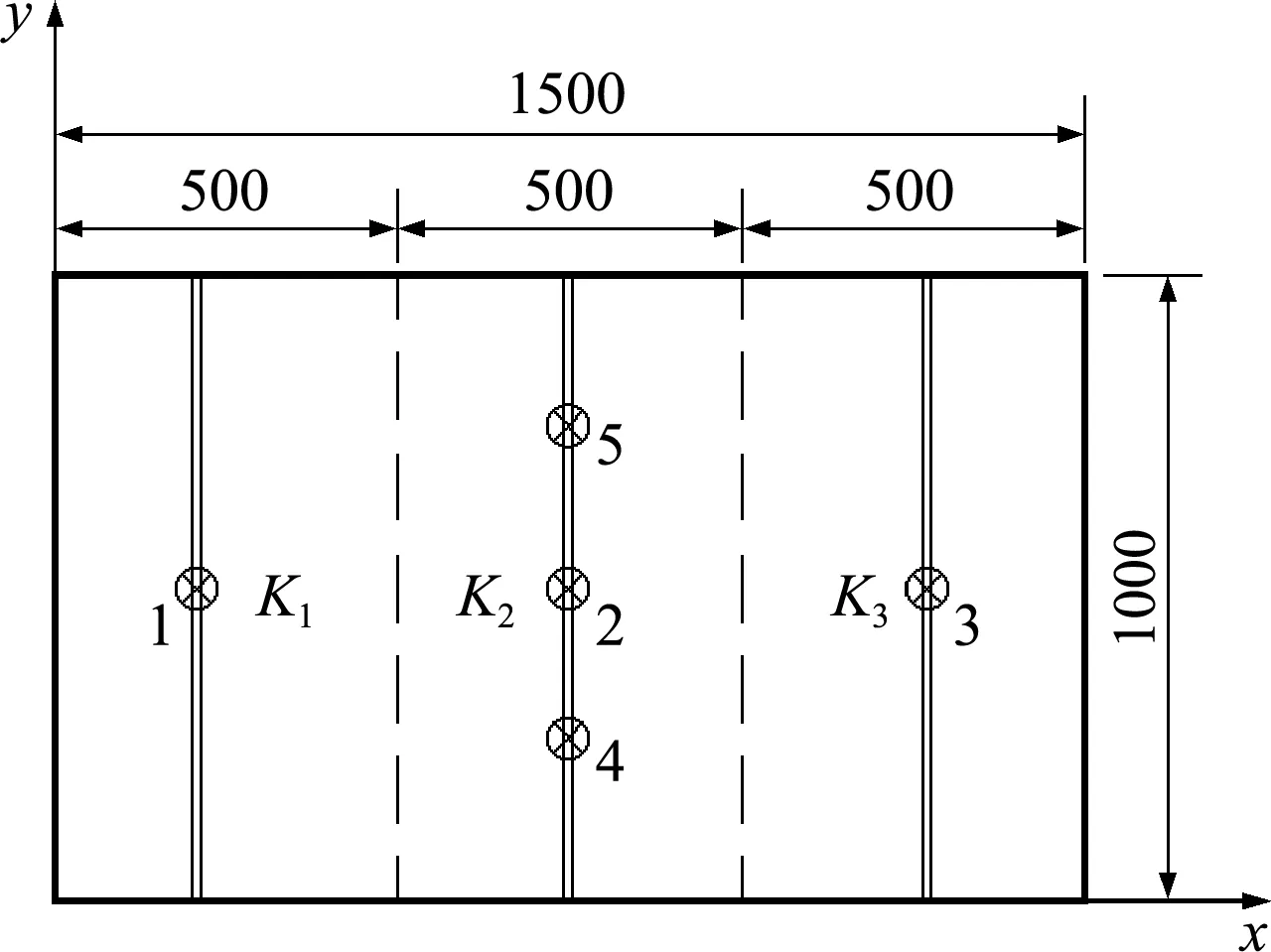
图5 非均匀弹性地基矩形变厚度加筋板

表4 y向三筋条加筋板的控制点挠度(单位：mm)

由表4可知，本文方法分析非均匀弹性地基变厚度加筋板在不同边界条件情况下的弯曲问题时都具有较高的精度。

3.4 非均匀弹性地基上变厚度加筋板固有频率

边长为1000 mm的方形板，h1=(20-0.04|x-500|)mm，h2=20 mm，密度ρ=7800 kg/m3，弹性模量E=2.1 GPa，泊松比ν=0.3，在x=500，y=500处布置筋条，ws=10 mm，hs=50 mm。K1=4×106N/m3，K2=4×103N/m3，地基参数如图6所示。计算在边界条件为SSSS，SSCC和CCCC时自由振动的前五阶固有频率，本文解与有限元解列入表5。

图6 非均匀地基方形变厚度加筋板

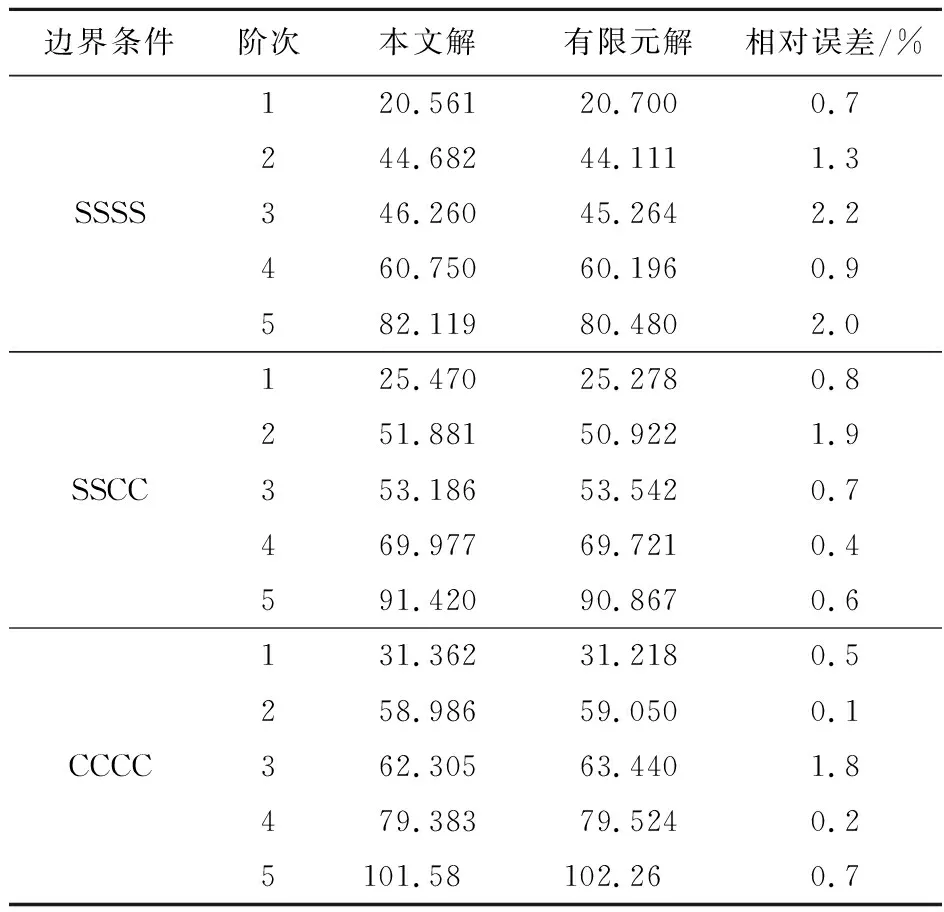
表5 方形非均匀弹性地基上变厚度加筋板的 固有频率(单位：Hz)

由表5可知，本文方法分析非均匀弹性地基变厚度加筋板在不同边界条件情况下的自由振动问题时都具有较高的精度。

4 结 论

本文采用基于移动最小二乘近似的无网格法，同时结合一阶剪切变形理论，计算了非均匀弹性地基上变厚度加筋板的弯曲和固有频率问题，并与有限元及现有文献对比，得出了以下结论。

(1) 所求频率阶数越高则需要的离散节点数越多，使用本文方法，当离散节点为17×17时，前十阶频率解与有限元解之间的误差均小于5%。

(2) 本文解与文献解及有限元解之间的相对误差均小于5%，验证了本文方法分析非均匀弹性地基上变厚度加筋板弯曲及固有频率问题的有效性。

(3) 采用本文方法分析非均匀弹性地基变厚度加筋板弯曲及振动问题，当筋条的位置改变时，不需要重新布置板的离散节点，只需根据筋条的几何位置重新计算转换矩阵Tp，避免有限元法网格重构的问题。可见本文方法在肋条位置重分布的结构优化计算方面具有很大的优势。