不规则波下船舶运动响应特征数值分析

杜一豪，纪 翀，姜胜超，2，顾丹丹，米晓林

(1. 大连理工大学 船舶工程学院，辽宁 大连 116024；2. 大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024；3. 电磁散射重点实验室，上海 200438)

波浪是船舶在海上航行时经受的主要外部载荷，直接影响船舶与海洋结构物在海上的航行状态和工作性能。船舶在波浪中的运动响应一直是船舶水动力学和试验研究的热点问题。长时间以来，人们采用规则波对船舶耐波性问题进行研究，包括船舶水动力性能、波浪载荷和船舶运动响应等问题，并取得了比较完备的研究方法与大量的成果[1-4]。但是，船舶耐波性问题是动力学问题，将真实海况随机波浪简化为规则波的方法实际上是将具有一定频率分布的波浪谱简化为狄拉克函数谱，忽略了大量动力学影响。因此，使用不规则波理论来模拟，才能更为准确地描述出船舶在真实海况的运动响应情况。

目前，大多数研究采用长峰不规则波或短峰不规则波来模拟真实海况。Hua等[5]基于线性理论，采用长峰不规则波研究了船舶在不规则波中的强非线性横摇性能。Carrica等[6-7]使用CFD方法研究了黏性流中船舶在长峰不规则波作用下的运动响应。Luqueth等[8]将黏性流理论中SWENSE方法推广到不规则波6自由度舰船的仿真中。马洁等[9]采用ITTC单参数标准海浪谱模拟了不规则海浪作用下船舶线性横摇、纵摇运动， 讨论了不同船型和不同航态下船舶运动规律。吴乘胜等[10-11]基于黏性数值波浪水池技术对不规则波进行了模拟并研究了船舶顶浪航行的运动响应问题。郑文涛等[12]开展了船舶在随机波浪作用下运动的模型试验，着重探讨了短峰波的方向扩散性对船舶运动的影响。陈京普等[13-14]建立了船舶在长峰和短峰不规则波中时域数值模拟方法，并研究了10万t油轮在长峰和短峰不规则波中的运动响应问题。SHEN等[15]利用URANS-VOF方法对长峰波中船舶运动响应进行数值预测，通过白噪声谱生成入射波进而对船舶运动进行预报。石博文等[16]在利用CFD方法生成具有较高精度的不规则波的基础上，对DTMB5512 船模的顶浪纵摇和垂荡运动进行了数值模拟。相比于规则波，不规则波由于所含的频率范围较大，一旦不规则波列中包含有较多船舶响应敏感的频率成分，则可导致船舶激烈的运动，船舶运动响应规律会更加复杂。

但是目前对不规则波数值模拟的研究，多数只给出船舶运动历时曲线，而对不规则波作用下船舶运动统计规律缺乏深入的研究。实际上，海上波浪变化多样，不仅需要模拟高精度的波浪环境，船舶运动响应的统计学规律对预测实际船舶的耐波性也至关重要。基于线性势流理论，以Wigley型船为研究对象，采用Jonswap谱的长峰不规则波，借助水动力软件HydroStar对随机波浪中船舶升沉、横摇和纵摇运动进行数值模拟，对运动响应的统计学规律进行了深入研究。以5级海况条件为典型计算工况，深入剖析不规则波条件下船舶运动振幅和响应周期等响应规律，并比较了不同波浪谱峰频率对运动响应的影响。

1 控制方程和数值方法

基于势流理论，在流体无黏且运动无旋假设下，对于不可压缩流体，流场存在速度势Φ(x，t)，且满足拉普拉斯方程:

∇2Φ=0

(1)

对于简谐波与结构物作用问题，结构的运动响应也应是同频率下的简谐运动。从速度势Φ(x，t)中分离出时间因子e-iωt，即：

Φ(x，y，z，t)=Re[φ(x，y，z)e-iωt]

(2)

式中：φ为空间复速度势，φ仍满足拉普拉斯方程。对于运动的物体，可以将φ分解为入射势φi、绕射势φd和辐射势φr，即：

φ=φi+φd+φr

(3)

辐射势φr按物体运动的6个分量分解为：

(4)

采用边界元方法进行求解，记φ7=φd，对绕射势和辐射势可建立如下边界积分方程：

(5)

根据式(5)可求得绕射势和辐射势，进而由伯努利方程获得流体压强。通过对瞬时湿物面S进行流体压强积分得到波浪作用力，进一步将其展开到物体表面平均位置Sm，使用线性化伯努利方程得到物体在静水中的湿表面SB上的波浪作用力为：

(6)

式中：ξ为平动位移；α为转角。刚性浮体的运动响应通过刚体运动方程确定：

[-ω2(M+a)-iω(B+b)+(K+C)]{ξ}={fex}

(7)

采用脉动响应函数方法，利用频域下激振力、附加质量和辐射阻尼，通过傅里叶变换求得时域下结构物的运动响应。物体在时域内的方程为:

(8)

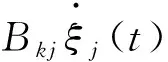
2 数值模拟设置及其验证

采用上述数值模型对细长体Wigley船模型在波浪作用下运动响应展开数值研究，其中，Wigley型船模型定义为：

(9)

式中:Lpp，B，D分别表示静水时的水线长、船宽和吃水。计算所用Wigley船模型尺寸为Lpp=100 m，B=10 m，D=6.25 m，对应其他力学参数及自振频率如表1所示。

表1 船模质量属性Tab. 1 Quality attributes

首先对网格收敛性进行了验证。分别使用3组不同尺寸的网格进行数值模拟，网格数量分别为5 040个(Mesh 1)、9 120个(Mesh 2)和19 040个(Mesh 3)。通过频域求解得到Wigley船的附加质量、辐射阻尼和激振力，如图1、图2、图3所示。从图中可以看出，3组网格所得数据相互吻合较好，证明了方法所采用网格的正确性。综合考虑计算精度和计算成本，数值模拟均采用9 120网格方案(Mesh 2)进行，计算网格如图4所示。

图1 附加质量Fig. 1 Added mass

图2 辐射阻尼Fig. 2 Radiation damping

图3 波浪激振力Fig. 3 Wave excitation force

图4 计算网格Fig. 4 Computational grids

为了验证该数值模拟的可靠性，将数值模拟计算的Wigley船水动力系数与文献[17]中的试验值进行对比，文献中的船模主尺度如表2所示，根据重力相似准则，无因次化后的对比结果如图5、图6所示，可以看到，数值模拟结果与试验值在大部分频率范围内能较好地吻合，说明该数值模拟有较高的可靠性。

表2 文献[17]中船模主尺度Tab. 2 Principal dimensions

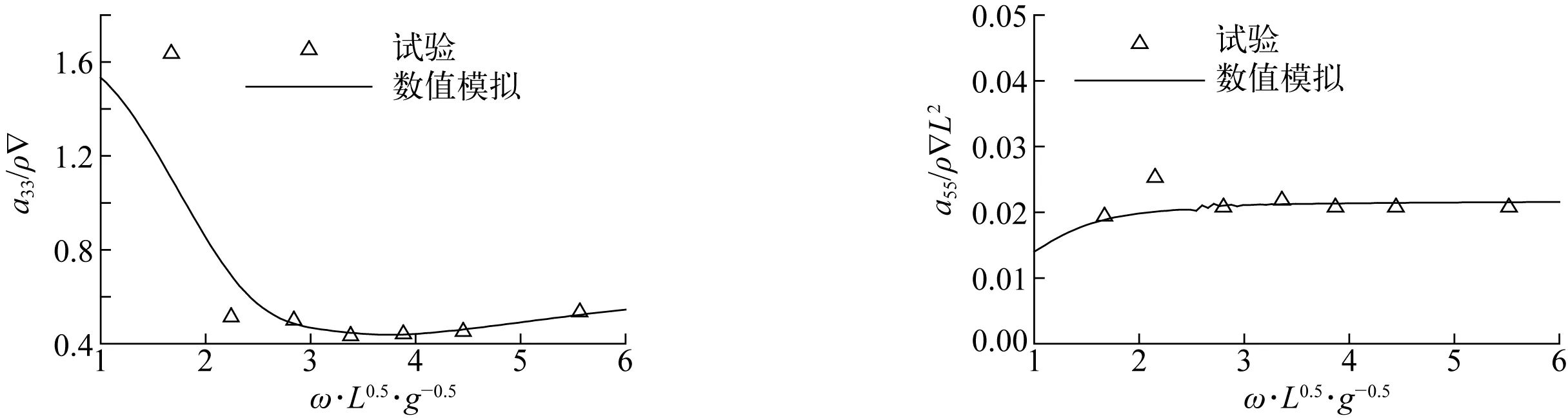
图5 附加质量Fig. 5 Added mass

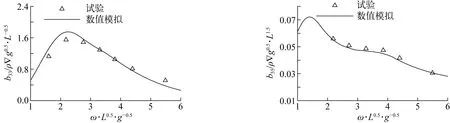
图6 辐射阻尼Fig. 6 Radiation damping

进一步计算求得Wigley船模的升沉、横摇、纵摇RAO曲线，如图7所示，从图中可以看到升沉和横摇曲线峰值频率分别为1.30 rad/s、1.05 rad/s，纵摇曲线第二个峰值频率为1.25 rad/s，与计算所得的自振频率相互符合。

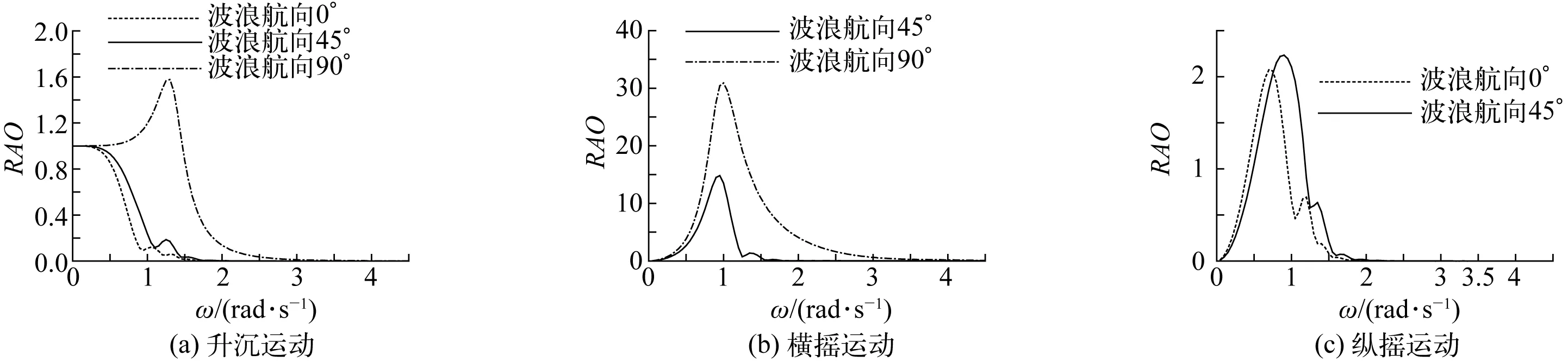
图7 船舶运动RAO曲线Fig. 7 Motion RAOs of ship

3 不规则波条件下船舶运动响应分析

3.1 海况条件与船舶运动响应基本特征

为研究不规则波浪作用下船舶运动响应特征，采用Jonswap谱为入射波浪谱，选取5级海况作为典型海况对船舶运动响应情况进行数值研究，其中，5级海况对应的有效波高和谱峰周期分别为Hs=3.03 m、Tp=6.20 s，实际Jonswap谱如图8所示。在时域模拟中，模拟时长为3 600 s，时间步长取0.1 s。

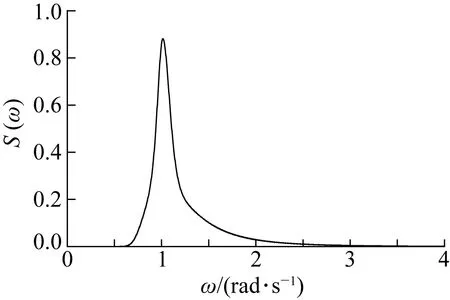
图8 5级海况条件下对应的波浪谱Fig. 8 Wave spectrum of five-level sea state

Wigley船升沉、横摇与纵摇3个方向的典型运动历时曲线如图9所示。从图中可以看出，船模运动振幅呈现出不规则波运动的状态，采用上跨零点法统计三者分别为522、600、534个完整运动响应组成，说明取得的运动响应结果满足不规则波平稳性与各态历经性的统计要求。进一步对1 200～2 400 s、2 400～3 600 s两个时间段的运动响应特征进行统计分析，如表3所示，可以看出，两者统计数据接近，说明1 200～3 600 s时间段内，船体运动已经进入稳定状态，统计结果不随时间的变化改变。上述结果说明文中计算结果可以作为典型运动响应工况进行统计分析。以下分析选1 500～3 000 s时间历程作为样本进行统计。

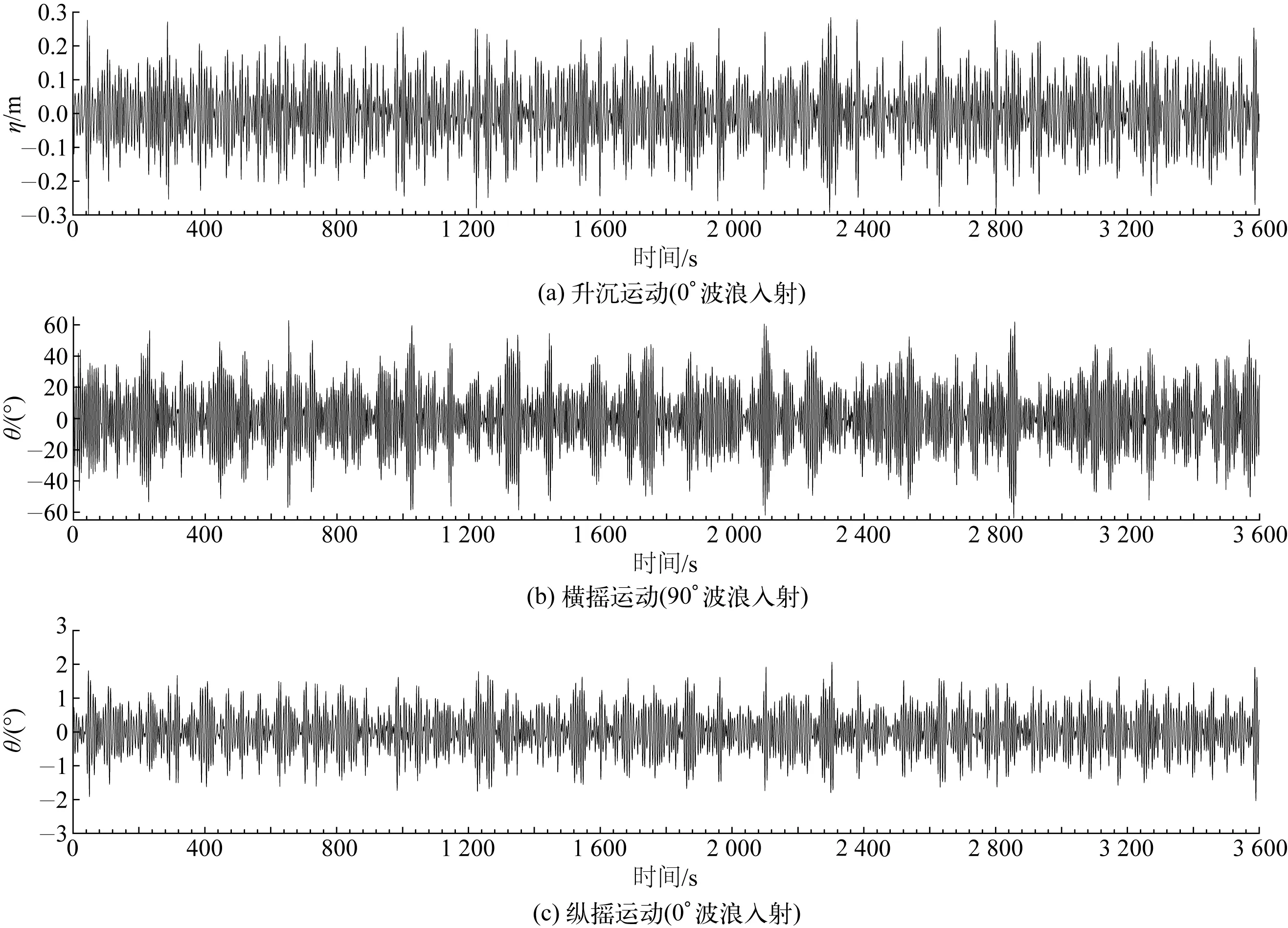
图9 船舶运动响应历程线Fig. 9 Motion responses of ship

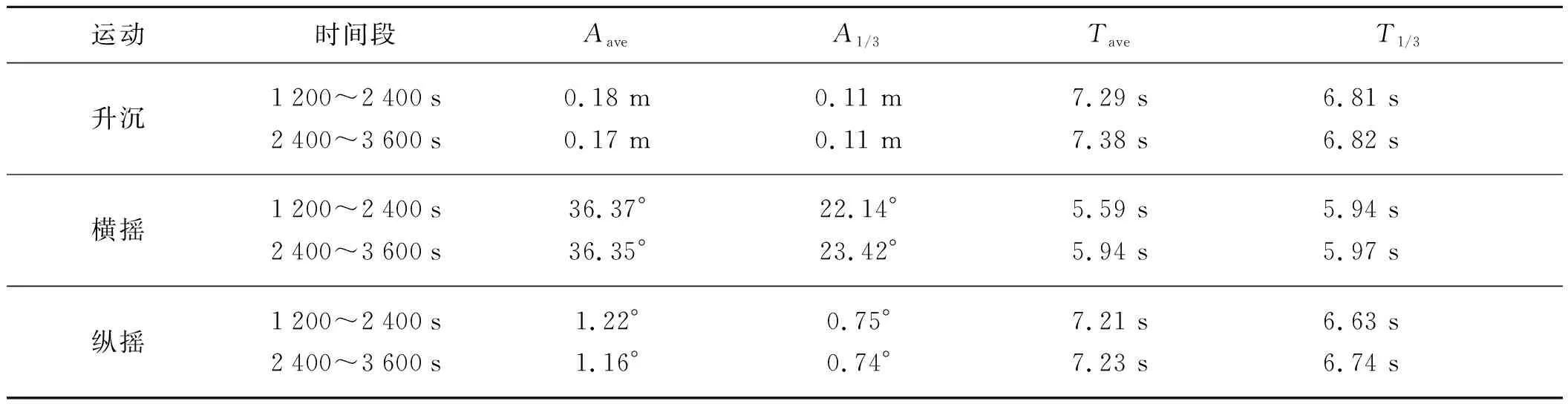
表3 船舶运动响应统计数据Tab. 3 Results of ship motion responses

3.2 船舶运动历时曲线概率密度分析

对样本内船舶运动历时曲线的概率密度进行统计，历时曲线概率密度如图10～12所示，从图中可以看出，船舶升沉、横摇、纵摇3个方向上的运动时间历程概率密度分布基本符合高斯分布，高斯分布位置函数为ζ(t)=0，即船舶平衡位置。

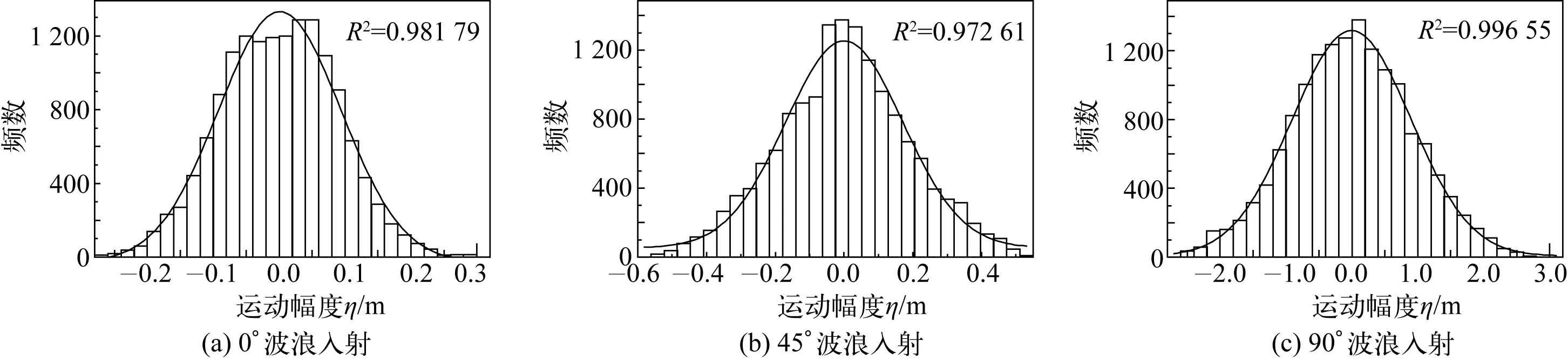
图10 升沉运动历时曲线概率密度Fig. 10 Probability density of heave motion response

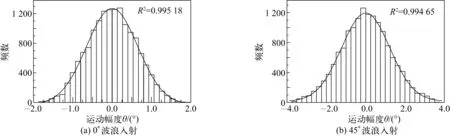
图11 纵摇运动历时曲线概率密度Fig. 11 Probability density of pitch motion response

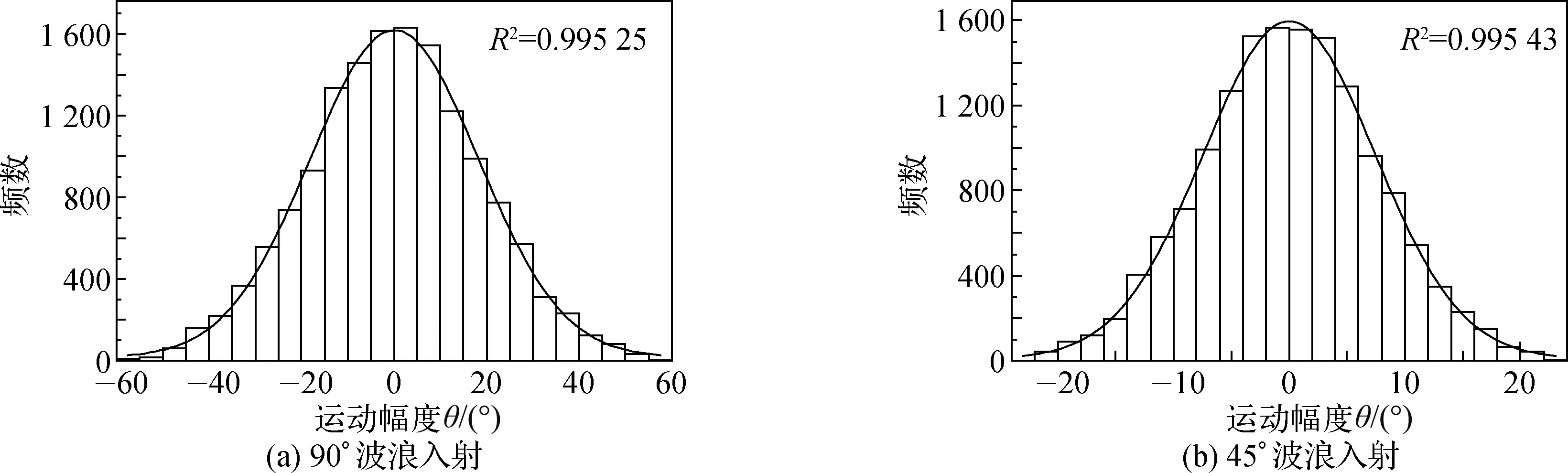
图12 横摇运动历时曲线概率密度Fig. 12 Probability density of roll motion response

进一步对比历时曲线概率密度，可以看出，不同角度波浪作用时，将不同程度的影响历时曲线概率密度的形状。对于升沉运动，对比图10(a)、(b)和(c)可以发现，历时曲线概率密度的形状发生显著变化，图10(a)和(b)中相关系数R2分别为0.981 79和0.972 61，此时R2<0.99，说明此时概率密度分布与高斯分布吻合程度稍差；而图10(c)中R2=0.996 55>0.99，说明此时概率密度分布与高斯分布吻合程度较高。而对于横摇运动和纵摇运动，从图11和12可以看出，历时曲线概率密度的形状变化较小，图11和12中相关系数R2>0.99，说明横摇和纵摇运动时间历程的概率密度分布与高斯分布高斯积分吻合程度较高。此外，不同角度波浪作用会影响不同运动曲线点出现的概率值，并且影响高斯分布的宽度，实际反映了船舶运动最大振幅。以升沉运动为例，从图10可以发现，不同角度波浪作用时船舶运动振幅不同，横浪时升沉运动幅度最大。

3.3 船舶运动响应振幅和周期分布

为了对船舶运动响应振幅进行定量描述，采用上跨零点法对样本内船舶运动振幅与对应周期进行统计，将振幅按照从大到小顺序排列，并给出其对应周期如图13所示。

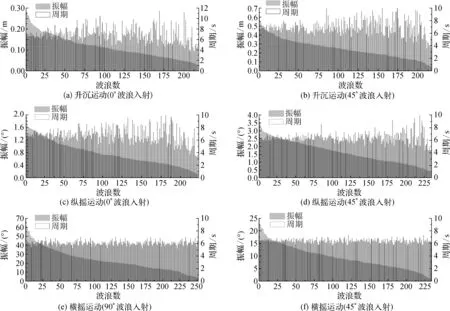
图13 船舶运动幅度分布直方图Fig. 13 Distribution of motion amplitudes and periods

首先从图13(a)和(b)中可以看出，不同振幅所对应的周期不同，具有随机的特征，但结合表5和表6的振幅和周期的统计特征可以看出，对于升沉、横摇和纵摇运动，均有A1/10≈A4%和A1/3(As)≈A13%的统计关系，符合随机过程的统计特征。

从图13(a)～(d)可以看到，船舶升沉和纵摇运动周期离散性较大，但较大的运动振幅对应周期基本相同。表4给出了船舶运动周期标准差的统计数据，记前十分之一大振幅运动对应周期的标准差为σ1，后十分之一小振幅运动对应周期的标准差为σ2。以5级海况波浪0°作用为例，升沉运动和纵摇运动对应的σ1分别为0.37 s和0.33 s，数值较小，说明大振幅响应周期基本相同。结合表5和图13(a)～(d)可以看到，升沉运动前十分之一大振幅响应周期稳定在6.83 s左右，纵摇运动前十分之一大振幅响应周期稳定在6.75 s左右。而σ2分别为1.28 s和2.22 s，数值较大，说明小振幅对应周期差别较大。

而对于横摇运动，从图13(e)和(f)可以看出，横摇运动周期离散性较小。从表4可以看到5级海况波浪90°作用时，σ1=0.29 s，σ2=0.31 s，数值较小，并且σ1≈σ2，说明船舶横摇运动响应周期基本相同，进一步从表5和图13(e)、(f)得知，横摇运动响应周期稳定在6.12 s左右。

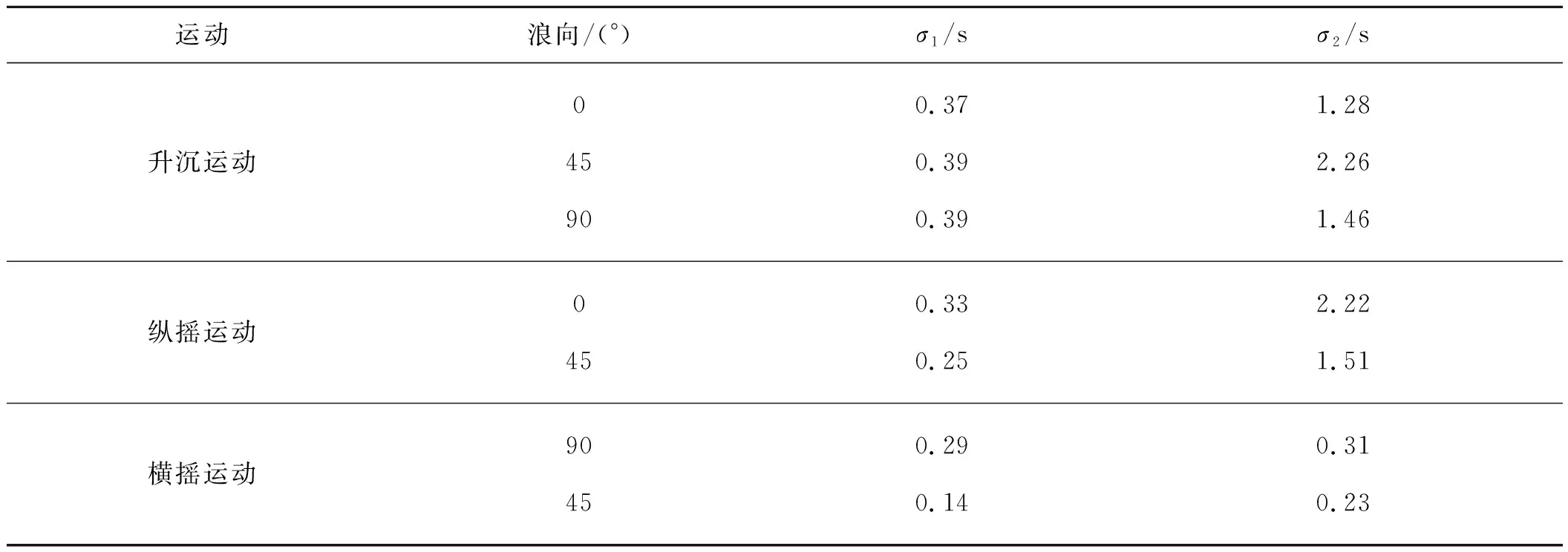
表4 船舶运动周期标准差统计表Tab. 4 Standard deviation of periods

以升沉运动为例，对比不同波浪入射角度下的升沉运动振幅和响应周期，从表5和6可以看到，不同角度波浪入射对应的振幅不同，波浪入射角度从0°到90°，升沉运动振幅A1/10和A1/3显著增大，但对应周期则变化较小，基本稳定在5.7～6.8 s范围内。横摇与纵摇运动振幅和周期变化与升沉运动相似。

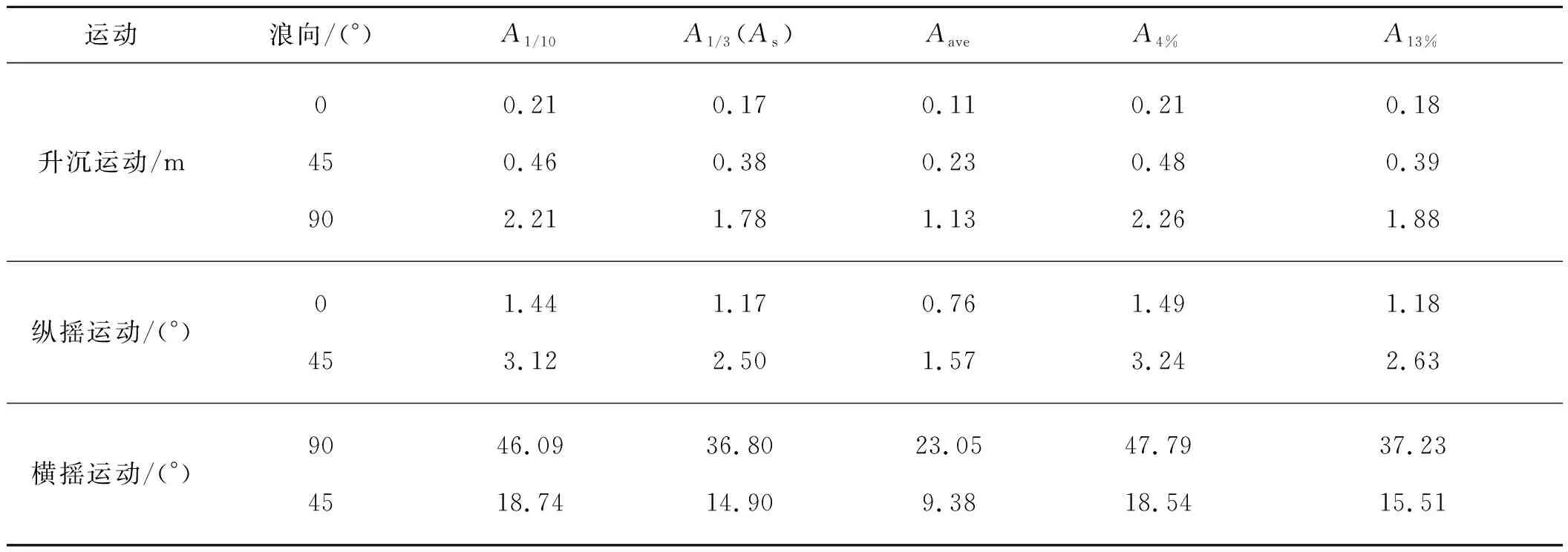
表5 运动振幅统计表Tab. 5 Amplitudes of motion

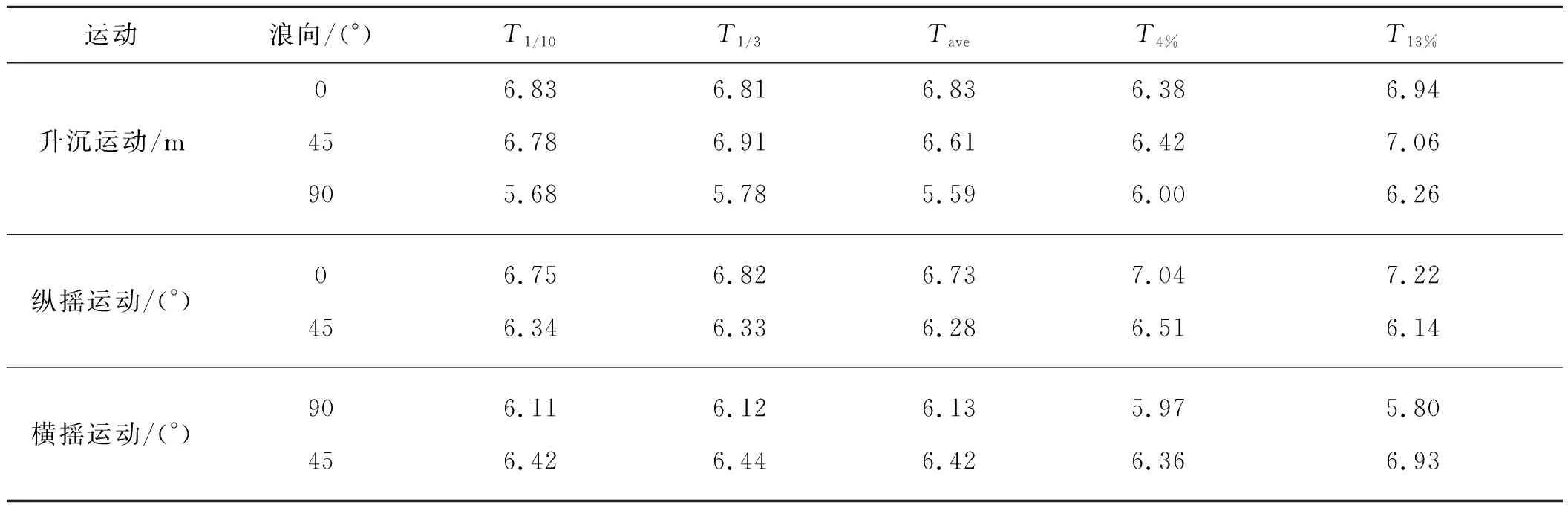
表6 纵摇运动振幅周期统计表Tab. 6 Amplitudes and periods of pitch motion

3.4 不同谱峰频率下的船舶运动响应频谱分析

为考虑不同不规则波浪参数对船舶运动响应特征的影响，基于5级海况，选取有效波高Hs=3.03 m，谱峰频率ωp=0.50 rad/s、1.00 rad/s、1.50 rad/s 条件下船舶运动进行数值模拟，波浪谱如图14所示。采用快速傅里叶变换(FFT)算法分别对3种不同谱峰频率作用下船舶运动历时曲线进行分析，获得运动响应频谱曲线，并与波浪谱曲线进行对比，如图15所示。从图中可以看出，波浪谱峰频率可以对船舶运动响应频率产生显著影响。对于升沉与纵摇运动的情况，ωp=0.50 rad/s条件下波浪谱与船舶运动响应谱几乎重合。当ωp=1.00 rad/s与1.50 rad/s时，船舶运动响应频率均呈现双峰的特征，其中高频峰值出现在船舶自振频率附近，说明升沉和纵摇运动在波浪谱峰频率和自振频率范围内运动。

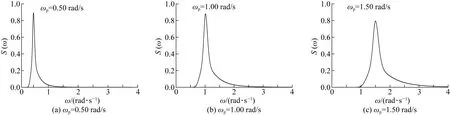
图14 不同谱峰频率对应的波浪谱Fig. 14 Wave spectrums of different peak frequencies

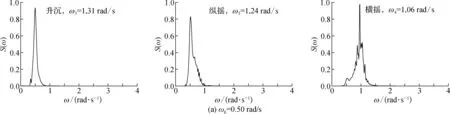
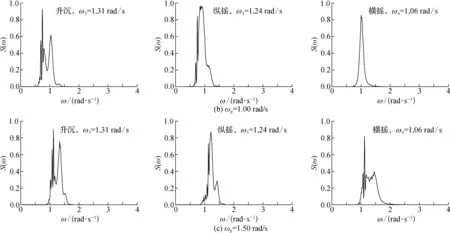
图15 运动响应频域分析结果Fig. 15 Analysis results of motion response in frequency domain

对于横摇运动的情况，在横摇自振频率，即ω4=1.06 rad/s附近，船舶运动频率均出现较大峰值，包括谱峰频率为ωp=0.50 rad/s与1.50 rad/s时的情况。进一步分析可以看出，当ωp=0.50 rad/s时，谱峰频率低于船舶自振频率，船舶运动响应谱在0.50 rad/s附近没有明显的峰值，运动响应谱仍为单峰特征，说明低频波浪能量对横摇运动贡献较小，横摇运动依然主要按照自振频率运动；当ωp=1.50 rad/s时，谱峰频率高于船舶自振频率，船舶运动响应谱在波浪谱峰频率附近存在明显的峰值，运动响应谱呈现双峰的特征。

4 结 语

采用数值方法，对不规则波浪作用下Wigley型船升沉、横摇和纵摇运动响应进行了模拟研究，采用统计学方法对时域运动响应特征进行了统计分析，通过分析比较运动时历的概率密度函数、运动振幅和响应周期的分布变化情况以及频谱变换的结果，得到了船舶运动的统计规律。数值结果表明，在不规则波作用下，船舶升沉、横摇、纵摇3个方向上运动时间历程的概率密度函数均基本符合高斯分布。船舶横摇方向与升沉及纵摇方向随机运动的响应特征有显著差异。在升沉与纵摇方向，波浪谱峰频率远离自振频率，前十分之一大振幅运动对应周期离散性较小，基本稳定在波浪谱峰周期附近，但小振幅运动周期分布离散性较大。而在横摇方向，波浪谱峰频率与自振频率相耦合，不同振幅的横摇运动响应周期均稳定在自振周期附近，且周期离散性较小。傅里叶分析表明，船舶运动频谱与入射波浪谱有显著差异，主要体现在船舶运动自振频率附近出现较大的频谱峰值。通过改变谱峰频率，比较船舶运动响应频谱发现，谱峰频率为0.50 rad/s时，升沉和纵摇运动主要依照谱峰频率运动，响应谱能量集中在0.5 rad/s附近；谱峰频率为1.50 rad/s时，升沉和纵摇运动频率主要分布在1.25～1.50 rad/s范围内。而谱峰频率在0.50 rad/s和1.50 rad/s时，横摇运动频率则均包含自振频率和谱峰频率。总之，不规则波作用下船舶横摇运动响应与升沉和纵摇方向具有不同的统计特征。文中的研究方法可适用于船舶在不规则波中的6自由度运动，为船舶时域运动预报提供了重要参考依据。