不规则波作用下沿岸流流速分布规律分析

王国玉，张 琪，赵银林

(大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024)

人们对于沿岸流的研究有悠久的历史，总结起来有以下三种研究方法：现场观测、物理模型试验和数值模拟。由于波浪具有瞬变性，现场观测资金投入大且开展困难，当前最主要的研究方法为物理模型试验和数值模拟。物理模型试验工作主要包括Visser[1]进行的1/10、1/20两种坡度地形的规则波沿岸流试验；Reniers等[2]进行的高斯型沙坝规则波和不规则波沿岸流试验；Hamilton和Ebersole[3]进行的1/30坡度地形下规则被和不规则波的沿岸流试验；沈良朵等[4]所作的1/40、1/100两种坡度地形的规则波和不规则波的沿岸流试验。数学模型可分为如下两类：一类是基于Boussinesq方程所建立的沿岸流方程，如李绍武等[5]将基于完全非线性Boussinesq方程的波浪破碎模型应用于沿岸流计算中；房克照等[6]基于高阶Boussinesq水波方程，建立了波生沿岸流的时域数值模型，并分析了不同波浪入射条件对沿岸流的影响。此类模型在求解过程中需要设置造波、消波以及反射等边界，且计算相对费时。另一类是基于辐射应力得出的近岸波生流模型，如汪求顺等[7]通过SWAN模型模拟了近岸岛屿附近的波浪场，从而为沿岸流模型提供波浪条件参数；张明亮等[8]在模拟湿地海域波浪和沿岸流的运动特性时，波浪模型为潮流模型提供辐射应力、波高和周期等参数；孙涛等[9]通过求解高阶近似化缓坡方程，获得波浪场信息，通过辐射应力建立沿岸流模型。基于对模型设置和求解速度的考虑，将采用第二类数学模型分析沿岸流。虽然Longuet-Higgins[10]基于辐射应力给出流速公式，但该公式需要将波浪由深水推算至浅水。因此为了便于工程参考与应用，将给出由深水波浪要素及岸坡坡度表达的不规则波浪作用下的沿岸流流速分布规律描述。

1 模型简介与验证

1.1 模型简介

MIKE 21 PMS是对椭圆型缓坡方程的抛物线近似。在求解范围较大的波浪场时，椭圆型缓坡方程的计算工作量较大，而抛物化近似可有效地避免这一问题。一般的，椭圆型缓坡方程可以表示为：

(1)

式中：C和Cg分别为相速度和群速度；φ为平均自由面的速度势；k为波数；W为耗散项，其数值为Ediss/E，Ediss是平均能量耗散率；ω为波浪的圆频率。而抛物化近似的前提是假设一个主要的波浪传播方向，如x方向，并忽略该方向上的散射和衍射以减少计算量。该模型可计算得到整个模拟区域内波高及波浪辐射应力的变化情况，而辐射应力的结果作为波生流的输入条件，从而进行沿岸流的模拟。设置波生流的基本方程在连续性方程和动量守恒方程的基础上进行如下假设：沿岸(y轴)方向流动均匀、稳态条件和辐射应力沿岸分布均匀。

于是x方向上的动量守恒方程可以表示为：

(2)

y方向上的动量守恒方程可以表示为：

(3)

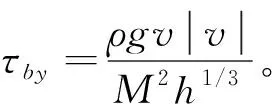
1.2 模型验证

数学模型的验证基于沈良朵[4]开展的沿岸流物理模型试验数据。试验在55.0 m×34.0 m×1.0 m(长×宽×高)的水池中进行，试验参数如表1所示。试验地形坡度1/100时，水深0.18 m；岸坡坡度1/40时，水深0.45 m。岸坡模型与造波机成30°。试验中的不规则波浪采用Jonswap谱进行模拟。

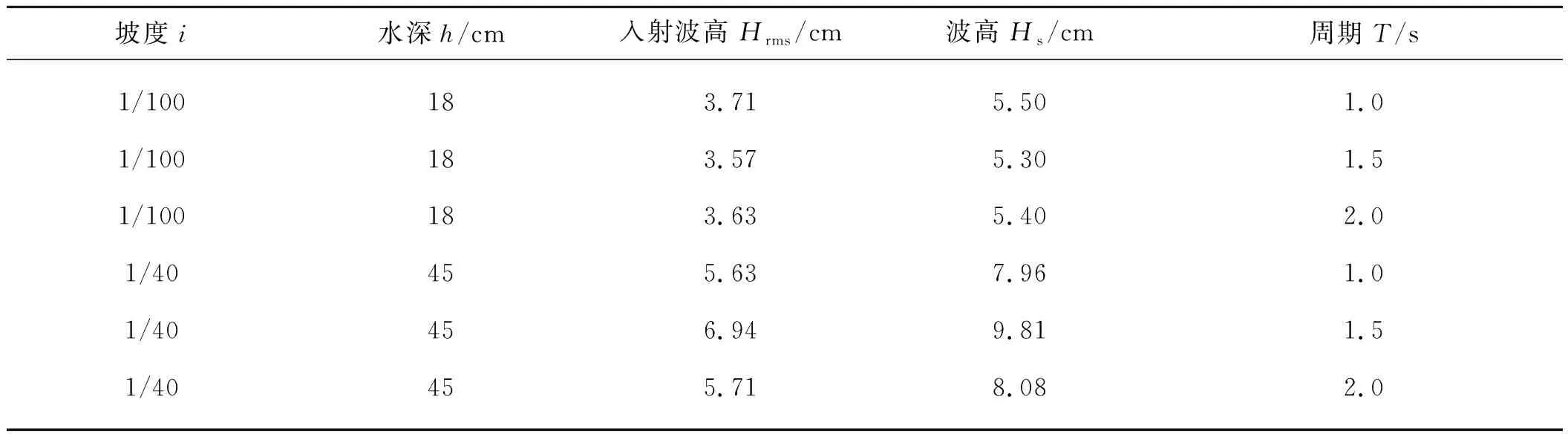
表1 试验条件Tab. 1 Experimental conditions

由于MIKE21 PMS模块适用于模拟大范围区域，这里将上述物理模型按长度比尺1∶100考虑，模拟其对应的原型海岸沿岸流情况。计算区域长10 km，宽3 km。结构化网格尺度为50 m×10 m，计算域共划分6万个网格。波浪摩擦系数cfw取为0.002；Thornton和Guza[11]的沿岸流数值模拟表明，涡流黏度对于不规则波浪作用下的沿岸流并无显著影响，模拟过程中涡流黏度系数取值为0.02。图1、图2为将数值模拟结果与物理模型试验结果的比较。数值计算所得的波高和流速沿程分布结果与试验数据吻合良好，并且破波点和最大流速出现的位置与试验结果基本一致。

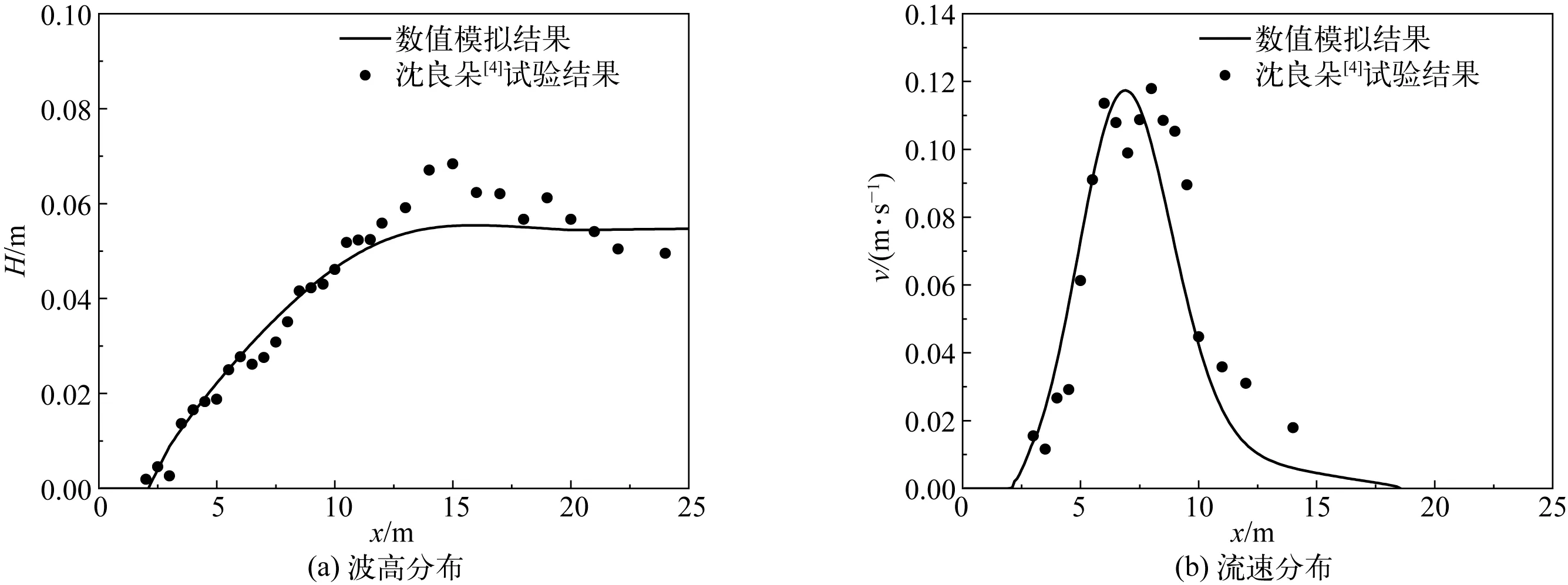
图1 波高与流速分布比较(i=1/100, Hs=5.30 cm, T=1.5 s)Fig. 1 Comparison of wave height and velocity distribution (i=1/100, Hs=5.30 cm, T=1.5 s)

图2 波高与流速分布比较(i=1/40, Hs=9.81 cm, T=1.5 s)Fig. 2 Comparison of wave height and velocity distribution (i=1/40, Hs=9.81 cm, T=1.5 s)

2 沿岸流流速分析方法

2.1 沿岸流流速无量纲化方法

为了便于工程应用，对沿岸流的数值模拟结果，采用如下的无量纲化[12]处理方法:

(4)

(5)

其中，V是无量纲流速，v是实际流速，H为有效波高，α为波浪入射角，X为无量纲距离，x为离开静水岸线的距离，L为谱峰值周期所对应的波长。

同时，这里选取H/L、H/h、sinα三个无量纲化参数作为流速的影响参数可用来代表入射波浪条件和地形条件。

2.2 沿岸流流速剖面函数拟合方法

经上述无量纲化处理后，流速V与离岸距离X之间可建立函数关系。

V=F(X)

(6)

其中，F选取高斯分布函数，其函数图像和函数表达式分别如图3和式(7)所示。

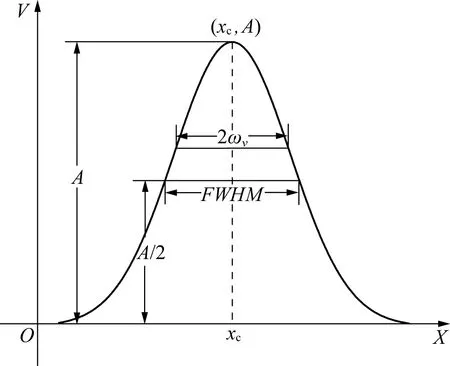
图3 Gauss分布函数Fig. 3 Gauss distribution function

(7)

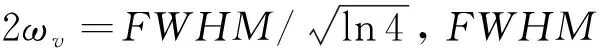
沿岸流速的最大值A与深水波浪要素和地形坡度皆有关，可设：

A=F3(H/h,H/L,sinα,i)

(8)

其中，F3为待定的拟合函数，h为深水区域平底处的水深，i为地形坡度。图4为岸坡坡度1/100时不同H/h条件下数值计算得到的无量纲沿岸流速最大值Vmax随H/L和α的变化情况。

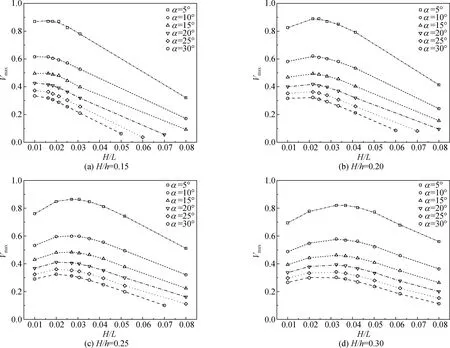
图4 无量纲沿岸流速最大值Vmax (i=1/100)Fig. 4 Dimensionless maximum current velocity Vmax (i=1/100)

图4中数据表明无量纲沿岸流速的最大值在每个波向下会存在一个峰值，以该峰值为分界点(M，N)，左右分别采用线性拟合，即可得到无量纲流速最大值A的表达式：

(9)

式中：假定K1(i)仅与坡度i有关，K2(i，H/h)、M(i，H/h)和N(i，H/h)均不随波浪入射角度改变而变化。求解K1、K2、M、N后即可确定流速最大值A。

房克照等[5]通过对5种入射角的波浪分别进行模拟，认为沿岸流速最大值的位置与波浪入射角度无关。可设：

xc=F1(H/h,H/L,i)

(10)

其中，F1为待定的拟合函数。

图5给出了坡度分别为1/100和1/40时无量纲沿岸流速最大值出现位置xc随H/L，H/h变化的数值计算结果。

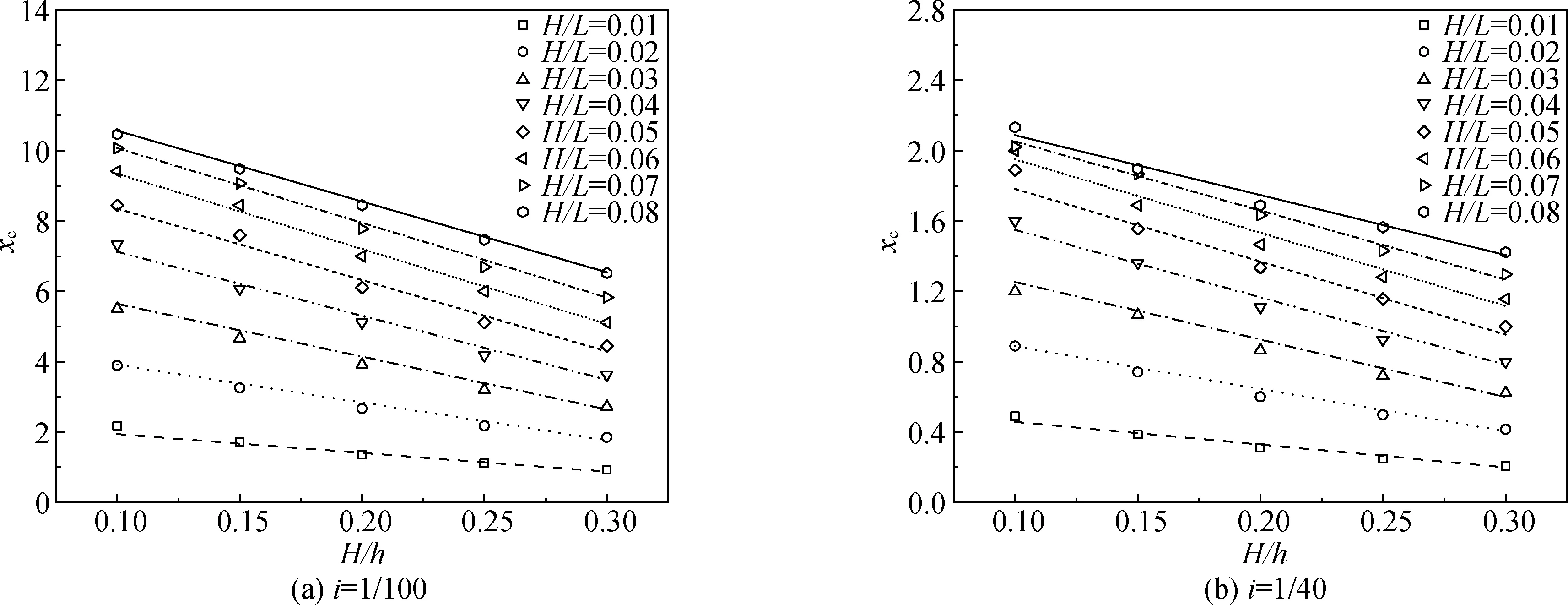
图5 无量纲沿岸流速最大值位置xc统计Fig. 5 Position of dimensionless maximum current velocity xc

图5中数据表明xc与H/h呈线性关系，可设：

xc=A1(H/L,i)+A2(H/L,i)·H/h

(11)

于是，求解A1，A2后即可确定流速最大值出现位置xc。

同样，沿岸流流速分布范围与波浪入射角无关，可设：

ωv=F2(H/h,H/L,i)

(12)

式中：F2为待定的拟合函数。

图6给出了坡度分别为1/100和1/40时，采用高斯分布函数拟合从而得到流速分布曲线中分布宽度ωv的值。

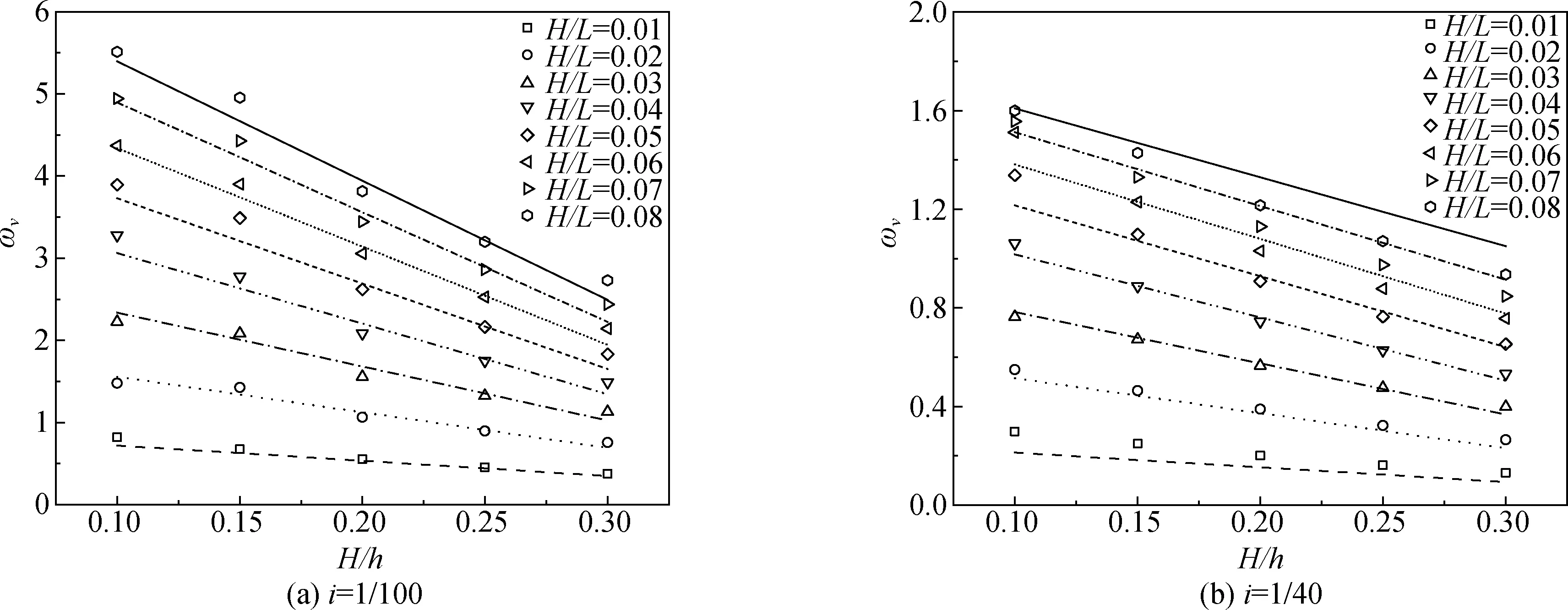
图6 沿岸流速分布宽度ωv统计Fig. 6 The value of ωv corresponding to the distribution curve of alongshore current velocity

类似的，ωv与H/h也呈线性关系，可设：

ωv=D1(H/L,i)+D2(H/L,i)·H/h

(13)

求解D1，D2后即可确定流速分布宽度ωv。

3 沿岸流流速分布函数

3.1 流速最大值A

对于流速最大值A的表达式，即式(9)，可采用Levenberg-Marquardt算法对数据点拟合得到以上4个待定函数的表达式：

(14)

K2=-15+500i-13 000i2+75 000i3+(23-200i)H/h

(15)

M=0.1H/h-0.03e-30i+0.02

(16)

(17)

无量纲化流速最大值A的拟合曲线与数值模拟结果的对比见图7。图中显示了在波浪入射角为10°时，不同岸坡坡度和不同H/h条件下沿岸流流速的最大值随着H/L的变化关系。随着坡度增加，无量纲沿岸流流速的最大值由0.65增大至3.00。

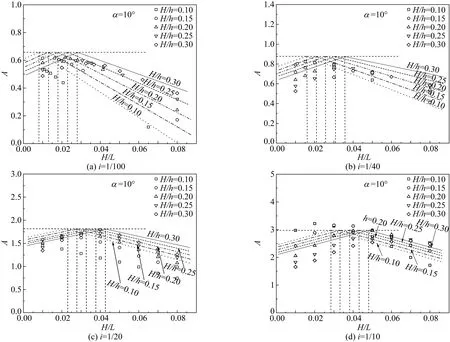
图7 流速最大值A的拟合曲线与数值模拟的数据点对比Fig. 7 Comparison between the fitting curve of the maximum velocity A and the data point of numerical simulation

3.2 最大流速出现位置xc

对于最大流速出现位置xc的表达式，即式(11)，可采用类似的算法分别对参数A1，A2与H/L进行二次函数拟合，设：

A1=B1(i)+B2(i)·H/L+B3(i)·(H/L)2

(18)

A2=C1(i)+C2(i)·H/L+C3(i)·(H/L)2

(19)

Bn和Cn(n=1,2,3)与坡度i进行拟合后可得到6个关于坡度i的函数：

(20)

(21)

图8给出了应用拟合公式计算出的xc与数值模拟数据对比。

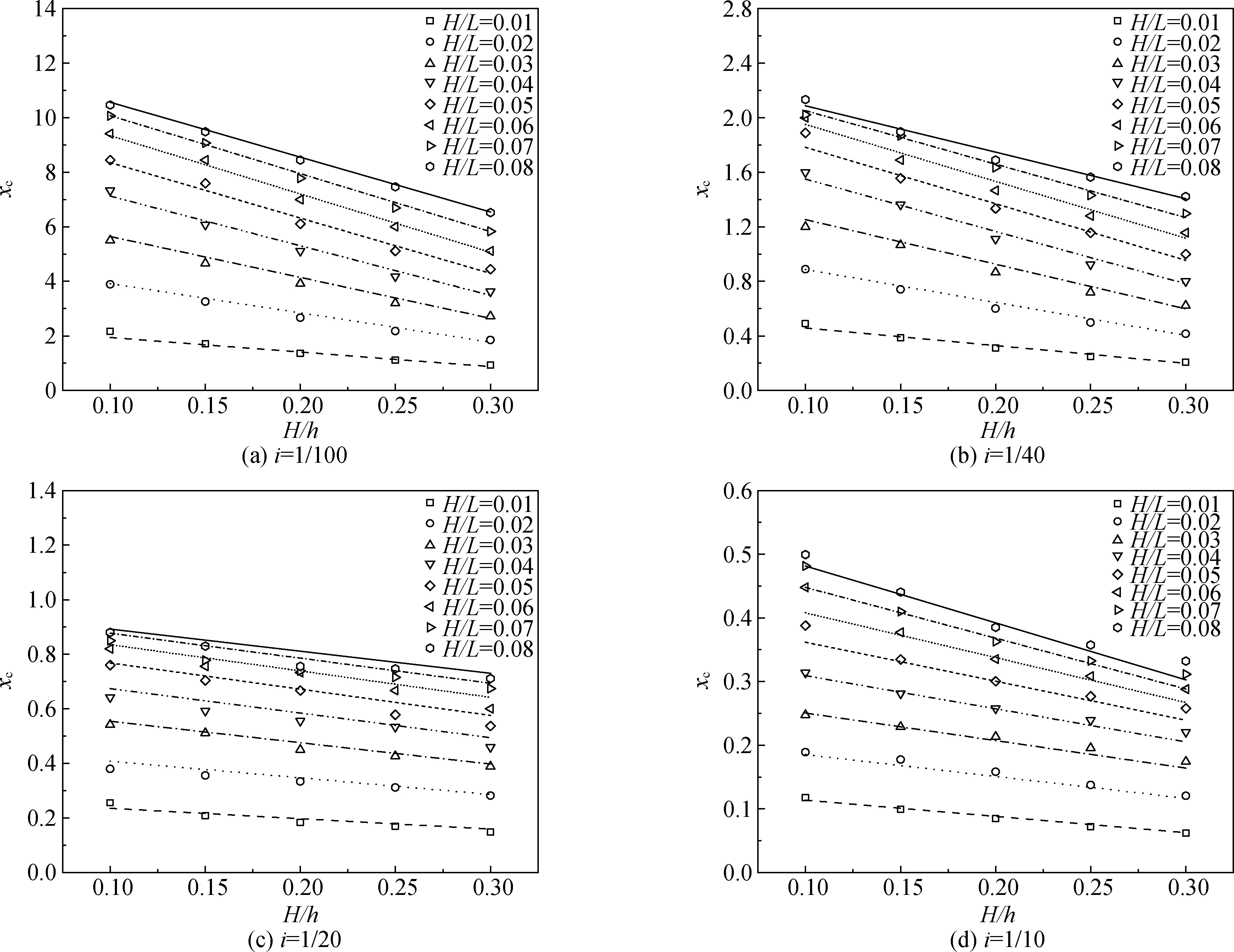
图8 流速最大值出现位置xc的拟合结果与数值模拟对比Fig. 8 Comparison of xc between fitting formula and numerical simulation

3.3 流速分布宽度ωv

同样，对于流速分布宽度ωv的表达式，即式(13)，将D1，D2与H/L进行二次函数拟合，可设：

D1=E1(i)+E2(i)·H/L+E3(i)·(H/L)2

(22)

D2=F1(i)+F2(i)·H/L+F3(i)·(H/L)2

(23)

En和Fn(n=1,2,3)与坡度i进行拟合可得到6个关于坡度i的函数：

(24)

(25)

图9给出的拟合计算得出的流速分布宽度ωv与数值模拟结果的对比表明，上述拟合公式可以近似表达出不同波浪入射条件和地形坡度下ωv的变化规律。

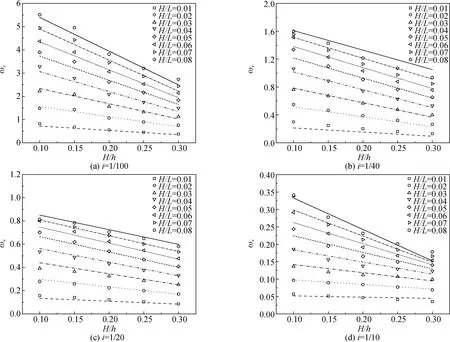
图9 流速分布宽度拟合结果与数值模拟对比Fig. 9 Comparison of ωv between fitting formula and numerical simulation

4 无量纲化沿岸流流速分布函数应用

4.1 流速分布函数验证

对应表1中另外4种波况，应用上述拟合公式可计算出沿岸流速分布公式的相应参数，进一步确定沿岸流的分布函数。图10为公式计算、数值模拟及物理模型试验得到的沿岸流速分布对比。图中数据表明拟合所得的沿岸流流速分布规律与物理模型实测数据较为吻合。

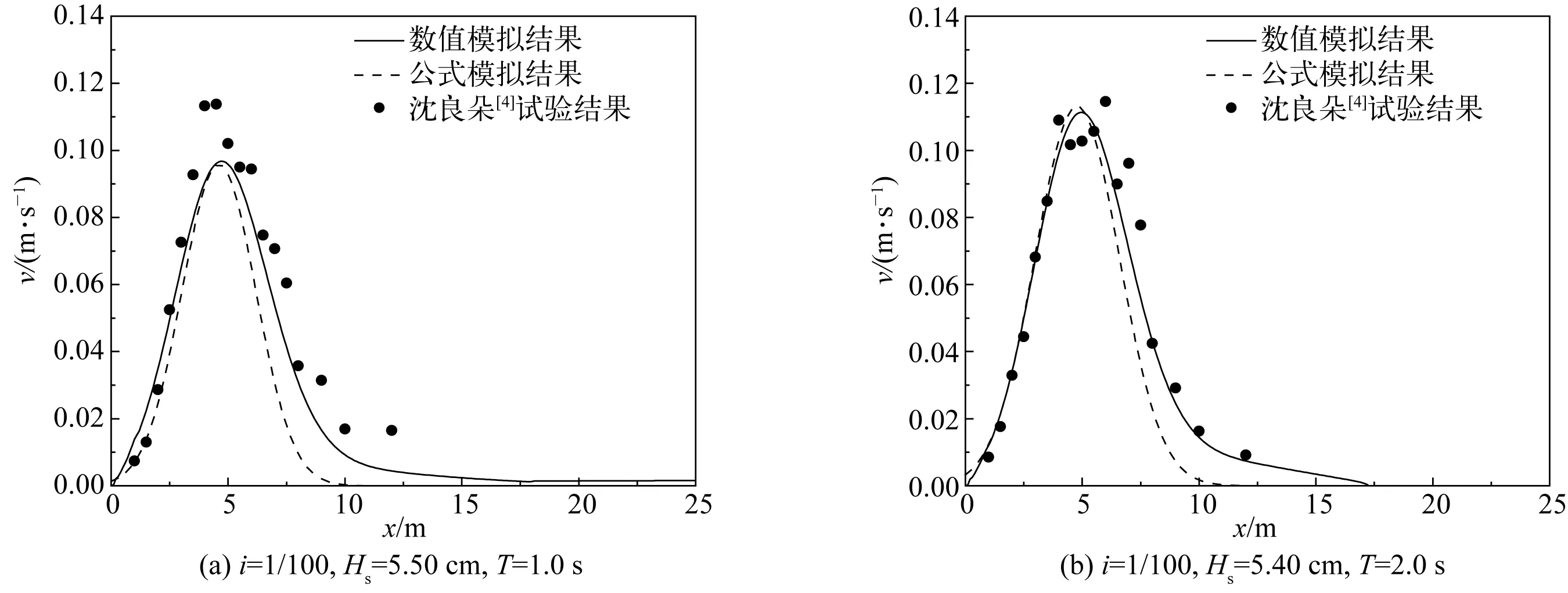
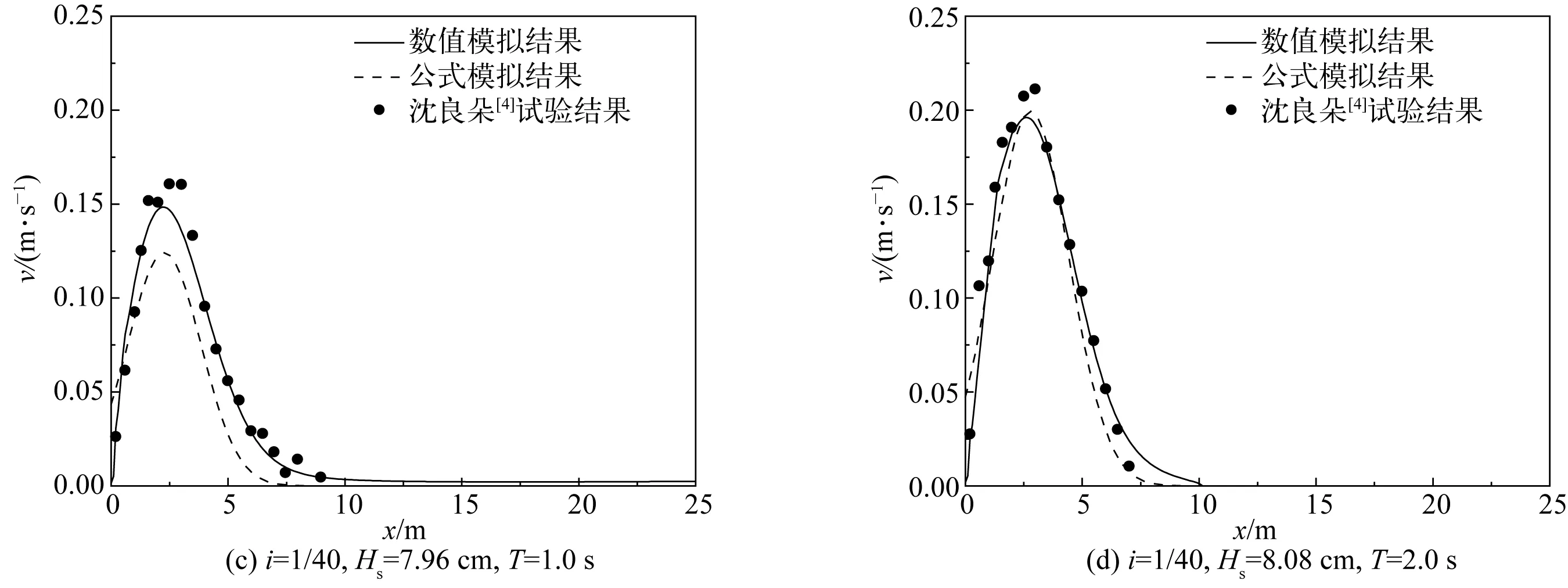
图10 拟合结果、数值模拟和模型试验的沿岸流流速分布对比Fig. 10 Comparison of current velocity distribution between formula calculation, numerical simulation and experiment

4.2 流速分布规律分析

上述分析表明无量纲沿岸流速分布与相对波高H/h、波陡H/L、岸坡坡度i以及入射波浪角度α相关。图11给出了不同相对波高H/h、波陡H/L、岸坡坡度i以及入射波浪角度α等参数条件下沿岸流流速分布规律的比较。

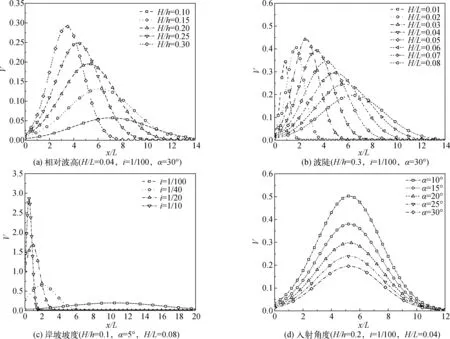
图11 无量纲流速分布规律对比Fig. 11 Comparison of dimensionless velocity distribution along with x/L

无量纲沿岸流流速的最大值受入射波浪的相对波高、岸坡坡度以及波浪入射角度影响显著，而受入射波浪波陡的影响相对较小。随着相对波高和岸坡坡度的增加，沿岸流流速最大值明显增大；而随着波浪入射角度的增大，无量纲化沿岸流流速最大值逐步减小。

无量纲沿岸流流速最大值的出现位置与入射波浪的相对波高、波陡以及岸坡坡度密切相关，但几乎不受波浪入射角度的影响。随着相对波高和岸坡坡度的增大，沿岸流流速最大值的出现位置逐步向静水岸线方向移动，而随着波陡的增大，逐步远离岸线。

流速分布宽度受入射波浪的相对波高、波陡以及岸坡坡度的影响显著，但不受波浪入射角度的影响。随着相对波高和岸坡坡度的增大，沿岸流的分布宽度明显变窄，沿岸流表现为向岸线方向集中；而随着波陡的增大，分布宽度逐步变广，即沿岸流的影响范围向着离开岸线的方向拓展。

5 结 语

对不同坡度地形下的波生沿岸流进行了数值模拟，并采用高斯分布函数对无量纲化的沿岸流流速剖面分布进行拟合，获得了无量纲沿岸流速最大值A与其出现位置xc以及流速剖面分布宽度ωv随着入射波浪条件和地形坡度的变化关系。

1)无量纲沿岸流的流速最大值与入射波浪条件和岸坡坡度密切相关。流速的最大值随着相对波高和岸坡坡度的增加显著增大，但随着波浪入射角度的增大而逐步减小。

2)沿岸流流速最大值所出现的位置与波浪的入射角度无关，但受入射波浪的相对波高、波陡和岸坡坡度的影响较大。相对波高和岸坡坡度变大，沿岸流流速的最大值所出现的位置均向着靠近岸线的方向移动。

3)沿岸流流速分布的剖面宽度与波浪的入射角度无关，在岸坡地形较陡时，沿岸流流速剖面分布较窄，且相对波高的增加会使得沿岸流的分布向岸线方向集中。