回转体并联入水运动状态预测

王 聪,何超杰,余德磊

(哈尔滨工业大学 航天学院,哈尔滨 150001)

在海上进行反水雷作战时，往往需要短时间内投放多枚射弹，使敌方防御系统短期内应接不暇.这是典型的运动体并联入水过程.该过程中，两个或多个运动体同时或在极短时间间隔内平行地穿越自由液面进入水中，由于各运动体流场和弹道存在耦合作用，力学环境更加复杂，运动体极易发生运动失稳.

国内外对单个运动体入水开展了大量的研究，包括空泡形态特性、运动体受载特性和弹道特性. Logvinovich[1]提出了空泡独立膨胀原理，为后续的空泡形态研究提供了理论基础；Lee等[2]提出了高速入水空泡形态发展的理论分析方法，该方法可以模拟高速入水过程中空泡的生成及溃灭；Aristoff等[3]基于空泡压力平衡理论和势流理论提出了空泡形态的理论求解方法；王京华等[4]基于空泡独立膨胀原理，研究了空泡的记忆效应及其对空泡形态的影响，详细计算了超空泡航行体各部分所受的流体动力，并提出了避免滑行力出现的预测和控制方法；张伟等[5]进行了不同速度、形状弹体入水试验，得到了3种弹体的入水初期空泡形态与运动特性，建立了平头运动体入水的空泡形态和弹道预测模型；王柏秋等[6]基于动网格技术对超空泡射弹的阻力系数开展了数值研究，结果表明同一模型长细比下，模型阻力系数随时间呈准线性变化；马庆鹏等[7]开展了不同速度下的锥头柱体高速入水过程数值研究，发现入水速度越高，航行体头部压力峰值越大，相同时刻入水空泡最大直径也越大；何乾坤等[8-14]对超空泡射弹的尾拍特性进行了大量数值研究.

目前国内外对并联入水的研究较少.卢佳兴等[15]基于高速摄像技术开展了圆柱体并联入水空泡演化特性的实验研究，发现各深度空泡截面扩张和空泡中心偏移的峰值和持续时间均随弗劳德数增大而先增后减；宋武超等[16]基于势流理论提出了回转体低速并联入水过程空泡形态发展的预测方法.综上所述，对入水问题的研究多针对单体入水，涉及并联入水的研究非常少，且未考虑空化现象对运动体并联入水流体和运动的影响.

本文基于对急动度的限制性假设，推导出描述圆柱体并联入水侧向位移和偏航角的预测公式，研究初始空化数和初始净距等初始条件对侧向和偏航运动特性的影响及其机理，提出避免回转体运动失稳的策略.

1 数值计算方法

1.1 控制方程及其求解

本文基于有限体积法对雷诺时均的N-S方程进行离散，使用VOF多相流模型描述各相分布. 混合介质的连续性方程为

(1)

其中i=1,2,3，下同. 动量方程为

(2)

式中：ρm=αlρl+αgρg+αvρv，μm=αlμl+αgμg+αvμv.αl、αg、αv分别为水、空气和水蒸气的体积分数；ρl、ρg、ρv为三相的密度；μl、μg、μv为三相的动力黏度；μt=ρmCμk2/ε为湍流黏性系数；Cμ为经验常数；k为湍动能；ε为湍动耗散率；ui、uj为速度分量；xi、xj为位移分量.Cμ由下式确定：

(3)

本文采用适用于大雷诺数流动的realizablek-ε模型[17]，其湍动能和湍动耗散率的输运方程分别为:

Gk+Gb-ρε-YM+Sk,

(4)

(5)

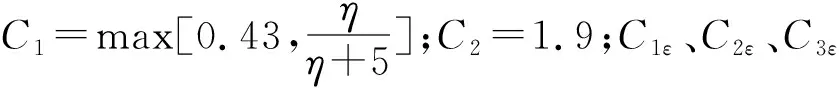
本文采用Schnerr and Sauer空化模型[18]描述空化现象.水蒸气相输运方程为

(6)

式中:RB=1×10-6m为气核半径；αnuc=5×10-4为不可凝结气体体积分数；p为远场压力；pv为饱和蒸气压；Fvap=50,Fcond=0.001.

1.2 方法有效性验证

文献[4]中给出了同实验结果符合良好的空泡形态模型，其表达式为

(7)

式中:R为空泡半径；R0为头部半径；z为位移；z0为初始位移；σ0、σ分别为初始空化数和空化数；Cd=C0(1+σ),0.82≤C0≤0.83；N为经验系数，取为2.

为验证计算方法的有效性，对半径5 mm的圆柱体以98.7 m/s入水过程进行数值计算，并和式(7)进行对比.由图1中可知两者较吻合，说明本文数值计算方法是可信的.

图1 空泡形态对比

2 侧向位移和偏航角预测公式

并联入水具有对称性，两回转体的侧向位移和偏航角大小相等，方向相反.本文约定质心相互远离的方向为侧向位移的正方向，头部远离而尾部靠近的旋转方向为偏航角的正方向，如图2所示. 图3给出了直径D=10 mm，长l=60 mm铝制圆柱体在初始空化数σ=0.02，初始净距d=0.6D条件下并联入水的侧向和偏航运动曲线. 由图2可以看出，由于头部靠近内侧的压力较大，回转体受到负方向偏航力矩，导致负方向偏航运动；偏航运动使头部压力对回转体产生正向附加侧力，引起正方向侧向位移.

图2 并联入水示意图

图3 左侧回转体侧向和偏航运动

进一步考察侧向加速度和偏航角加速度可知，入水初期两者波动性均较强，随着时间增加逐渐趋于线性变化.因此若忽略波幅较小的波动，可近似认为t较小时侧向加速度和偏航角加速度曲线均有4个极值点，而t充分大时两者为线性变化，如图4所示.因此由罗尔中值定理可知，侧向急动度和偏航角急动度在t较小时都至少有3个极值点，而当t充分大时两者都几乎为零.于是对侧向急动度和偏航角急动度作如下两个限制性假设：1)侧向急动度和偏航角急动度曲线均有3个极值点；2)侧向急动度和偏航角急动度在t充分大时均收敛于零.

图4 侧向加速度和偏航角加速度的波动性

据此设侧向急动度和偏航角急动度分别为:

(8)

式中：cXn、cθn为待定参数；fXn(t)、fθn(t)为待定的单调减函数，为使假设成立应满足:

tnfXn(∞)=0,tnfθn(∞)=0.

(9)

对式(8)积分，并注意到积分第二中值定理可得：

(10)

其中：FXn(t)、Fθn(t)由下式确定：

ξXn(t),ξθn(t)∈[0,t].

(11)

同样地，应用积分第二中值定理对式(10)连续积分两次得到侧向位移和偏航角分别为:

(12)

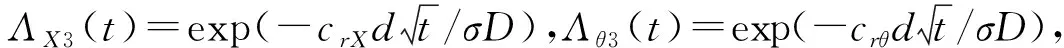
(13)

式中:cX、cθ分别为侧向和偏航角名义急动度；crX、crθ分别为侧向和偏航角修正因子.这些参数对于确定的并联入水过程是常数，而对于给定外形和材质的回转体则是初始空化数和初始净距的函数.

3 运动特性分析

取表1中各初始条件的数值仿真数据对式(13)进行拟合，如图5所示，拟合结果同式(13)吻合.

表1 初始条件

从图5还可以看出，同一时刻侧向位移和偏航角随初始空化数减小而增加，随初始净距增加而先增后减.结合图2对此解释如下：头部压力随初始空化数减小而增大，因此初始空化数越小，回转体所受偏航力矩和附加侧力越大，从而侧向位移和偏航角越大；速度驻点位置随初始净距变小而越靠近内侧，但初始净距较小时，速度驻点位置几乎不再向内侧偏移，故初始净距较大时，偏航力矩随初始净距减小而增大，使偏航角随初始净距减小而增大，进而使附加侧力随初始净距减小而增大，而初始净距较小时，内侧靠近尾部的低压区对回转体有正方向力矩，使偏航力矩和附加侧力随初始净距减小而减小，从而使侧向和偏航运动受到限制.

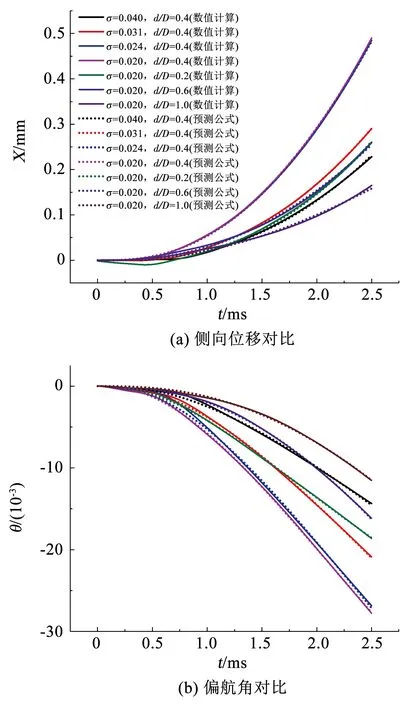
图5 预测公式与数值计算对比

为定量考察初始空化数和初始净距对侧向和偏航运动的影响机理，图6给出了名义急动度cX、cθ和修正因子crX、crθ随初始条件的变化.可以看出，cX和cθ随着σ减小而增大，而随d/D增大而先增后减；crX和crθ随d/D减小而增大.这进一步说明初始空化数越小，头部压力对侧向和偏航运动的促进作用越强，而初始净距越小，内侧低压对侧向和偏航运动的限制作用越强.

图6 不同初始条件下的名义急动度和修正因子

4 避免失稳的策略

侧向和偏航运动使回转体逐渐偏离平衡点，可能使回转体碰撞或过度远离，导致运动失稳.因此获得碰撞和过度远离的条件很有必要.

定义运动状态因数β为净距变化量与初始净距之比的相反数，即

(14)

回转体发生碰撞时，头部内侧与对称线接触，如图7所示.此时满足如下几何关系:

图7 回转体碰撞状态示意

(15)

亦即

(16)

上式即是碰撞状态的判据.本文约定|β|≤1，当且仅当β=1时回转体碰撞，当且仅当β=-1时为过度远离状态.式(14)可改写为

(17)

其中，λ为长细比，对于本文的回转体λ=24.

将式(13)代入式(17)即得β表达式.该式表明，运动状态不仅和初始条件(初始空化数和初始净距)有关，还同回转体的外形(长细比)相关.

图8比较了不同初始条件对β的影响.可以看出，对同一初始净距，存在使回转体最接近初始状态的初始空化数；对同一初始空化数，存在使回转体净距最接近初始状态的初始净距.而为避免运动失稳，应当力求|β|尽量小.因此对于已确定形状和材料的回转体，应控制入水初速度和初始净距在合理的范围内.对于本文的圆柱体，若初始净距为0.4D，则入水初速度应控制在79.64 m/s左右(对应于图8中σ=0.031,d/D=0.4)；若入水初速度为98.7 m/s，则初始净距应控制在0.4D～0.6D之间(对应于图8中σ=0.020,d/D=0.4及σ=0.020,d/D=0.6).

图8 β-t曲线

5 结 论

1)预测公式与数值计算结果符合良好，具有一定的可信度.

2)入水后同一时刻，运动体的侧向位移和偏航角均随初始空化数减小而增大，随初始净距减小而先增后减.

3)初始空化数较低时头部压力对侧向和偏航运动具有促进作用，且初始空化数越小，侧向名义急动度和偏航角名义急动度越大，表明侧向和偏航运动所受促进作用越强；初始净距较小时，内侧压力对侧向和偏航运动具有抑制作用，且初始净距越小，侧向修正因子和偏航角修正因子越大，表明侧向和偏航运动所受抑制作用越强

4)初始条件和回转体外形共同决定了并联入水过程中回转体的运动状态.对于本文运动体，当初始净距为0.4D，则入水初速度应控制在79.64 m/s左右；若入水初速度为98.7 m/s，则初始净距应控制在0.4D～0.6D之间.