基于Q学习算法的再生制动能量回收控制策略*

马什鹏 尹燕莉 张刘锋 马永娟 黄学江

（重庆交通大学机电与车辆工程学院）

目前，世界各大汽车企业都致力于开发电动汽车来实现节能减排，再生制动能量回收技术是电动汽车开发的关键技术之一[1-2]。再生制动研究的核心是在制动安全的前提下，合理分配机械摩擦制动力和电机制动力，即制动力分配控制策略[3-4]。为解决再生制动过程中制动力合理分配的问题，文章提出了基于Q学习算法的再生制动能量回收控制策略，以制动能量回收效率最大为优化目标，总需求制动力矩和车速为状态变量，运用Q学习算法，获得最优制动力分配系数，从而实现机械制动力和再生制动力的优化分配。

1 混合动力汽车模型

1.1 混合动力汽车结构参数

文章研究的混合动力汽车是一款前驱并联型轻度混合动力轿车，其主要部件包括发动机、电动机和无级变速器等，整车的主要参数如下：整备质量m=915 kg，轴距L=2.365 m，质心高度hg=0.525 m，质心离前轴的距离a=0.935 m，轮胎半径r=0.272 m，滚动阻力系数f=0.009，空气阻力系数Cd=0.335，迎风面积A=2.0 m2，主减速比4.38。

1.2 车轮处的制动需求力矩

在制动过程中，汽车主要受滚动阻力、空气阻力和车轮处制动力的作用。当制动踏板被踩下时，车轮处的制动需求力矩由制动器制动力矩和电机制动力矩来提供。

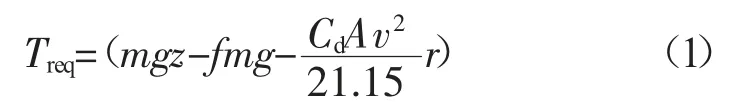
式中：Treq——车轮处的制动需求转矩，N·m；

v——车速，km/h；

z——制动强度，是加速度a与g的比值。

1.3 再生制动力矩

再生制动过程中，电机处于发电状态，再生制动力矩可以表示为：

式中：Tm——电机转矩，N·m；

i0——主减速器速比；

icvt——变速器速比；

ηt——传动效率。

2 基于Q学习算法的再生制动能量回收控制策略

2.1 制动力矩分配系数

文章引入了2个制动力分配系数，分别为前轴制动力矩比例系数和电机制动力矩比例系数。其中：前轴制动力矩比例系数为前轴制动力矩与总制动力矩的比值，电机制动力矩比例系数为电机制动力矩与前轴制动力矩的比值。

式中：Tf，Tr，Tre——前轴总的制动力矩、后轴总的制动力矩、电机制动力矩，N·m；

β——前轴制动力矩比例系数；

α——电机制动力矩比例系数。

2.2 目标函数和约束条件

以制动能量回收效率最大为优化目标，制定目标函数：

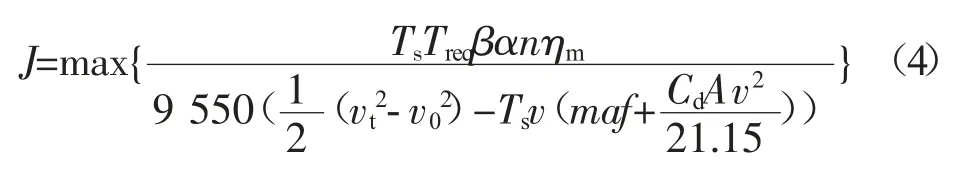
式中：Ts——制动时间，s；

n——电机转速，r/min；

vt，v0——制动起始车速和制动终止车速，km/h。

制动过程中为了确保制动安全性，前轴制动力矩比例系数要受到ECE法规的限制，电机制动力矩主要受电机本身特性和电池最大充电功率影响，故优化过程中的约束条件为：

式中：Tm_max——电机的最大转矩，N·m；

Pchg_max——电池最大充电功率，kW；

ηm——电机发电效率；

φf、φr——前轴、后轴的利用附着系数。

2.3 Q学习算法再生制动控制策略

Q学习算法是通过不断的试错学习经验知识，从而实现状态到动作的高维映射关系的自学习，通过不断地改善其行为从而达到良好的控制效果，最后得到全局最优策略[5-6]。把Q学习算法应用到再生制动的制动力矩分配上，以制动能量回收效率最大为优化目标函数，车轮处制动需求制动力矩和车速为状态，优化得到最优制动力矩分配系数。

图1示出文章所提控制策略的总体框架。首先，根据车辆状态获得车辆的车速、制动强度以及电池的SOC值，运用公式（1）计算得到需求制动力矩；其次，通过Q学习算法优化得到的结果，插值得到车辆的最优制动力分配系数；最后，计算出目标电机转矩Tm_tag和目标前后轴机械摩擦制动力矩Th_tag_i。

图1 基于Q学习算法的再生制动控制策略框架图

其中，Q学习算法具体优化步骤如下：

1）初始化Q学习算法参数，即探索率、学习率ζ和折扣因子γ，并设置迭代次数。

2）选择车轮处需求制动转矩Treq和车速v作为状态变量，α和β作为动作变量。

3）考虑制动能量回收效率，构建回报函数公式（6）。

4）根据构建的回报函数，应用ε-greedy策略寻找最大Q(s,a)值对应的动作，计算当前状态s和动作a的回报r和下一时刻状态s’。

5）迭代循环优化。基于greedy策略选择下一时刻动作a’，通过公式（8）更新当前状态动作的Q(s,a)值。

6）迭代循环结束。将收敛后的Q(s,a)值对应的策略作为最优策略。

3 仿真与分析

利用MATLAB/Simulink仿真平台，基于WLTP循环工况进行整车仿真。仿真工况如图2所示，该循环工况共1 800 s，最高车速131.3 km/h，最大制动强度0.153。

图2 WLTP循环工况

以车轮处需求制动力矩和车速作为状态，通过Q学习算法优化得到整个循环工况的前轴制动力矩分配系数和电机制动力矩分配系数，结果如图3和图4所示。

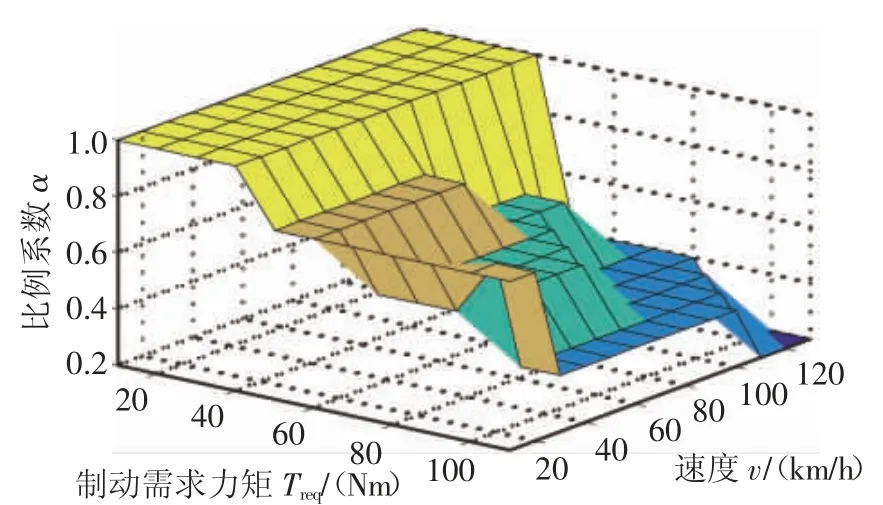
图3 电机制动力矩比例系数

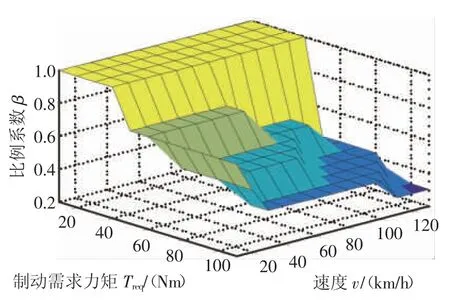
图4 前轴制动力矩比例系数

受整车比例阀控制前后制动器制动力为固定比例的影响，整个循环工况的电机制动力矩的比例系数和前轴制动力矩比例系数的变化趋势大致相同。图3电机制动力矩比例系数的最大值是1，此时是电机制动力矩等于前轴总的制动力矩，当车速一定时，随着电机比例系数随着需求转矩的增加而降低，表明当制动需求较大时，为了保证制动安全，会增加摩擦制动力矩，以保证制动安全性。图4为前轴制动力矩比例系数，其取值范围为0.6～1，符合ECE法规对于前轴制动力分配比例的限制，保证了制动安全性。当制动需求较小时，前轴单独提供制动力矩，前轴制动力矩比例系数为1；当制动需求转矩较大时，前轴制动力矩比例系数小于1，此时前轴和后轴共同提供制动需求。

如图5和图6所示，循环工况300～600 s的阶段里，电机的制动力矩较小，这是因为此阶段速度和制动强度都较低，整车需求制动力较小。在循环工况1 500～1 800 s的阶段里，电机制动力矩较之前阶段偏小，这是由于此阶段的速度较高，为了保证制动安全，减小电机制动力矩，增加机械摩擦制动力矩。

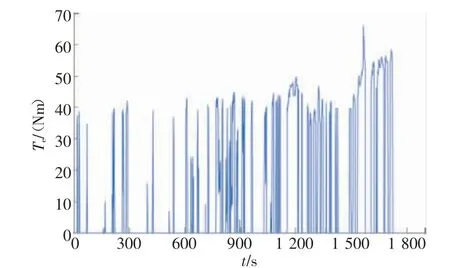
图5 发动机转矩

图6 电机转矩

图7示出WLTP循环工况下，采用基于Q学习算法再生制动能量回收控制策略，电池SOC随时间变化的情况，仿真循环初始时刻设定电池SOC为0.6。

图7 SOC变化图

从图7中可以看出，当电池SOC值上升时，电机参与制动，回收能量；当SOC下降时，表示电机驱动消耗电能，整个循环工况电池SOC值维持在0.598～0.603范围内。

表1示出文章所提控制策略和理想制动分配策略仿真结果的对比。由表2可以看出，基于Q学习算法控制策略的制动回收能量为1 845.6 kJ，总制动能量为3 212.2 kJ，整车能量消耗为7 048.9 kJ，制定能量回收效率为57.4%，有效制动能量回收效率为26.1%。其与理想制动力分配比例控制策略相比，能量回收效率提升了6.5%，有效制动能量回收效率提升了2.9%。

表1 两种控制策略仿真结果对比

4 结论

文章在混合动力汽车建模的基础上，在保证制动安全的前提下，以最大回收制动能量为目标，需求制动力矩和车速作为状态变量，制动力矩分配系数作为动作变量，制定了基于Q学习算法的再生制动能量回收控制策略，解决了再生制动过程中的电液制动力矩分配的问题。该方法不依赖于模型，通过不断的试错学习，从学习经验中改善自身性能，并且计算量小、运算速度较快。

最后基于MATLAB/Simulink仿真平台，进行了整车仿真试验。仿真试验结果表明，与理想制动力分配策略制动回收效率50.9%相比，该策略制动能量回收效率提高了6.5%。后期还需要对该策略的制动过程中的制动稳定性和电液制动系统的动态协调控制进一步研究。