主应力场驱动的复杂薄壁件刚度增强方法

张伟南 戴 宁 郭 策 余 逸 龚 赛

南京航空航天大学机电学院，南京，210016

0 引言

飞机机舱和导弹舱段等大尺度薄壁件在保留较高的结构完整性之外，还为机身和舱段内放置的其他物体预留大量的空间，承载效率很高[1]，但薄壁件的大跨度和小厚度导致刚度减小。复杂工况下，井字形加强筋在复杂薄壁件中的加强效果还有进一步优化的空间，所以需要一种新的方法来增大舱段这种复杂薄壁件的刚度。

目前实现复杂薄壁结构刚度增强的方法主要有两种：①使用高比刚度的材料，如钛合金和一些复合增强材料；②通过结构设计合理分配材料，如拓扑优化和近表面加筋法[2-3]，其中，拓扑优化又包括变厚度法[4-5]、变密度法[6]及微结构等效的均匀化方法[7]。

拓扑优化作为一种使用广泛的结构优化方法，将刚度最大的数学问题转化为材料的最优分布问题，但该方法在处理复杂薄壁结构的刚度增强问题时依旧存在局限性，难以用于薄板和杆的组合传力结构等其他组合传力结构。

近表面加筋法是工程中轻质高刚设计的一种方法，加强筋的布置主要依据工程师的经验[3]，比较常见的有“井字形”和“米字形”，但缺乏相关理论依据。自然环境中的生物体经过漫长的进化过程，具有适应恶劣环境的生物最优结构。通过前期调研，针对薄壁件刚度增强问题，笔者选择王莲作为研究对象，借鉴王莲叶片脉络的分布规律，对结构进行优化设计。

ZHANG等[8]、LI等[9]利用生物分支现象对机座结构壁板加强筋进行拓扑优化，提出一种提高比刚度的设计方法，但壁板很薄时，该方法对曲面形状加筋的优化效果不够明显。LI等[10]、KWOK等[11]提出基于主应力线的拓扑增长方法来解决材料最优分布问题，这种方法需要在初始结构生成时输入点载荷和约束的位置，对均布载荷的处理效果较差。WU等[12]受骨小梁启发，将基于主应力线方法生成的骨状多孔结构作为轻质填充料，通过增材制造的方法达到轻质高刚的目的，但缺点是内部空间被占用。LI等[2]提出一个基于主应力线的计算框架来设计和优化任意壳体上的肋板布局，提高了整体结构刚度和力学性能，该方法主要从计算机图形学的角度出发，结构刚度还有进一步增强的空间。文献[13-15]提出了沿主应力线进行增材制造的刚度增强方法，该方法涉及根据制造约束等因素对主应力线进行等效抽取的问题。

本文从仿生角度出发，借鉴王莲叶脉分布规律，提出等效主应力线计算模型并求解出体现整体密度的主应力线，沿等效主应力线对复杂薄壁件近表面进行加强筋的布局和优化，从而减小结构质量、提高结构刚度，有限元分析和物理试验验证了该方法的有效性。

1 基于主应力场的薄壁结构刚度增强

1.1 技术路线

基于主应力场的复杂薄壁结构刚度增强方法主要包含两个过程：①近表面有效主应力线生成；②加强筋优化设计。如图1所示，首先给定复杂薄壁结构，通过施加相应的边界条件生成主应力场(图1a)；之后，从应力场中提取相应的主应力线族，对主应力线族进行聚类操作，根据拓扑张量理论抽取等效主应力线(图1b)，同时，通过尺寸优化来调节加强筋的尺寸；最后使用增材制造的方式打印高刚优化模型(图1c)，并进行相关的物理测试。

(a)输入复杂薄壁件边界条件 (b)生成并抽取等效主应力线 (c)优化模型、金属打印并进行测试

1.2 高刚度结构仿生理论研究

自然界中的生物体可生长出适合恶劣环境的最优结构。对于薄壁结构的刚度增强问题，通过前期调查[16]，笔者选择王莲为研究对象，通过观察王莲叶片底部的筋脉分布对王莲进行建模，施加自然界中常见的水压和自身重力，在叶片中心的根部建立固定支撑，模拟王莲叶片在自然界中的承载并进行应力场分析，如图2所示。

(a)王莲生物学模型

王莲底部分布着纵横交错的筋脉，靠近根部的筋脉更加粗壮，筋更高、壁更厚，模型环向的主应力为拉应力，如图3所示，靠近根部的最大拉应力约为叶面边缘最大拉应力的7倍。

图3 王莲应力大小分布图

王莲环向的筋脉分布与主应力场的环向拉应力分布一致。王莲的筋脉从中心向四周发散，沿所受载荷而产生的最大主应力的轨迹分布，这与主应力场的径向压应力分布一致。笔者受此启发，沿薄壁结构近表面的最大主应力方向进行加强筋的布置，同时借鉴王莲筋脉的生物特征，对加强筋的尺寸进行优化，增大结构刚度。

1.3 主应力线的计算

在对主应力线进行描述之前，先对应力张量和应力张量场进行说明。应力张量为某点处的二阶实对称张量：

(1)

式中，σx、σy分别为X和Y方向的主应力；τxy为平行于XY平面的切应力。

将坐标系统绕原点逆时针旋转θ，则应力张量σ变换成

(2)

(3)

其中，Q为旋转矩阵；σ1、σ2为坐标系旋转过程中切应力为0时的应力张量σ的主应力。

在待求解空间区域中，定义位置点与应力张量关系的函数,即应力场函数为

(4)

要求解式(2)中的σ1和σ2，需要对相应位置点处的应力张量乘以旋转矩阵Q，使求解空间区域内相应的τxy(m,n)为0，即

(5)

式中，σ′(m,n)为经过张量转换之后的新的应力张量；σ1(m,n)、σ2(m,n)分别为该点处的第一(最大)主应力和第二(最小)主应力。

复杂薄壁结构的刚度优化是力流传递路径的优化，而主应力线提供了施加载荷后的力流方向，使结构受力路径可视化，揭示了材料连续分布的最佳拓扑结构，所以沿主应力线进行加强筋的布置能增大结构的刚度。为更好地将主应力线应用到结构设计中，在长40 mm、宽20 mm、厚1 mm的区域探究不同的种子点、载荷类型、载荷位置和约束类型对主应力线的影响。

LI等[10]在对变形体的研究中发现种子点影响主应力线的生成，选取的种子点不同，结构主应力线生成的稠密程度也不同，如图4、图5所示。

(a)种子点 (b)主应力线族

(a)种子点 (b)主应力线族

对模型添加不同的边界条件，发现不同的加载方式和约束方式对主应力线的生成影响很大。保持约束方式不变，将100 N的均布载荷变成模型上端中间位置的点载荷，生成的主应力线分布如图6所示；图7所示为将底部的线约束变成点约束的主应力线；图8为改变约束位置主应力线生成图，其中，红线为第一主应力线，绿线为第二主应力线，下同。

(a)顶部均布载荷 (b)顶部集中力载荷

(a)底部线约束 (b)底部点约束

(a)底部中右边约束 (b)底部两端约束

主应力线生成方式的研究很多[17]。如图9所示，本文首先给定复杂薄壁结构，通过在结构外侧施加均布气动载荷和在底部固定线约束进行有限元分析，沿结构近表面的种子点生成主应力场。然后获取设计域内生成主应力场的应力，根据应力提取节点处应力信息(应力的方向和大小)并存储。初始点P0处主应力σ1的方向向量为v0，沿该向量方向延长步长Δ，得到节点P1处的应力信息，重复获得节点的步骤，直到到达设计边界，经过所有节点的光滑曲线就是最终的主应力线[17]。

(a)节点处应力信息 (b)主应力线 (c)光滑曲线

节点之外的任意点处主应力线的方向和大小的确定。本文采用线性插值的方式，继续对设计域内的剩余种子点进行迭代处理，从种子点出发，生成若干主应力线族，如图10所示，图中，载荷为结构外侧施加的均布气动载荷，约束为结构底部施加的固定线约束。对图10所示薄壁结构进行有限元分析时，选择近表面的种子点生成主应力场。

图10 应力场中提取主应力线

1.4 等效主应力线模型的抽取

由图10可知，设计域内沿种子点生成了大量的主应力线，沿每根主应力线布置加强筋显然不现实，所以本文对主应力线族进行简化，获得等效主应力线计算模型[13]，如图11所示。首先按照每根主应力线的最大曲率对主应力线族进行聚类；接着对每一类主应力线进行迭代循环，保留Dmax≥ndk/mi的主应力线，继续进行下一次迭代。其中，dk为相邻两条主应力线之间最大曲率处的距离，mi为主应力线数量，n为用来调控结构表面加强筋的数量，由结构整体质量决定。本文除考虑制造约束外，还从拓扑张量理论出发，增加了“优势密集区域主应力线”，兼顾了每个主应力线族中主应力线的数量。具体算法如下：

图11 抽取出的有效主应力线

(1)导入主应力线族，计算第i根主应力线轮廓的最大曲率ki,max，将ki,max±Δk(Δk为根据聚类的族的数量设定的最大曲率的增减量)之间的主应力线聚为一族，将每一族中曲线按曲率大小排列成曲线集C={C0，C1，…}，其中，Ci为第i根曲线，i=0，1，2，…。

(2)使用距离求解函数Dmax计算每一族边界的相邻两条主应力线之间最大曲率处的距离dk和主应力线数量mi，求得该族主应力线密度dk/mi。

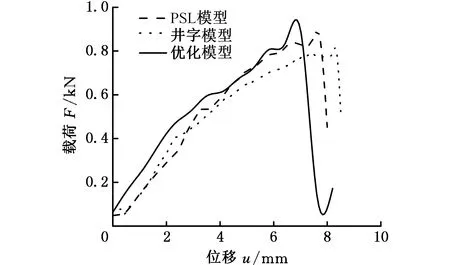
(3)求每一族的起始主应力线与下一条主应力线之间的最大曲率处的距离，如果Dmax

1.5 高刚结构近表面加筋优化

从主应力线族中抽取出等效主应力线后，首先进行曲线拟合，获得较高质量的线条，之后沿着拟合曲线在薄壁件内表面进行加强筋的布置，如图12所示。

图12 仿生高刚结构参数化建模

本文采用Screening优化算法建立优化设计模型。首先抽取对最大变形D有影响的壳体厚度T、加强筋宽度W和加强筋高度H，将T、W和H作为优化设计变量，添加初始值并设置取值区间，将结构最大变形D的最小值作为优化目标。考虑到曲面曲率及实际工况，设置合理的变量取值范围，求得各组候选迭代点的最大变形D并排序，选择最大变形D较小的解。约束条件为结构最大应力σ不超过材料的许用拉应力σt和许用压应力σc。求得最优解后，将尺寸用于结构设计，壳体厚度、加强筋宽度和加强筋高度对最大变形D的影响如图13所示。

(a)加强筋高度与壳体厚度

图13a所示为加强筋宽度不变时，加强筋高度和壳体厚度对最大变形的影响：壳体厚度对最大变形的影响较大，且对最大变形的影响呈负相关分布；加强筋高度对最大变形的影响较小。图13b所示为壳体厚度不变时，加强筋高度和宽度对最大变形的影响规律：加强筋高度对最大变形的影响较小。图13c所示为加强筋高度不变时，加强筋宽度和壳体厚度对最大变形的影响：加强筋宽度对最大变形的影响较小。由此可见，在求得最大变形D最小值的过程中，加强筋的宽度和高度与壳体厚度相互影响。对照组中，井字形结构的质量为538 g，优化方案1的质量为422.2 g，优化方案2的质量为404.8 g；优化方案3的结构质量为516.9 g，与对照组结构质量接近，变形量在优化方案中最小，所以选择第三组优化方案数据为后续的结构尺寸数据。三组最优解如表1所示。

表1 优化出的三组候选参数

2 实验验证与分析

2.1 薄壁结构刚度评价标准

综合考虑刚度、材料及结构质量等因素，引入比刚度结构效能δ来衡量刚度，δ越大，结构刚度越高大。δ的计算式为[13]

δ=E/(Dm)

(6)

式中，E为材料的弹性模量；m为结构的质量。

2.2 有限元分析

在有限元分析软件中进行仿真，设置材料的弹性模量为200 GPa，泊松比为0.3，密度为7.85 g/cm3。对照组使用井字形加强筋模型，实验组选择沿主应力线布置加强筋的主应力线(principal stress line，PSL)模型和优化尺寸后的模型。优化组尺寸为宽度1.73 mm，高度2.46 mm，厚度1.97 mm。3个模型的质量基本相同，使用同种材料，添加相同的边界条件和载荷，划分相同的网格，实验得到的参数指标如表2所示。

表2 三组结构尺寸

根据图14～图16所示的有限元分析结果得到实验数据，如表3所示，PSL模型的比刚度较井字模型大20%，优化模型的比刚度较井字模型大40.9%；优化模型的总应变能[19]比另外两种模型的总应变能小，侧面印证本文方法的可行性。

表3 各组模型实验参数

(a)应变云图 (b)应变能云图

(a)应变云图 (b)应变能云图

(a)应变云图 (b)应变能云图

2.3 物理压缩试验

对光固化技术打印的3种模型(图17)进行压缩试验。工件外表面为异形结构，很难通过机械压的方式添加气动载荷；通过液压或气压的方式添加均布载荷需要将工件上下封口，这种方式会改变异形结构本身的特点，失去了研究的意义，

(a)井字形 (b)PSL型 (c)优化型

所以我们使用等效的简化加载方式，如图18所示。

(a)井字模型 (b)PSL模型 (c)优化型模

对工件压缩后的相关数据进行整理，如图19所示，井字模型在最大载荷800 N、位移8.5 mm时出现明显的卸载，最大压缩刚度[20]为94 N/mm；PSL模型在最大载荷870 N、位移7.7 mm时出现明显卸载，最大压缩刚度为112 N/mm；优化模型在最大载荷910 N、位移7.6 mm时出现明显卸载，最大承载能力为900 N，压缩刚度为120 N/mm。

图19 三种结构的位移-载荷图

优化模型借鉴王莲叶脉的分布规律，材料沿着结构最大主应力方向分布；井字模型材料主要靠经验进行布置。由表4的数据可以看出，井字模型比刚度为174.72，优化模型比刚度为232.56，优化模型具有较大的比刚度；井字模型质量为538 g，优化模型质量为516 g，这说明优化模型的近表面高刚仿生结构对刚度提升效果明显。物理试验结果与有限元分析结果基本相同，表明使用本文方法设计的高刚仿生模型对比刚度的提升效果明显。

表4 各组模型的压缩刚度

3 结论

(1)本文基于仿生理论，提出复杂薄壁件刚度的复增强技术，物理测试结果表明，采用该技术设计出的薄壁结构比刚度较井字加强筋的薄壁结构比刚度大33%。

(2)有效主应力线计算模型考虑了拓扑张量、制造约束等因素，更符合结构优化常识。

(3)本文方法考虑结构具体的使用环境，所得近表面加强筋的分布具有较好的刚度提升效果。